基于新型標準數字功率源的數字化電能表檢定和溯源方法
宋曉林,任偉,邵方靜,謝靜,曾翔君
(1. 國網陜西省電力公司電力科學研究院,西安 710100; 2.西安交通大學,西安 710048;)
0 引 言
數字化電能表是應用于數字化智能變電站的計量裝置,與傳統模擬式電能表不同,其輸入信號為符合IEC 61850協議標準的數字報文[1-2]。因此數字化電能表的溯源和檢定方式法與傳統模擬電能表不同[3]。黑龍江省電力科學研究院針對這一問題提出了一種數字電能計量系統整體校驗法如圖1所示,傳統標準電能表校驗儀直接對標準電流互感器和標準電壓互感器輸出的二次信號進行采樣計算,得出標準電能值。然后通過與數字電能表發送的電能脈沖進行比較得到數字電能系統的電能計量誤差。該方法實現了數字電能計量系統(包含電子式互感器、合并單元、數字化電能表等)的檢定,但未解決對數字化電能表單獨進行量值溯源和檢定的難題[4]。
目前國內某單位針對數字化電能表的溯源與檢定提出了兩種方法[2]:
方法一:標準數字電能表比較法的框圖如圖2所示。在該方法中,將符合IEC 61850協議標準的數據幀同時輸入標準數字電能表和被檢數字電能表,然后直接比較電能計量結果得到被檢表的誤差。這種檢定方法的優點是操作簡便,但是該方法中的標準數字電能表本身的溯源尚未解決,這又回到了溯源方法的問題[5]。
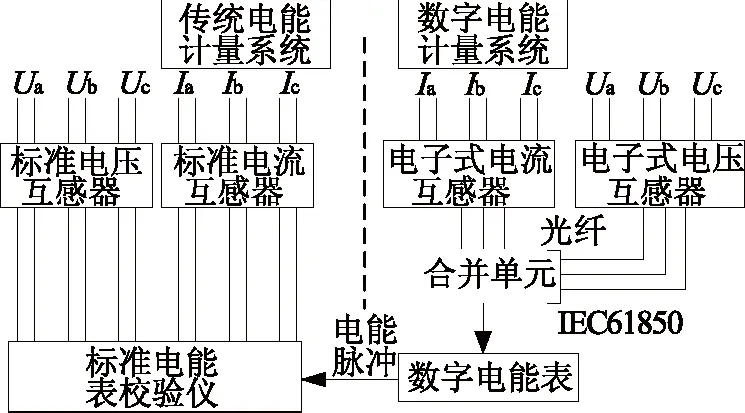
圖1 數字電能計量系統整體校驗法
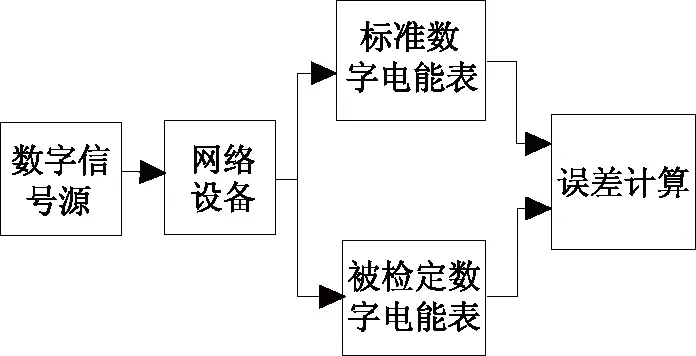
圖2 標準數字電能表比較法
方法二:標準數字功率源法的框圖如圖3所示。在該方法中,標準數字功率源輸出符合IEC 61850協議標準的數據幀,并且該數據幀所代表的電壓、電流信號的幅值和相位可以根據實際要求設置。根據標準數字功率源的的參數得到理論電能值,與被測表的計量結果比較就可以得到被檢表的誤差。該檢定方法的優點是結構簡單,但是由于數字功率源的輸出并非真正的電信號,不具備電能標準特性,不能直接向上溯源,該方法受到了業界人士的質疑[6-7]。

圖3 標準數字功率源法
數字化電能表實際上處理的是沒有量綱的數值,因此可以通過圖3給出的方法對數字化電能表單獨進行溯源和檢定,但不是量值溯源,而只是數值溯源。另外,這種傳統數字功率源輸出的是基于標準正弦波的數據,忽略了實際測量系統中由截斷誤差、模擬噪聲和諧波功率造成的不確定度。本文首先論述了數字化電能表數值溯源方法的理論據;進而針對傳統標準源法在實際應用中存在的問題給出了詳細的描述;最后提出了一種新型的標準數字功率源法,可以有效地解決數字化電能表的檢定和溯源問題。
1 數字化電能表的數值溯源及傳統標準數字源法存在的問題
數字化變電站計量系統的結構如圖4所示[8-9],電子式互感器將一次電壓和電流通過光學或其它方式傳感后轉換為數字量,即把模擬信號采樣離散化成數字序列(A/D轉換),然后對數字序列進行數字信號處理,得到輸出序列。

圖4 數字化變電站計量系統的結構示意圖
其中,A/D轉換過程的輸入—輸出關系式為:
最后得到:
(1)
式中D為A/D轉換結果;udn為量化噪聲以及模擬噪聲對應的模擬量;d為量化噪聲以及模擬噪聲對應的數字量。Ui為輸入電壓,N為轉換位數,Uref為參考電壓。由式(1)知,A/D轉換過程的輸出是一個沒有單位的數字量,所以A/D轉換之后都不存在量的溯源問題。由量化噪聲和模擬噪聲產生的誤差將以數字量d的形式傳遞到數字化電能計量系統中去。
合并單元采用一個標準的時鐘源作為輸入,并對采樣的數據進行匯總。從合并單元輸出的數字序列通過通訊系統傳送給數字化電能表。數字化電能表的實質是數值處理,只接收沒有量的數值。因此數字化電能表的溯源分為數值溯源和量的溯源兩個部分。因為在整個計量系統中始終存在誤差傳遞,例如模擬電路產生的噪聲、電力系統中的諧波都會轉換成數字量傳遞給數字化電能表進而影響電能計量的準確度,所以應對數字化電能表單獨進行數值溯源。若要進行物理量溯源,則必須對數字電能計量系統的整體(包含電子式互感器、合并單元、數字化電能表等)進行溯源,只要實現了參考電壓Uref的量的溯源就實現了數字電能計量系統的量的溯源。
數字化電能表實際上處理的是沒有量綱的數值,因此可以通過標準數字功率源法對數字化電能表單獨進行數值溯源和檢定。傳統標準數字功率源輸出的信號是基于標準正弦信號產生的數據幀,具有周期重復性,不具有A類不確定度。這種做法忽略了實際測量系統中由截斷誤差、模擬噪聲和諧波功率造成的不確定度,無法模擬實際測量系統中的不確定性。
另外,由于數字功率源數值精度的限制,理論功率值本身具有B類不確定度。一旦設定了標準數字功率源輸出的數據幀所代表的電壓、電流信號的幅值、相位和頻率,相應的功率理論值就是一個精確的定值。這就使得制造商有機會通過調整被檢表的算法對電能計量結果進行適當的修正,使其與理論電能值完全一致,從而掩蓋了電能表本身的算法誤差。看似B類不確定度得到了修正,但在實際測試環境中由于各種影響量的引入,被檢表的測量準確度將有不同程度的下降。所以基于標準正弦波的數字功率源檢定法存在不嚴謹之處。
2 基于新型標準數字功率源的檢定方法
2.1 檢定方案概述
針對數字化電能表的檢定,本文提出了一種基于新型標準數字功率源的檢定方案如圖5所示。根據標準數字化電能表只有數值溯源而不存在物理量的溯源以及理論值即真值的觀點,將三角函數形式的傅立葉級數與隨機函數相加所得的復合函數作為新型標準數字功率源的輸出形式,這就可以通過調節隨機函數的參數來改變數字功率源的B類不確定度。
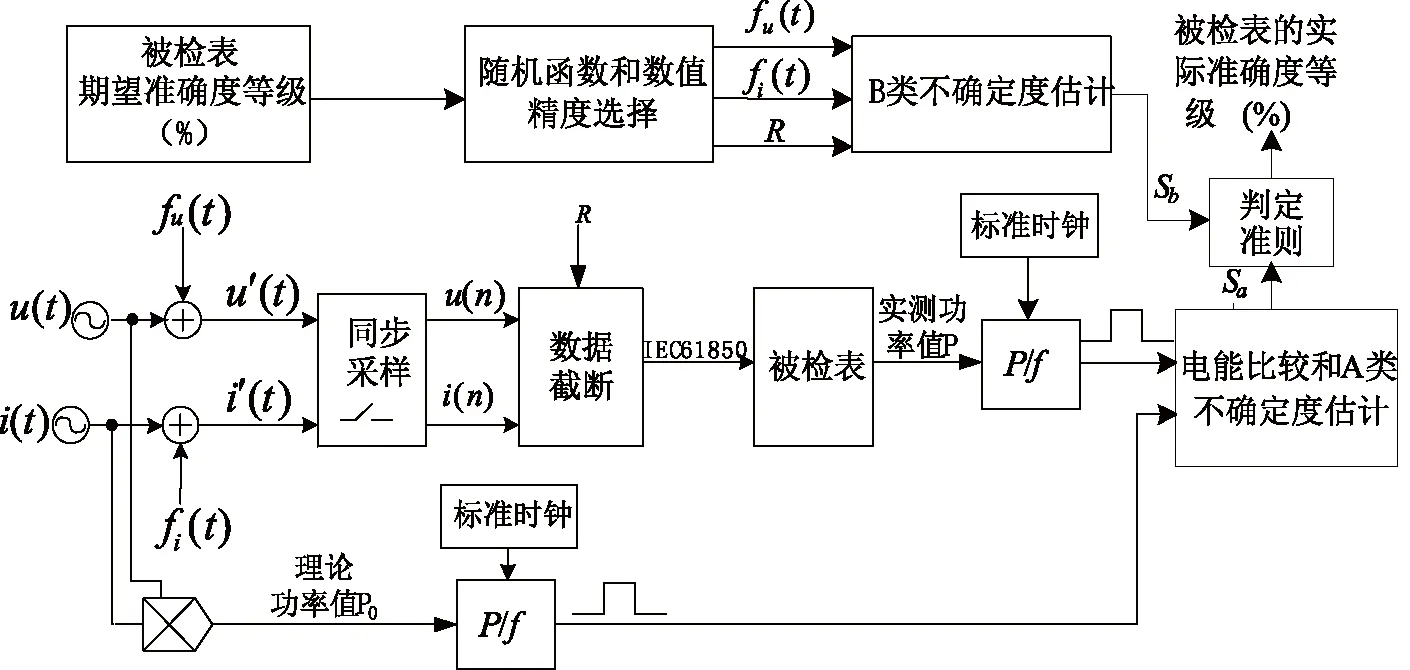
圖5 推薦的檢定方案
具體檢定步驟如下:
(1)在給定標準數字功率源的理論功率P0的情況下,根據被檢數字化電能表的期望準確度等級來確定數值精度R和隨機函數fu(t)、fi(t)的參數;
(2)由標準數字功率源產生傅里葉級數形式的三角函數u(t)和i(t),分別與隨機函數fu(t)、fi(t)相加得到復合函數u′(t)和i′(t);把u′(t)和i′(t)送入同步采樣模塊,再經過數據截斷得到離散值u′(n) 和I′(n);同時,數據截斷和隨機函數的引入使測量結果產生B類不確定度Sb;
其中,u′(t)和i′(t)的表達式為:
(2)
式中角頻率ω、初相位φu和φi均可調;φu和φi要保持恒定的相位差,即φu-φi=Ф;Un和In為電壓、電流的n次諧波幅值;理論功率值P0的表達式為:
P0(t)=u(t)×i(t)
(3)
(3)基于IEC 61850通信協議把離散值u′(n)和i′(n)發送給被檢數字化電能表;
(4)將被檢數字化電能表輸出的實測功率值P和理論功率值P0同時送入P/f模塊,通過電能比較得到被檢數字化電能表的A類不確定度,根據合成不確定度判定被檢數字化電能表的實際準確度等級。
2.2 數值精度的選擇和檢定規則
數據截斷會引起截斷誤差并傳遞給被檢表的測量結果,產生B類不確定度對測量準確度造成影響。即使計算方法準確,也不能得到真值,所以對不同等級表檢定時必須對數值精度進行規定。輸入數字表的數值精度取決于A/D采樣精度和數據存儲位數,與被檢表自身的準確度無關。
截斷誤差類似AD轉換過程中產生的量化誤差。截斷誤差的分布是一個周期鋸齒波如圖6所示。

圖6 截斷誤差分布
其幅度范圍是[-Δ/2,+Δ/2],Δ=1/2N,N為數據存儲的位數。截斷誤差f(x)的復指數傅立葉級數為:
(4)
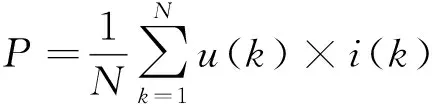

表1 不同數值精度數據引起的擴展不確定度
所以對不同準確度等級的數字表檢定時應該采用不同數值精度的數字源,選擇的依據見表2。校驗步驟分為2步。
步驟1:嚴格按照表2的規則選擇數值精度足夠的標準數字功率源作為被檢數字化電能表的輸入,評估被檢數字化電能表的測量不確定度。例如,對期望準確度等級為0.02級的數字化電能表定級時,只能選擇32位、24位或16位數值精度的數字化功率源作為被檢數字化電能表的輸入。若被檢數字化電能表的測量結果相對真值的不確定度S≤0.02%,則進行步驟2校驗;否則認為不能達到期望的準確度等級。
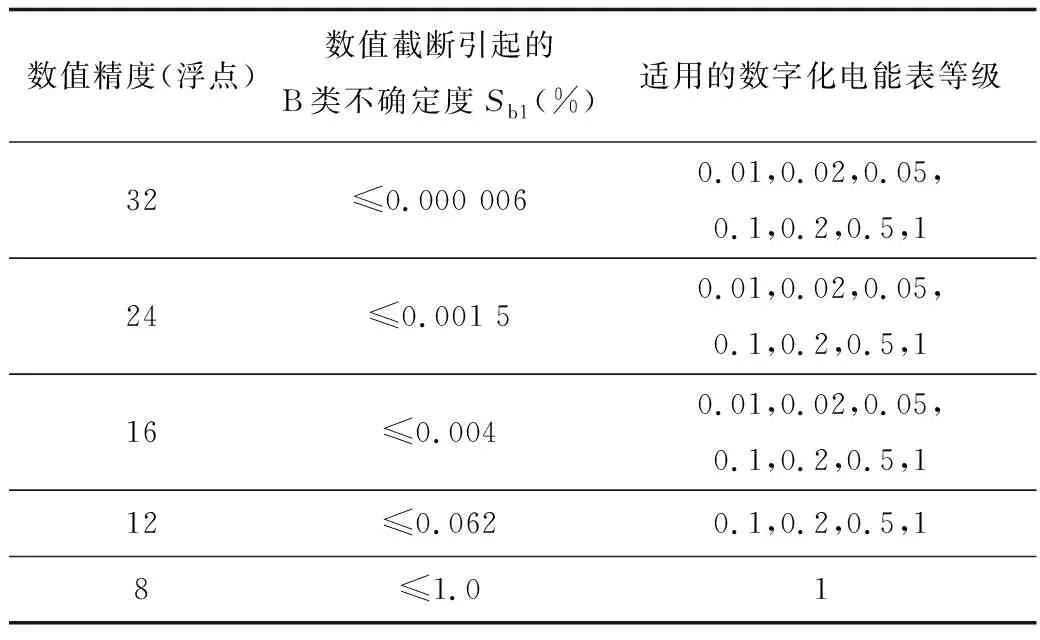
表2 數字源數值精度的選擇依據
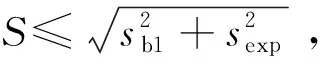
經過上述2步校驗,滿足條件的被檢數字化電能表被判定為達到期望準確度等級,否則認為不能達到期望的準確度等級。
2.3 隨機函數的選擇與檢定規則
實際信號在采樣過程中會引入各種模擬噪聲,產生B類不確定度,傳遞給離散化后的瞬時電壓、電流值,從而對被檢數字化電能表的測量準確度造成影響。由噪聲引起的B類不確定度與被檢數字化電能表自身的準確度等級無關。本文采用隨機函數來模擬實際信號采樣過程中引入的各種形態的噪聲,并根據被檢數字化電能表的準確度等級來設置隨機函數的參數。
隨機函數f(t)的選擇應滿足以下兩個基本條件:(1)隨機函數f(t)的平均值為0,方差可調;(2)隨機函數f(t)與正弦函數的相關系數為0(不產生功率)。集成電路的主要噪聲形態為高斯白噪聲和1/f噪聲。

表3 不同標準差的Gauss噪聲引起的B類不確定度

表4 不同標準差的1/f噪聲引起的B類不確定度

所以施加這兩種隨機函數時,標準差的大小應根據被檢數字化電能表的期望準確度等級設置,設置依據見表5、表6。
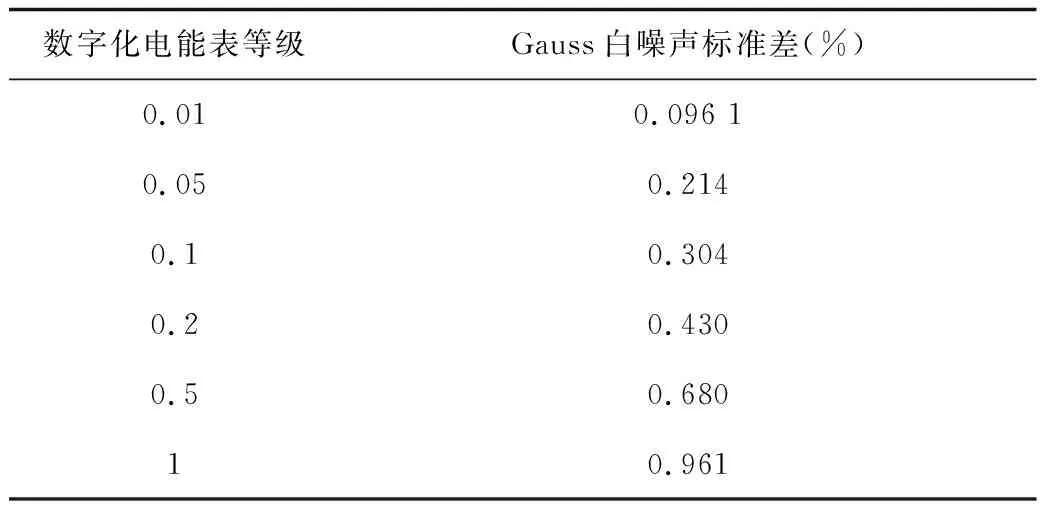
表5 高斯白噪聲標準差的設置容限
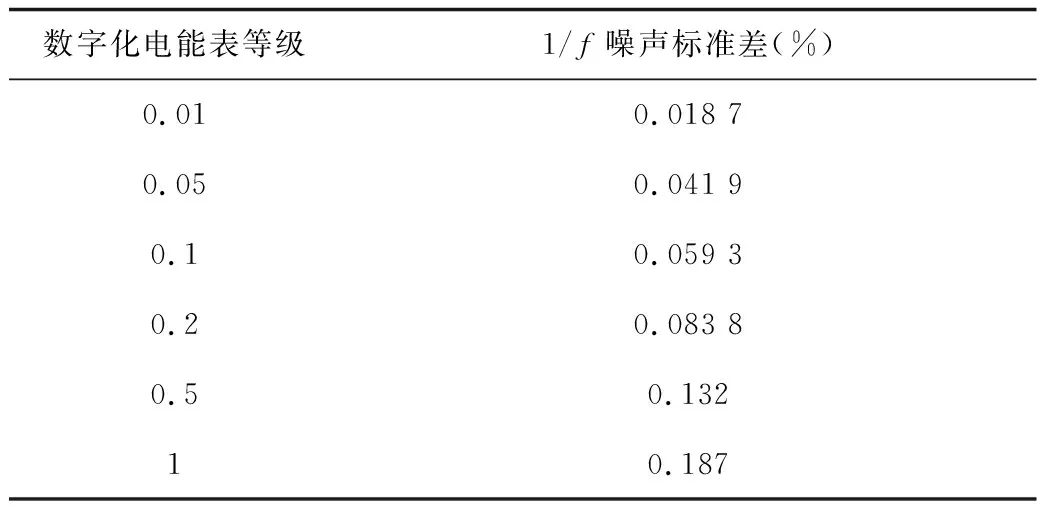
表6 1/f噪聲標準差的設置容限
檢定過程中施加的隨機函數f(t)是滿足上述規則的任何形式的隨機函數的線性組合,f(t)的表達式為:
f(t)=d1×f1(t)+d2×f2(t)+d3×f3(t)+…
(5)
式中f(t)為檢定過程中施加的隨機函數;f1(t)、f2(t)、f3(t)...為滿足上述規則的任何形式的隨機函數,數值精度為32位;d1、d2、d3……為組合系數。在合成不確定度符合要求的前提下,組合系數可自行決定,本文不作要求。
校驗步驟:
步驟1:施加隨機函數的標準差小于等于表5、表6中的容限,評估被檢數字化電能表的測量不確定度。例如,對期望準確度等級為0.1級的數字化電能表定級時,選擇標準差δ≤0.304%的Gauss白噪聲或標準差δ≤0.059 3%的1/f噪聲與標準數字功率源復合。若被檢數字化電能表的測量結果相對真值的不確定度S≤0.1%,則進行步驟2校驗;否則認為不能達到期望的準確度等級;

經過上述2步校驗,滿足條件的被檢數字化電能表被判定為達到期望準確度等級,否則認為不能達到期望的準確度等級。
2.4 諧波的選擇與檢定規則
實際電力系統中的諧波會產生功率波動,對電能表的測量準確度帶來影響。諧波影響下電能表實測電能值與時間的關系曲線圖如圖7中藍色實線所示,沒有諧波影響下的理論電能值與時間的關系曲線如圖7中黑色虛線所示。易見t1至t2時刻的實際累計電能值E2大于理論累計電能值E1,所以諧波對數字化計量系統的影響不可忽略,檢定數字表時應施加不同頻率的諧波以考察數字表的濾波性能。
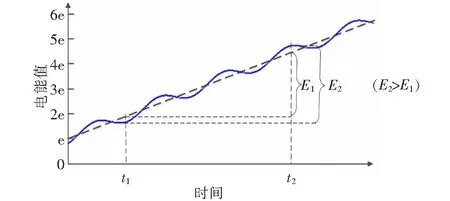
圖7 諧波影響下累計電能值與時間的關系曲線
考慮到諧波電流的影響,基波電流的表達式為:i(t)=Aisin(2π×f0×t+φi),基波電壓的表達式為:u(t)=Ausin(2π×f0×t+φu),頻率為fp的電流諧波的表達式為:ip(t)=Aipsin(2π×fp×t+θ)。則瞬時功率的表達式為:
p(t)=u(t)×(i(t)+ip(t))=
cos(2π(f0+fp)t+φu+θ))
(6)
式中有1個直流項和3個交流項,直流項即理論功率值。施加不同頻率的諧波時,造成諧波功率的主要項是式(6)中的第3項,根據濾波器的幅頻特性可確定施加諧波的衰減比進而確定施加諧波的最大幅值。
檢定數字化電能表時施加諧波的最高次數應滿足采樣定理的要求。以準確度等級為0.02級的數字化電能表為例,施加諧波的幅值應不超過圖8給出的要求。其中Am是電流諧波幅值Aip與電流基波幅值Ai之比,Am=Aip/Ai,Δf為諧波頻率fip與基波頻率f0的差,Δf=fip-f0。在滿足采樣定理的條件下,當Δf>100 Hz時,施加諧波幅值不應超過基波幅值。

圖8 施加諧波的幅頻特性
對其他等級電能表進行檢定時,施加諧波的幅頻特性曲線的形狀與圖8類似,表7給出一些典型頻率的諧波對應的幅值要求。

表7 施加諧波的幅值要求
3 實驗結果與分析
采用本文提出的檢定方案分別對4個不同廠家生產的準確度等級均為0.2S級的數字化電能表進行檢定,且這4個數字表采用傳統檢表法的檢定結果均為合格。
(1)施加隨機函數的檢定結果
由于集成電路中的首要噪聲形態為高斯白噪聲,本次實驗過程中施加不同標準差大小的高斯白噪聲形態的隨機函數并記錄數字化電能表的功率測量結果。4個數字表有功測量的相對不確定度如表8所示。

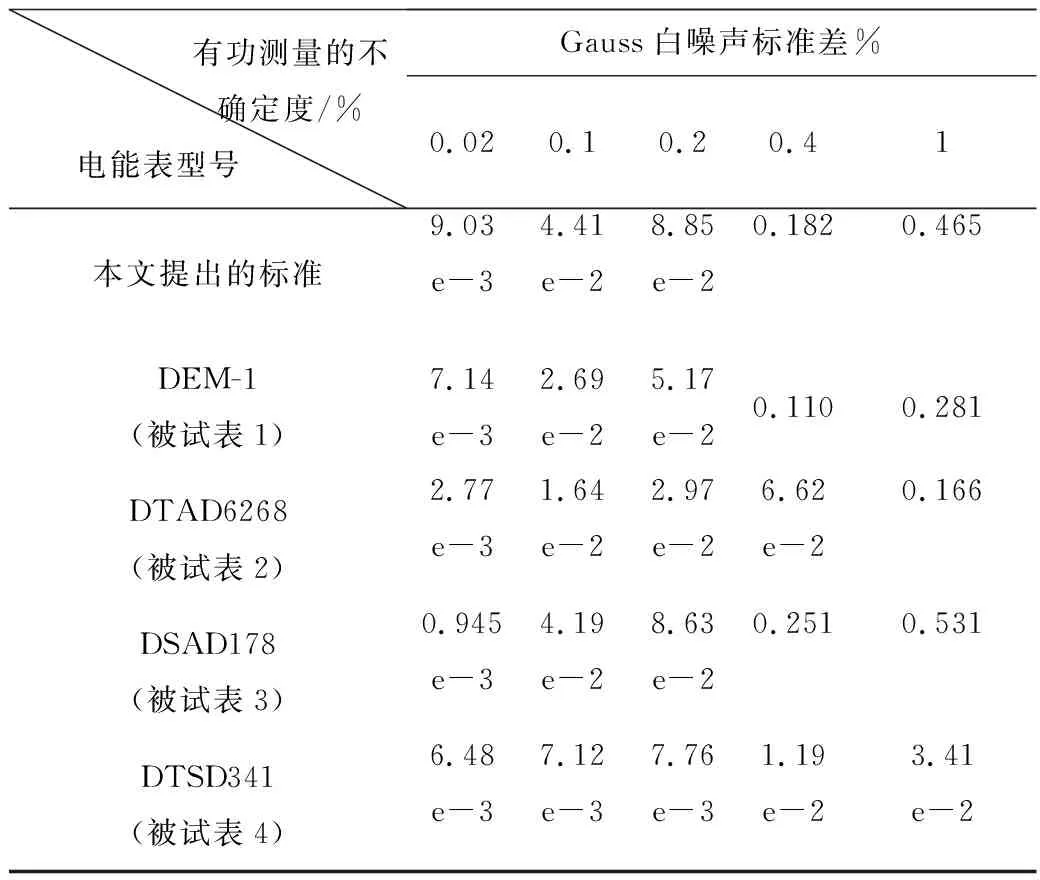
表8 施加隨機函數的檢定結果
(2)施加諧波的檢定結果
由2.3節可知,造成有功功率波動的主要諧波頻率范圍為50 Hz 由圖9可知,被試表4的濾波性能最優,施加100 Hz以上諧波的幅值可達到基波幅值的100%。被試表1在各個頻點處的濾波性能較好,滿足本文提出的濾波性能要求。被試表3對5 Hz的倍頻諧波的濾波效果突出,對低頻諧波的濾波效果較好,能夠滿足要求;但對120 Hz以上的諧波濾波效果較差,不滿足本文提出的要求。被試表2對50 Hz的倍頻諧波的濾波效果突出,但對105 Hz以上的諧波濾波效果較差,不滿足本文提出的要求。所以按照2.4節提出的校驗步驟進行檢定,被試表1和4被判定為能達到期望準確度等級0.02級,被試表2和3被判定為不能達到期望準確度等級0.02級。 圖9 施加諧波的幅頻特性 另外,4個被試表均采用數值精度為32位的數據幀計算分析,符合表2中提出的0.02級數字表應滿足的數值精度要求。 由本次實驗結果可知被試表4具有較好的濾波性能和噪聲抑制性能,它在不同噪聲和諧波環境下有功測量的相對不確定度均小于其他三個被試表。在實際應用中也證實了被試表4的可靠性最高,受到了業內人士的廣泛認可。本文討論的檢定方法區別于傳統檢表法能夠鑒別出不同廠家生產的數字化電能表的性能優劣,較科學地實現了對數字化電能表的檢定。另外,目前我國國家標準規定數字化電能表的最高準確度等級為0.2S級,本節實驗中所采用的四個數字化電能表在整體校驗方案中均被定級為0.2S級,但不表示數字化電能表本身的準確度不能達到更高的準確度等級,這是由于在整體校驗中得到的電能計量誤差不僅包括數字表本身的不確定度還引入了電子式互感器的測量不確定度。 首先,本文相對科學地解決了關于數字化電能表溯源問題的困惑,指出數字化電能表的實質是數值處理,只存在數值溯源,而不存在量的溯源的問題。如果要進行電能計量量值溯源,則必須對數字化電能計量系統的整體進行溯源。進而本文針對傳統標準源法在實際應用中存在的問題給出了詳細的描述,最后針對數字化電能表的檢定和量值溯源問題提出了一種新型的數值精度可調的標準數字功率源模型,即將三角函數形式的傅立葉級數與隨機函數相加所得的復合函數作為標準數字功率源的輸出形式,包含了實際測量系統中的模擬噪聲和諧波功率。本文詳細規定了不同情況下新型數字功率源的數值精度、施加的隨機函數和諧波的設置規則以及檢定步驟。這種基于新型標準數字功率源的方法可以有效地解決數字化電能表的檢定和溯源問題,在實際應用中有待進一步優化。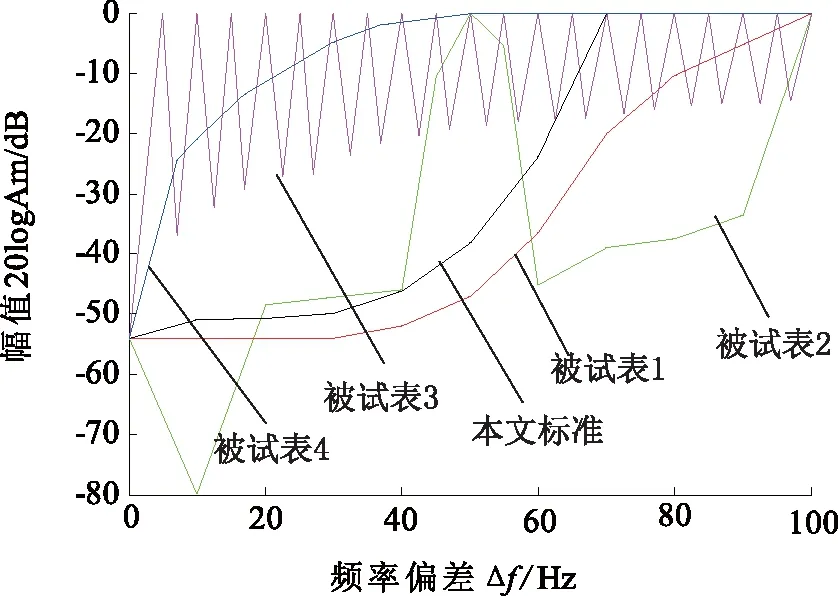
4 結束語

