基于灰色離散verhulst模型的天貓雙十一包裹量預測研究

趙雪琴

【摘要】近年來，天貓雙十一包裹量的增長呈現“S”形。灰色離散Verhulst模型是對灰色verhulst模型的優化，它不僅適用于具有飽和“S”型特征的數據序列，而且能消除由微分方程跳到差分方程時產生的誤差，從而使預測精度更高。通過建立基于灰色離散verhulst模型，對天貓雙十一包裹量進行中短期預測，可以為雙十一當天第三方物流企業的物流資源規劃與配置提供重要依據。

【關鍵詞】離散 verhulst模型 雙11包裹量 天貓

1 引言

2017年天貓雙11全天產生的包裹量高達8.12億個，導致短期內物流需求量暴增。第三方物流企業面對急劇增加的物流需求，常?！耙幻蛠y”，發貨時間延遲、物流配送中心爆倉、物流運輸及物流信息反饋不及時等問題層出不窮。因此，準確預測天貓雙十一包裹量，有助于第三方物流企業提前對整體物流資源進行更加合理、高效的配置。

天貓雙十一活動包裹量的增長呈現出飽和“S”形的特征，規律較為固定?；疑x散Verhulst模型是對灰色verhulst模型的優化，不僅對于近似飽和“S”型數據序列模型依然適用，且能消除由微分方程跳到差分方程時產生的誤差使預測精度更高。因此，本文選擇灰色離散Verhulst模型對天貓雙十一包裹量進行預測。

2 基于灰色離散verhulst模型的天貓雙+一包裹量預測

選擇2011年到2017年天貓雙十一包裹量作為原始數據（數據由中國電子商務研究中心每年官方發布的雙十一數據整理而得）。原始數據為：

X（0）=[2200，7800，15200，27800，46700，65700，81200]

由于原始數據本身呈S形，因此可以直接取原始數據為X（1），建立verhulst模型

直接對X（1）進行模擬。

Stepl：X0=[2200，7800，15200，27800，46700，65700，81200]

Step2：γ（0）=[0.000455，0.000128，0.000066，0.000036，0.000021，0.000015，0.000012]

Step3：γ（1）=[0.000455，0.000583，0.000649，0.000685，0.000706，0.000721，0.000733]

Step4：應用最小二乘法求解可得參數：

β=（β1，β2，β3）r=（0.000363，0.000005，0.473340）

Step5：灰色離散verhulst模型為

y（1）（t+1）=0.000363+0.000005t+0.47334y（1）（t）

Step6：求解灰色離散verhulst模型得模擬序列為：

X（0）=[2200，7788.11，15142.03，27607.23，45529.86，66026.81，84139.51]

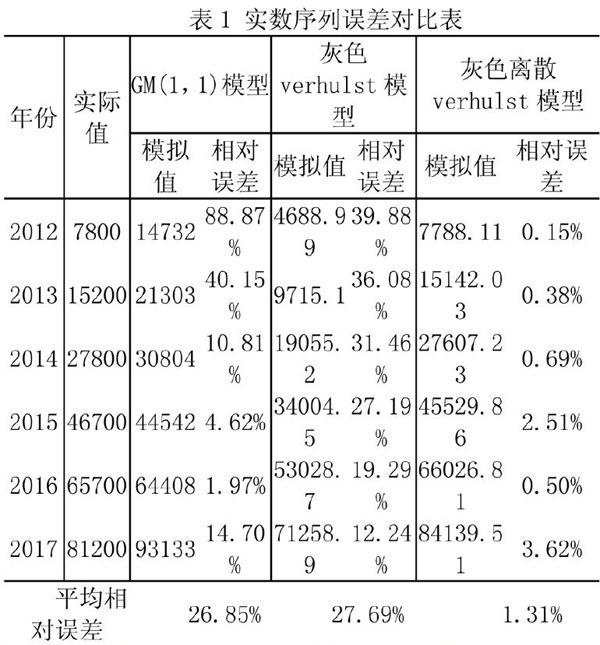
由計算結果可知：用灰色離散verhulst構建的天貓雙十一包裹量預測模型的精度高達98.69%，可以有效地對天貓雙十一包裹量進行預測。并與幾種典型的灰色實數序列預測模型預測模擬結果進行對比分析，發現灰色離散verhulst模型的模擬相對誤差整體低于GM（1，1）模型和灰色verhulst模型的模擬相對誤差，如表1所示。

綜上可以看出，基于灰數離散Verhulst模型相對于其他灰色實數序列預測模型的預測結果，表現出了良好的預測效果。

3 結論

本文構建的灰色離散verhulst的天貓雙十一包裹量預測模型，與其他經典灰色實數序列預測模型的預測效果相比，誤差更低，預測效果更好。因此，預測結果可以作為第三方物流企業提前規劃物流資源、做好物流業務流程安排的依據。