一種新型永磁同步電機滑模觀測器設計

柯希彪，任霄龍，郭琳

（1.商洛學院電子信息與電氣工程學院，陜西商洛 726000；2.西安科技大學測繪科學與技術學院，陜西西安 710054）

永磁同步電機（Permanent Magnet Synchronous Motor，PMSM）由于結構簡單、功率密度大、輸出轉矩大等優點，在現代工業、交通運輸等領域得到廣泛應用。永磁同步電機控制需要知道其準確的轉子位置信息和轉速信息。有位置傳感器的PMSM控制，檢測的轉子信息精度較高，但因位置傳感器的引入，使控制系統變得復雜，可靠性降低，同時一套性能優異的位置傳感器價格昂貴，增加了PMSM的使用成本。因此，采用無位置傳感器控制策略實現PMSM控制，是目前國內外學者研究的重要內容。文獻[1]提出一種基于Popov超穩定性理論的模型參考自適應（Model Reference Adaptive System，MRAS）觀測器控制策略，驗證了所設計模型具有較強的位置和轉速檢測能力；王慶龍[2]、柯希彪[3]等提出了一種基于滑模模型參考自適應（MRAS）策略的永磁同步電機控制策略[2-3]；侯利民[4-5]等設計出一種基于擴展滑模觀測器的無位置傳感器控制策略，引入鎖相環原理檢測電機轉速和位置信息；還有研究等將鎖相環（PLL）理論與滑模觀測器（SMO）模型相結合，獲得PMSM轉速和轉子位置信息[6-12]。本文在滑模觀測器控制基礎上，采用飽和函數和PLL原理將其進行改進，設計一種新型控制策略。在滑模觀測器中，因低通濾波器的引入，使得到的相位角有較大相位延遲，本控制策略采用雙低通濾波器對相位角進行實時相位補償。最后，搭建永磁同步電機仿真模型，從電機轉速跟蹤能力、位置檢測誤差和抗負載擾動能力三方面對控制系統進行分析，驗證所設計控制策略的有效性。

1 永磁同步電機矢量控制模型

PMSM是一種非線性、強耦合的系統，在搭建數學模型時，忽略次要的影響因素，對電機模型作以下假設：忽略磁路飽和，不計鐵芯渦流損耗和磁滯損耗；永磁材料電導率為零；轉子上無阻尼繞組；氣隙中磁場呈正弦分布。

隱級式PMSM在兩相旋轉坐標系(d-q軸)的數學模型[13-16]：

式中：iq、id分別為交、 直軸電流，uq、ud分別為交、直軸電壓，Rs為定子電阻，Ls為電樞等效電感，Pm為磁極對數，ωe為電角速度，ψf為轉子磁鏈，J為轉動慣量，B為粘滯系數，TL為負載轉矩。

PMSM 磁鏈方程[2-4，13-16]：

式中：ψd、ψq分別為交、直軸磁鏈。

電磁轉矩方程[2-4]：

本文所提出的控制策略是以永磁同步電機雙閉環矢量控制模型為對象展開的，矢量控制是一種無差控制策略，其控制精度較高，結構簡單，是最為常見的PMSM控制模型，內環控制為電流反饋環，外環為轉速反饋環；令i*d=0，則定子電流矢量超前轉子磁鏈90°，使得電樞電流完全用于提供電機電磁轉矩。

2 永磁同步電機滑模觀測器控制設計

2.1 永磁同步電機SMO模型

PMSM在兩相靜止坐標系（軸）的數學模型[2-4]：

式中，iα、iβ分別為 α、β軸電流分量；uα、uβ分別為α、β軸電壓分量；eα、eβ分別為 α、β軸反電動勢；θe為轉子相位角。

滑模觀測器（SMO）方程為[2-4]：

式中，“^”代表各變量的估計值；K為滑模觀測器開關增益；sign()為符號函數。

將式(6)減去式(4)，可得滑模觀測器（SMO）誤差狀態方程：

式中

當系統達到穩定狀態時，有：

那么，由式(7)可得：

可以近似得到PMSM兩相靜止坐標軸的等效反電動勢。

設計SMO滑模面為：

根據Lyapunov穩定性定律可得：

由式(12)可推導出SMO的增益為：

為了滿足系統穩定條件，由式(13)可知，滑模增益取值須足夠大。但值取的過大，運動點在滑模面附近會大幅高頻切換變量的控制狀態，易引起系統強烈抖振，降低了系統的動態品質，不利于系統穩定。本文在設計滑模觀測器時，選取對SMO開關增益進行實時調整，可以有效降低系統抖振。

為了減小由符號函數引起的系統抖振，本文采用具有連續變化特性的飽和函數代替符號函數，飽和函數設計為：

式中，a為正數，其值大小決定了飽和函數線性區域內滑模增益的變化幅度。當K的取值滿足式 (13)時，SMO依然可以滿足Lyapunov穩定條件。SMO模型設計如圖1所示。

圖1 SMO模型

其中，LPF表示低通濾波器（Low Pass Filter）。

由滑模觀測器（SMO）模型可得反電動勢等效模型為：

式(15)中，ωc為低通濾波器（LPF）截止頻率，截止頻率越小時，所得的等效反電動勢波形越光滑，反電動勢相位滯后越嚴重，需要補償的相位角就越大；當截止頻率接近或低于電機運行角頻率時，將無法檢測到正確的反電動勢，從而無法計算出電機的轉子信息，因此低通濾波器截止頻率不是越小越好。本文采用ωc≈10e的控制策略。

2.2 電機位置和轉速計算

通過飽和函數和低通濾波器（LPF）近似可得永磁同步電機軸反電動勢，在傳統滑模觀測器（SMO）中，采用的是反正切法求PMSM相位角和轉速：

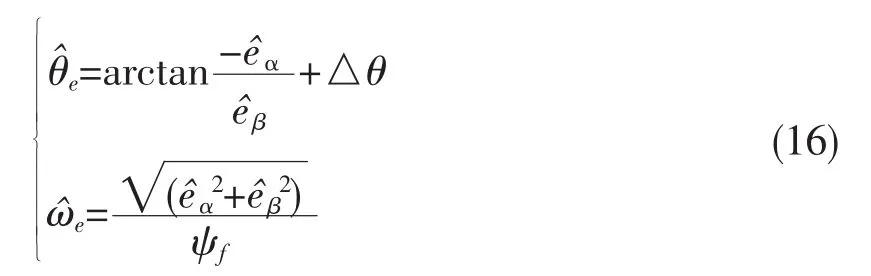
式中，△θ為低通濾波器引起的相位滯后角度，當電機轉速越大時，所需補償角△θ也越大，△θ近似為：

2.3 鎖相環控制原理

鎖相環（PLL）電路本身是一個反饋電路，它是通過將自身的相位反饋到輸入信息中，達到相位跟蹤的目的。與傳統的反正切法相比，可以有效降低系統抖振，使相位角自動跟蹤。同時，鎖相環電路計算量較小，無需引入復雜的三角函數。鎖相環（PLL）模型如圖2所示。

圖2 鎖相環(PLL)模型

其中，

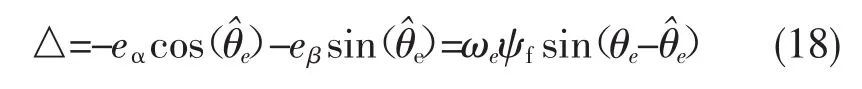
圖3 基于鎖相環（PLL）的SMO模型

2.4 雙低通濾波器（DLPF）補償控制策略

由于在計算等效反電動勢過程中，引入低通濾波器，使所得相位角存在相位滯后現象，需要對其進行相位補償，本文設計一種基于雙低通濾波器的補償策略，控制模型如圖4所示。

圖4 基于DLPF的SMO模型

兩個低通濾波器截止頻率相同，因此所檢測的反電動勢具有完全相同的相位滯后量，通過所求相位角作差，可求出一個低通濾波器的滯后相位，從而進行相位角實時補償；本策略可以有效避免傳統算法中當電機轉速超過預期范圍時，補償角度不足的問題，增大PMSM調速范圍。

3 仿真結果與分析

基于Matlab/Simulink搭建PMSM控制模型，實現PMSM滑模觀測器控制。在仿真模型中，直流側電壓為300 V，PMSM模型為Simulink中提供的模型，當θe=0°時，磁鏈的位置與A相一致，其參數如表1所示。

表1 PMSM參數

永磁同步電機矢量控制模型如圖5所示，采用空間矢量脈寬調制法（Space Vector Pulse Width Modulation，SVPWM）驅動逆變電路，對轉速環和電流環分別采用PI調節器進行控制。

圖5 PMSM矢量控制模型

對永磁同步電機進行基于雙低通濾波器（DLPF）補償的滑模觀測器控制策略仿真，并將其與傳統滑模觀測器（SMO）控制策略進行比較。用階躍信號分別模擬PMSM轉速調節和負載轉矩擾動，仿真時間設置為0～0.2 s。在0時刻，給定電機轉速為 1 000 r·min－1，運行到 0.06 s時刻，調節電機轉速由 1 000 r·min－1升為 2 000 r·min－1，在0.14 s時刻，給電機突加4 N·m的負載，仿真波形分別如圖6～圖8所示。

由圖6(a)和圖7(a)波形對比可知，在PMSM啟動和調速階段，SMO控制的PMSM控制和基于DLPF補償策略的PMSM控制都能夠迅速響應，在極短的時間內跟蹤到系統給定的轉速；在圖7(a)中，調速初始階段波形中存在較大超調量，由于滑模控制具有較強的抗干擾能力，使得電機轉速快速趨于穩定值，在圖6(a)中，調速初期電機轉速超調量很大，轉速波形不能趨于穩定值，而是在給定值附近持續反復波動；出現這種現象的原因是在傳統SMO控制中，檢測到的轉子相位角與實際相位角（如圖8）存在較大誤差，如圖6(e)所示，電機相位角估算不準確，導致交、直軸電流解耦不完全，出現較大波動）（如圖6（b）），影響到電磁轉矩（如圖6（c）），從而引起電機轉速控制出現劇烈抖動。

在基于雙低通濾波器（DLPF）補償策略的SMO控制中，由仿真波形可知，其轉子相位角估算誤差較小，如圖7(e)所示，交、直軸電流解耦誤差較小，如圖7(b)所示，使得電磁轉矩波形較穩定（如圖7(c)），最終，使PMSM可以達到較精確的轉速跟蹤效果。

在電機運行到0.14 s時刻，給電機突加負載的情況下，轉速經歷了一個短暫的波動后，迅速恢復到穩定值，如圖7(a)所示，表明控制系統具有較強的抗干擾能力，因此本文提出的基于雙低通濾波器補償的控制策略較傳統控制策略能夠更好的實現PMSM滑模觀測器控制。

圖6 SMO控制的PMSM仿真波形

圖7 DLPF補償的PMSM仿真波形

圖8 PMSM實際轉子相位角波形

4 結論

通過對永磁同步電機傳統滑模觀測器控制策略的研究并改進其控制策略，本文設計了一種基于雙低通濾波器補償的永磁同步電機滑模觀測器控制策略，目的在于提高控制系統的動態品質和抗干擾能力。最后，通過搭建仿真模型進行驗證，仿真結果表明，采用雙低通濾波器補償的控制策略檢測的相位角比傳統滑模觀測器檢測的相位角更準確，使得控制系統動態性能更優良，抗干擾能力更強，有效實現了永磁同步電機無位置傳感器控制。