強化數(shù)學思想方法，倡導課堂深度教學

廣東 王常斌

數(shù)學是思維的體操，數(shù)學學習的目的是使人變得聰明，讓學習者學會解決問題的一般方法和步驟.而長期以來，我們教學走入一個誤區(qū)，重知識的傳授而忽視了對學生能力的培養(yǎng)或者說忽視了對學生智力的開發(fā)，表現(xiàn)出來的現(xiàn)象或者是滿堂灌，或者是題海戰(zhàn)術(shù)，新課的講解缺少知識的發(fā)生發(fā)展過程，就像章建躍老師說的“一個定義，三項注意，幾個例題，大量練習”，這樣的教學培養(yǎng)的學生對知識理解不到位，知其然而不知其所以然，更達不到“何由以知其所以然”.只會死搬硬套，只會死做題，做死題，碰到真正靈活，需要有較多的思維參與的題，也難以考出高分.2016年新修訂的考綱中明確提出了從數(shù)學思想方法、數(shù)學能力、數(shù)學的科學與人文價值三個方面考查學生的數(shù)學學習情況，這體現(xiàn)了知識與能力并重、科學與人文兼顧的精神，同時也是對我們教學的一種導向.

在一次高三地市級組織的模擬考試中，某區(qū)的數(shù)學平均分與其他幾個區(qū)相比有優(yōu)勢，但一本上線人數(shù)卻并沒有領(lǐng)先，甚至還落后于有些區(qū).仔細分析得分情況，可以發(fā)現(xiàn)該區(qū)學生在基礎(chǔ)題方面做得相對較好，但在“難題”方面得分率很低，出現(xiàn)這種現(xiàn)象的原因是多方面的，經(jīng)過筆者的了解，其中一個很重要的原因在于教師在教學中缺少對學生數(shù)學思想方法上的訓練，教學缺乏深度，致使學生的能力達不到要求.因此我們應加強數(shù)學思想方法的教學，提倡深度教學、智慧課堂，以提升學生的數(shù)學素養(yǎng).下面舉例進行說明.

一、分類討論思想

【例1】(理7)五個人圍坐在一張圓桌旁，每個人面前放著完全相同的硬幣，所有人同時翻轉(zhuǎn)自己的硬幣.若硬幣正面朝上,則這個人站起來;若硬幣正面朝下,則這個人繼續(xù)坐著.那么,沒有相鄰的兩個人站起來的概率為

( )

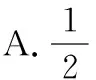
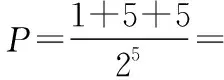
教學啟示：本題是一模理數(shù)第7題，文數(shù)第7題為姊妹題，只是將題中的五個人改成了四個人而已.此題文科得分率37%，理科得分率36%，考慮到是選擇題，故學生實際掌握此題的應該不超過20%.為何得分率這么低？主要是分類討論思想掌握不好，不知道將“沒有相鄰的兩個人站起來”分成3種情況來處理.因此，我們在評講此題時要告訴學生解題時要從思想方法的角度去思考.

分類討論思想是一種重要的數(shù)學思想方法，在高中階段很多時候會用到，如解雙絕對值不等式的問題，含參數(shù)的函數(shù)求單調(diào)區(qū)間問題等，它在高中階段的每個知識版塊中均會涉及.分類討論思想一定要弄清楚兩個問題：一是在什么情況下要分類討論；二是分類討論的標準是什么.另外分類時要做到不重不漏，教學中一定要適時滲透分類討論思想，不能就題講題.

二、函數(shù)與方程思想

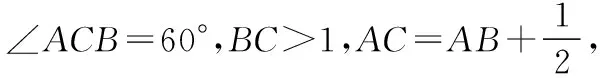
試題分析：本題考查正弦定理、余弦定理的應用，考查利用均值不等式或判別式法求最值，考查函數(shù)與方程思想.基本思路：

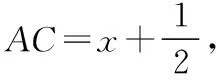
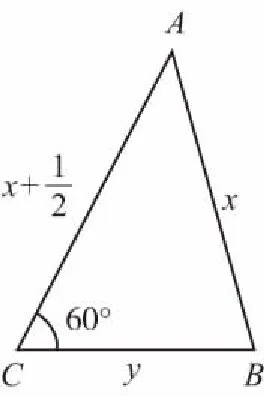
設(shè)△ABC的周長為m，根據(jù)題意可得

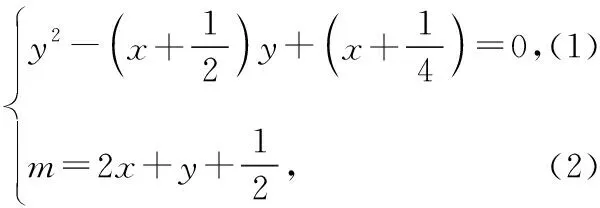
共有三個未知數(shù)，按常規(guī)思路，必須列出三個方程才能解出未知數(shù)的值，但我們只能列出兩個，故還需要一個條件才能求出未知數(shù)的值.細讀題目，我們發(fā)現(xiàn)還有一個條件未用，即“△ABC的周長最短”，這個條件就可以考慮用函數(shù)求最值的方法來處理，由此我們有以下兩種思路：

思路1：因為(1)式中x為一次項，故很容易用y表示出x，然后代入(2)式，通過基本不等式或?qū)?shù)求函數(shù)m的最值，從而求出y的值.

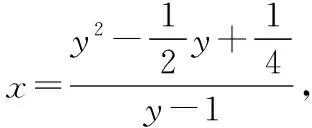
思路2：因為(1)式是關(guān)于y的一元二次方程，故可用判別式法來求值域.

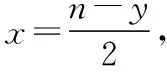
6y2-2(n+2)y+(2n+1)=0， (3)

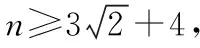
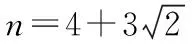
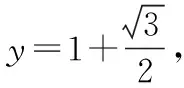
本次考試中文數(shù)17題，考查數(shù)列，其中第一問也用到了函數(shù)與方程的思想.在教學中我們應加強函數(shù)與方程思想的教學，利用函數(shù)與方程的思想來指導我們解決相關(guān)問題.

三、轉(zhuǎn)化與化歸思想

【例3】(文理10)《九章算術(shù)》中，將底面為長方形且有一條側(cè)棱與底面垂直的四棱錐稱之為陽馬;將四個面都為直角三角形的三棱錐稱之為鱉臑．若三棱錐P-ABC為鱉臑,PA⊥平面ABC,PA=AB=2，AC=4,三棱錐P-ABC的四個頂點都在球O的球面上,則球O的表面積為

( )

A.8π B.12π C.20π D.24π

試題分析：本題文理同題，均為第10題，它考查對立體幾何中基本圖形——陽馬、鱉臑的識別，球的表面積計算，考查學生對割補法的掌握，考查學生的作圖能力、運算求解能力以及轉(zhuǎn)化的數(shù)學思想.解題的基本思路如下：

思路1：直接找出球心為PC的中點O，從而求出球的半徑，進而計算球的表面積.

思路2：將鱉臑補形成長方體，長方體的外接球就是鱉臑的外接球.

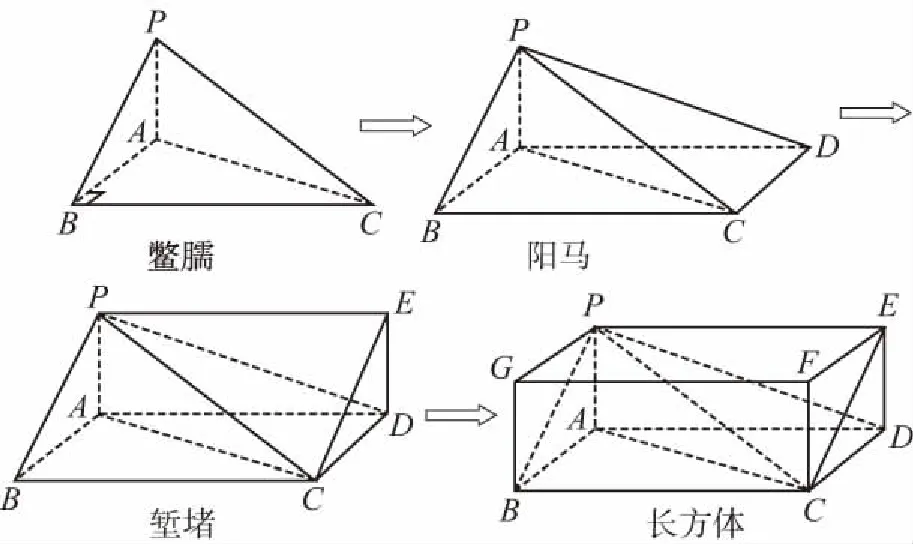
教學啟示：此題也是在考題中滲透中國古代數(shù)學文化的一種體現(xiàn).上學期高二文數(shù)是填空題，此題平均分0.62，得分率為0.124，即只有約1/8的學生能做對，本次一模為選擇題，理科的得分率為44%，文科的得分率為38%，排除一些誤打誤撞的，本題真正掌握和理解的學生也就在1/3左右.上面的兩種思路中，思路1直接找出外接球的球心對多數(shù)學生是較難的，但如果我們在平時的教學中能對課本中的內(nèi)容(本題圖來自必修2課本69頁的探究題)適當?shù)淖鲆恍┭a充與拓展，學生明白陽馬和鱉臑是由長方體分割而來的，就馬上會想到利用思路2將此題求鱉臑的外接球表面積轉(zhuǎn)化為求長方體的外接球表面積，學生還會覺得難嗎？思路2就采用了轉(zhuǎn)化的數(shù)學思想，將不熟悉的問題轉(zhuǎn)化為熟悉的問題來解決.轉(zhuǎn)化的數(shù)學思想在我們的學習中司空見慣，因此我們一定要強化轉(zhuǎn)化與化歸的數(shù)學思想，靈活地運用轉(zhuǎn)化與化歸的數(shù)學思想會給我們帶來許多意想不到的收獲.如下例：

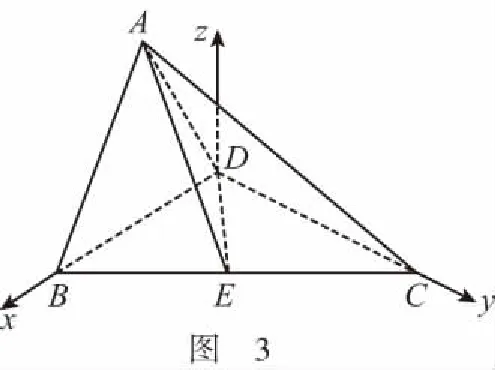
【例4】(理19)如圖1，在直角梯形ABCD中，AD//BC，AB⊥BC，BD⊥DC,點E是BC邊的中點,將△ABD沿BD折起，使平面ABD⊥平面BCD，連接AE,AC,DE,得到如圖2所示的幾何體.

(Ⅰ)求證：AB⊥平面ADC；

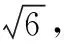
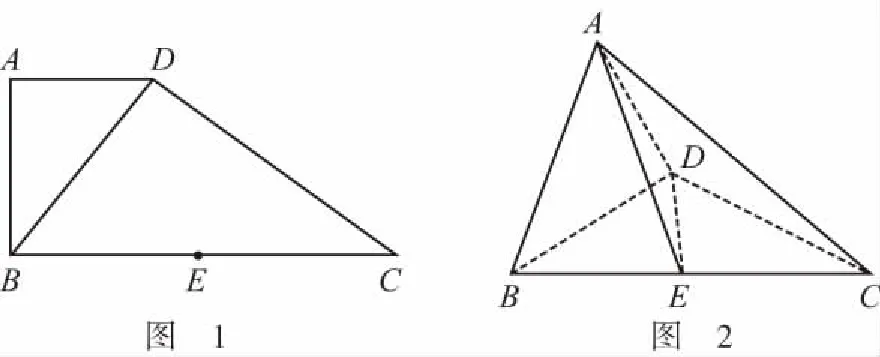
本題為此次模考的理科第19題，學生的得分率較低，特別是第二問全區(qū)得分率才10.4%，難點有幾個：一是不會根據(jù)題目條件求線段AB的長；二是不會合理建系；三是建系后不會求某些點的坐標.如有些同學按如圖3所示進行了建系卻寫不出點A的坐標.實質(zhì)上還是學生對立體幾何基本圖形缺乏認識，我們看三棱錐A-BCD的四個面均為直角三角形，它就是一個鱉臑！只是它的擺放不符合我們的視覺習慣而已！根據(jù)第一問可知，圖中本來就有三條兩兩互相垂直的線段：AB,AD和DC，只是它們沒有交于同一點，如果我們將此圖形進行適當?shù)男D(zhuǎn)變換，讓平面ABD水平放置，如圖4，建系就很容易了.因此最合理的建系，是下面的圖5，這樣建系是最易寫出坐標的，計算也相對容易.

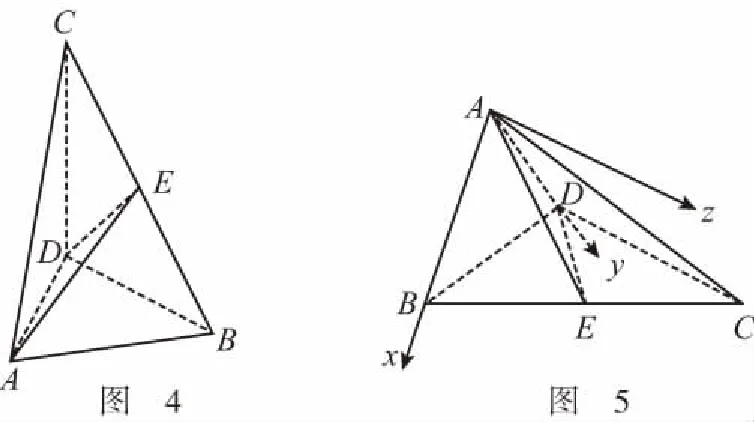
可見，轉(zhuǎn)化的數(shù)學思想有多么重要，我們在教學中一定要反復強調(diào)，經(jīng)常訓練，要讓學生善于聯(lián)想，將陌生的問題與我們學過的、見過的內(nèi)容聯(lián)系起來，經(jīng)過適當?shù)淖儞Q，將新問題轉(zhuǎn)化為舊問題來解決.

四、數(shù)形結(jié)合思想

( )

試題分析：本題考查三角函數(shù)的圖象與性質(zhì)及定積分的應用，考查運算求解能力、推理論證能力及數(shù)形結(jié)合思想.解題思路：

根據(jù)題意可畫出如下草圖.

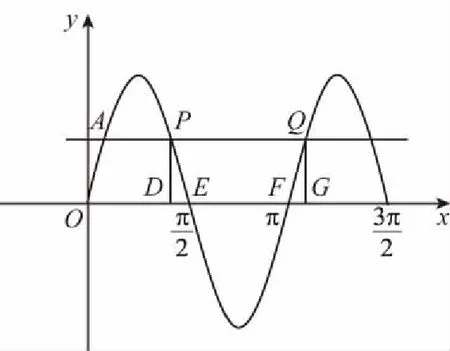
思路3：用估算法，如圖，根據(jù)正弦函數(shù)的對稱性，可將所求的面積轉(zhuǎn)化為圖中陰影部分的面積，顯然它大于矩形LMNK的面積，而SLMNK=|MN|·|LM|=π，故所求的面積應大于π，而選項中B,C,D均小于π，故選A.

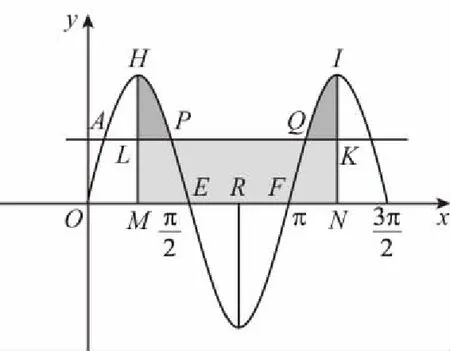
教學啟示：本題學生的得分率為29.5%，得分率如此之低，一是有些考生不能正確畫出圖形；二是sin2x的原函數(shù)求錯；三是大多數(shù)同學是按思路1來做的，一部分列式會出錯，而且運算較復雜，即使列式正確，運算也可能出錯，所以此題若利用思路2來求，列式和計算都會簡單很多.課本上雖然沒有直接給出思路2中的計算公式，但我們在教學過程中要引導學生推導出此公式，并利用此公式來求曲邊梯形的面積.思路3利用數(shù)形結(jié)合思想可很快得出答案，體現(xiàn)了小題小做的解題靈活性，但也有個缺點，假如此題換成填空題，或者有兩個或兩個以上選項大于π，則此法失靈，故思路3有一定的局限性.所以綜合來看，我們覺得思路2是一定要掌握的.此題無論采用哪種思路來解題，正確畫出圖形是基礎(chǔ)，所以此題考查了數(shù)形結(jié)合思想，特別是思路3，將數(shù)形結(jié)合思想體現(xiàn)的淋漓盡致.

五、對稱思想

( )

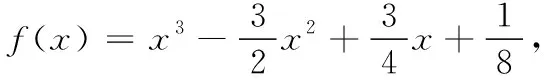
A.0 B.504 C.1 008 D.2 016

試題分析：本題考查三次函數(shù)的對稱性，倒序求和法，考查運算求解能力，對稱思想在函數(shù)中的應用.解題基本思路：

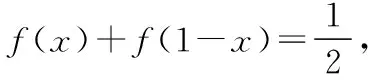
思路2：函數(shù)f(x)是三次函數(shù)，它的二階導數(shù)為0的點是其拐點，即函數(shù)的凸凹性發(fā)生改變的點，三次函數(shù)是中心對稱圖形，其拐點是其對稱中心的橫坐標.