基于浸入邊界算法的振動二維矩形柱繞流模擬研究

楊 青， 曹曙陽， 周軍文

(1. 安徽建筑大學 土木工程學院，合肥 230601; 2. 同濟大學 土木工程防災國家重點實驗室，上海 200092;3. 常州工學院 常州市建設工程結構與材料性能研究重點實驗室，江蘇 常州 213032)

振動鈍體繞流是一類具有廣泛工程應用背景的流固耦合問題，其普遍存在于大跨橋梁結構、高層建筑以及風力發電設備中[1-3]。柱體作為上述各類結構中常見的鈍體斷面形式，更是成為此類基礎研究領域的重點。

早期振動柱體研究多借助于風洞試驗完成[4-5]，近年來，隨著計算理論和硬件設備的發展，越來越多的學者傾向于利用CFD技術研究此類繞流問題。

Singh等[6]利用有限體積法模擬雷諾數Re=100和150時，不同強迫振動頻率下的方柱繞流，詳細分析了方柱鎖定區內的氣動系數及流場特征；Placzek等[7]采用有限體積方法模擬出Re=100時強迫振動的二維圓柱繞流，通過柱體升力系數隨振動頻率和振幅的變化曲線分析柱后尾流特征；國內徐楓、歐進萍[8]則借助Fluent研究Re=150時不同截面形狀對柱體振動形式的影響；丁林等[9]進一步在高雷諾數范圍(30 000≤Re≤110 000)展開不同截面形式柱體流致振動問題的研究，發現柱體流致振動振幅和頻率與尾跡旋渦形態緊密相關；劉志文等[10]采用“剛性運動區域+動網格區域+靜止網格區域”的思路建立網格，利用Fluent對寬高比為4的矩形斷面渦激振動響應進行了數值模擬，其研究結果與已有文獻風洞試驗結果的吻合性，證明了Newmark-β方法結合動網格技術的可行性。

然而，傳統CFD技術在求解振動鈍體繞流問題時，多需借助動網格技術，計算耗費較高。相比之下，浸入邊界方法(Immersed Boundary Method，IBM)利用力源擬化邊界的思想，直接可在靜止網格體系中實現振動鈍體的邊界再現，略去網格再生步驟，能夠顯著減輕計算負擔，且保證較好的計算精度。Luo等[11-12]從此類算法理論基礎入手，致力于提高此類方法在動態鈍體數值求解的精度；Chern等[13]則利用IBM模擬圓柱在Re=100～300時兩種不同自由度(豎向及扭轉)設置下的風致振動，研究發現：單一豎向自由度工況時，圓柱在鎖定區初始時刻，振動較大；雙向自由度工況時，圓柱尾部流場渦型由P型向2C型轉換；鐘國華等[14]也基于IBM研究了均勻流場中圓柱的振動問題，研究顯示：圓柱阻力在運動過程中一直存在振蕩，在最大振幅位置處，阻力與已有數據對比，呈現較大的數值差異。

綜上所述，振動柱體繞流研究目前仍多集中于方柱、圓柱等基本外形，對于實際建筑結構中同時出現“分離”和“再附”現象的鈍體斷面，則鮮有涉及。IBM雖然可以更高效地應用此類結構繞流的研究，但因其早期過多關注于算法改進，現有文獻僅在輪機、活塞等工程簡化研究問題中作出嘗試[15-16]，少有針對土木結構流固耦合繞流模擬的應用。因此，系統地開展不同邊長比下振動柱體的繞流研究，具有較高的工程應用價值。

本文基于IBM核心概念，編寫了數值計算模型，在Re=1×103時，展開不同邊長比下豎向強迫振動矩形柱的繞流研究，其中柱體運動軌跡為y(t)=Asinφ=Asin(2πfct)，式中y(t)為物體軌跡，A為振幅，fc為振動頻率，t為時間。模擬中振幅恒定為柱體迎風面高度的14%，以便同已有文獻數據結果對比。柱體邊長比B/D=1，3，5，分別對應柱體流動完全分離階段及再附階段。通過渦脫鎖定區、流場特征、氣動力系數三個方面的討論，研究不同邊長比下振動柱體的繞流，豐富IBM在工程領域中的基礎研究。

1 數值模型

本文數值模型以IBM為基礎，結合雙線性插值(Bi-linear interpolation method)和內部流體處理方法(Internal flow treatment)，以實現不同邊長比柱體的強迫振動繞流模擬。下文即對對該數值模型展開詳細介紹。

1.1 IBM控制方程

IBM利用流體與物體邊界相互作用的力學概念，將物體邊界簡化為作用于邊界點上的力源，并引入至Navier-Stokes方程中參加流場迭代計算，進而演化出邊界的幾何形狀和物理特性(式(1)～(2))：

(1)

(2)

式中：ui、uj為流體速度；ρ為流體密度；P為壓力；ν為流體運動黏性系數；Fi即為邊界力源，施加于圖1中邊界點上。

圖1 浸入邊界示意圖Fig.1 Illustration of immersed boundary

邊界力源Fi采用反饋構造形式，其力源概念更加清晰，反饋循環的應用也使其能夠實現較高的邊界數值精度，計算式為

式中：αf和βf為反饋系數項，其取值直接關系到邊界擬化效率；ui(sur)為邊界控制點處流體速度，由流體控制方程計算得出；Vdesired為物體邊界設定速度，靜止狀態時其值為零，若物體處于強迫振動狀態時，Vdesired可由振動方程計算得出；ui(sur)-Vdesired為邊界處流體速度與邊界設定速度的差異，表達式(3)正是基于此差異，通過反饋系數回饋出邊界力源使兩者速度接近，以滿足無滑移剛性邊界條件。內部流體則選用自由發展方法展開處理。

1.2 振動邊界實現技術

IBM模型的計算核心在于獲取實時邊界控制點處流體速度ui(sur)，用以構造邊界力源，進而迭代出鈍體外形。本次模擬對象為振動邊界，且計算網格采用交錯網格，邊界控制點很難與速度網格點重合，如圖2所示。

圖2 振動邊界示意圖Fig.2 Illustration of oscillating boundary

圖2中振動狀態下的邊界控制點E位置隨時間發生改變(Etn—Etn+1)，此時邊界速度不能由流體控制方程直接求得。因此，為保證邊界控制點速度的實時獲取，需借助本節開始所介紹的雙線性插值方法完成周圍速度網格定義點與邊界控制點之間的數據傳遞。

雙線性插值方法，其過程分為兩個步驟：速度獲取和力源分配。

圖3 雙線性插值方法示意圖Fig.3 Illustration of bilinear interpolation method

其中速度獲取如圖3(a)所示，邊界控制點速度u(E)可由周圍速度定義網格點插值得出，具體插值公式為

(4)

式中：ui,j為插值所需速度網格定義點；φi,j為在插值過程中起到關鍵作用的雙線性函數，其一般形式為

(5)

式中:Δ(xi)和Δ(yi)為二維計算網格間距；(xE,yE) 為邊界控制點E所處坐標; (xi,yi) 則表示為各插值點坐標值。

力源分配則是指力源在邊界點構造完成后再分配到周圍速度定義網格點上參與計算的過程。圖3(b)為該步驟示意圖。

F(ui,j)=φi,jF(uE)

(6)

式中:F(uE)為邊界控制點力源項；F(ui,j) 為插值網格點處力源值;φi,j為式(5)所示，表示雙線性函數。

具體至本文振動矩形柱繞流模擬，首先設計出定位模塊，根據物體振動軌跡計算出某一瞬時邊界點的運動坐標，其次依據插值方法迅速確定邊界點周圍的速度定義點，利用邊界插值函數獲得邊界點處流動參數以構造邊界力源，最后再將邊界力源分配到周圍速度網格定義點上，以參與該瞬時流場的整體計算，進而實現對運動邊界的擬化。圖4為本文振動邊界實現技術流程圖。

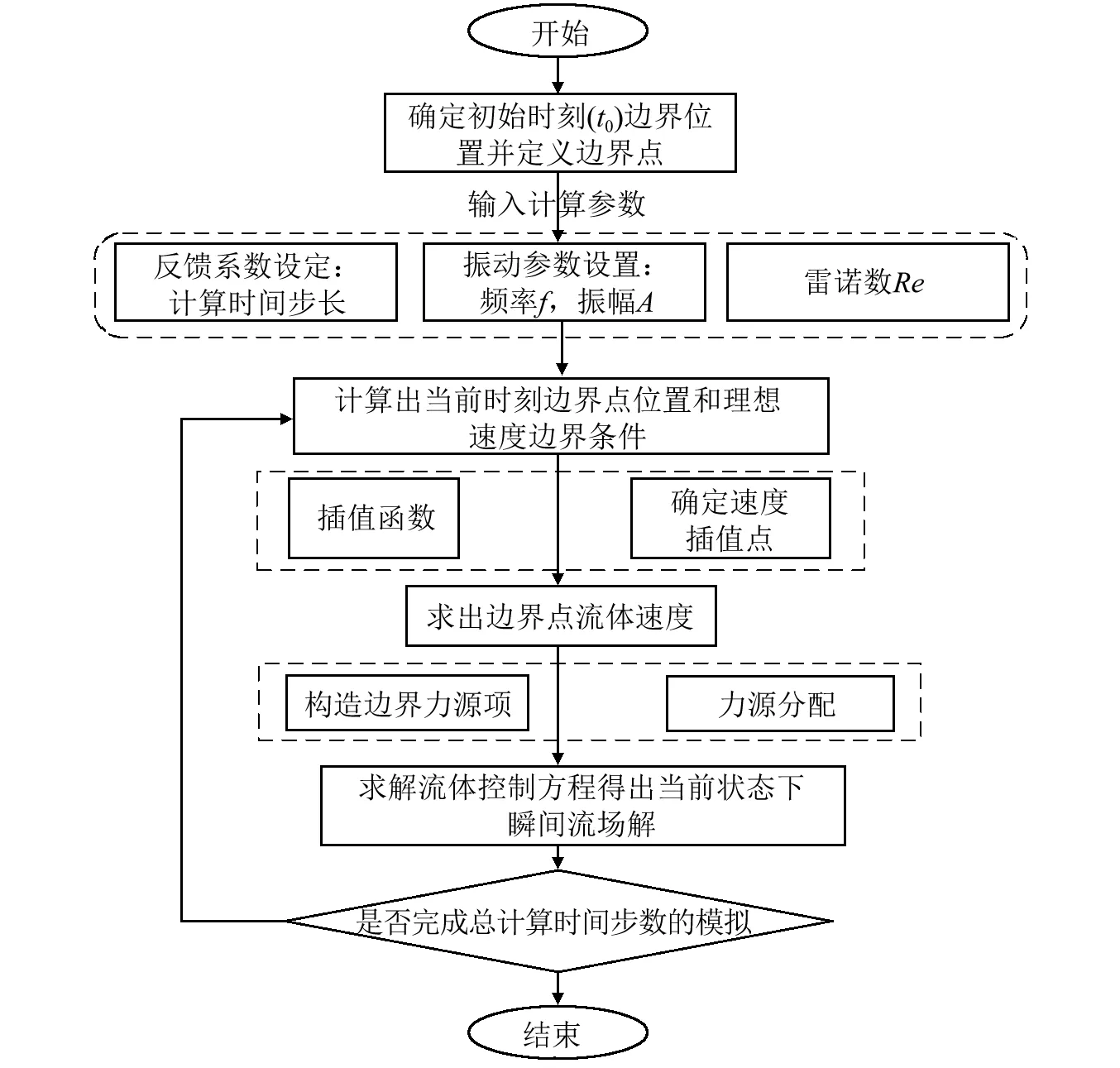
圖4 振動邊界實現技術流程圖Fig.4 Sketch of realization technique for moving Boundary

2 繞流計算域說明

本次振動矩形柱繞流均采用二維非均勻計算網格。流體從計算域左端施加，流動從左至右。邊界條件統一設定為：入口邊界條件u=1.0，v=0；出口邊界條件采用對流邊界條件：?u/?t+um▽u=0；即流動變量除壓力項外其余的邊界梯度值為零。上下邊界條件設定為無摩擦邊界：?u/?y=0; ?P/?y=0;v=0。力源反饋系數取值為αf=-1.6×105；βf=-60。

柱體繞流計算域中，特征尺寸取為柱體迎風面高度D，計算區域中入口距方柱中心距離為10D，出口邊界則設置為31D。上下計算域邊界長度為H，D/H設定為1/28。考慮到方柱運動軌跡為豎向強迫振動，為增強柱體表面流動細節的捕捉，在其寬度B范圍內，沿零時刻柱體上下表面各設置尺寸為D×B的均勻網格區域，格子大小統一選為0.01D。超出此區域，則設置拉伸網格，網格總數為412×242；時間間隔Δt為1.5×10-4，計算域布置如圖5所示。

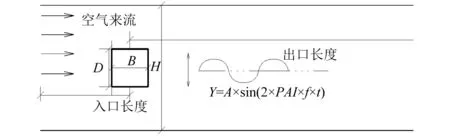
圖5 振動方柱計算域示意圖Fig.5 Illustration of calculation domain for oscillating rectangular

3 數值驗證

為驗證本文程序可靠性，首先利用該動態程序模擬Re=103，A=0，邊長比B/D=1的靜止方柱繞流。

圖6 方柱時均化表面壓力分布曲線Fig.6 Distribution curve of mean pressure coefficient Cp for square cylinder at Re=103

圖6為Re=103時方柱表面壓力分布。圖中可以看出柱體前緣表面壓力分布與Cao 等[17]數據基本吻合，方柱其余表面壓力分布特征亦吻合較好，但其值略大。原因可能存在于本文模擬為二維模擬，模擬維度的不同導致了流動分離時流場結構的差異性變化，進而影響到方柱表面壓力分布。

圖7 方柱尾流區時均流向速度分布Fig.7 Mean stream velocity in wake region of square

圖7為方柱尾流區平均流向速度分布，U為入口參考流速。圖7(a)中x/D=0處方柱平均流向速度分布，由于其在鈍體尖銳邊角的流動分離會而造成的分離層內壓力下降，導致尾流區流體的動量虧損，尾流區內速度減小，在偏于中心線的部分存在速度最小值；圖7(b)中x/D=1處，由于已經遠離方柱，此效應減弱，速度經過展現延伸后，趨于回歸到來流風速。方柱此時模擬所得St為0.133，與Cao等所得結果0.129基本吻合。

在此基礎上，展開模擬Re=103，A=0，邊長比B/D=5的方柱繞流。

圖8 矩形柱渦量圖(B/D=5)Fig.8 Vortex contour of rectangular (B/D=5)

圖8為邊長比B/D=5的矩形柱渦量圖。此時，矩形柱繞流已完全進入沖擊剪切層階段，柱體側面附著渦形狀不再穩定，渦脫結構更加復雜。柱后流場結構完全由柱體前緣流動分離所決定。本文模擬所得流場特征圖符合Nakamura等[18]的研究描述。

進一步將本次模擬所得不同邊長比矩形柱斯托羅哈數St(D)(Re=103)與Nakamura等對比，如表1所示，可以看出，本文數值結果吻合較好。

表1 不同邊長比矩形柱St(Re=103)

上述各類計算數據的吻合驗證了本文IBM算法程序的可行性和準確性。

4 振動柱體繞流模擬

振動矩形柱繞流計算中，關鍵無量綱參數包含：Stc=fcD/U，Stv=fvD/U，Stn=fvnD/U；其中fc為強迫振動頻率，fv為振動柱體渦脫頻率，fvn則代表靜止渦脫頻率；D為柱體高度；U為來流速度。

本節著手展開Re=1×103，振動頻率Stc=0～0.5、振幅A=0.14D的不同邊長比(B/D=1，3，5)強迫振動柱體的繞流模擬，分析柱后尾流渦脫特征，并結合柱后近尾跡流場顯示、氣動力系數以及氣動穩定性三個方面，探索邊長比效應對振動柱體繞流氣動特征的影響。

4.1 渦脫頻率分析

本次模擬參照Nakamura等的試驗設置，亦在柱體后部1.5D處設置速度觀測點，用以收集流場速度時程數據，通過對其作頻譜分析，繪制出振動矩形柱尾流渦脫隨振動頻率變化的曲線。

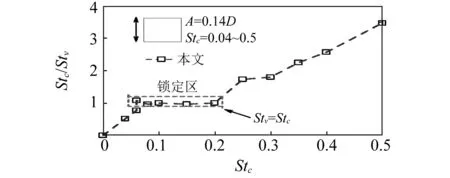
圖9 方柱渦脫隨振動頻率變化曲線(B/D=1)Fig.9 Variation of frequency ratio for squares with varying oscillating frequencies(B/D=1)

圖9為方柱渦脫隨振動頻率變化曲線，通過速度頻譜分析得出其鎖定區長度(Lock-in region length)為0.06～0.2。當外加強迫振動頻率Stc超過0.2時，柱體尾流渦脫頻率回歸靜止渦脫的現象十分突出，并一直保持，使得振動頻率與渦脫頻率的比值(Stc/Stv)呈線性分布特征。本次模擬主要特征與Singh等得出的現象吻合，驗證了本次模擬的可靠性。Taylor等[19]定義鎖定區中Stc=Stv=Stn的點，為共振鎖定點(Resonant point)，此時外加振動頻率與靜止渦脫頻率完全保持一致，本次模擬中方柱(B/D=1)共振鎖定點為0.133。

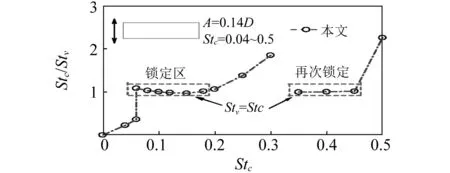
圖10 B/D=3時柱體渦脫隨振動頻率變化曲線Fig.10 Variation of frequency ratio for rectangular(B/D=3)with varying oscillating frequencies

圖10為B/D=3時矩形柱渦脫隨振動頻率變化曲線。圖中可以看出：與振動方柱對比，矩形柱(B/D=3)渦脫亦在外界振動頻率Stc=0.06時進入鎖定區，柱體尾流渦脫頻率與外界振動頻率保持一致；當振動頻率提升至Stc=0.2時，柱后尾流旋渦脫鎖，振動柱體渦脫頻率回歸到靜止時渦脫頻率(Stn=0.178)；但不同于方柱(B/D=1)，此后繼續增大強迫振動頻率，至0.35時柱體再次進入鎖定區，出現了呼和敖德同類試驗所指出的多級鎖定現象[20]，并一直持續到Stc=0.45，此后柱后尾流渦脫再次脫鎖并接近靜止渦脫頻率。

圖11 觀測點速度頻譜圖(B/D=3)Fig.11 Frequency spectrum of observation point’s velocity(B/D=3)

圖11為矩形柱(B/D=3)尾流速度頻譜分析圖，圖11(a)可以看出Stc=0.25時，靜止渦脫頻率在尾流流場中起到控制作用，雖然振動頻率響應部分也有明顯的峰值，但仍小于靜止渦脫頻率部分，符合超越鎖定區后的脫鎖現象。圖11(b)Stc=0.35時，強迫振動頻率已基本控制柱后尾流渦脫，靜止渦脫頻率部分對柱后尾流渦脫的影響遠小于外界激勵部分。此前研究振動柱體繞流的文獻，多集中于運動振幅增加對方柱渦脫頻率、氣動力系數的影響，鮮有對于邊長比效應在此方面的研究。Nakamura等[21]雖然對不同邊長比柱體的相位差、升力系數頻響虛部值展開了分析，也并未明確標示出不同邊長比下柱體渦脫鎖定區情況，但其研究中升力系數頻響虛部值兩次轉正的現象也從側面說明柱后尾流渦脫多級鎖定的情況。

圖12 邊長比B/D=5柱體渦脫隨振動頻率變化曲線Fig.12 Variation of frequency ratio for rectangular(B/D=5)with varying oscillating frequencies

繼續增大邊長比至B/D=5，頻譜分析其速度時程，得出渦脫隨振動頻率變化曲線，如圖12所示。圖中可以看出，柱體在強迫振動頻率Stc=0.15處才開始進入鎖定區，此時柱體渦脫頻率完全由外界振動頻率所控制；鎖定區長度有所延長，Stc=0.5時柱體渦脫頻率仍處于鎖定區；強迫振動頻率升高至Stc=0.6時，柱體尾部旋渦已經脫鎖，靜止渦脫頻率重新控制尾流流場。

4.2 流場顯示

流場顯示對于分析不同強迫振動頻率下鈍體近尾跡流場特征十分重要，除此之外，流場顯示還可用以分析鈍體在不同振動頻率下的氣動力系數特征，揭示鎖定區尾流渦脫作用的流動機理。

圖13為Stc=0.1時振動相位分別為6π、8π的方柱流場渦量圖，結果顯示：柱后渦脫頻率與強迫振動頻率保持一致，柱后渦脫基本呈現周期性再現。

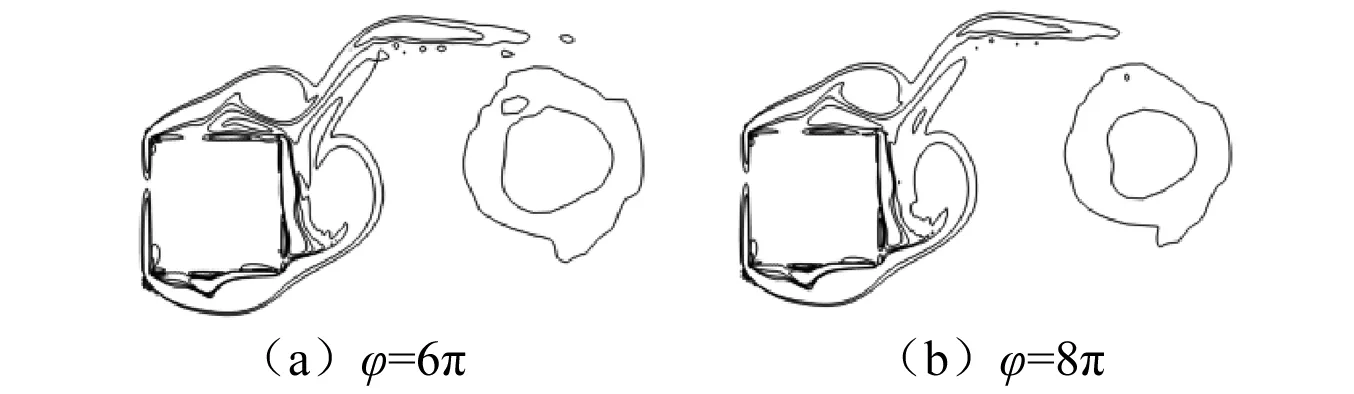
圖13 不同相位振動方柱渦量圖(Stc=0.1)Fig.13 Vortex contour of squares under different phase(Stc=0.1)

Yang等[22]在振動柱體研究中發現，振動物體渦的放出同運動方向密切相關，物體的運動會抑制同方向渦的產生。圖14為本次模擬所得矩形柱不同運動位置處的瞬時渦量圖，當物體向上運動時(圖14(b))，柱體上側壁的流動分離則得到明顯抑制，外形呈帶狀，下側壁流動分離尺寸增大；當物體向下運動時(圖14(c))柱體下方的流動分離得到抑制，被壓成扁平帶狀，上側壁流動分離與零位移位置相比，尺寸增大；零位移位置處(圖14(a))柱體上下表面不再明顯出現上述流動抑制現象。此流動特征隨著柱體振動位置的不同而不斷的轉換，并影響到尾流區渦脫的放出，使渦脫頻率與振動頻率逐漸保持一致。Yang等認為這可能就是造成柱體渦脫頻率同振動頻率鎖定的原因。

圖14 不同運動相位處方柱渦量圖(B/D=1，Stc=0.2)Fig.14 Vortex contour of squares at different oscillating phase (B/D=1，Stc=0.2)

圖15～16為B/D=3，5時，不同運動相位處矩形柱渦量圖。與方柱所得現象相同，柱體表面流動分離特征隨著柱體振動位移的不同而不斷的轉換，并影響到尾流區渦脫的放出，使渦脫頻率與振動頻率逐漸保持一致；但由于柱體邊長比的延長，上述流動特征在運動方向上的影響范圍亦會增大，這也可能是渦脫鎖定區隨邊長比變化的原因。

圖15 不同運動相位處渦量圖(B/D=3，Stc=0.2)Fig.15 Vortex contour of rectangular under different oscillating phase(B/D=3，Stc=0.2)

圖16 不同運動相位處渦量圖(B/D=5，Stc=0.2)Fig.16 Vortex contour of rectangular under different oscillating phase(B/D=5，Stc=0.2)

4.3 氣動系數

圖17為強迫振動方柱表面壓力分布曲線，強迫振動頻率Stc=0.04時，由于外界強迫振動的施加，柱后渦脫加強，此時壓強分布表現為較強的吸力，；Stc=0.1時由于柱后尾流流場的轉換，柱后壓強吸力效應減弱；當Stc=0.15時，強迫振動頻率靠近共振鎖定點，柱后壓強發生躍變，柱后吸力效應突然增強；此后隨著外界振動頻率逐漸增強，柱體背部表面壓強發生較大的減弱，Taylor和Vazza指出這是由于高頻振動下，側壁渦脫和柱后渦脫相互干擾，共同作用的原因。

圖17 不同振動頻率下方柱時均表面壓力分布曲線Fig.17 Distribution of mean surface pressure Cp for squares with varying oscillating frequencies

圖18 不同振動頻率下矩形柱時均表面壓力分布曲線(B/D=3，5)Fig.18 Distribution of mean surface pressure Cp for rectangular with varying oscillating frequencies (B/D=3，5)

如圖18所示，與方柱相同，邊長比B/D=3，5時矩形柱在不同強迫振動工況下，迎風面壓力分布曲線基本保持一致；柱體側面壓力分布曲線不再保持均勻分布，出現曲線特征，這可能是由于邊長比增大，柱體側面發生流動分離-再附而決定的；振動頻率越高，柱體側面前緣負壓特征越明顯，其表面壓力曲線分布特征亦同時增強，表明此時柱體側面渦旋尺寸發生改變，流動分離-再附區長度減小。

圖19為矩形柱時均阻力系數隨振動頻率變化曲線。不同邊長比矩形柱阻力系數均在小振動頻率處均呈現先上升再降低的趨勢；在共振鎖定點附近處，阻力系數達到峰值，結合圖17～18可看出，柱體背后表面吸力效應均突然加強，此后阻力系數迅速降低。此現象發生原因，可能在于共振鎖定點之前，柱后旋渦脫落基本呈現平直脫落的特征，渦脫完全再附于柱體背面(圖13)，超出此振動頻率時，方柱近尾跡流場特征再次發生改變，渦脫向柱側角退縮，再附于方柱背面的現象消失(圖14)。

圖19 不同邊長比矩形柱阻力系數隨振動頻率變化規律Fig.19 Variation of drag coefficients for different side ratio rectangular with varying oscillating frequencies

5 結 論

本文利用IBM算法模型，在靜止網格體系中完成豎向強迫振動柱體的繞流模擬。文章通過設置不同的柱體邊長比，從旋渦脫落、流場特征、氣動系數等方面入手，探究邊長比效應對振動柱體氣動特性的影響：

(1)柱體鎖定區隨邊長比的增大而發生變化，在柱體邊長比為3時，鎖定區出現多級鎖定現象，邊長比升高至5時，柱體鎖定區延長。

(2)柱體運動會抑制同方向渦的產生，并影響到尾流區渦脫的放出；柱體邊長比增大后，柱后尾流渦脫影響范圍變大，這也可能是不同邊長比柱體鎖定區發生變化的原因。

(3)邊長比B/D=3，5時，矩形柱側面壓力分布曲線不再保持均勻分布，出現曲線特征；振動頻率越高，柱體側面前緣負壓特征越明顯，其表面壓力曲線分布特征亦同時增強，表明此時柱體側面渦旋尺寸發生改變，流動分離-再附區長度減小；振動工況下，不同邊長比柱體阻力系數均在接近自然渦脫頻率處(共振鎖定點)發生峰值效應。

在此研究基礎之上，后期將開展典型橋梁斷面的振動繞流數值模擬，利用IBM數值程序的便捷性，增加計算風工程對實際結構的氣動特性研究。