高靈敏度的量子邁克耳孫干涉儀?

左小杰 孫潁榕 閆智輝2) 賈曉軍2)

1)(山西大學光電研究所,量子光學與光量子器件國家重點實驗室,太原 030006)

2)(山西大學,極端光學協同創新中心,太原 030006)

邁克耳孫干涉儀不僅可以用來研究物理學的基本問題,而且能夠用于精密測量,比如引力波信號的測量.因此,構建高靈敏度的邁克耳孫干涉儀是實現微弱信號測量的關鍵.目前,人們利用壓縮態可以降低邁克耳孫干涉儀的噪聲;通過光學四波混頻過程能夠放大馬赫·曾德爾干涉儀中的相位信號,從而提高干涉儀的信噪比和靈敏度.本文研究了一種用于高靈敏度相位測量的量子邁克耳孫干涉儀.在邁克耳孫干涉儀中,利用非簡并光學參量放大器取代干涉儀中的線性光學分束器;并且將壓縮態注入干涉儀的真空通道,可以得到高信噪比和高靈敏度的干涉儀.由于存在不可避免的光學損耗,分析了邁克耳孫干涉儀內部和外部的損耗對相位測量靈敏度的影響.通過理論計算研究了干涉儀的相位測量靈敏度隨系統參數的變化關系,得到了高靈敏度的相位測量量子邁克耳孫干涉儀的實現條件,為用于精密測量的干涉儀的設計提供了直接參考.

1 引 言

1916年,愛因斯坦在廣義相對論中首次預言了引力波的存在[1].最近理論研究表明在雙星系統中可以產生引力波信號[2?5],并且多個國家已開展了引力波直接觀測的研究[6?12].2015年,LIGO中位于美國華盛頓州的Hanford和路易斯安那州的Livingston的兩個探測器在35—250 Hz的頻率范圍內同時觀測到了黑洞雙星系統產生的引力波信號[13];2017年,Advanced LIGO和Advanced Virgo的探測器觀測到了在雙中子星系統中產生的GW 170817信號[14].目前的引力波觀測儀是利用邁克耳孫干涉儀來實現的.由于邁克耳孫干涉儀的輸出光場對兩臂路徑的相位非常敏感,因此通過測量懸掛在真空中鏡子的距離變化引起的相位變化可以直接觀測微弱的引力波信號.微弱的引力波信號的直接觀測是近來的研究熱點之一,這就需要探索設計用于高靈敏度相位測量的邁克耳孫干涉儀.

目前,許多精密測量的靈敏度都受限于標準量子極限.基于量子技術的精密測量可以提高測量靈敏度[15,16].邁克耳孫干涉儀的相位測量靈敏度與它的信噪比有關,通過減小噪聲和放大信號的手段可以提高它的靈敏度.一方面,通過降低注入邁克耳孫干涉儀的電磁場或者真空的噪聲,可以提高干涉儀的信噪比,進而使其相位測量的靈敏度超越標準量子極限.在用于引力波測量的邁克耳孫干涉儀中,真空起伏進入了干涉儀的反對稱端,限制了相位測量的靈敏度.對于相干態或者真空態,兩個正交分量有相同的不確定性關系,并且不確定性乘積滿足海森伯不確定性關系.由于光場的量子力學本性,光子的散粒噪聲決定了干涉儀臂長在公里尺度的邁克耳孫干涉儀的位移靈敏度極限在艾米量級.對于壓縮態,一個正交分量的起伏低于真空態的起伏(量子噪聲極限),同時,它的共軛正交分量的起伏必將高于真空態的起伏,使其乘積滿足海森伯不等式[17,18].Caves指出利用壓縮態取代真空態可以使其正交分量的起伏低于量子噪聲極限,進而提高干涉儀的相位測量靈敏度[19?21].而且,利用非線性光學介質可以在射頻[22?26]以及音頻[27?29]范圍內產生壓縮態光場,并且可以將其應用于邁克耳孫干涉儀來增強相位測量的靈敏度[30,31].2011年,GEO600探測儀利用在700 Hz處的壓縮態實現了超越標準量子極限的精密相位測量[32];2013年,LIGO探測儀利用壓縮態提高了在150 Hz處的靈敏度,使其超越標準量子極限[33].

另一方面,通過放大邁克耳孫干涉儀的信號,也可以提高干涉儀的信噪比和靈敏度.傳統干涉儀通常利用線性光學分束器實現光場的分束與合束.參量放大過程在量子技術的多個領域有著廣泛的應用[34?36].Yuerke等[37],Plick等[38]分別提出利用參量放大過程實現攜帶相位信息光場的分束與合束,可以放大干涉儀中的相位信號;隨后,Ou[39]將其推廣至相位測量的任意幺正變換.原子系綜是開展量子技術的理想平臺之一[40,41],基于原子系綜的四波混頻過程不僅可以用糾纏產生和操控[42],而且可以用于光場的分束與合束.華東師范大學開展了一系列基于四波混頻的非線性干涉儀的研究[43?48].在馬赫-曾德爾干涉儀中,它們研究了干涉儀的經典和量子性質,將干涉儀的信噪比提高了4.1 dB,并且使相位測量的靈敏度超越了散粒噪聲極限1.6倍[43,44].隨后,他們將線性與非線性技術相結合構建了混合型干涉儀[49].

本文研究了基于非線性分束器和壓縮態填補真空通道技術的量子邁克耳孫干涉儀.光學參量放大器是實現參量放大的有效器件之一,能夠用于實現光學參量放大.我們將非簡并光學參量放大器引入邁克耳孫干涉儀,使其取代干涉儀中的線性分束器,構建基于非簡并光學參量放大器的邁克耳孫干涉儀.通過非簡并光學參量放大器對信號的放大作用,實現了干涉儀信噪比的提高.同時,壓縮態光場填補真空通道的技術可以降低邁克耳孫干涉儀的噪聲水平,進一步提高干涉儀的信噪比.由于不完美光學元件的應用,我們考慮了干涉儀內部和外部的損耗對非線性邁克耳孫干涉儀的相位測量靈敏度的影響.根據非簡并光學參量放大器和邁克耳孫干涉儀的理論模型,分析了相位測量靈敏度和干涉儀內相敏光場強度、非簡并光學參量放大器的參量放大因子、注入壓縮態的壓縮參量、干涉儀內部和外部的損耗等實驗參數的關系,得到了高靈敏度的量子邁克耳孫干涉儀的實現條件.在合適的參數下,該量子邁克耳孫干涉儀的相位測量靈敏度可以優于標準量子極限,為高靈敏度的邁克耳孫干涉儀的實驗實現提供了理論依據.

2 理論模型

線性和基于非簡并光學參量放大器的邁克耳孫干涉儀的原理圖分別如圖1(a)和圖1(b)所示.

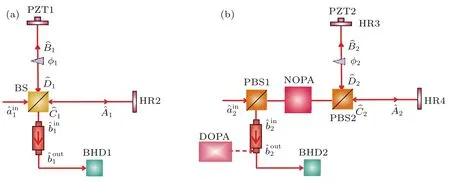
圖1 (a)線性邁克耳孫干涉儀;(b)基于非簡并光學參量放大器的量子邁克耳孫干涉儀;BS,光學分束器;PBS1,偏振分束棱鏡1;PBS2,偏振分束棱鏡2;NOPA,非簡并光學參量放大器;DOPA,簡并光學參量放大器;BHD 1,平衡零拍探測器1;BHD 2,平衡零拍探測器2Fig.1.(a)Linear Michelson interferometer;(b)OPA based quantum Michelson interferometer.BS,beam splitter;PBS1,polarization beam splitter1;PBS2,polarization beam splitter2;NOPA,non-degenerated optical parametric amplifier;DOPA,degenerated optical parametric amplifier;BHD 1,balanced homodyne detector1;BHD 2,balanced homodyne detector 2.

2.1 線性邁克耳孫干涉儀的理論模型

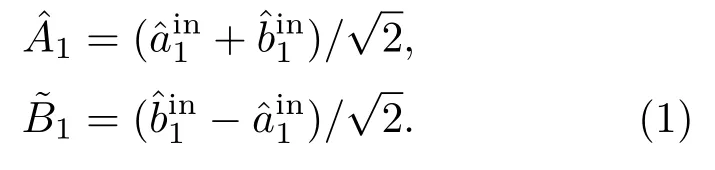
由于存在不可避免的光學損耗,干涉儀內部的光學損耗L1被考慮在理論模型中.經0?高反鏡HR1和HR2反射后光場和分別為:

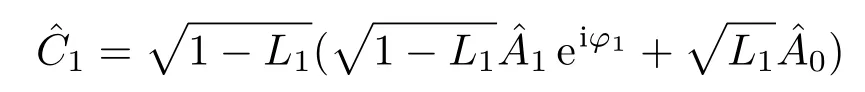
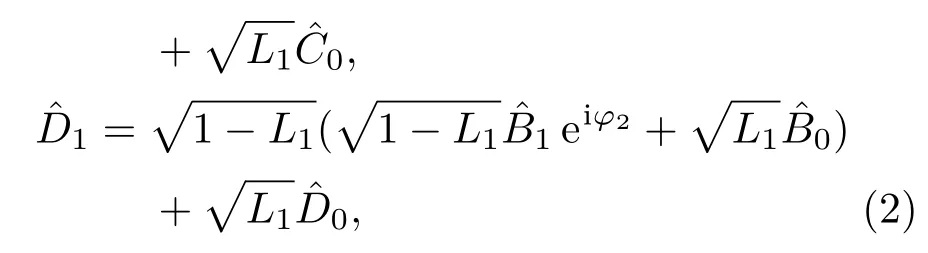
式中,φ1,φ2是每一臂的相位;干涉儀兩臂之間的相位差為?1=φ1?φ2.假設每個干涉儀臂上的光學損耗都相同為為由于光學損耗L1引入的真空噪聲.

考慮干涉儀外部的光學損耗L2,干涉儀輸出光場為

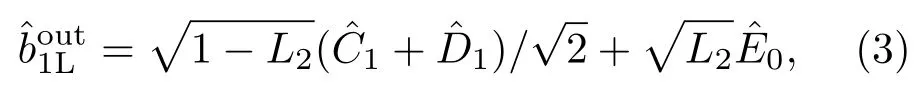
當?=2kπ時,假設測量的相位靈敏度為δ(δ?1),我們可以得到線性邁克耳孫干涉儀輸出光場的正交相位分量為

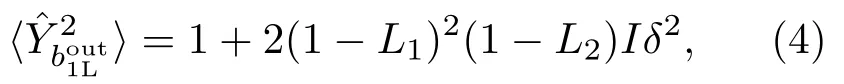
這里,干涉儀內相敏光場強度為I=|α|2/2,α為注入干涉儀的光子數,|α|2?1.

由此可得線性邁克耳孫干涉儀的信噪比為

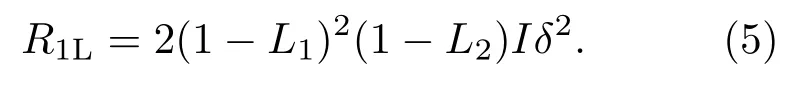
靈敏度是描述精密測量的重要指標.光學干涉儀的靈敏度受限于光子的散粒噪聲,通過經典的重復測量方法不能消除這部分噪聲,相應的測量靈敏度被稱之為標準量子極限這里N是重復測量的次數.

根據干涉儀的信噪比(5)式,可以得到相位測量的靈敏度為

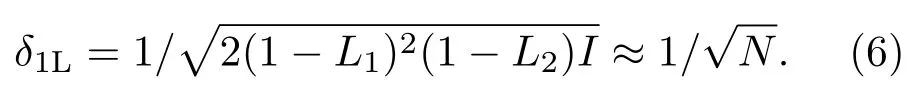
因此,線性邁克耳孫干涉儀的靈敏度可以當作標準量子極限.

如果用壓縮態填補邁克耳孫干涉儀的真空通道,可以提高干涉儀的信噪比和靈敏度.若端注入為壓縮真空態,其中,r為注入壓縮態的壓縮參量.根據正交分量的定義,線性邁克耳孫干涉儀輸出光場的正交相位分量為

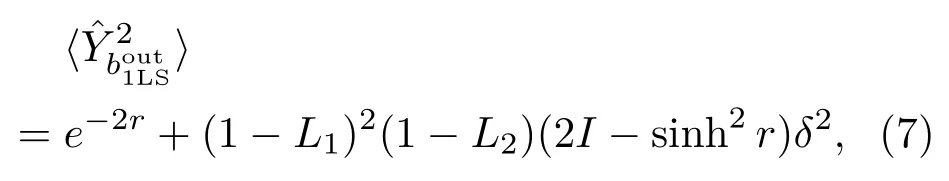
其中,干涉儀內相敏光場強度為I=(|α|2+sinh2r)/2.

于是,壓縮態注入的線性邁克耳孫干涉儀的信噪比為

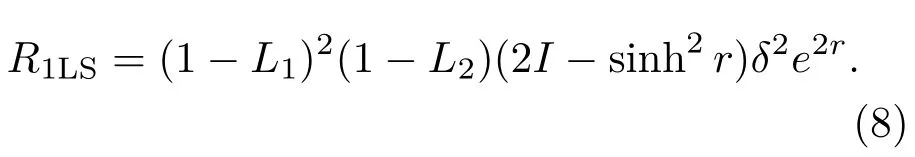
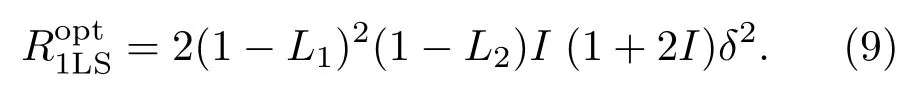
相應的最佳相位測量靈敏度為

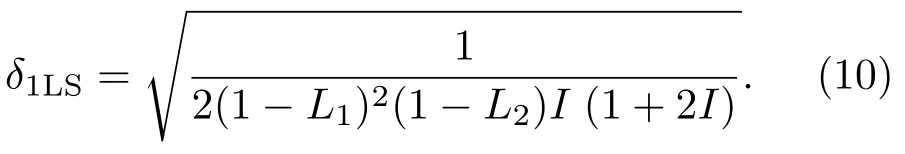
2.2 量子邁克耳孫干涉儀的理論模型

光學參量放大器通過光學諧振腔有效地增強了光學參量下轉換過程,是制備非經典光場的有效器件之一.非簡并光學參量放大器通常用參量增益模型來描述,相應的哈密頓量為

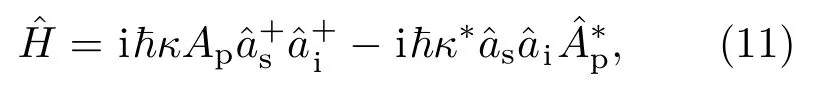
在非線性的邁克耳孫干涉儀中,分束與合束的元件不再是線性分束器,取而代之的是非簡并光學參量放大器系統.該非簡并光學參量放大器系統的輸入輸出關系如下:

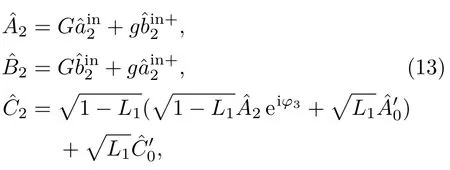
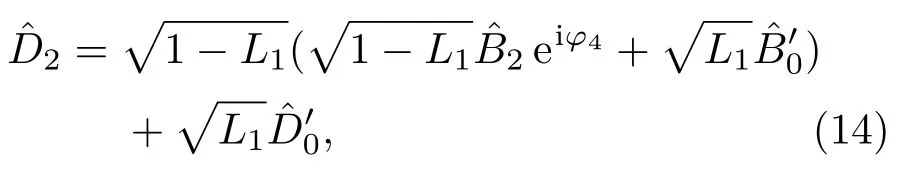
式中,φ3,φ4是每一臂的相位;干涉儀兩臂之間的相位差為?2=φ3?φ4;L1為干涉儀內部的光學損耗;為干涉儀內部的光學損耗L1引入的真空噪聲.

非線性邁克耳孫干涉儀的輸出光場為

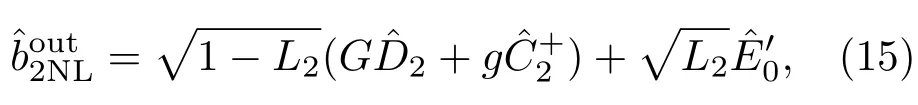
式中,L2為干涉儀外部的光學損耗,為干涉儀外部的光學損耗L2引入的真空噪聲.

當?2=π+2kπ時,正交相位分量為

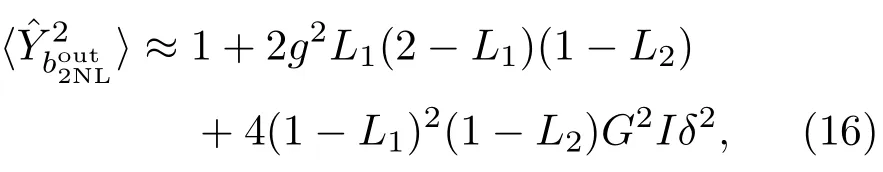
其中相敏光場強度為I≈g2|α|2.

因此非線性邁克耳孫干涉儀的信噪比為

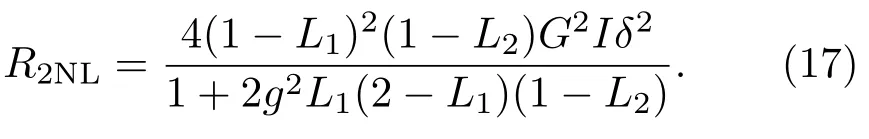
相應的相位測量的靈敏度為

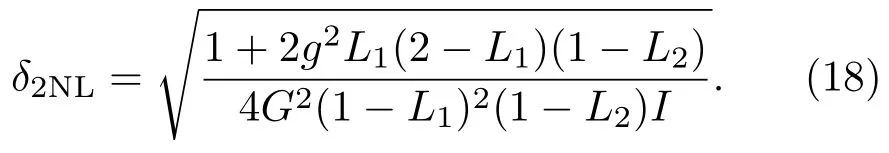
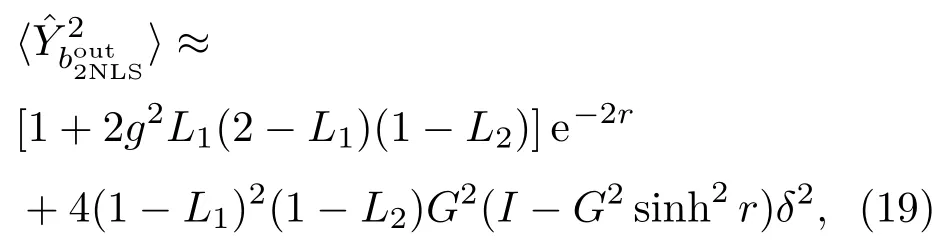
因此,非線性邁克耳孫干涉儀的信噪比為

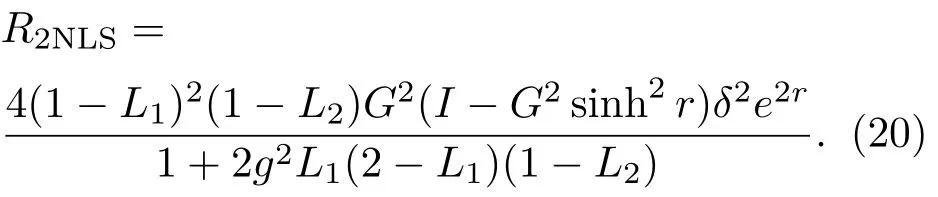
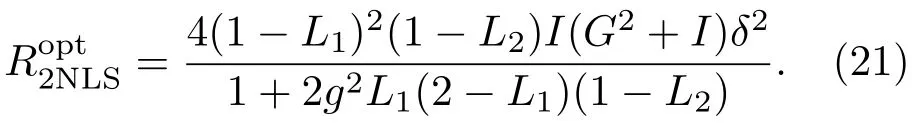
相應的最佳相位測量的靈敏度為

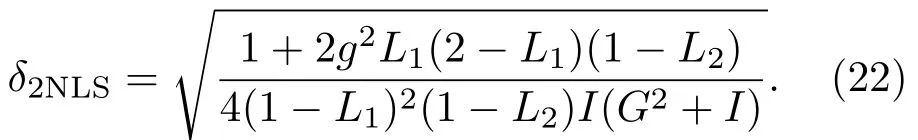
3 理論結果與分析

接下來,我們分析注入壓縮態的壓縮度、邁克耳孫干涉儀內相敏光場強度、非簡并光學參量放大器增益因子、邁克耳孫干涉儀內部以及外部損耗等因素分別對量子邁克耳孫干涉儀的影響.

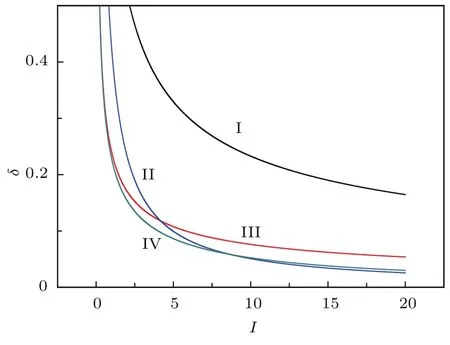
圖2 邁克耳孫干涉儀的靈敏度隨干涉儀內部相敏光場強度的變化Fig.2.The function of the sensitivity of Michelson interferometer on phase sensing field insensity for phasing sensing inside interferometer.

圖2 描述了邁克耳孫干涉儀的靈敏度隨干涉儀內部相敏光場強度的變化關系.圖中,曲線I(黑色)、曲線II(藍色)、曲線III(紅色)、曲線IV(綠色)分別對應于無壓縮態注入的線性邁克耳孫干涉儀(根據(6)式可以近似作為標準量子極限)、壓縮態注入的線性邁克耳孫干涉儀、無壓縮態注入的非線性邁克耳孫干涉儀、壓縮態注入的非線性邁克耳孫干涉儀的相位測量靈敏度.非簡并光學參量放大器的增益因子取G=3,干涉儀內部和外部的光學損耗分別為L1=0.03和L2=0.02.從圖中可以看出各種干涉儀的靈敏度都隨相敏光場強度的增加而變好.注入壓縮態的邁克耳孫干涉儀和非線性邁克耳孫干涉儀,均可以提高相位測量的靈敏度,使其遠低于標準量子極限.在相敏光場的強度小于4.17時,無壓縮態注入的非線性邁克耳孫干涉儀比起壓縮態注入的線性干涉儀有更好的相位測量靈敏度;當相敏光場的強度大于4.17時,壓縮態注入的線性邁克耳孫干涉儀比起無壓縮態注入的非線性邁克耳孫干涉儀有更好的靈敏度;當相敏光場的強度較弱時(小于8.68),壓縮態注入的非線性邁克耳孫干涉儀比起壓縮態注入的線性干涉儀有更好的相位測量靈敏度,達到量子干涉儀最佳相位測量靈敏度;當相敏光場的強度較大時(大于8.68),壓縮態注入的線性邁克耳孫干涉儀接近壓縮態注入的非線性干涉儀的靈敏度,均可以達到量子干涉儀最佳相位測量靈敏度.因此,壓縮態注入的非線性邁克耳孫干涉儀適用于微弱信號的精密測量;在相敏光場強度較大的情況下,壓縮態注入的線性邁克耳孫干涉儀可以達到最佳相位測量靈敏度.

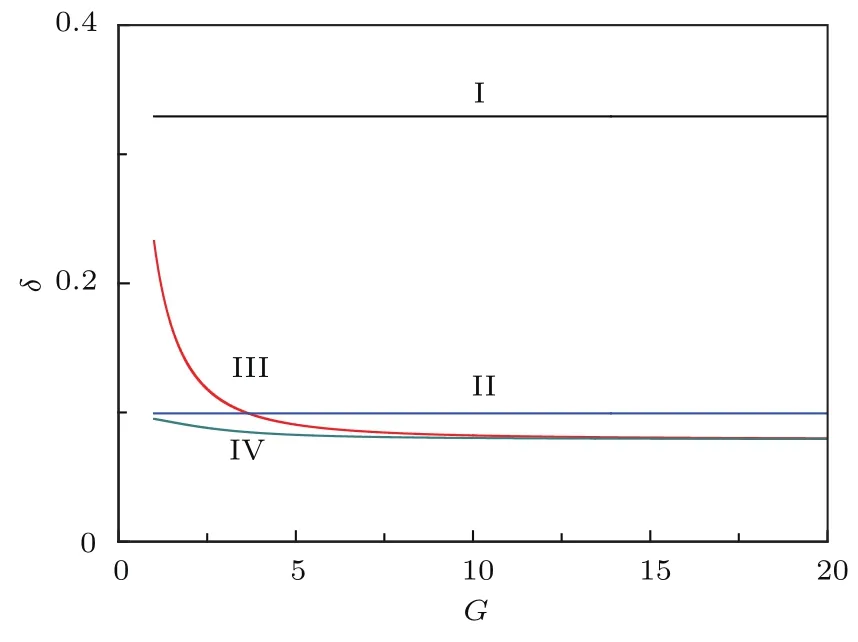
圖3 邁克耳孫干涉儀的靈敏度隨光學參量放大器增益因子的變化Fig.3.The function of the sensitivity of Michelson interferometer on gain factor of optical parametric amplifier.

圖3 描述了邁克耳孫干涉儀的靈敏度隨光學參量放大器增益因子的變化關系,曲線I(黑色)、曲線II(藍色)、曲線III(紅色)、曲線IV(綠色)的定義以及其他系統參數與圖2相同.邁克耳孫干涉儀中其他參數選擇如下:干涉儀內部相敏光場強度取I=5,干涉儀內部和外部的光學損耗分別為L1=0.03和L2=0.02.從圖中,可以得出干涉儀的靈敏度隨著非簡并光學參量放大器增益因子的增加而提高.非簡并光學參量放大器的引入、壓縮態注入的技術都能夠使相位測量的靈敏度優于標準量子極限.在增益因子小于3.66時,與無壓縮態注入的非線性干涉儀相比較,壓縮態注入的線性邁克耳孫干涉儀有更好的相位測量靈敏度;當增益因子大于3.66時,與壓縮注入的線性邁克耳孫干涉儀相比較,無壓縮態注入的非線性邁克耳孫干涉儀有更好的靈敏度;當增益因子較弱時(小于13),壓縮態注入的非線性邁克耳孫干涉儀達到量子干涉儀最佳相位測量靈敏度;當增益因子較大時(大于13),無壓縮態注入的非線性邁克耳孫干涉儀接近壓縮態注入的非線性干涉儀的靈敏度,均可以達到量子干涉儀最佳相位測量靈敏度.因此,光學參量放大器的引入可以節約量子資源——壓縮態.隨著增益因子的提高,需要注入的壓縮態的壓縮度降低.當增益因子G=3時,線性邁克耳孫干涉儀需要注入?13 dB的壓縮態(對應的最佳壓縮參量為1.52),非線性邁克耳孫干涉儀僅需要注入?4 dB的壓縮態(對應的最佳壓縮參量為0.45);甚至當增益因子達到一定條件時,可以不需要注入壓縮態而達到最佳靈敏度.

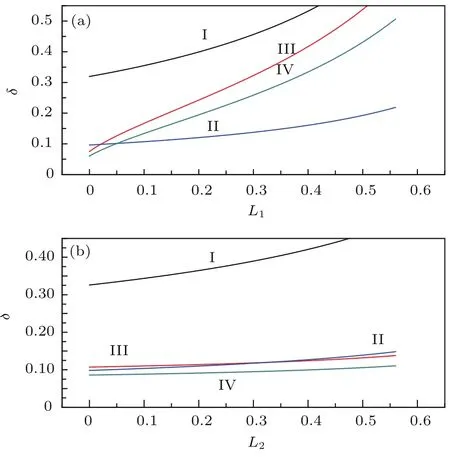
圖4 邁克耳孫干涉儀的靈敏度隨干涉儀損耗的變化 (a)干涉儀內部損耗;(b)干涉儀外部損耗Fig.4.The function of the sensitivity of Michelson interferometer on loss inside(a)the loss in the interferometer;(b)the loss outside the interferometer.

圖4 (a)和圖4(b)分別描述了邁克耳孫干涉儀的靈敏度隨干涉儀內部損耗和外部損耗的變化關系,曲線I(黑色)、曲線II(藍色)、曲線III(紅色)、曲線IV(綠色)的定義以及其他系統參數與圖2相同.邁克耳孫干涉儀中其他參數選擇如下:非簡并光學參量放大器的增益因子取G=3,干涉儀內部相敏光場強度取I=5,圖4(a)中干涉儀外部的光學損耗為L2=0.02,圖4(b)中干涉儀內部的光學損耗為L1=0.03.從邁克耳孫干涉儀的靈敏度隨干涉儀內部損耗和外部損耗的變化關系中,我們可以看出邁克耳孫干涉儀的靈敏度隨干涉儀內部、外部損耗的增加而變差.通過減小系統的損耗,特別是干涉儀內部損耗,可以顯著提高相位測量的靈敏度.與無壓縮態注入的線性邁克耳孫干涉儀相比較,三種量子干涉儀的靈敏度受干涉儀外部損耗的影響都不敏感.在較小的邁克耳孫干涉儀內部損耗的情況下(小于0.05),非線性干涉儀有更好的靈敏度.當邁克耳孫干涉儀內部損耗大于0.05時,壓縮態注入的線性邁克耳孫干涉儀的靈敏度好于非線性邁克耳孫干涉儀的靈敏度.非線性邁克耳孫干涉儀對內部損耗較為敏感,適用于低干涉儀內部損耗的情況;在較大的干涉儀內部損耗的情況下,壓縮態注入的線性邁克耳孫干涉儀仍有較好的相位測量靈敏度,具有很好的精密測量穩定性.

由上面的理論分析可知,量子邁克耳孫干涉儀的靈敏度在很大的參數范圍內可以超越標準量子極限.由于光學參量放大器輸出光場的量子噪聲之間存在關聯,因此,當它們再次耦合時,相消干涉可以減小相互關聯的量子噪聲,放大包含相位信息的信號,從而提高干涉儀的信噪比和靈敏度.并且,注入壓縮態可以進一步降低干涉儀的量子噪聲,對于壓縮態注入的非線性邁克耳孫干涉儀,非簡并光學參量放大器的增益因子取G=3,干涉儀內相敏光場取I=5,干涉儀內部和外部的光學損耗分別為L1=0.03和L2=0.02,注入壓縮態的最佳壓縮參量為0.45,相應的最佳相位測量靈敏度可以達到0.09.三種量子邁克耳孫干涉儀適用于不同的條件.由上面的理論分析可知,不同量子邁克耳孫干涉儀的靈敏度在很大的參數范圍內可以超越標準量子極限.由于光學參量放大器輸出光場的量子噪聲之間存在關聯,因此,當它們再次耦合時,相消干涉可以減小相互關聯的量子噪聲,放大包含相位信息的信號,從而提高干涉儀的信噪比和靈敏度.并且,注入壓縮態可以降低干涉儀的量子噪聲.在一定條件下,非線性邁克耳孫干涉儀和注入壓縮態的線性干涉儀可以分別接近最佳相位測量靈敏度.壓縮態注入的非線性邁克耳孫干涉儀適用于微弱信號的精密測量,并且能夠降低注入壓縮態的壓縮度.壓縮態注入的線性邁克耳孫干涉儀在相敏光場強度較大的情況下,可以達到最佳相位測量靈敏度,并且對干涉儀內部損耗更加不敏感.

4 結 論

非線性邁克耳孫干涉儀與壓縮真空態填補邁克耳孫干涉儀真空通道的技術都可以提高干涉儀的靈敏度,我們通過對基于這兩種技術的邁克耳孫干涉儀靈敏度隨系統參數變化的依賴關系的理論計算,比較了三種量子邁克耳孫干涉儀,得到了它們的適用條件及優勢.在很大的參數選擇范圍內,量子邁克耳孫干涉儀的靈敏度可以超越標準量子極限.在微弱信號精密測量中,壓縮態注入的非線性邁克耳孫干涉儀具有最佳的靈敏度,并且可以節約量子資源——壓縮態.壓縮態注入的線性邁克耳孫干涉儀對于較大相敏強度信號的測量可以達到與壓縮態注入的非線性邁克耳孫干涉儀相同的靈敏度,并且具有良好的靈敏度穩定性.本文的研究為高信噪比和靈敏度的干涉儀的實驗實現提供了理論參考.