基于回歸模型的辦公建筑距高比與燈具類型的關系

肖 輝，陸正飛

(同濟大學電子與信息工程學院，上海 201804)

引言

建筑照明設計是建筑電氣工程設計的重要內容之一。在實際工程設計中，不同的層高有其相應的配光曲線燈具。若忽略此問題，將會導致照度或者功率密度達不到國家標準或規范的要求值。目前的照明設計實況中，設計師幾乎都是將照度和功率密度分為兩步來考慮，程序比較復雜。

《建筑照明設計標準》(GB 50034—2013)[1]中對于不同場所推薦了相應的照明燈具。在實際的工程設計中，很多情況下燈具的型號是唯一確定的，對于設計師而言其照明配光曲線已經相應的確定下來[2]。然而，要明確給定的燈具是否能同時符合照度與功率密度兩大要求這一問題，設計師通常是先按照度值進行設計，設計好后再按功率密度值進行校驗，若功率密度不符合要求，則調整距高比[3]重新設計后再次校驗，以此循環往復。但是，在實際中很多燈具在特定的場合內是無法適用的，這就給照明設計師帶來了很多繁瑣而無用的工作[4]。

本文首先從數學推導的角度出發，將照度與功率密度兩個條件合并為一個條件即利用系數；其次通過仿真實驗，通過回歸算法分析在特定類型建筑中，給定的燈具及配光曲線能否能同時滿足照度和功率密度兩個要求，給出普遍適用的分析方法；最后得出給定類型的燈具能同時滿足照度與功率密度時的距高比的范圍值。通過以上兩個問題的分析研究，為照明設計人員提供一定的參考。

1 參數的確定

照明功率密度(LPD)與利用系數法的公式如下：

(1)

(2)

聯合(1)、(2)式推導得

即

(3)

其中Eav為平均照度，Φ為光通量，U為利用系數，k為維護系數，LPD為功率密度，P為每套燈具的功率。

根據GB 50034—2013中的規定，照度標準值以及照明功率密度限值如表1所示。

表1 辦公建筑或者具有建筑中具有辦公用途場所照明功率密度限值

在辦公建筑中，根據表1取值E=300 lx，LPD現行值為15.0。

因此，辦公建筑的維護系數k取值為0.80(如表2所示)。

按照GB 50034—2013《建筑照明設計標準》對于照度均勻度的規定，公共建筑的工作房間和工業建筑作業區域內一般照明的照度均勻度不應小于0.7，而作業面鄰近周圍的照度均勻度不應小于0.5(如表3所示)。

表2 照明維護系數表

表3 辦公建筑照明標準值

2 回歸算法

通過以上的分析可知，光通量、維護系數k、每套燈具的功率P可以通過相應的規范查得，是一個定值；平均照度Eav，功率密度LPD為區間值。

利用系數U與燈具規格、安裝高度、墻面材料、房間結構等幾大因素有關。由于墻面材料和房間結構不是電氣所涉及的部分，這里不做太多的討論。以下主要對利用系數U與燈具規格和等級安裝高度的關系進行研究。因此可以選擇利用系數和安裝高度進行回歸分析。

用已知樣本對未知公式參數的估計，給出一個點集D，用一個函數去擬合這個點集，并且使得點集與擬合函數間的誤差最小。如果這個函數曲線是一條直線，那就被稱為線性回歸；如果曲線是一條二次曲線，就被稱為二次回歸[5]。

假定預測值與樣本特征間的函數關系是線性的，回歸分析的任務，就在于根據樣本X和Y的觀察值去估計函數h，尋求變量之間近似的函數關系。定義hθ(x)=θ0+θ1x1+θ2x2+θ3x3+…+θnxn，其中n為特征數目；為了方便，記x0=1，則多變量線性回歸可以記為

hθ(x)=θTx

(4)

線性回歸的求解方法很多，比如梯度下降法、普通最小二乘法、局部加權線性回歸、嶺回歸等，本文主要用的是最普遍的普通最小二乘法。

本文主要討論不同的燈具的安裝高度對于利用系數的影響的數學研究方法，所以在DAILux仿真環節實驗次數不多。通過Python的類庫sklearn下的linear_model中有封裝好的LinearRegression方法[6]。

燈具光通量與燈具的功率P是根據特定的燈具類型決定的。

3 仿真分析

本文選用幾組常用的燈具，給定某個特定的場景，通過DAILux仿真，通過控制燈具布置高度得出相應的利用系數。根據仿真得到的多組數據，用數學算法得出相應的擬合函數。

1)場景設置。選取普遍化的辦公空間，長為12 m，寬為10 m，毛坯房高度為4.2 m，工作面高度為0.75 m。房間各平面的反射比為天花板70%，墻壁50%，地板20%，維護系數為0.80。出于對照度均勻度以及眩光等因素的考慮，燈具采用均勻布置方式，高度不低于2.8 m。

2)DIALux仿真。根據利用系數的定義，可以方便得知利用系數可以由工作面的光通量與光源出射光通量的比得到[7]。

DIALux仿真中沒有利用系數這一指標[8]，但有平均照度和燈具總光通量，通過這兩組數據可以得到利用系數，可以得到如下幾組數據。

(a)第一組實驗。燈具型號如圖1所示。

圖1 Philips T8熒光燈的參數Fig.1 The parameters of the Philips T8 fluorescent lamp

我們選擇的燈具是Philips 熒光燈功率為72 W，光通量為6 500 m的燈具。由圖1與式(3)可知，利用系數的取值范圍為[0.447 5,1]。利用系數U≥0.447 5時，同時滿足照度以及功率密度要求,若利用系數U不在此范圍內，則不能滿足設計標準。根據仿真實驗，作業面鄰近周圍的照度均勻度為0.54>(0.5),因此滿足要求(仿真數據如表4所示)。擬合曲線如圖2所示，其中橫坐標為高度，縱坐標為利用系數。其線性回歸方程為

y=-0.048 6x+0.559 6

(5)

此處需要滿足利用系數U≥0.447 5，即y≥0.447 5,則可以得到x≤2.3 m。顯然，x為燈具的安裝高度，因此該燈具在不能同時滿足照度與功率密度的要求。

由此可見，該燈具在一般安裝高度即2.8 m～4.0 m之間均不能同時滿足照度與功率密度需求。

(b)選取第二組數據進行仿真實驗。燈具型號如圖3所示。第二組是歐普的燈具，功率為108 W、光通量為6 303 lm的燈具。

表4 第一組實驗DIALux仿真數據

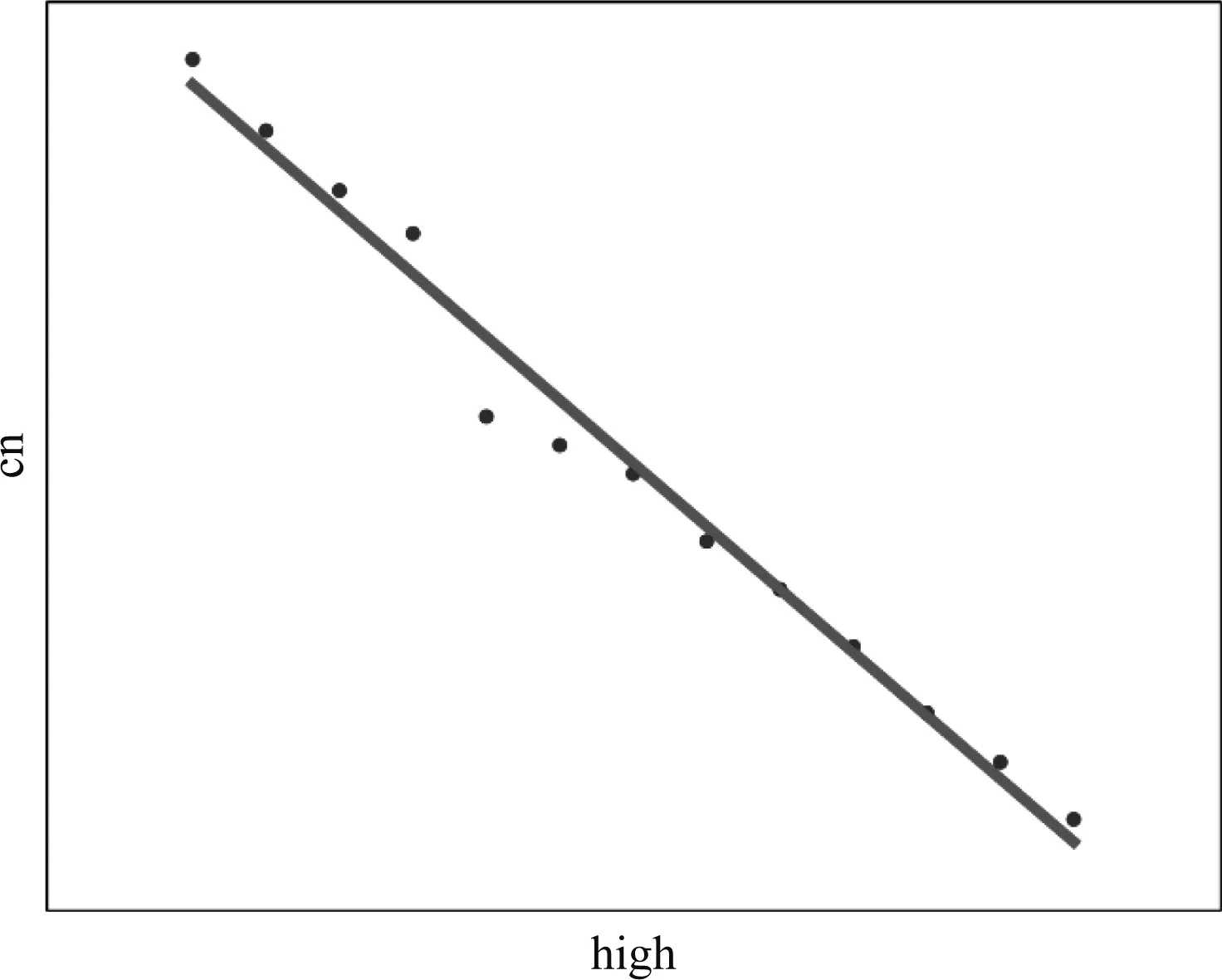
圖2 第一組實驗的線性回歸擬合圖Fig.2 Linear regression fitting of the first experiment

根據公式(3)，得到利用系數U的取值范圍 [0.447 5,1]，根據Dialux仿真得到表5數據。擬合曲線圖如圖4所示。

其線性回歸方程為

y=-0.057 401 1x+0.505 75

(6)

此處需要滿足利用系數U≥0.461 5，即y≥ 0.461,則可以得到x≤4.127 6。顯然，x為燈具的安裝高度，因此該燈具在辦公建筑中基本都可以滿足要求。

圖3 歐普燈具參數Fig.3 The parameters of the Opple lamp

由此可見，該燈具在制定高度下滿足照度與功率密度的要求。在滿足照度以及功率密度的前提下，最適宜安裝高度為4.1 m以下位置按需選擇。

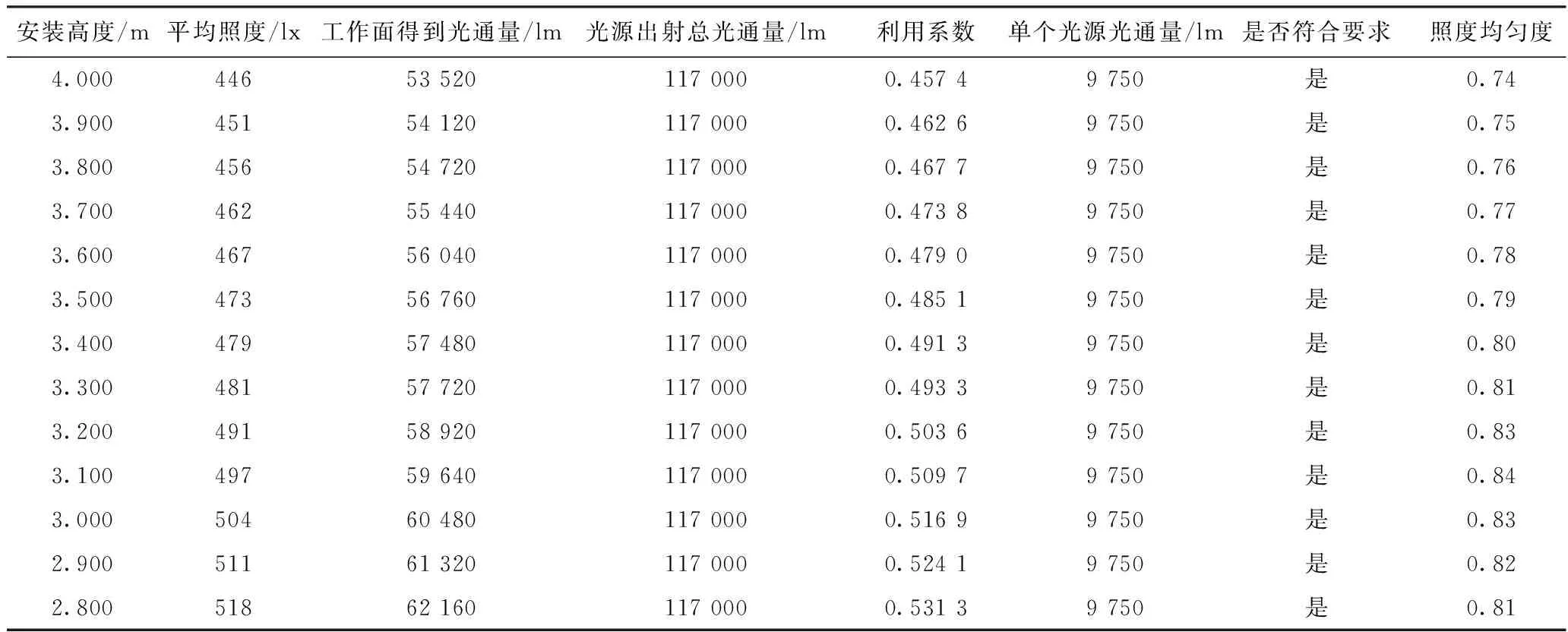
表5 第二組實驗Dialux仿真數據

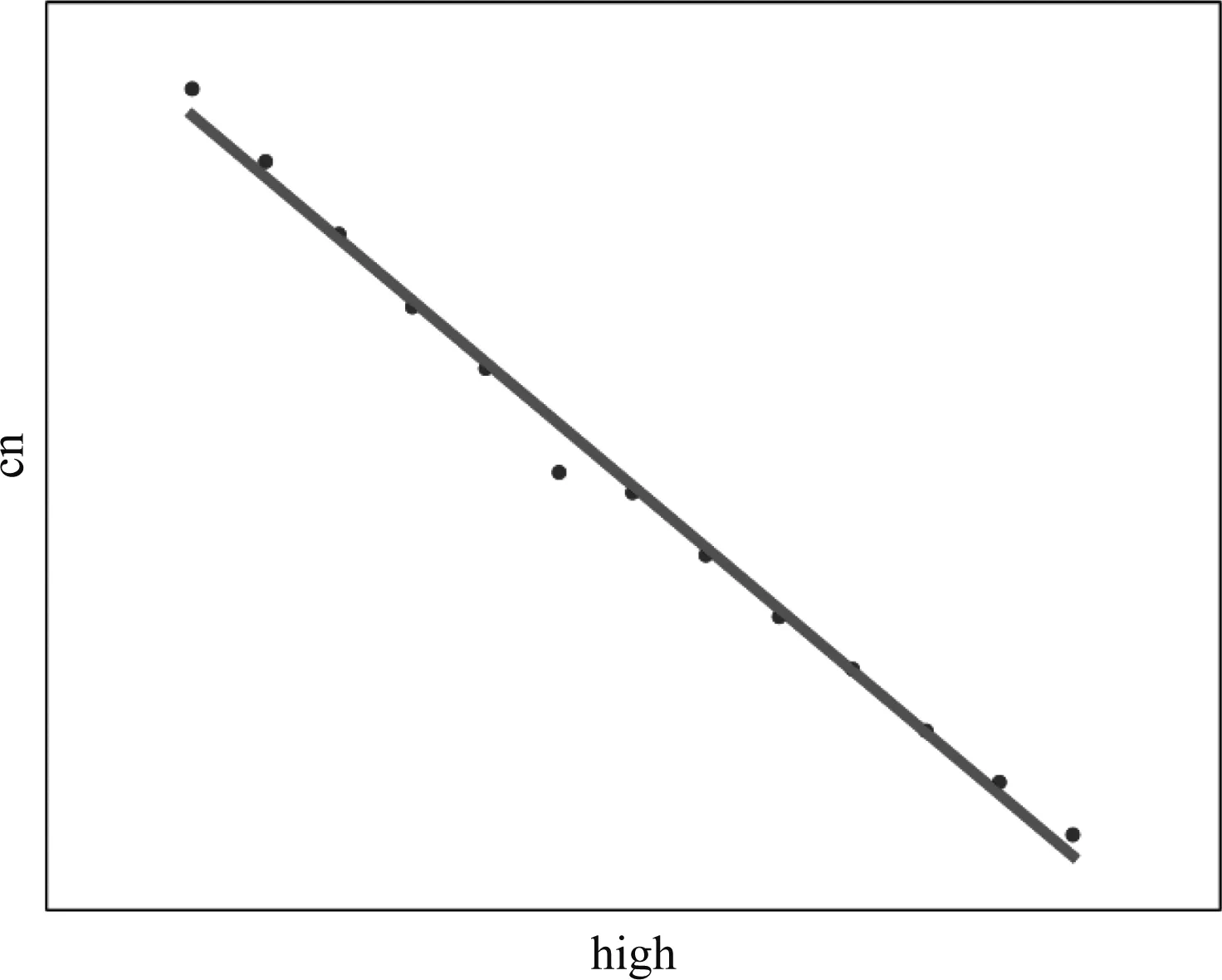
圖4 第二組實驗的線性回歸擬合圖Fig.4 Linear regression fitting of the second experiment

4 結束語

我們對照度公式以及功率密度公式進行數學推導，查找相應的規范，將兩大變量改為一個利用系數變量，并且找出同時滿足照度與功率密度時所對應的利用系數的區間范圍。通過DIALux軟件仿真得到仿真數據，綜合運用回歸算法，求得相應的利用系數與燈具及距高比的數學關系。以此為依據，判斷在某特定空間下某種特定燈具能否適用于該環境，并且給出某特定燈具滿足照度與功率密度時需要符合的距高比范圍。