驅動微梁梁寬誤差對微陀螺性能的影響*

郝淑英， 李會杰， 齊成坤， 張辰卿， 陳 煒， 馮晶晶

(1. 天津理工大學 機械工程學院，天津 300384;2.天津市先進機電系統設計與智能控制重點實驗室，天津 300384)

0 引 言

加工誤差會嚴重影響微陀螺的性能，改變微陀螺的固有頻率、帶寬、靈敏度，影響微陀螺系統輸出的精度及穩定性[1～2]。施芹等人[3]對彈性不等、阻尼不對稱等問題進行研究并優化結構，降低了機械耦合誤差，提高了零偏穩定性[4]。鄭怡文等人[5]全面分析了正交誤差產生的主要因素，并論述了如何減小加工誤差帶來的正交誤差。劉學等人[6]提出一種正交誤差閉環控制自補償方法，降低了正交誤差。賀琨等人[7]得出振動結構支撐梁的加工誤差是引起結構剛度不對稱并產生模態耦合誤差的主要因素，并采用紫外激光微細加工技術，對微陀螺樣機進行了結構平衡實驗，降低了樣機模態耦合誤差信號峰值。Lü B[8]得出只有一根驅動梁梁寬有加工誤差時，驅動模態運動不同于理想時的運動。上述研究充分揭示了微梁加工誤差對模態耦合及輸出信號的影響是進行補償和修正的前題，但多為定性的理論分析。

本文以一種驅動質量塊在外、檢測質量塊在內的梳狀微陀螺為研究對象[9]，采用有限元分析方法研究了3類典型的微梁梁寬，10種加工誤差對微陀螺驅動和檢測模態固有頻率和模態的影響，對模態耦合的特征及產生的條件進行了定量分析。針對微陀螺輸入的交變電壓信號特性(類似于簡諧激勵)和微結構實驗的高成本和復雜性，采用有限元仿真的方法，通過施加簡諧激勵模擬微陀螺輸入的電信號，研究了無角速度輸入情況下各類加工誤差對微陀螺檢測信號的影響。

1 梳狀微陀螺的有限元模型驗證

為了降低直彈性梁對微陀螺帶來的不利影響，在保持微梁剛度不變的條件下，設計了驅動微梁為U型梁和檢測微梁為蟹腳型梁的微陀螺模型，改進了文獻[10]的微陀螺微梁的模型，改進后的模型如圖1所示。選擇Solid195單元，采用多晶硅材料參數，其密度ρ=2.33×103kg/m3，泊松比μ=2.78，彈性模量E=169 GPa,共劃分了38 478個單元，其有限元模型如圖2所示，微陀螺驅動部分的等效質量為mx=2.007×10-9，檢測模態的等效質量為my=0.907×10-9kg。有限元模態分析結果驅動模態固有頻率ωd=29.64 kHz，檢測模態固有頻率ωs=29.90 kHz。

圖1 梳狀微陀螺儀模型

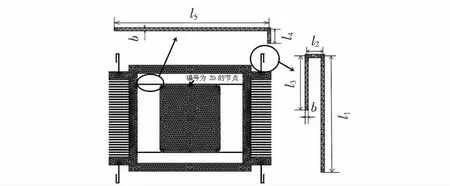
圖2 微陀螺有限元分析模型

圖2中局部放大圖為U形驅動梁和蟹腳檢測梁的有限元模型，采用能量法求出二者檢測方向的剛度表達式為[11]

(1)

驅動模態和檢測模態的固有頻率為

(2)

由式(2)計算得驅動模態和檢測模態對應的固有頻率值為30.30，30.49 kHz;與有限元結果比較得，驅動模態固有頻率誤差為2.18 %，檢測模態固有頻率誤差為1.94 %，由此，驗證有限元模型的可靠性。

2 微梁寬度誤差對微陀螺固有頻率和模態的影響

設Δi(i=1,2,3,4)為驅動微梁梁寬的相對誤差。驅動微梁的彈性剛度與慣性矩成正比，是梁寬b的3次方，當Δ很小時，可忽略Δ的高次項，則剛度變化了3Δ。因此微陀螺驅動方向的剛度矩陣[12]可表示為

(3)

式中kxx,kyy,kθθ分別為x,y,z軸的剛度，kxy,kxθ,kyθ分別為x軸和y軸，x軸和繞z軸，y軸和繞z軸之間的耦合剛度。由式(3)可知當微陀螺處于理想加工狀態，即驅動微梁梁寬的相對誤差Δi為零時，剛度矩陣非對角線元素均為零，此時微陀螺不會出現正交耦合誤差。當微梁寬度存在加工誤差時，剛度矩陣非對角線元素不全為零，此時微陀螺存在正交耦合誤差。單根支撐梁的梁寬加工誤差一般為0.1～0.2 μm[3]。

根據微陀螺加工生產過程中可能產生的微梁梁寬誤差，將驅動微梁梁寬加工誤差分3種情況討論：1)同一對角線上的微梁尺寸相同，即(b1=b4)≠(b2=b3)；2)同一側微梁尺寸相同,即(b1=b2)≠(b3=b4=b)或(b1=b2)≠(b3=b4)；3)只有一根微梁存在加工誤差,即b1≠(b2=b3=b4=b)。

2.1 同一對角線上微梁尺寸相同

2.1.1 對固有頻率和模態的影響

設b1=b4=b+Δ，b2=b3=b-Δ，取加工誤差Δ=0.01，0.02，0.03，0.04，0.05，0.06，0.07，0.08，0.09，0.10 μm。通過有限元分析得到這10種梁寬誤差對微陀螺固有頻率的影響，如圖3所示。

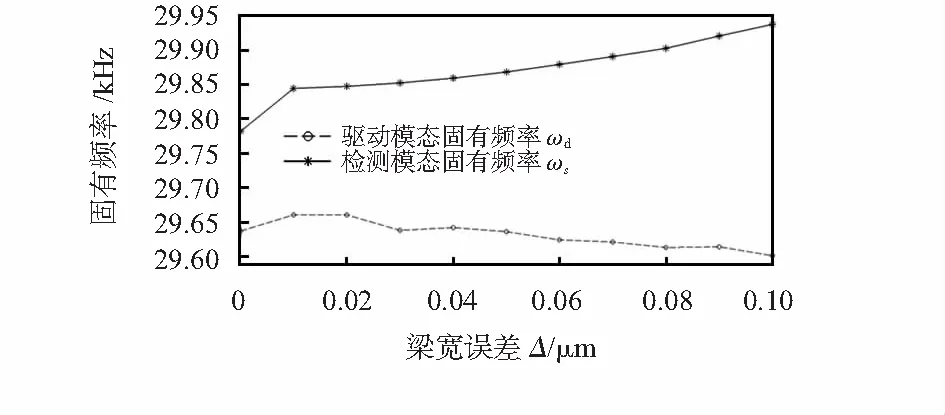
圖3 驅動和檢測模態的固有頻率隨梁寬誤差的變化

由圖3知，微陀螺的驅動模態頻率隨梁寬誤差增大而減小，檢測模態頻率隨梁寬誤差增大而增大，基本上呈線性關系。當梁寬誤差為0.1 μm時，微陀螺的驅動模態頻率減少了0.121 %，檢測模態頻率增加了0.520 %。顯然驅動微梁的加工誤差不僅會影響驅動模態的固有頻率，同時還影響到檢測模態的固有頻率。

由圖4知，驅動模態時其檢測質量塊沿檢測y方向也發生了位移，檢測模態時驅動質量塊沿驅動x方向也發生了位移，即產生模態耦合。理想加工的微陀螺驅動模態時檢測質量塊沿檢測方向的位移為零，檢測模態下驅動方向無位移。顯然這類加工誤差引發了嚴重的模態耦合現象。

圖4 梁寬誤差Δ為0.1 μm時微陀螺模態

對上述10種加工誤差下的模態進行分析，分別量取驅動模態下編號20(如圖2所示)的節點在檢測方向的位移y與驅動方向的位移x，并求其比值得到驅動模態下檢測位移與驅動位移比值隨梁寬誤差的變化規律如圖5所示，根據模態的定義可知，該比值可以用來反映模態耦合的程度。無加工誤差時驅動模態下檢測方向的位移y為0，即y/x值為0；但隨著梁寬誤差不斷增大，y/x值基本上呈線性增長，驅動模態在驅動和檢測兩個方向的耦合程度愈來愈大。當梁寬誤差Δ為0.1 μm時，y/x值達到了0.88。因此這類梁寬誤差會引起驅動模態下檢測質量沿檢測方各的位移，且耦合程度隨誤差的增加而增大。

圖5 梁寬誤差對模態耦合的影響

2.1.2 對微陀螺輸出的影響

微陀螺工作時，在兩端的驅動電極施加帶有直流偏置的交流電壓，梳齒間產生交變的靜電力，該靜電力在其本質上類似于簡諧激振力，因此本文采用有限元仿真實驗研究對微陀螺沿驅動方向施加簡諧激勵模擬交流電壓作用下微陀螺的響應，研究同一對角線微梁相等類型的加工誤差對微陀螺輸出結果的影響。

根據前面分析所得的驅動模態的固有頻率選定諧響應分析的頻率范圍，使驅動方向的固有頻率在該激勵頻率范圍的中間位置，給定20個步數，在動梳齒左端面施加簡諧激振力，直流偏置電壓Vdc=10 V，交流電壓Vac=4 V，根據公式，求出靜電力的幅值為F=6.372×10-8N，微陀螺整體的空氣阻尼系數為C=1.362×10-6kg/s，進行諧響應分析。圖6為梁寬誤差為0.08 μm時節點20在驅動、檢測方向的幅頻曲線。顯然共振峰與驅動頻率對應，此時節點20在驅動方向位移x為5.163×10-5m，在檢測方向位移y為4.008×10-5m，y/x為0.776。

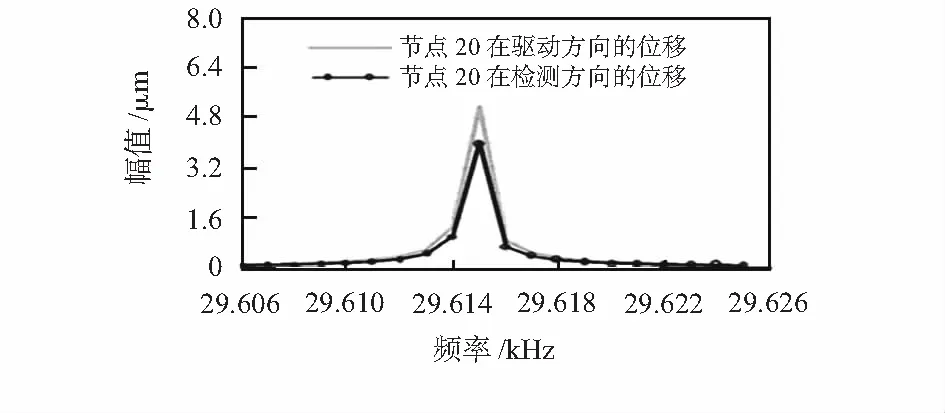
圖6 誤差為0.08 μm時驅動檢測方向的幅頻曲線

同理對其他9種梁寬誤差時的微陀螺進行諧響應分析，提取節點20在激勵頻率等于驅動固有頻率時驅動方向位移x和檢測方向位移y，兩者比值與加工誤差的關系如圖7所示。顯然對角梁尺寸相同類型的加工誤差引起的模態耦合現象會導致微陀螺在無角速度輸入的情況下也存在檢測方向的位移輸出，且該輸出值隨加工誤差的增加而不斷增大，其值之大不可忽略，該種誤差將對微陀螺的正常檢測信號產生嚴重干擾。根據多自由度系統線性振動理論可知，當激勵頻率等于系統的某階固有頻率時，系統將按該階模態振動，圖7中的驅動模態下檢測與驅動方向的位移比與諧振分析結果恰好吻合，與振動理論相吻合，因此，模態耦合會導致微陀螺在檢測信號中產生較高的誤差信號，對微陀螺的檢測信號產生嚴重干擾。

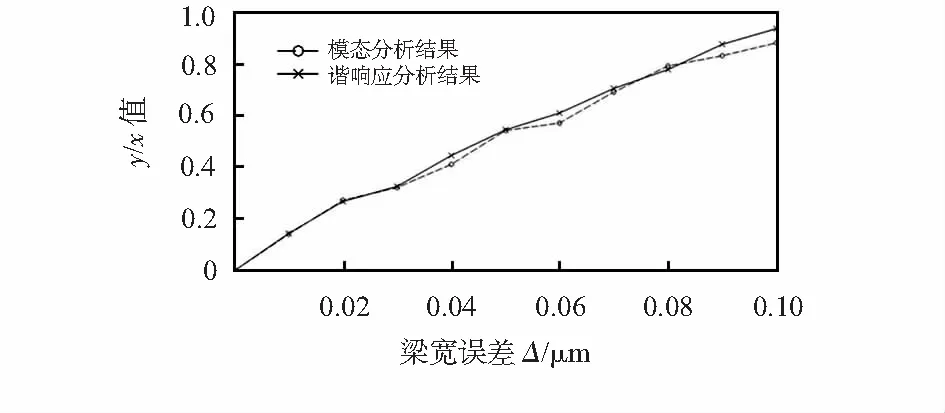
圖7 y/x比值隨梁寬誤差的變化規律

2.2 同側微梁尺寸相同和只一根微梁存在加工誤差

理想微梁梁寬b=2 μm，微梁梁寬的最大加工誤差取Δ=0.10 μm。同側微梁尺寸相同，設：1)b1=b2=b-Δ,b3=b4=b；2)b1=b2=b+Δ,b3=b4=b；3)b1=b2=b-Δ,b3=b4=b+Δ。建立這3種加工誤差下微陀螺的有限元分析模型，對其進行模態分析。只一根存在加工誤差時，設4)b1=b-Δ,b2=b3=b4=b；5)b1=b+Δ,b2=b3=b4=b。分別以第(2)和第(4)為例，結果如圖8所示。

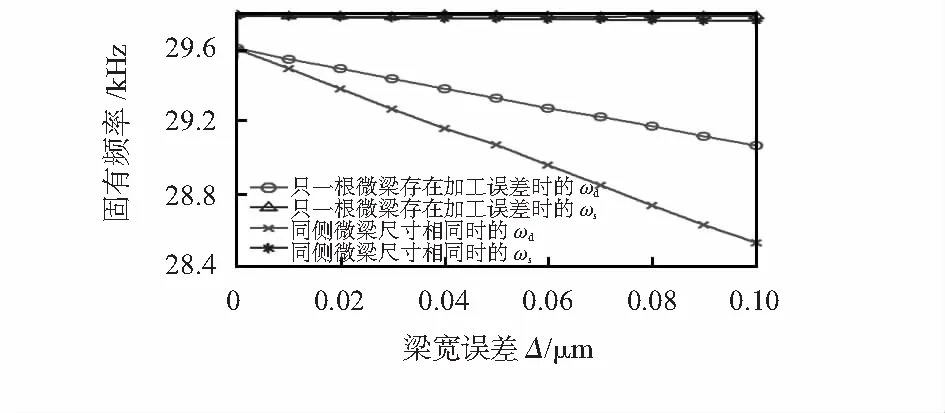
圖8 2種加工誤差對固有頻率的影響

由圖8可得驅動模態的固有頻率都隨著兩類加工誤差的增大而減小，當梁寬誤差為0.1 μm時，驅動模態頻率分別減少3.64 %和1.82，檢測模態頻率的變化可忽略不計。當微梁加工誤差為第(1)和第(3)種時，微陀螺模態與微梁理想加工時基本一致。

如圖9所示，當加工誤差為第(2)種時，第二階為檢測模態，第三階為驅動模態，這種微梁加工誤差導致微陀螺驅動模態、檢測模態順序發生顛倒。只一根微梁存在加工誤差的第(5)種情況同樣引起微陀螺模態階數的顛倒。

圖9 第(2)類誤差下微陀螺模態

從圖9可知，在最大梁寬誤差時，同側微梁尺寸相同時，第(1)種誤差下節點20在驅動模態下的檢測方向位移y與驅動方向位移x的比值為0.016，而諧響應分析的比值為0.018；同理得只一根微梁存在加工誤差時，第(2)種情況下節點20的y/x僅為0.080，諧響應分析結果為0.093，可見這兩類加工誤差的模態耦合現象可以忽略，同時也不會對檢測信號造成嚴重干擾。

3 結 論

1)三類微梁梁寬誤差導致的不等彈性都會不同程度的改變驅動和檢測模態的固有頻率；

2)同側微梁尺寸相同或只一根微梁尺寸存在加工誤差時模態耦合現象可忽略，但會導致驅動模態與檢測模態的階次發生改變；

3)兩對角線上微梁尺寸相同引起的模態耦合現象，在設計中不可忽略，且耦合程度隨加工誤差的增大而增加，當最大梁寬誤差為0.1 μm時模態耦合導致驅動模態下檢測與驅動方向的位移比高達0.88，這類加工誤差會引起嚴重的模態耦合并對檢測信號產生嚴重干擾，應避免這類加工誤差產生。