改進細菌覓食算法在PID參數整定中的應用*

李曉含, 王聯國

(1.甘肅農業大學 機電工程學院,甘肅 蘭州 730070；2.甘肅農業大學 信息科學技術學院,甘肅 蘭州 730070)

0 引 言

細菌覓食優化(bacterial foraging optimization,BFO)算法具有魯棒性強、易于實現、可并行處理與全局搜索的特點[1],在許多領域已廣泛應用,但其存在著收斂速度慢,極易陷入局部最優缺點。文獻[2]將粒子群優化(particle swarm optimization,PSO)與SA結合作為一個PSO-SA變異因子,改善細菌的交流能力；文獻[3,4]將BFO與PSO結合,提高算法的尋優機制；文獻[5]將遺傳算法(genetic algorithm,GA)與BFO算法混合,增大其搜索能力,提出了電力系統無功優化的遺傳—細菌覓食優化混合算法(GA-BFO),文獻[6]在細菌覓食算法趨向操作中,引入碰壁策略優化初始位置,提高收斂速度；文獻[7]提出了定義進化域的方法確定細菌前進方向,解決離散域問題存在的缺陷；文獻[8]提出了自適應步長與概率,解決陷入局部最優問題,并應用于圖像分割中；文獻[9]將粒子群與細菌覓食算法結合,提高了搜索能力,應用于三電平逆變器中；文獻[10]將改進細菌覓食算法應用于軟測量建模中。

本文對細菌覓食算法的趨化操作與遷移操作改進,以加快細菌覓食的搜索速度與尋優精度,并采用測試函數及比例—積分—微分(proportion integration differentiation,PID)參數整定的仿真試驗檢驗效果及可行性。

1 基本細菌覓食算法不足

標準細菌覓食算法包括：趨化、群聚、復制和遷徙，算法存在的問題為：個體間交流信息較少，影響收斂速度。

2 改進的細菌覓食算法

2.1 趨化改進

將粒子群優化算法運用于細菌覓食算法趨化操作中,加大個體間的信息交流,提高收斂速度與精度,則細菌覓食算法在趨化操作時任意方向翻轉移動更新公式為[11]

ψ(j+1)=w×ψ(j)+c1r1(pbest-pcurrent)+

c2r2(gbest-pcurrent)

(1)

權重w在粒子群算法用來平衡算法的全局尋優與局部尋優,當取值大時利于全局尋優,但難以得到精確值；當取值小時利于局部尋優,但易陷入局部極值點。故采用自適應調節方法,即每個粒子依據自身當前適應值來調節變化,即

(2)

式中wmin,wmax[12]分別為最大值與最小值；fi為當前粒子適應值；fav,fmin分別為平均值與最小值。

2.2 遷徙改進

采用自身適應度來調節遷移方式,在遷徙操作時,先對個體適應度值比較,得出最優2個個體不進行遷徙,最差的3個個體直接遷徙,中間則延續一般方式,根據適應度進行動態調整按照式(3)對遷徙概率優化

(3)

式中Pmin與Pmax為遷徙概率最大值與最小值；Jmax與Ji為最好健康適應度值與當前i健康適應度值。

當進化較快時,以低概率進行遷徙,可以保持當前有利信息；當較慢時,易陷入局部最優,需要較高概率遷徙,以跳出局部最優。

2.3 算法主要流程

1)初始化各參數,s,p,Nc,Ned,Nre,Sr,Ped,c1,c2,r1,r2等,其中,s為細菌總個數,p為搜索空間維度,Nc為趨向操作次數,Ned為遷徙操作數,Nre為復制操作數,Sr為細菌總數1/2,Ped為遷徙概率,c1,c2,r1,r2為PSO隨機參數。

2)計算細菌適應度值,將細菌目前適應度值作為個體細菌歷史最好位置,所有細菌適應度最好值作為全局最優。

3)利用新公式更新細菌方向與位置。

4)在返回步驟(2)重新計算適應度值,與歷史最好位置比較,如果更優,將取代歷史最好值。再將結果與群體最優比較,若更優,將其作為全局最優。

5)復制循環,計算適應度值,滿足條件個體復制新個體取代另一半不滿足條件個體。

6)遷徙循環,復制完后生成一個隨機概率,與動態遷徙概率比較,若小于概率,進行遷徙。

7)輸出結果。

3 測試函數

3.1 仿真設計

本文采用6個常見的標準非線性測試函數對細菌覓食算法及改進細菌覓食算法進行測試對比,測試函數最優值一般都難獲得,且隨著維度增加,優化難度隨之急劇加大,測試函數如下：

1)Sphere函數(x∈[-5.12,5.12],最優解為0)

(4)

2)Quartic函數(x∈[-1.28,1.28],最優解為0)

(5)

3)Griewank函數(x∈[-600,600],最優解為0)

(6)

4)Schewefel函數(x∈[-500,500]最優解-12 569.5)

(7)

5)Rastrigrin函數(x∈[-5.12,5.12],最優解為0)

(8)

6)Ackley函數(x∈[-32,32],最優解為0)

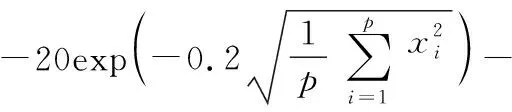
3.2 仿真結果與分析

本文細菌覓食算法參數選取值參考文獻[13],設置測試函數維度為30；細菌種群規模為30；Nc為40；游動次數為5次；復制次數為5次；遷徙次數為5次,仿真結果表1。

表1 固定迭代次數下尋優結果(四舍五入值)

表1為原始與改進細菌覓食算法在測試每個函數時,獨立運行20次結果。由平均值可以看出：較難獲得全局最優解的Rastrigrin函數與函數Ackley函數提高了尋優精度,獲得較優的值；Griewank函數尋優精度提高約有5個數量級；其他測試函數也獲得較好的尋優解；說明改進細菌覓食算法對易陷入局部最優特點得到改善。從運行時間列可以看到,改進細菌覓食算法運行時間較短,說明改進后的搜索速度要快些。因此,改進細菌覓食算法在尋優進度和搜索速度上均得到一定改善,驗證了算法的可行性與有效性。

4 應用實例

為了達到更好的控制效果,本文在PID控制器參數優化設計中,采用細菌覓食優化算法優化調整PID的ki,kp,kd3個參數,實現輸入與輸出的實時跟蹤。細菌覓食智能算法PID控制結構如圖1所示。

圖1 智能控制

圖1中,r(t)為系統輸入函數；y(t)為系輸出函數；U(t)為控制器輸出。

4.1 被控對性

本文采用一階系統與一階慣性延遲兩個基本模型,進行PID控制仿真實驗,其被控對性為

(9)

4.2 目標函數

評價誤差性能選用時間誤差絕對積分(integral of time multiplied absolute value of error,ITAE)作為目標函數,其公式為

(10)

4.3 編 碼

在整定中,PID控制器參數設置為細菌在空間中位置,在細菌覓食算法中,v表示算法的維度,則用一組參數向量Xi=(x1,x2,…,xv)表示細菌所在的位置,ki,kp,kd為細菌覓食算法中的優化參數,細菌覓食算法的位置則定義為 (ki,kp,kd)。在參數整定中,將個體值依次賦給參數ki,kp,kd,然后到運行控制系統Simulink模型,得到對應的性能指標,該指標傳遞到細菌覓食算法中作為適應度值,進行一步對比優化,最后退出算法[14]。PID參數整定流程如圖2。

4.4 仿真結果與分析

采用MATLAB軟件進行仿真,對PID參數整定,用改進細菌覓食進行擇優,并將改進結果與原始算法在性能指標對比。

圖2 參數整定運行

表2所示為控制性能指標,性能指標ITAE取值越小,其超調量越小,則系統的穩定性越好;反之,系統穩定性較差。在性能評價指標ITAE中,改進細菌覓食算法中ITAE獲得值更小,則改進細菌覓食算法整定參數用于系統獲得更穩定的效果。

表2 控制性能指標

圖3為原始BFO算法與改進BFO算法得到參數代入系統中所得到的相應系統階躍響應曲線。上升時間為第一次達到穩定時間,從圖3可知：改進后BFO算法與原始BFO算法相比,其上升時間較快；而峰值時間與調整時間的速度均用了評價系統的響應速度,從圖3可知到達峰值時間與調整時間都較快,具有更快的反應速度。

圖3 對象階躍響應曲線

圖4為BFO算法和改進BFO算法優化的ITAE變化曲線。從圖4中可以看出,改進BFO算法在迭代120次左右收斂,原始細菌覓食算法在280次左右得到收斂,得出改進算法收斂速度更好些,可以得出改進算法有效性及適用性。

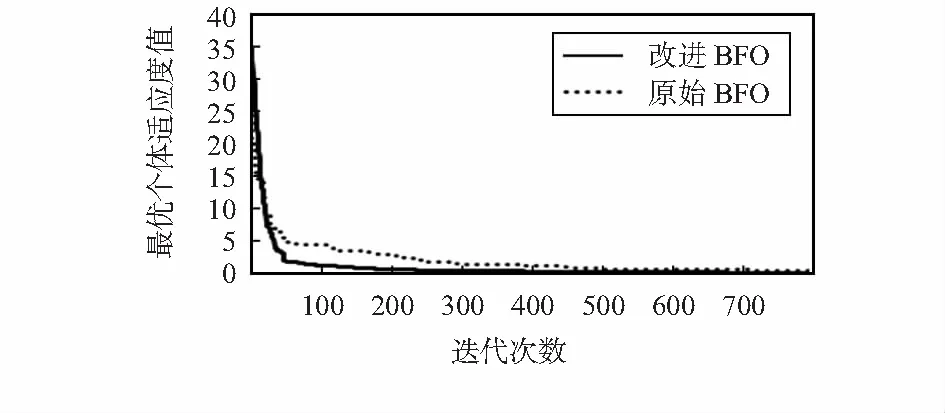
圖4 2算法的迭代曲線

可知,改進細菌覓食算法在PID整定應用中,其階躍響應的超調量減少,收斂速度與反應時間得到提升,系統響應速度快,控制品質得到了很大改善。

5 結 論

針對細菌覓食算法存在收斂速度不夠快,易陷入局部極值等不足,提出了一種細菌覓食改進算法,對趨化操作與遷徙操作進行改進。用標準測試函數和PID參數整定實驗,對改進細菌覓食算法進行測試,結果表明該改進方法可以提高尋優精度與搜索速度。