適合多密度的DBSCAN改進(jìn)算法*

侯思祖, 韓思雨, 韓利釗, 錢(qián)雪忠

(1.華北電力大學(xué) 電子與通信工程系,河北 保定 071003；2 江南大學(xué) 物聯(lián)網(wǎng)技術(shù)應(yīng)用教育部工程研究中心,江蘇 無(wú)錫 214122)

0 引 言

作為數(shù)據(jù)挖掘的重要手段之一,聚類(lèi)分析已經(jīng)應(yīng)用到很多領(lǐng)域。如文獻(xiàn)[1]提出了基于聚類(lèi)分析的SAR圖像變化檢測(cè),應(yīng)用到圖像處理中；文獻(xiàn)[2]將模糊C均值聚類(lèi)方法應(yīng)用于火災(zāi)預(yù)警。具有噪聲的基于密度的空間聚類(lèi)(density-based spatial clustering of application with noise,DBSCAN)[3]算法,存在2方面問(wèn)題：1)DBSCAN算法需要用戶在無(wú)先驗(yàn)知識(shí)的情況下輸入2個(gè)參數(shù)Eps和MinPts,對(duì)聚類(lèi)結(jié)果影響很大,特別是在密度分布不均勻的多密度數(shù)據(jù)中,聚類(lèi)效果不理想。2)DBSCAN時(shí)間復(fù)雜度為O(N2),限制了其處理大規(guī)模數(shù)據(jù)的能力。一些研究人員提出了將傳統(tǒng)網(wǎng)格劃分算法[4～6]的思想用于DBSCAN算法中。

本文提出了一種適合多密度的DBSCAN聚類(lèi)算法,實(shí)驗(yàn)驗(yàn)證了算法能有效地實(shí)現(xiàn)多密度、任意形狀的數(shù)據(jù)分類(lèi)。

1 DBSCAN算法

1.1 DBSCAN算法的相關(guān)理論

DBSCAN算法的基本思想是：計(jì)算每個(gè)數(shù)據(jù)對(duì)象以Eps為半徑的鄰域內(nèi)數(shù)據(jù)的個(gè)數(shù),如果達(dá)到密度閾值MinPts，歸為一類(lèi),用密度可達(dá)將高密度區(qū)域連通形成簇。給定一個(gè)包含n個(gè)數(shù)據(jù)的d維數(shù)據(jù)集D,給定Eps和MinPts,DBSCAN算法中的相關(guān)定義如下：

定義1 數(shù)據(jù)對(duì)象?p∈D的Eps鄰域NEps(p)定義為以p為核心,Eps為半徑的d維超球體區(qū)域內(nèi)包含的點(diǎn)的集合,即NEps(p)={q∈D|dist(p,q)≤Eps},dist(p,q)為D中數(shù)據(jù)p和q之間的距離。

定義2 對(duì)于數(shù)據(jù)對(duì)象p,如果p的Eps鄰域內(nèi)包含的對(duì)象個(gè)數(shù)滿足|NEps(p)|≥MinPts,稱(chēng)p為核心對(duì)象。

定義3 對(duì)于數(shù)據(jù)對(duì)象p,q∈D,滿足q∈NEps(p)且|NEps(p)|≥MinPts,稱(chēng)q從p關(guān)于Eps,MinPts直接密度可達(dá)。直接密度可達(dá)不滿足對(duì)稱(chēng)性,如圖1(a)所示。

定義4 對(duì)于數(shù)據(jù)對(duì)象q,p∈D,如果存在對(duì)象序列p1,p2,…,pn∈D,其中,p1=q,pn=p,且pi+1為從pi直接密度可達(dá),則稱(chēng)p為從q關(guān)于Eps,MinPts。密度可達(dá)如圖1(b)所示,p3為從p1關(guān)于Eps,MinPts密度可達(dá)。密度可達(dá)不滿足對(duì)稱(chēng)性。

定義5 對(duì)于數(shù)據(jù)對(duì)象q,p∈D,如果存在一個(gè)數(shù)據(jù)o使得p和q均從o密度可達(dá),則稱(chēng)p和q關(guān)于Eps,MinPts密度相連。因此,密度相連滿足對(duì)稱(chēng)性。如圖1(c)所示。

圖1 DBSCAN相關(guān)概念

1.2 DBSCAN算法步驟

當(dāng)給定Eps和MinPts時(shí),DBSCAN算法的核心思想為尋找密度相連的最大集合。具體步驟如下：

輸入：數(shù)據(jù)集D,參數(shù)Eps和MinPts。

輸出：帶有類(lèi)標(biāo)簽的聚類(lèi)結(jié)果。

1)從數(shù)據(jù)集D中隨機(jī)取出一個(gè)未處理的數(shù)據(jù)p,掃描數(shù)據(jù)集D,查看p的鄰域數(shù)據(jù)的個(gè)數(shù)。

2)如果|NEps(p)|≥MinPts,查找密度相連所有數(shù)據(jù),作類(lèi)標(biāo)簽并標(biāo)記已處理；否則，標(biāo)記已處理過(guò),不標(biāo)記類(lèi)標(biāo)簽,下次取數(shù)據(jù)時(shí)不再考慮,等待其他數(shù)據(jù)進(jìn)行密度可達(dá)或者密度相連時(shí)處理。

3)重復(fù)步驟(1)、步驟(2),直到所有數(shù)據(jù)均標(biāo)記已處理,對(duì)于未類(lèi)標(biāo)記的數(shù)據(jù)作為噪聲處理,聚類(lèi)結(jié)束。

可以看出數(shù)據(jù)共分為3種：在其鄰域內(nèi)的數(shù)據(jù)達(dá)到密度閾值MinPts；邊界點(diǎn),其鄰域內(nèi)的數(shù)據(jù)未達(dá)到密度閾值,但為某一個(gè)核心對(duì)象的直接密度可達(dá)點(diǎn)；噪聲點(diǎn),其鄰域內(nèi)數(shù)據(jù)達(dá)不到密度閾值,且不在任何一個(gè)核心對(duì)象的鄰域內(nèi)。

2 適合多密度的DBSCAN改進(jìn)算法

首先根據(jù)核心點(diǎn)鄰域內(nèi)密度的大小對(duì)數(shù)據(jù)集進(jìn)行排序,然后自適應(yīng)的選取適合本鄰域的密度閾值MinPts進(jìn)行聚類(lèi)。一方面能夠使DBSCAN算法處理多密度數(shù)據(jù)；另一方面,可以避免數(shù)據(jù)的輸入順序?qū)垲?lèi)結(jié)果的影響。

2.1 數(shù)據(jù)預(yù)處理

輸入數(shù)據(jù)集D,給定半徑參數(shù)Eps,掃描數(shù)據(jù)集依次計(jì)算每個(gè)數(shù)據(jù)對(duì)象與其他數(shù)據(jù)對(duì)象的距離并以此給數(shù)據(jù)集D加屬性A,A所記錄的內(nèi)容為：當(dāng)前數(shù)據(jù)對(duì)象在半徑Eps鄰域內(nèi)的對(duì)象個(gè)數(shù)。以屬性A為標(biāo)準(zhǔn),對(duì)數(shù)據(jù)集D降序排序。排序后數(shù)據(jù)集設(shè)為D1,作為DBSCAN算法的輸入,數(shù)據(jù)對(duì)象輸入順序基本上代表了該對(duì)象所在簇密度的高低。

2.2 自適應(yīng)獲取密度閾值

定義6 初始核心對(duì)象：每一個(gè)簇聚類(lèi)開(kāi)始時(shí)第一個(gè)核心對(duì)象。

首先根據(jù)高密度簇(即數(shù)據(jù)集D1的第一個(gè)數(shù)據(jù)所在的簇)獲取一個(gè)初始的密度閾值MinPts,該參數(shù)僅用于對(duì)第一個(gè)簇進(jìn)行聚類(lèi),聚類(lèi)結(jié)束后,從未被聚類(lèi)的數(shù)據(jù)對(duì)象中選取屬性A最大的對(duì)象作為核心對(duì)象,自適應(yīng)地獲取密度閾值MinPts

(1)

式中NEps(A)為當(dāng)前數(shù)據(jù)對(duì)屬性A的值；NEps(maxA)為數(shù)據(jù)集D1第一個(gè)數(shù)據(jù)對(duì)象屬性A的值。每聚類(lèi)一次,密度閾值隨著初始核心對(duì)象鄰域的密度值改變。

根據(jù)不同密度使用不同的密度閾值,使DBSCAN算法對(duì)數(shù)據(jù)分布的適應(yīng)性更強(qiáng)。

2.3 算法具體描述

對(duì)數(shù)據(jù)集進(jìn)行預(yù)處理,根據(jù)輸入的參數(shù)Eps和MinPts以第一個(gè)數(shù)據(jù)對(duì)象作為初始核心對(duì)象,進(jìn)行聚類(lèi)；在未被處理的數(shù)據(jù)中選取屬性A的值最大的對(duì)象作為初始核心對(duì)象；依次進(jìn)行下去,直到剩余未處理的數(shù)據(jù)無(wú)法形成一個(gè)類(lèi)為止(剩余任何對(duì)象中在其Eps鄰域范圍內(nèi)的數(shù)據(jù)個(gè)數(shù)小于4)。

當(dāng)給定Eps和MinPts時(shí),適合多密度的DBSCAN算法的具體步驟如下：

輸入：數(shù)據(jù)集D,參數(shù)Eps和MinPts。

輸出：帶有類(lèi)標(biāo)簽的聚類(lèi)結(jié)果。

1)根據(jù)參數(shù)Eps對(duì)數(shù)據(jù)進(jìn)行預(yù)處理,生成含有屬性A的數(shù)據(jù)集D1；

2)選取D1中第一個(gè)數(shù)據(jù)作為初始核心對(duì)象,用參數(shù)Eps和MinPts進(jìn)行DBSCAN擴(kuò)展聚類(lèi),并對(duì)已經(jīng)聚類(lèi)的數(shù)據(jù)做已處理標(biāo)記,直到該簇聚類(lèi)結(jié)束；

3)從未被聚類(lèi)的數(shù)據(jù)中按D1的順序選取初始聚類(lèi)核心對(duì)象,利用獲得的密度閾值和半徑參數(shù)Eps進(jìn)行DBSCAN擴(kuò)展聚類(lèi)；

4)重復(fù)步聚(3),剩余的對(duì)象不存在核心對(duì)象時(shí),聚類(lèi)結(jié)束。

2.4 時(shí)間復(fù)雜度分析

設(shè)聚類(lèi)結(jié)果最終生成K個(gè)簇K?N,N為數(shù)據(jù)對(duì)象個(gè)數(shù),相較于DBSCAN算法,該算法在時(shí)間上只多了2部分：數(shù)據(jù)預(yù)處理的時(shí)間,時(shí)間復(fù)雜度為O(n2)；計(jì)算密度閾值時(shí)間,在聚類(lèi)過(guò)程中共計(jì)算K-1次,時(shí)間可以忽略不計(jì)。綜上,本文提出的算法時(shí)間復(fù)雜度依然為O(N2)。

3 實(shí)驗(yàn)結(jié)果與分析

本文所提算法通過(guò)MATLAB工具實(shí)現(xiàn)并處理實(shí)驗(yàn)結(jié)果。實(shí)驗(yàn)環(huán)境是：CPU為Intel i3 3.7 GHz；內(nèi)存為4 GB；OS為Windows7。對(duì)比了經(jīng)典的DBSCAN算法和文獻(xiàn)[7]提出的針對(duì)多密度的DBSCAN改進(jìn)算法。

實(shí)驗(yàn)所有結(jié)果中的“×”為噪聲點(diǎn)；相同顏色和形狀的為一個(gè)簇；設(shè)MP為密度閾值。

實(shí)驗(yàn)1 數(shù)據(jù)集DS1共含有1 927個(gè)數(shù)據(jù),4個(gè)密度不相同的簇,且含有臨界點(diǎn)干擾。聚類(lèi)結(jié)果如圖2所示。

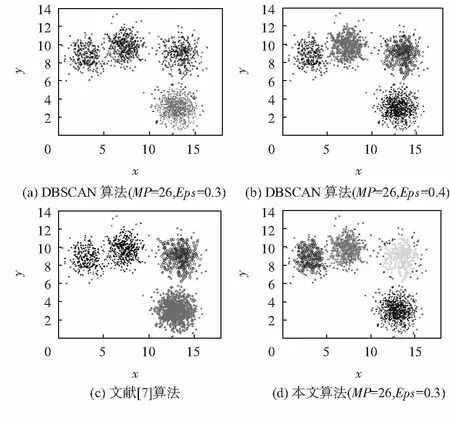
圖2 DS1聚類(lèi)結(jié)果

圖2(a)、圖2(b)本文算法中右下角的簇密度最大,左上角的簇密度較小,且相距較近。圖2(a)中僅有高密度區(qū)域可以形成簇,低密度區(qū)域當(dāng)作噪聲；圖2(b)中增加聚類(lèi)半徑,但仍未識(shí)別出密度較小的簇,如果再繼續(xù)增加聚類(lèi)半徑，左上角2個(gè)簇被合并成一個(gè)簇；圖2(c)中自適應(yīng)地找到適合本密度的聚類(lèi)半徑,但左上角2個(gè)簇相聚較近,被合并成了一個(gè)簇；圖2(d)中每個(gè)簇會(huì)根據(jù)初始聚類(lèi)核心對(duì)象鄰域內(nèi)數(shù)據(jù)個(gè)數(shù)自適應(yīng)的生成密度閾值,準(zhǔn)確識(shí)別出了4個(gè)簇。

實(shí)驗(yàn)2 數(shù)據(jù)集DS2共8 000個(gè)數(shù)據(jù),8個(gè)簇,包括多個(gè)不同的密度和不同形狀，實(shí)驗(yàn)結(jié)果如圖3所示。

實(shí)驗(yàn)2中的聚類(lèi)結(jié)果與實(shí)驗(yàn)1結(jié)果類(lèi)似,由圖3(a)、圖3(b)可以看出，在保證相鄰高密度簇不被合并的情況下,就要損失低密度區(qū)域。圖3(c)與實(shí)驗(yàn)1情況相同。圖3(d)準(zhǔn)確識(shí)別出了8個(gè)簇。

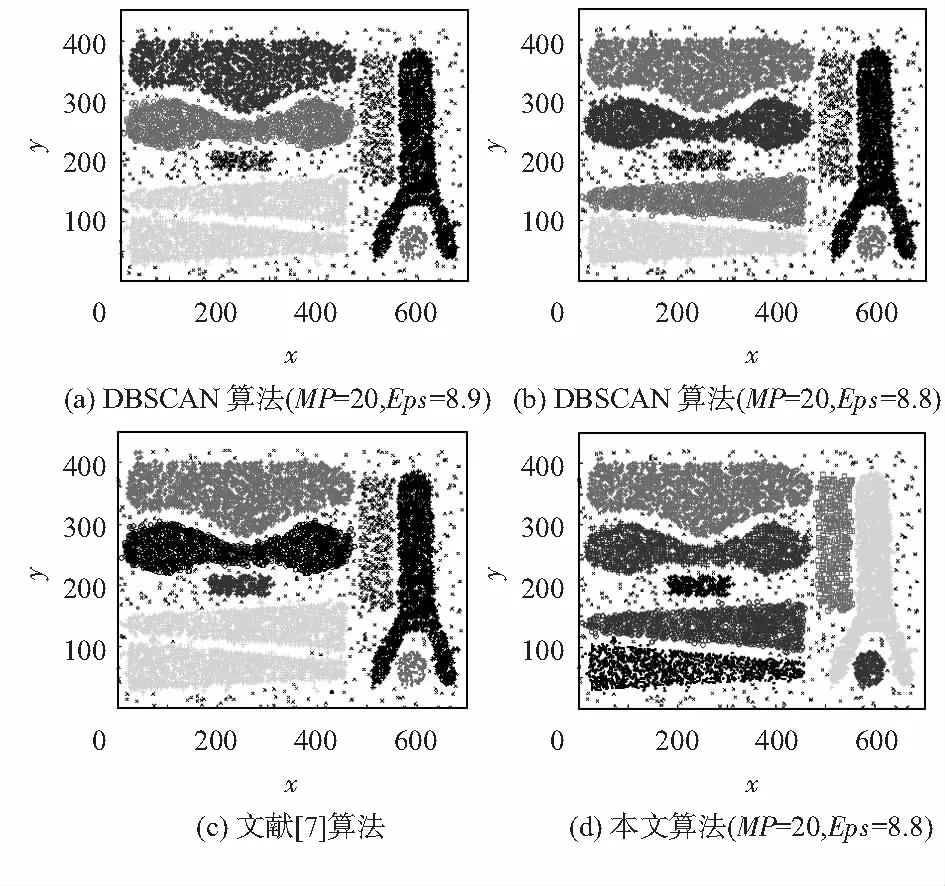
圖3 DS2聚類(lèi)結(jié)果

實(shí)驗(yàn)3 數(shù)據(jù)集DS3來(lái)源于文獻(xiàn)[9]的真實(shí)數(shù)據(jù)集Chameleon,共8 000個(gè)數(shù)據(jù),6個(gè)類(lèi)簇,實(shí)驗(yàn)對(duì)比了經(jīng)典的DBSCAN算法與2016年馮振華等人提出的針對(duì)多密度聚類(lèi)的DBSCAN改進(jìn)算法,實(shí)驗(yàn)結(jié)果如圖4所示。

圖4 DS3聚類(lèi)結(jié)果

圖4(a)中僅識(shí)別出4個(gè)簇,造成大量簇信息丟失；圖4(b)中試圖增加半徑參數(shù),識(shí)別圖4(a)中未識(shí)別的簇,效果較好,識(shí)別出5個(gè)簇。圖4(c)中識(shí)別出了6個(gè)簇,且簇與簇之間的連接處的“橫線”干擾數(shù)據(jù)進(jìn)行了準(zhǔn)確識(shí)別,但邊界處吸收量較多的噪聲。圖4(d)識(shí)別出了6個(gè)簇,且邊界數(shù)據(jù)處理較好,中間“橫線”的識(shí)別稍有瑕疵。

4 結(jié)束語(yǔ)

經(jīng)過(guò)理論分析和實(shí)驗(yàn)證明,本文提出的適合多密度的DBSCAN聚類(lèi)算法,可以在一定程度上弱化參數(shù)對(duì)聚類(lèi)結(jié)果的影響,對(duì)數(shù)據(jù)分布的適應(yīng)能力更強(qiáng),聚類(lèi)效果更優(yōu)。但在效率上與原算法大致相同,不太適合大規(guī)模數(shù)據(jù)的聚類(lèi)。