大洋富鈷結殼的超聲測厚

，，

(1.青島科技大學 自動化與電子工程學院，青島 266100；2.國家深海基地管理中心，青島 266200)

深海富鈷結殼是繼大洋多金屬結核之后發現的另一種重要的礦產資源。富鈷結殼是生長在水深為400～4 000 m的平頂海山、海臺頂部或坡上的殼狀物[1],其中富含鈷、鎳、鋅、鉛、鈰、鉑等金屬，其厚度范圍為2～8 cm[2]，是多金屬結核中鈷含量的4倍。

目前,日本東京大學搭配BOSS-A型ROV(水下機器人)研究了一款測量富鈷結殼厚度的裝置，實現了ROV水下工作時對富鈷結殼的原位探測。國內何清華[3]等對使用聲波檢測富鈷結殼厚度進行過初步探討，但受限于國內載人潛水器技術的發展，一直未能得到實現。筆者針對“蛟龍”載人潛水器水下作業時需對富鈷結殼厚度實時測量的問題，對搭載載人潛水器的測厚系統進行了研究。

1 超聲測厚原理與富鈷結殼特性分析

聲波在傳播過程中，會在傳播介質的聲阻抗發生改變時，即在兩種不同介質的邊緣處產生反射現象。因此，假設已知某種被測物體的聲波速度，只要被測物體與底部介質之間存在不同的聲阻抗，就有可能通過測量從被測物體表面至被測物體底部的渡越時間來計算出該被測物體的厚度，也就是文中采用的測厚方法。

富鈷結殼的生長環境十分復雜，基巖種類在不同的海山區會有不同的類別；同時由于受到長期的腐蝕，即使是同類別的基巖，其聲阻抗也會存在差異。當富鈷結殼與其下伏基巖的聲阻抗相差很小時，聲波的反射波會變得非常微弱以至于無法通過技術手段對其進行檢測，從而導致使用渡越時間無法得到富鈷結殼的厚度信息。

事實上，富鈷結殼的聲阻抗大約為5.64×106kg·m-2·s-1[4]，這意味著富鈷結殼下伏基巖的聲阻抗小于5.64×106kg·m-2·s-1時，聲波將不會在邊緣處發生反射。新鮮的玄武巖、磷灰巖以及某類型的角礫巖等都與富鈷結殼存在較大的聲阻抗對比，因此使得測厚工作成為可能。但即使在上述情況下，實際測量時仍然有許多困難，因此筆者設計出了針對富鈷結殼特點的測厚算法。

目前，海底聲波的檢測中，大多采用低頻聲波信號，通過分析聲波信號來反演地質結構。但如果使用低頻聲波信號，則沒有足夠的分辨率去分析只有幾厘米厚的海底表層。而對于富鈷結殼來說，其表面粗糙度情況將更為復雜。在這種情況下，表面的高能量聲波反射將會掩蓋來自富鈷結殼與下伏基巖交界面處反射的聲波，使其無法解調，因此低頻信號不具有必要的空間與時間分辨率來解決富鈷結殼的厚度測量問題。綜上所述，研究采用2.25 MHz的高頻換能器來解決上述問題。

2 測厚系統設計

采用收發一體的超聲波探頭，測厚系統由兩部分組成，分別為超聲波發射接收部分與ARM(Advanced RISC Machine)處理器部分。

該系統擬采用ARM芯片處理器，主要由最小系統模塊、LCD(液晶顯示器)模塊、鍵盤模塊、RS485通信模塊等組成，其中RS485用于實現下位機與載人潛水器控制系統間的通信，其系統組成如圖1所示。

圖1 測厚系統組成示意

2.1 發射電路設計

上述總體設計中，由ARM芯片發射PWM(脈沖寬度調制)方波信號進入發射電路，通過發射電路中的功率放大功能，產生能夠驅動超聲波探頭的激勵電壓，激勵超聲波換能器發射聲波。ARM芯片發射PWM方波信號，該信號經過三極管放大后，再經過一定匝數比的變壓器升壓，從而獲得足夠的功率以驅動超聲波換能器，變壓器主要用于升高脈沖電壓，并且使輸出阻抗與超聲波換能器的阻抗相匹配。超聲波發射電路設計示意如圖2所示(T1為變壓器元件；PNP為二極管；GND為電線接地端)。

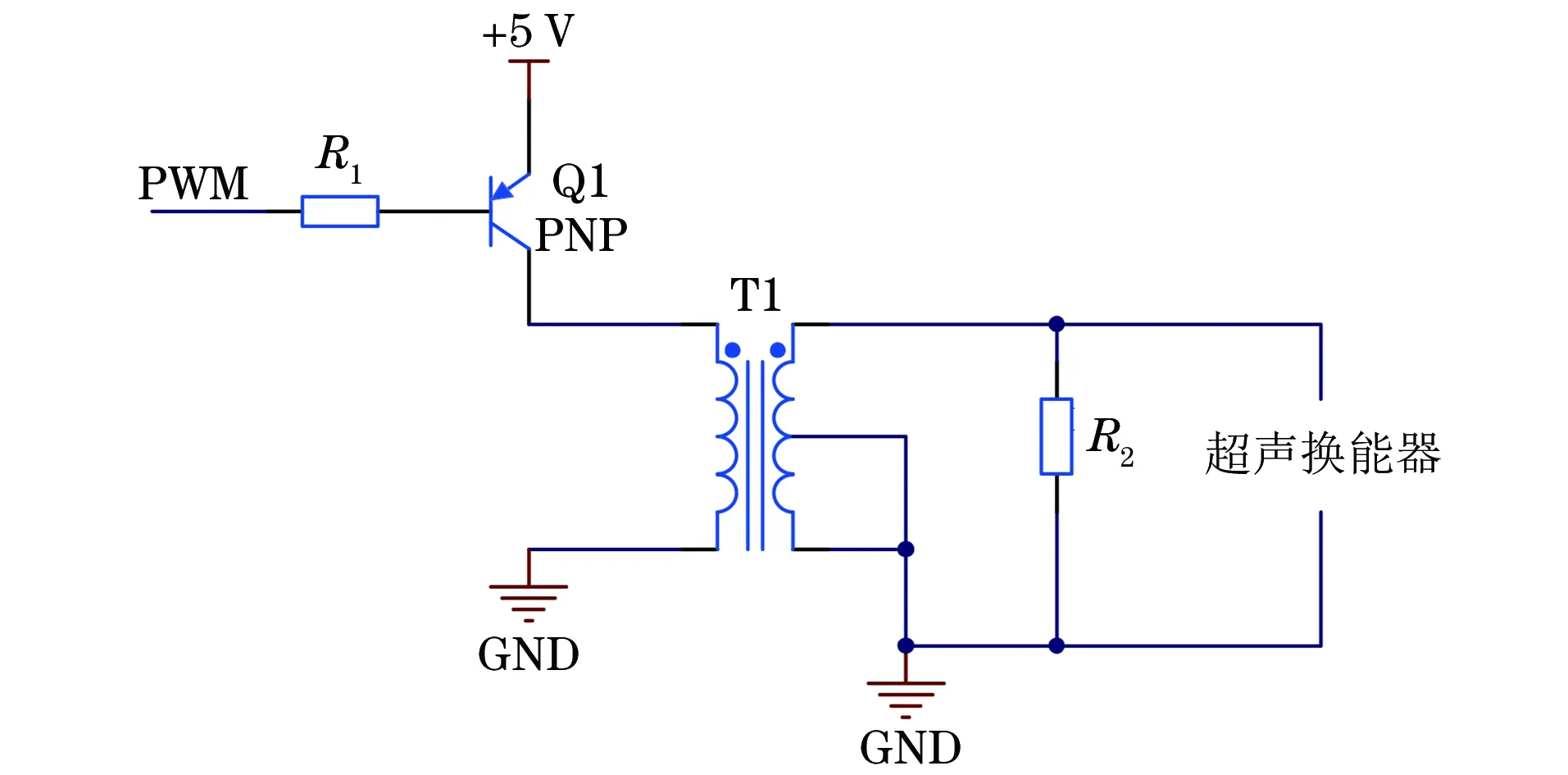
圖2 超聲波發射電路設計示意

2.2 接收電路設計

超聲波接收電路組成示意如圖3所示。由于換能器接收到的原始信號強度太小且不穩定，為了實現高精度測量，必須要對原始信號進行處理。該模塊主要包括信號放大電路、濾波電路、AD(數字模擬)采集電路等部分。

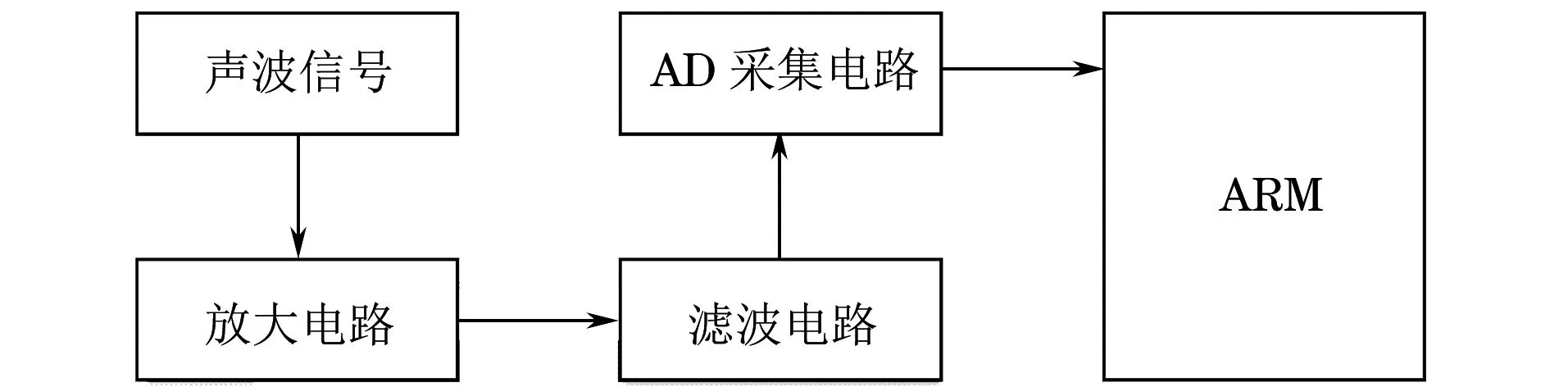
圖3 超聲波接收電路組成示意

當超聲波換能器接收到返回的聲波信號后，先經過放大電路對微弱信號進行放大；同時原始信號中的噪聲信號也必然會被放大，因此需要對信號進行濾波處理，使用電感和電容，并選擇合適的參數組成LC(諧振電路)濾波器對信號進行濾波處理。

將處理好的信號用高速AD芯片進行采集，完成模擬信號到數字信號的轉換。由于探頭的頻率為2.25 MHz，因此采樣頻率需要大于4.5 MHz。

3 檢測算法的設計

由于富鈷結殼內部結構的復雜性，簡單地通過計算第一次接收回波信號的方法并不能夠準確地計算出富鈷結殼的真實厚度。因此，設計了一種峰值檢測算法來自動測量富鈷結殼的厚度。峰值檢測算法框圖如圖4所示(SNR為信噪比)。

圖4 峰值檢測算法框圖

假設已接收到的反射信號為G(t)，G(t)為某次激勵換能器后在固定周期內產生反射回波的一組離散數據點。首先G(t)信號通過帶通濾波器，得到在探頭頻率范圍內的信號Gf(t)，將信號通過Hilbert(希爾伯特)變換得到其包絡信號H[Gf(t)]。

對該Hilbert信號的信噪比進行檢測，以判斷是否能夠作為峰值檢測的信號。

(1)

式中：qS/N是一個小于1的常量。

若滿足式(1)，則信號進入頂部峰值判斷的窗口函數中，窗口函數通過閾值檢測的方法得到峰值，且閾值大小會根據信號的最大幅值進行自適應調整；若不滿足式(1)則返回等待下一時刻的信號。其中被測物頂部與底部的閾值大小分別通過式(2)，(3)來確定。

?top=qtopmaxH[Gf(t)]

(2)

?bot=qbotmaxH[Gf(t)]

(3)

式中：qtop和qbot為值小于1的常量;?top為頂部閾值;?bot為底部閾值。

在確定閾值后利用式(4)，(5)，對頂部峰值位置進行檢測。

maxH[Gf(ti,…,ti+n)]>?top

(4)

H[Gf(ti)]>H[Gf(ti+1)]+δ

(5)

式中：n為檢測窗口函數的寬度；δ為相對于其臨近峰值的最小高度的閾值。

如果滿足式(4)，(5)，滿足條件的峰值將會被標記為被測物頂部表面的反射峰值，其時間被標記為ttop及ti=tbot。若不滿足，檢測窗口將移動半個寬度，即令ti=ti+n/2(i=0，1,…)，并重復驗證式(4)與式(5)。

在確定ttop后，算法下一步將根據式(6)對被測物底部進行檢測。

maxH[Gf(ttop+tmin…+ttop+tmax)]>?bot

(6)

式中：tmin與tmax分別為可測富鈷結殼的最小厚度與最大厚度的渡越時間。

若上述條件滿足，其時間被標記為tbot及tbot=ttop+Δt(tmin≤Δt≤tmax)，就可以通過測量超聲波在富鈷結殼介質內的渡越時間來估算出其厚度。時間間隔為Δt,富鈷結殼的P波速度為cP,可根據式(7)推算出厚度。

(7)

式中：d為富鈷結殼的厚度;cP設定為一個恒定的聲速。

使用該峰值檢測算法能夠對頂部峰值與底部峰值進行有效識別，提高了檢測精度。由于對富鈷結殼測厚的目的是開發一套礦量估算系統，該系統可以對某海區下富鈷結殼進行持續的厚度測量，以便估算該海區的結殼礦量，故需要對大量數據進行檢測處理。而上述峰值檢測算法能夠實時完成大量數據的處理。另外，使用以上檢測算法有利于節約成本。

4 試驗過程

4.1 試驗材料與設備

圖5 測試中使用的富鈷結殼樣品外觀

選擇4塊結構層次明顯的富鈷結殼進行試驗，測試中使用的富鈷結殼樣品外觀如圖5所示，試驗樣品尺寸及結構特征如表1所示，試驗原理示意如圖6所示，試驗裝置外觀如圖7所示。

圖6 試驗原理示意

圖7 試驗裝置外觀

4.2 試驗結果

將設計的檢測算法應用于試驗獲取的數據上，圖8為4塊富鈷結殼樣品的反射波形與包絡分析，圖中標記了通過算法找到的被測物的頂部信號與底部信號，可通過對應的時間間隔計算得到厚度。

表1 試驗樣品尺寸及結構特征

試驗中cP設定為2 750 m/s，通過圖8中的算法處理后得到時間，再計算得到對應的厚度，其測量值與實際厚度如表2所示。

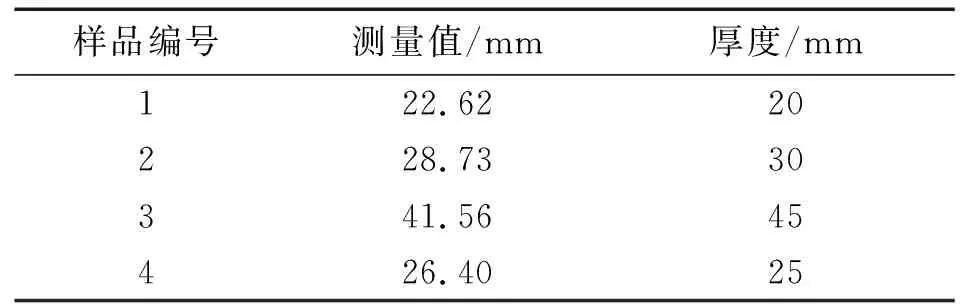
表2 4種樣品的測厚結果

圖8 4塊富鈷結殼樣品的反射波形與包絡分析

根據得到的測量結果可知，測量值與真實值之間存在誤差，分析認為這主要是由于對真實值標定時的測量誤差導致。事實上，在計算過程中考慮到外界壓力等因素的變化還應當對時間進行補償，但試驗中暫不對壓力進行討論。結果表明，利用該檢測算法能夠有效地對厚度進行檢測，且檢測誤差在毫米級，對于海底環境的測量，誤差在可接受范圍內。

5 結語

文章針對載人潛水器的超聲測厚系統進行了研究，分析了富鈷結殼的特性，并對硬件系統進行了設計。設計了一種用于富鈷結殼測厚的峰值檢測算法，并將試驗中從數字示波器得到的數據進行了處理，對厚度檢測結果與真實樣品厚度進行了對比，厚度檢測結果的精度較高。