基于小波包與改進的PSO-PNN變壓器勵磁涌流識別算法研究*

公茂法，接怡冰，李美蓉，解云興，宋健，吳娜

(1．山東科技大學電氣與自動化工程學院，山東青島266590;2．國網山東省電力公司棗莊供電公司，山東棗莊277100;3．國網山東省電力公司東營供電公司東營方大電力設計規劃有限公司，山東東營257091)

0 引言

在以特高壓電網為骨干網架的智能電網建設過程中，電壓等級逐步提高，用戶用電量越來越高，電力系統規模逐漸擴大［1］。變壓器是電力系統中的核心部分，相當于“心臟”，它的運行狀態關乎著整個電力系統的安全。一旦出現故障，將會立即導致整個區域內的電力網癱瘓。因此，對變壓器進行定期的檢查、維修，能夠及時彌補設備缺陷、消除隱患，這對變壓器來說是極為重要的［2］。

在現場實際生產中，電流縱聯差動保護的原理簡單，且具備快速切除各類故障等特點，因而逐漸成為了變壓器首選的主保護之一。將差動保護投入到變壓器中，并不能完全可靠地保護變壓器，有可能產生誤動，導致其誤動的關鍵性因素就是變壓器鐵芯飽和引起的勵磁涌流［3］。

在此背景下，本文提出“基于小波包與改進PSO－PNN網絡的變壓器勵磁涌流識別算法”，此算法能夠可靠區分勵磁涌流和內部故障電流，成功解決導致變壓器差動保護誤動的因素。小波包分析能夠對被測信號進行不同尺度分解以及聚焦到任意細節，很有利于提取特征向量。通過改進PSO算法優化PNN網絡既能夠提高準確度，又能更好地與小波技術相結合，極大提高識別勵磁涌流與內部故障電流精度，具有抗干擾能力。

1 小波包變換

小波包能夠對信號進行更加精細的分析，它將頻帶進行多層次劃分，既具備了小波變換良好的時頻局部化的特點，又對多分辨分析沒有細分的高頻部分進行更深層次的分解，這種分解具有無冗余，無疏漏的特點，因此具有優于小波變換的時頻特性［4］。

利用小波包對信號進行分解時，首先要確定小波函數及分解尺度。由于勵磁涌流與內部故障電流的最大差異在于波形間斷角的存在與否。因此利用小波識別涌流時，關鍵是它檢測信號突變與分析局部時頻信號的能力。所以，選取的小波函數應該具有正交性，消失矩階數較高，以及緊支撐性的特點［5］。綜合多種因素，并借鑒以往的經驗，最終選用coif4小波進行三層小波包分解。二分法思想在小波包分解上得到了采用，每次分解頻帶都被分為兩段，所以直到第3層時，電流信號被劃分為8段。coif4三層小波包分解結構圖如圖1所示。

圖1 三層小波包分解結構圖Fig．1 Decomposition diagram of three-level wavelet packet

三層小波包分解后所得8個子頻帶并不是按順序排列，會產生頻帶交錯現象［6］，正確的排列順序(頻率增大)為(3，0)(3，1)(3，2)(3，3)(3，4)(3，5)(3，6)(3，7)。

信號S經小波包分解i層后，可得到2i個子頻帶，因此可以這樣表示S:

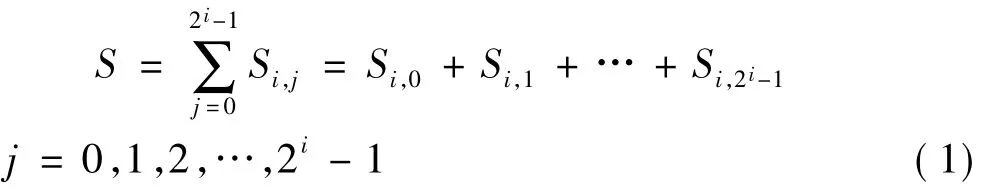
式中 Si，j代表第 i分解層上節點(i，j)的重構信號。

根據Parseval定理及公式(1)，以S(3，j)表示第3層的第 j個子頻帶，則 S(3，j)對應的小波包能量為:

式中E(3，j)即表示S第3分解層上節點(3，j)的頻帶能量，xj，k(j=0，1，2，…，7;k=1，2，…，n)表示重構信號Si，j的離散點幅值，其中，n表示信號采樣點數，即第3層每個節點的小波包系數。

第3層的小波包總能量值為:

引入相對小波包能量的概念，即每個子頻帶占第3層總能量值的比例。為了避免數據過大引起分析計算不方便，取總能量值的根號，即E=

則相對小波包能量為:

因此，小波包能量特征為:

2 改進PSO-PNN

概率神經網絡(Probabilistic Neural Network，PNN)于1989年由D．F．Specht博士首先提出，是由徑向基網絡(Radial Basis Function，RBF)發展而來的一種前饋性神經網絡。不同于傳統RBF的是，PNN是一種專門用于解決模式分類的神經網絡［7］。PNN訓練時間短、不易產生局部最優，而且它的分類正確率較高［8］。

PNN網絡一般由輸入層、隱含層和輸出層三層組成，輸入層由信號源節點組成，隱含層的單元個數取決于針對解決的問題，其結構如圖2所示。

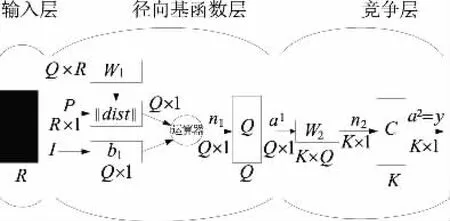
圖2 概率神經網絡結構圖Fig．2 PNN neural network structure chart

圖2中，R為輸入向量的維數，Q為隱含層的神經元個數，K為輸出層的神經元個數，W1表示輸入權重向量，‖dist‖模塊表示輸入向量和權值向量的距離，n1為輸入向量p和權值向量W1的距離乘以閾值b1，模塊C為競爭傳遞函數，它是為了找出輸入向量n2中元素的最大值，則與最大值同一類別的神經元的輸出即為1，其他類別的神經元輸出為0。

雖然相對于其他進化算法，PSO在解決復雜組合優化類問題上有其獨特的優越性，但是不可否認，PSO算法也存在許多缺點，比如搜索精度不高、局部搜索能力差、易陷入局部極小解、對參數有較大的依賴性等。慣性權重能夠提高算法的全局和局部搜索能力［9］，因此粒子群改進策略體現在慣性權重上。為此將慣性權重ω定義為隨迭代次數線性變化，從最大加權因子減小到最小加權因子，即:

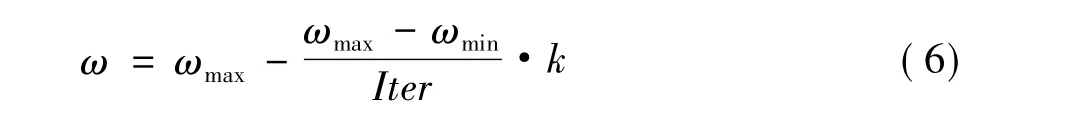
式中ωmax、ωmin分別表示最大、最小慣性權重;k為當前的迭代步數;Iter為總迭代步數。該方法提高了PSO的搜索能力和收斂速度，增強了其性能。

利用改進PSO優化PNN網絡的基本思想是運用改進PSO算法代替PNN網絡的訓練算法來優化PNN網絡參數。PSO的優勢在于簡單容易實現，而且需要調整的參數較少。首先隨機假設一個解，通過迭代的方法尋找最優解，依靠適應度評價解的優良［10-11］。適應度函數f(x)用訓練的誤差表示，計算公式為:

式中p代表樣本的數目;yp是實際輸出值;tp是樣本輸出值。

3 小波包能量特征提取

采用PSCAD/EMTDC仿真軟件建立三相變壓器勵磁涌流及各種內部故障仿真模型，將PSCAD仿真數據導入MATLAB，利用coif4小波分別對勵磁涌流和故障電流信號進行分解重構。選擇AB相差流，勵磁涌流以系統電阻1 Ω、合閘角0°以及鐵芯剩磁0為例，內部故障以2%的匝間故障、A相接地故障、AC兩相接地故障為例，小波包系數如圖3～圖6所示。

對比圖3～圖6，發現勵磁涌流的重構系數一直有較大的數值，且從涌流出現開始一直持續到涌流結束;而內部故障電流(包括匝間故障和各種相間故障)的重構系數幾乎只在故障發生時刻和結束時刻出現，數值比較小。小波系數與電流信號的突變點相對應，因此可以總結，經過小波包分析之后，勵磁涌流有很多的突變點，貫穿涌流出現的整個過程;內部故障電流的突變點很少，只在故障發生時刻和結束時刻存在。

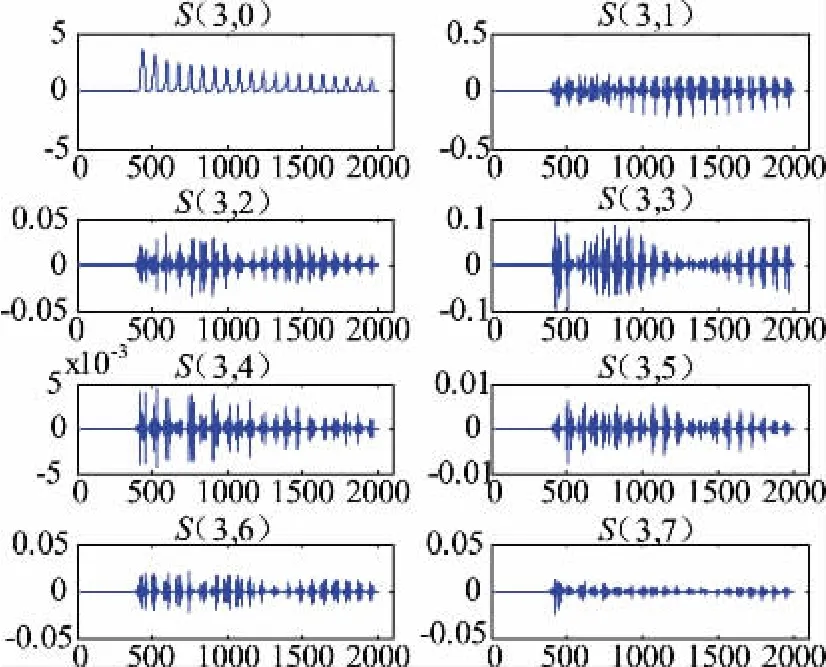
圖3 勵磁涌流的小波包系數Fig．3 Wavelet packet coefficient of inrush current

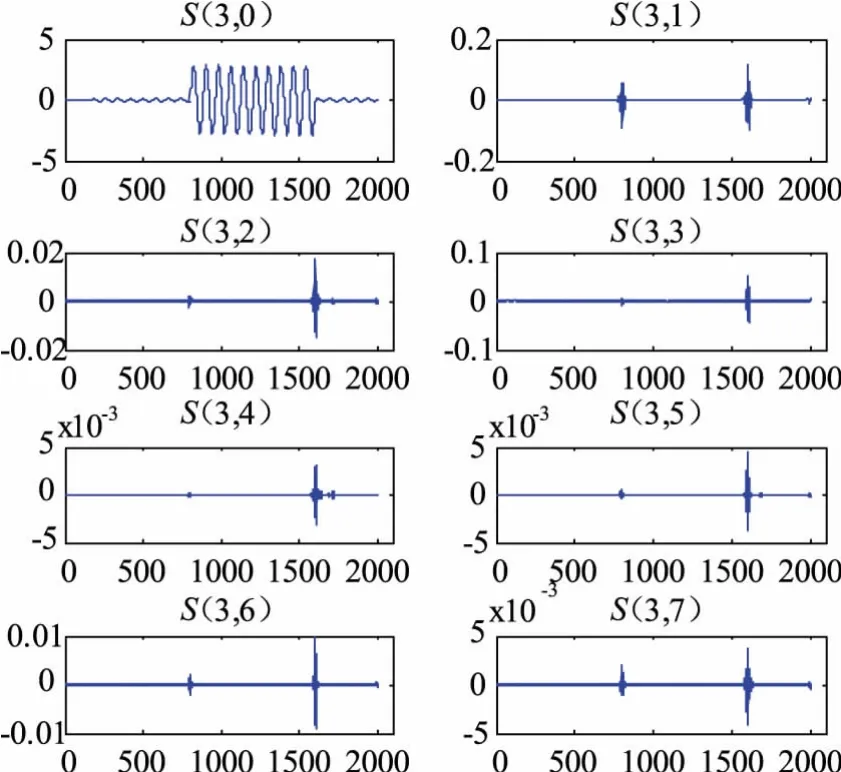
圖4 匝間故障(2%)的小波包系數Fig．4 Wavelet packet coefficient of turn-to-turn fault(2%)

圖5 A相接地故障的小波包系數Fig．5 Wavelet packet coefficient of A phase ground fault

圖6 AC兩相接地故障的小波包系數Fig．6 Wavelet packet coefficient of AC double phase-grounded fault

根據公式(2)～公式(4)計算第三分解層的每個子頻帶的能量值和總能量值，最后根據公式(5)計算小波包能量特征值，最終獲得8個元素組成的能量特征向量。各種故障的AB相差流的小波包能量特征值如表1所示。

表1中，頻率按從小到大，即低頻到高頻的順序，由表1可以發現，去除第一頻段，勵磁涌流的小波包能量值均比內部故障電流大得多。小波包能量值與小波系數是對應的，而小波系數又代表了突變點的數量，上述結論正好表明勵磁涌流的突變點多，而故障電流的突變點少。

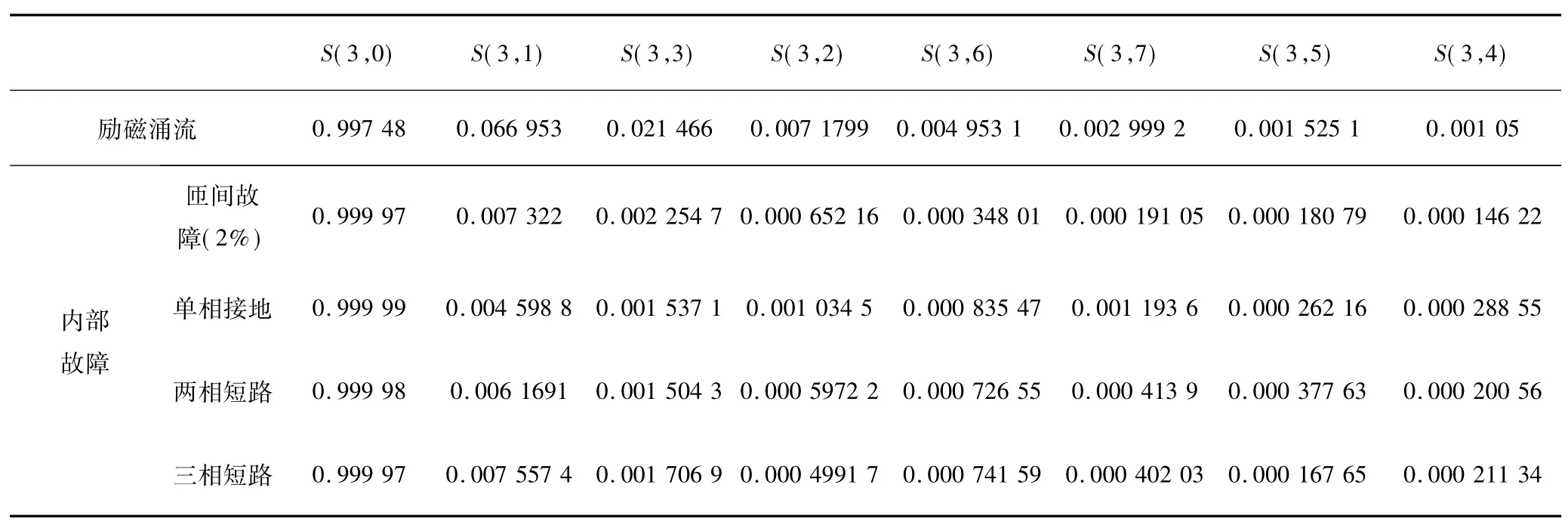
表1 AB相差流的小波包能量特征值Tab．1 Wavelet packet energy feature value of AB phase difference flow

4 改進PSO-PNN識別勵磁涌流

由于每相差流經過小波包分解均可得到一個由8個元素構成的特征向量，因此對于三相系統，一共可獲得24個元素組成的特征向量組。所以，PNN網絡的實際輸入向量即為這24個元素組成的特征向量組。表1中能量特征向量數據均分布在［0，1］之間，所以無需對數據進行預處理，可以直接作為PNN網絡的輸入。隱含層的節點數目需要在實驗仿真中得以確定。PNN網絡的實際輸出向量為1個，設置勵磁涌流的理想輸出值為1，故障電流的理想輸出值為0。PNN網絡的隱含層采用高斯函數作為傳遞函數，輸出層的傳遞函數選擇競爭函數。

樣本包括訓練樣本和測試樣本，為了保證結果的準確性和可靠性，本文考慮了所有的故障類型及各種不同的影響因素。最后一共獲得756組樣本數據，即可得到756組能量特征向量，其中，勵磁涌流樣本252組，故障樣本504組。

本節的目的是利用改進PSO訓練網絡，達到全局最優的目的。對于全局最優值，我們需要確定適應函數，粒子的適應度值是根據分類誤差計算得來。PSO本身并沒有很多的參數需要調整，在仿真實驗中我們只需要調整隱含層的節點數目以取得較好的分類效果。通過實驗，隱含層節點數與分類誤差的關系如圖7所示。

由圖7可以看出，當隱含層節點數等于10時，所測得誤差最小，為9．7861e-6，代表此時PSO優化訓練網絡的逼近能力最強。PSO中，最優參數的獲取過程其實就是尋找全局最優值。全局最優值的適應度值隨PSO迭代的變化曲線如圖8所示。

圖7 隱含層節點數與分類誤差的關系Fig．7 Relation between classification error and the number of hidden neurons

圖8 適應度值的變化曲線Fig．8 Curve of fitness value

從圖8可以看出，全局最優值的適應度值隨迭代次數的變化逐漸減小，當迭代次數大于10次時，適應度值基本上不再改變，證明此時達到目標誤差，訓練得到收斂。

由以上分析可知，PNN網絡的結構確定為“24-10-1”。接下來利用改進的最優PSO算法來優化PNN網絡，進行訓練測試，并對該網絡的運行性能、實際的輸出結果以及誤差進行綜合分析。

為了突顯該網絡的優越性，利用同樣的樣本對改進的BP神經網絡進行訓練，將其與改進PSOPNN網絡進行對比。首先，隨機選取504組訓練樣本(包括168組勵磁涌流樣本和336組故障樣本)，分別對以上兩種網絡進行訓練，結果如圖9和圖10所示。

由圖9和圖10可以看出，改進PSO-PNN網絡僅通過9步訓練就達到了誤差精度，而改進型BP網絡需經過156步訓練才滿足誤差精度。這表明改進PSO-PNN網絡訓練性能很好，收斂更快，能夠在最短時間內搜索到最優值。

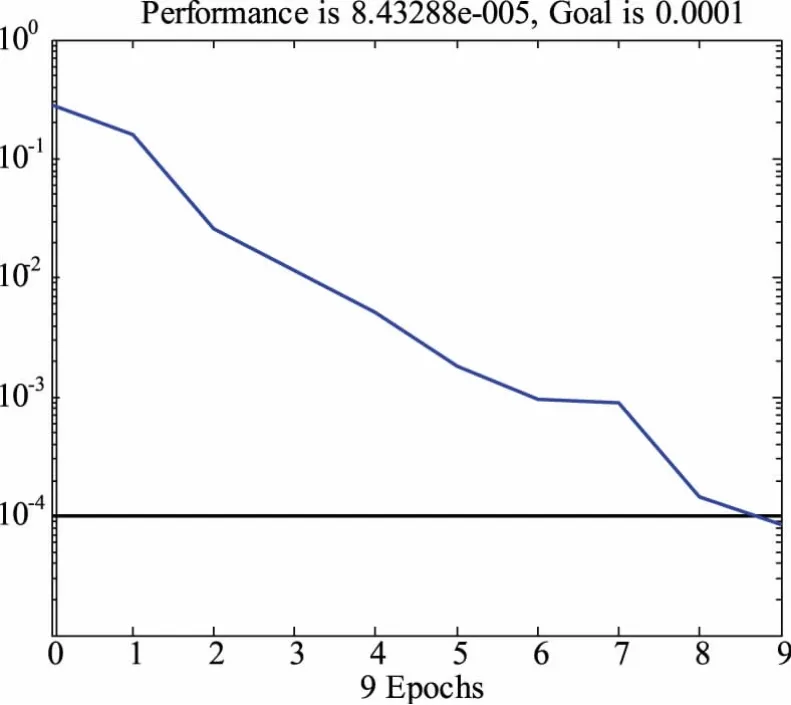
圖9 改進PSO-PNN網絡的訓練曲線Fig．9 Training curve of improved PSO-PNN network

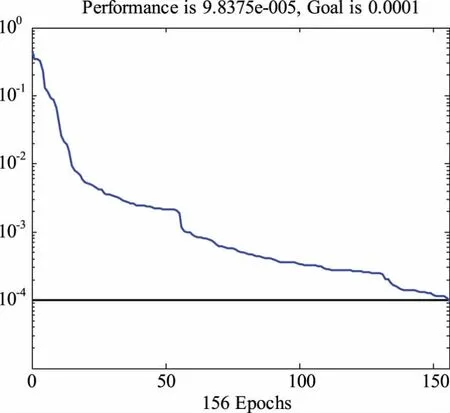
圖10 改進型BP網絡的訓練曲線Fig．10 Training curve of improved BP network

然后運用504組訓練樣本對改進PSO-PNN網絡訓練并進行誤差計算。網絡的實際輸出與期望值的逼近圖和兩者的誤差分布圖，分別如圖11和圖12所示。

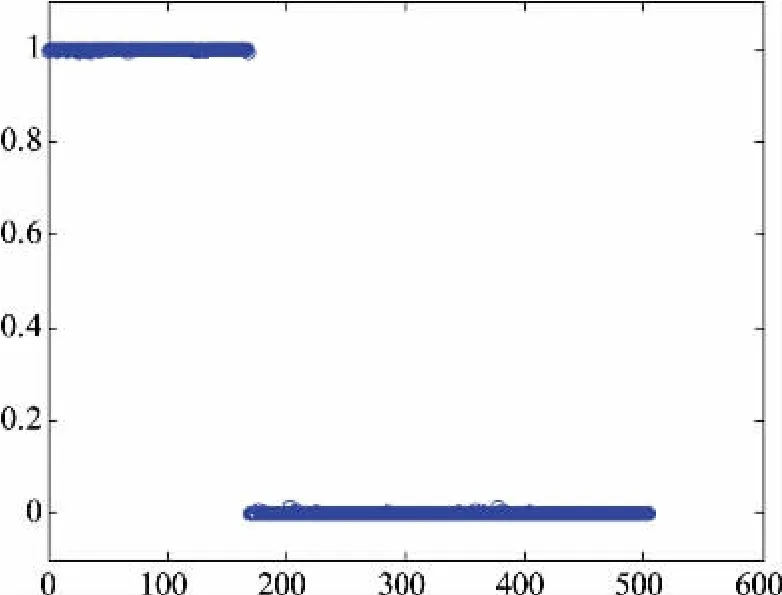
圖11 訓練樣本的實際輸出與期望值逼近圖Fig．11 Approximation chart of actual output and expectation of training samples

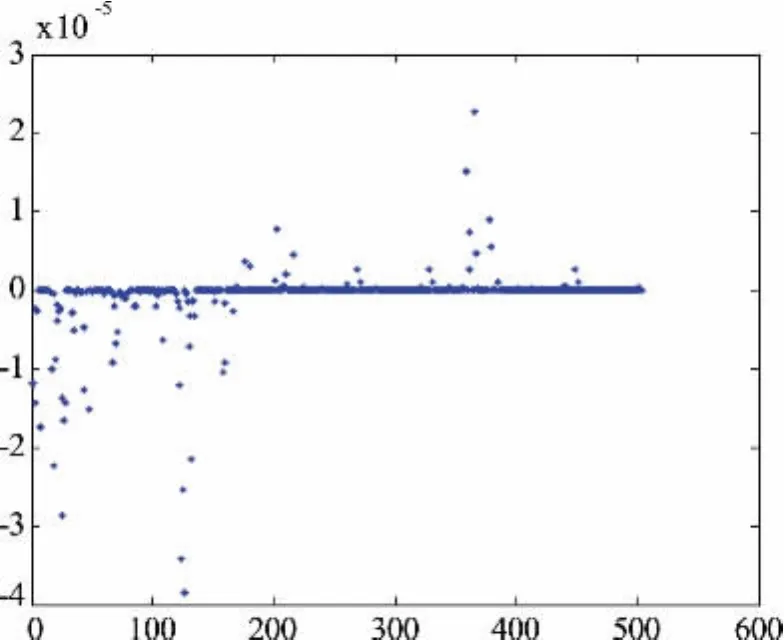
圖12 訓練樣本的誤差分布圖Fig．12 Error distribution chart of training samples

從圖11和圖12可以看出，504組訓練樣本對改進PSO-PNN網絡的訓練性能達到了預期要求，訓練誤差在［－4e-5，3e-5］變化，均在目標誤差范圍內。

最后利用252組測試樣本(包括84組勵磁涌流樣本和168組故障樣本)對該網絡進行測試，樣本的實際輸出結果如圖13所示，實際輸出與期望輸出值的誤差分布圖如圖14所示。

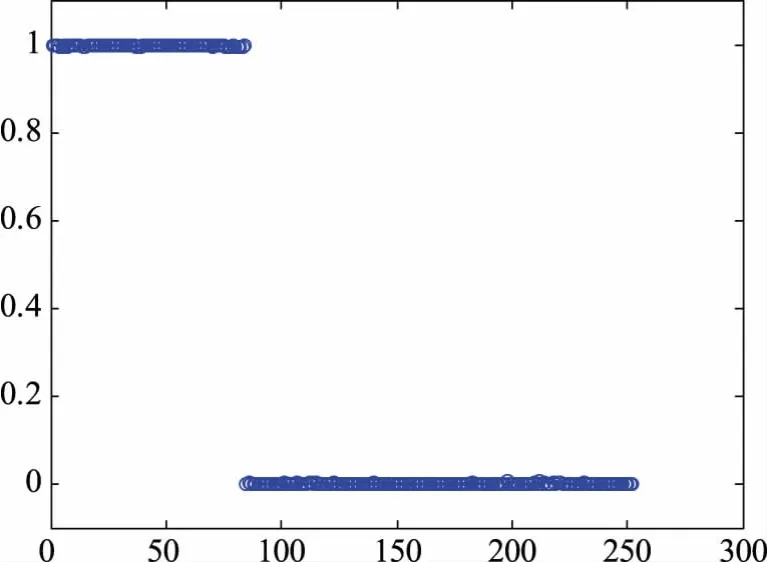
圖13 測試樣本實際輸出與期望值逼近圖Fig．13 Approximation chart of actual output and expectation of test samples

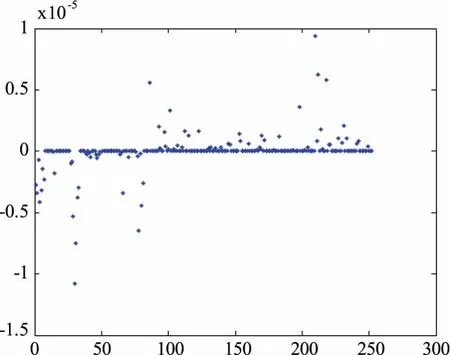
圖14 測試樣本誤差分布圖Fig．14 Error distribution chart of test samples

由圖13和圖14可以看出，252組測試樣本對改進PSO優化后的PNN網絡的訓練同樣達到了預期要求，實際輸出值與期望值十分接近，測試誤差更小，在［－1．5e-5，1e-5］內變化，均在目標誤差范圍內。

勵磁涌流的理想輸出值為1，故障電流的理想輸出值為0。圖11中的勵磁涌流樣本的輸出均在1附近變化，圖13的故障樣本的輸出均在0附近變化。為了增加可靠性，保留一定的裕度，設置上下0．1的裕度。由于輸出值在［0，1］之間，因此，提出以下判據:

(1)當網絡的實際輸出在［0．9，1］之間變化時，確定為勵磁涌流;

(2)當網絡的實際輸出在［0，0．1］之間變化時，確定為內部故障。

5 結束語

優化問題主要包括兩個方面:一是要尋找全局最優點;二是要求有較高的收斂速度。經過以上實例仿真分析，可見改進PSO優化PNN網絡既能在最短時間內搜索到全局最優值，又可以快速地達到收斂。綜上，此算法的優化性能較強，網絡的分類模型精度較高，保護具有較高的可靠性。