穩健估計在豐都河北大橋變形監測中的應用
徐金鴻,孫迅文
(1.重慶交通大學 土木工程學院,重慶 400074;2.重慶交通大學 研究生院,重慶 400074)
測量過程中存在粗差,若采用最小二乘估計極有可能使得估計值偏離真值,而在變形監測過程中,控制網的精度要求較高,因此,在控制網的平差過程中采用穩健估計可將粗差剔除,從而使得控制網的可靠性提高,更能滿足變形監測的需求。豐都河北大橋唯一進城通道,車流量大,在回填過程中回填拆除會對橋體造成影響,易使橋體垮塌,需對該橋進行變形監測。考慮到監測過程中的靈敏性,對控制網的要求較高,采用穩健估計對控制網及布設的監測點進行平差。
1 穩健估計
1.1 概 述
穩健估計是在粗差不可避免的情況下,選擇適當的估計方法,使參數的估值盡可能的避免粗差的影響,得到正常模式下的最佳估值[1]。從數理統計角度來說,當要計算某個或某些統計量T的值時,其值是由樣本X1,X2,…,Xn所決定的。
由于在獲得觀測樣本X1,X2,…,Xn過程中,可能由于儀器故障或者觀測疏忽及記錄錯誤等使得X1,X2,…,Xn中的一個或幾個包含了較大的誤差,稱為過失誤差或粗差。一兩個數據的錯誤可能導致整個統計分析結果完全改觀。因此,可把具有這種性質的統計量T或者統計方法稱為穩健性。傳統的統計方法:樣本均值、樣本方差、最小二乘估計等往往是不具穩健性的,因而在實際應用中也是具有潛在不安全因素的。
穩健估計基本可分為3大類,即M估計,也稱為極大似然估計;L估計,也稱為排序線性組合估計;R估計,也稱為秩估計。但在測量平差中主要采用的估計準則為M估計。
設p(x)為一個定義在(-∞,+∞)上函數,使(-∞,b]非增,在[b,+∞]非降。若統計量Tn=Tn(X1,X2,…,Xn)滿足條件[2]
.
(1)
則稱Tn為位置的一個M估計。滿足上式的Tn可能不唯一,但當p在(-∞,+∞)上處處連續,則Tn必存在。當p′=φ存在時,改寫為

φ(Xi-Tn)=0.
(2)
只有當p為凸函數且p在(-∞,+∞)上處處存在時,式(1)和式(2)等價。
在以M估計為準則下計算簡單,公式簡明,且易于編程實現的選權迭代法在測量平差中廣為應用。故在豐都河北大橋變形監測控制網平差中采用的是選權迭代法。
1.2 選權迭代法
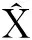
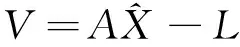
(3)
按穩健最小二乘估計原理,參數的解向量為
(4)
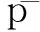
(5)
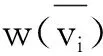
(6)
其中,取k0=1.5,k1=2.5。
由于vi是參數X的函數,只能在X計算后才能獲得,故抗差估計只能以迭代形式完成。設X0為參數估值迭代解的初始值,則有
(7)
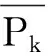
ε.
(8)
時,停止迭代即得到參數的估值。其中ε為設定的收斂條件。
且參數的權逆陣為
(9)
單位權中誤差為
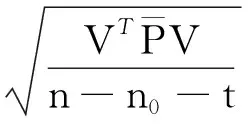
(10)
式中:n0為權重為零的觀測值個數。
2 算例及分析
2.1 基準網概況
該基準網為包含3個控制點的單三角網,點位均遠離變形監測區域,如圖1所示。
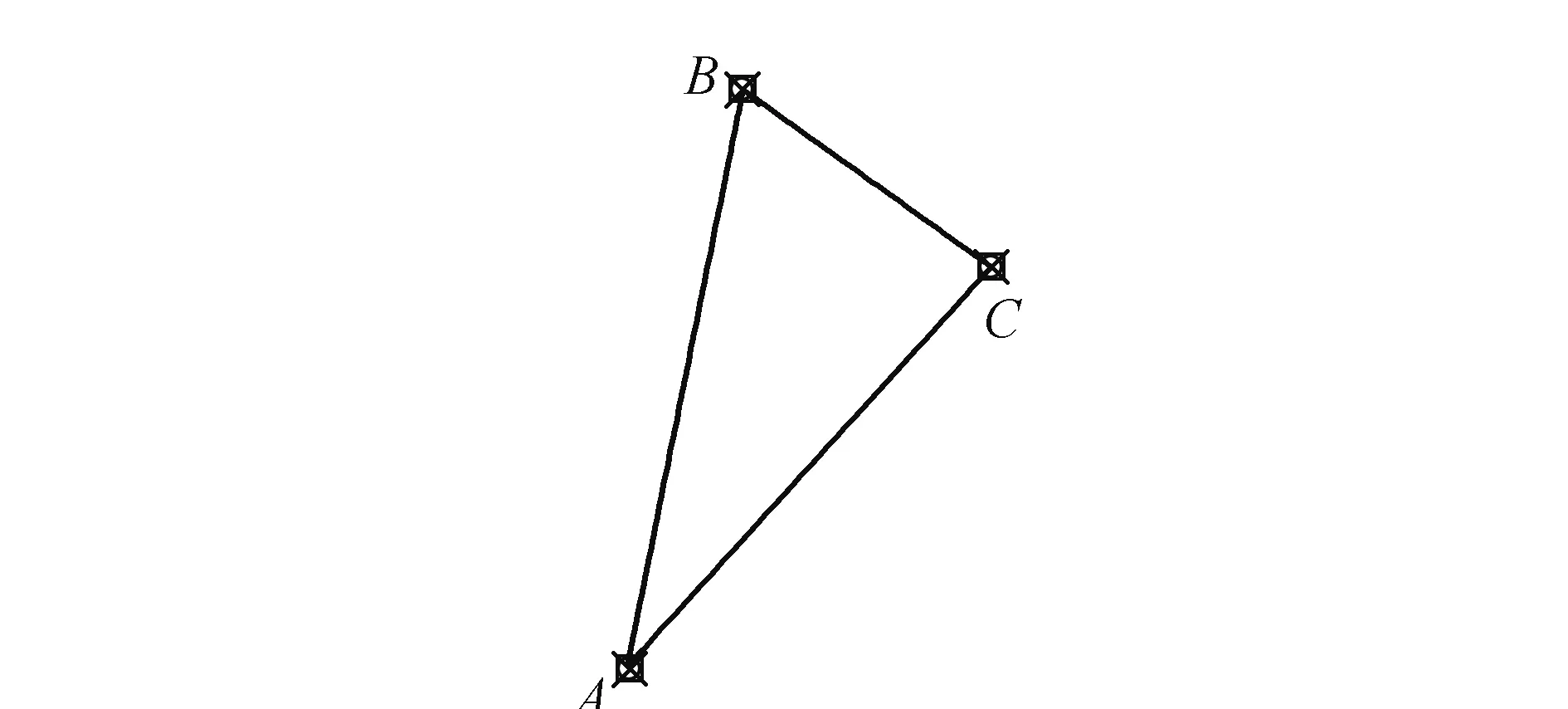
圖1 基準網形
反映橋軸線方向的位移變化,以橋軸線為X方向建立測量坐標系,C點為已知點其坐標為(1 000,1 000),且AC邊方位角為(124°22′46.13″),并以此為基準建立該橋平面獨立監測坐標系。
采用徠卡TS30對基準網進行測邊測角,儀器測角精度為0.5″,測距精度為1 mm+1 ppm,共計9個測回。其中,每測回均進行限差檢核,半測回歸零差及測回互差均為6″。整理后的每測回觀測數據如表1和表2所示。基準網采用間接平差方式對每個觀測值列立誤差方程式進行整體平差,以下為詳細平差結果及分析。
分析穩健估計在平差處理過程中的實現機制,并驗證其在工程實踐應用中是否有效,分別按最小二乘法和穩健估計兩種平差方法進行平差,表3為平差結果,其中μ為單位權中誤差,x,y分別表示平差后橫、縱坐標,而dx為坐標平差值中誤差。
從表3中可明顯看出兩種平差方法所得單位權中誤差、平差坐標及平差值中誤差的結果完全一致。分析產生該結果的主要原因為觀測值數據質量較好,并不存在觀測粗差。從數學原理來說,在無粗差情況下,兩種方法本無本質區別,因為兩者均是在最小二乘準則下進行的平差,故可斷言在無粗差情況下,兩種方法將獲得一致性平差結果。
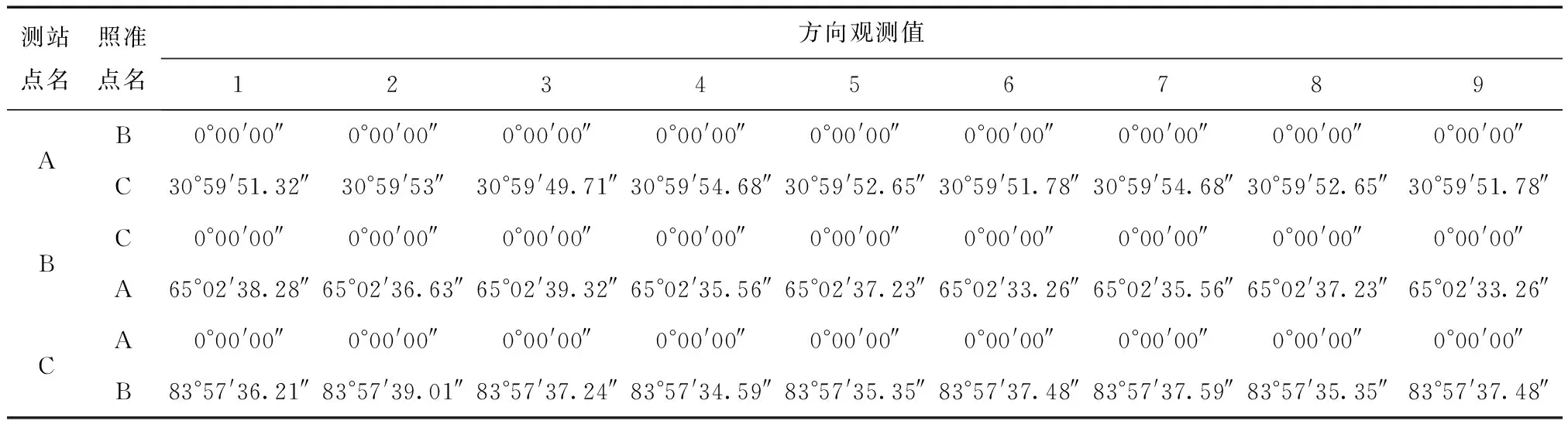
表1 方向觀測值

表2 邊長觀刪值 m
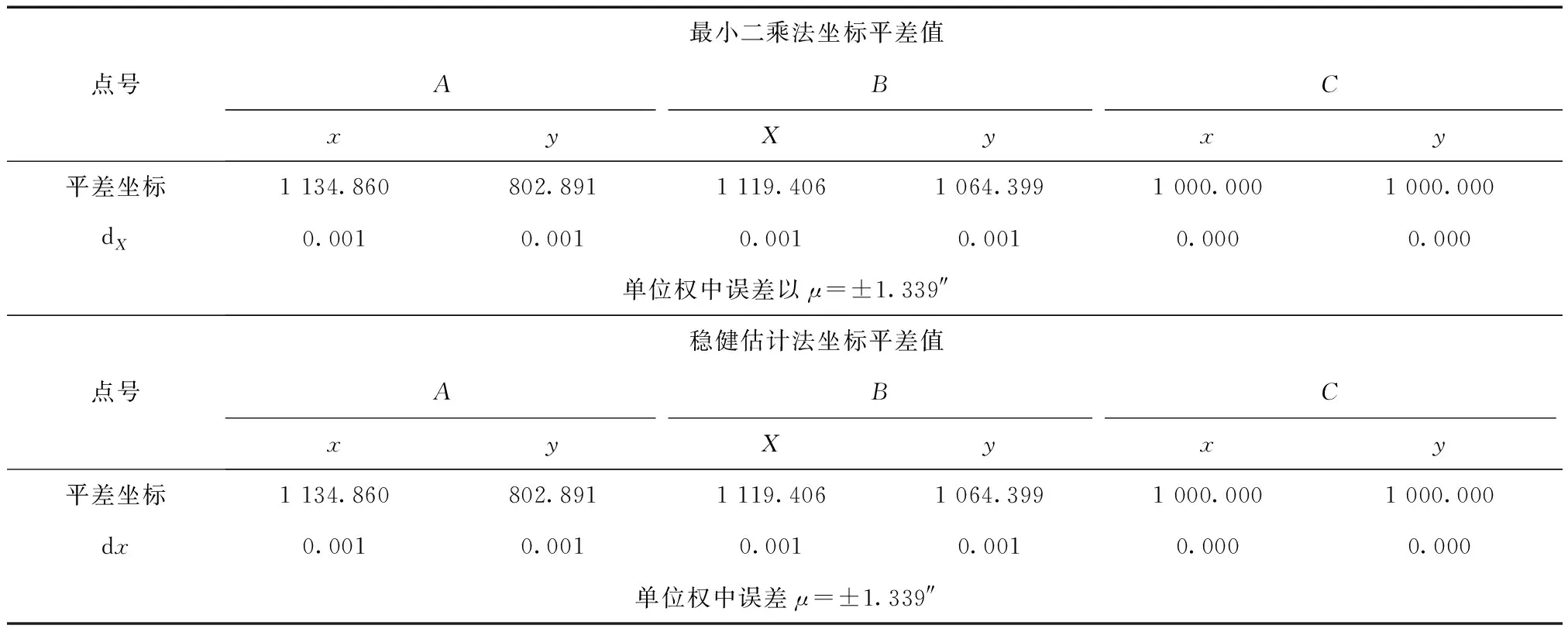
表3 平差結果 m
2.2 監測網概況
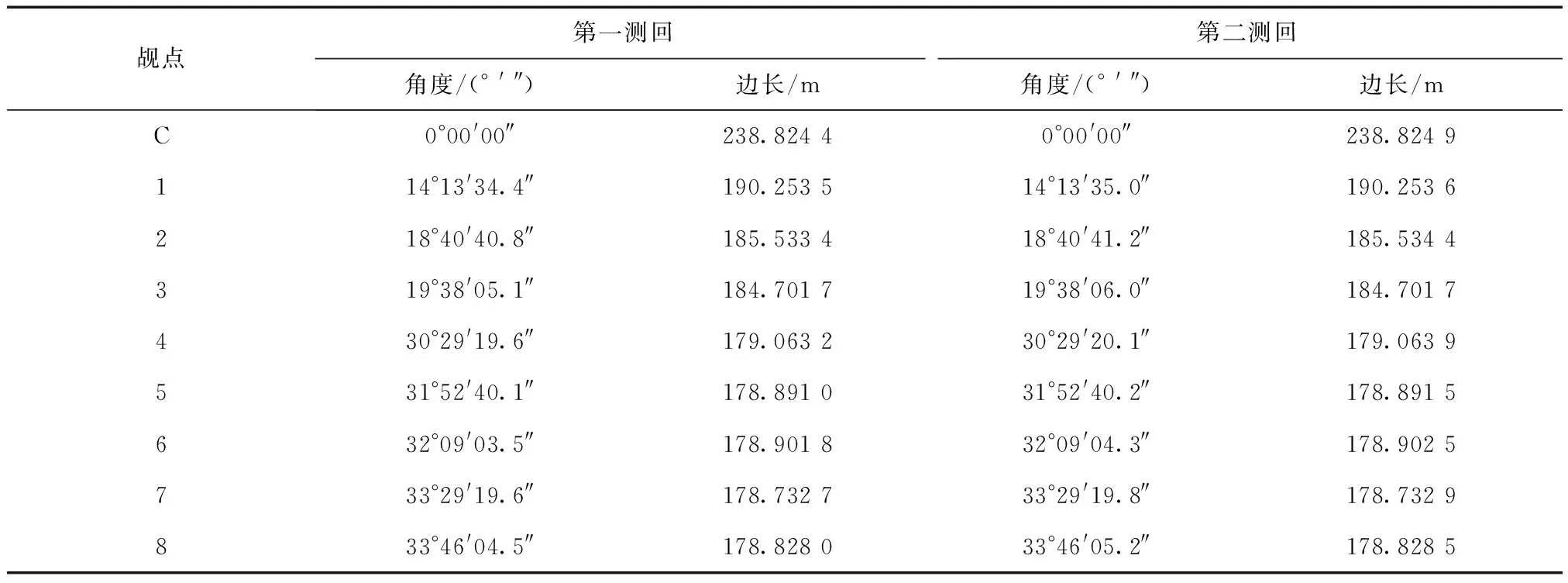
監測橋位移變化,在拱圈布設了8個監測點,并與基準網點共同構成參考網。采用方向觀測法進行角度、距離測量,共計6個測回,每測回均進行限差檢核,半測回歸零差及測回互差均為6″,如表4所示為部分整理后的每測回觀測數據。
通過每測回觀測數據,對參考網進行坐標平差得到每期監測點位的坐標平差值,即可用于該橋的變形分析。
2.2.1 監測網平差結果
同樣,對每個觀測值列立誤差方程式,仍按穩健估計和最小二乘估計對監測網進行整體坐標平差處理,平差結果如表5所示。
從表5可清晰看出,最小二乘估計下的單位權中誤差遠大于穩健估計下的單位權中誤差,且其值遠超出合理范圍,再從平差值中誤差來看,也表現出了異常性,因此可判斷某些觀測值存在粗差。最小二乘估計不具穩健性,在有粗差的情況下,所得單位權中誤差過大,坐標平差值中誤差反常,均呈異常狀態,因此在該種情況下所得平差結果是不可靠的,嚴重偏離了參數真實估值的。反之,在穩健估計準則下,盡管觀測值存在粗差,但通過對其進行屏蔽或者部分信息使用,依然能夠獲得較為可靠的平差結果。證實了在粗差存在情況下,穩健估計的確是一種優于最小二乘估計的方法,因此將穩健估計應用到實際的工程平差處理中,是一種能提高平差結果可靠性的有效手段。接下來,為探究穩健估計對觀測值的處理情況,現對觀測值殘差及等價權因子進行分析。
表4 水平角及邊長觀測值(方向觀測法)測站A
覘點第一測回第二測回角度/(° ' ″)邊長/m角度/(° ' ″)邊長/mC0°00'00″238.824 40°00'00″238.824 9114°13'34.4″190.253 514°13'35.0″190.253 6218°40'40.8″185.533 418°40'41.2″185.534 4319°38'05.1″184.701 719°38'06.0″184.701 7430°29'19.6″179.063 230°29'20.1″179.063 9531°52'40.1″178.891 031°52'40.2″178.891 5632°09'03.5″178.901 832°09'04.3″178.902 5733°29'19.6″178.732 733°29'19.8″178.732 9833°46'04.5″178.828 033°46'05.2″178.828 5
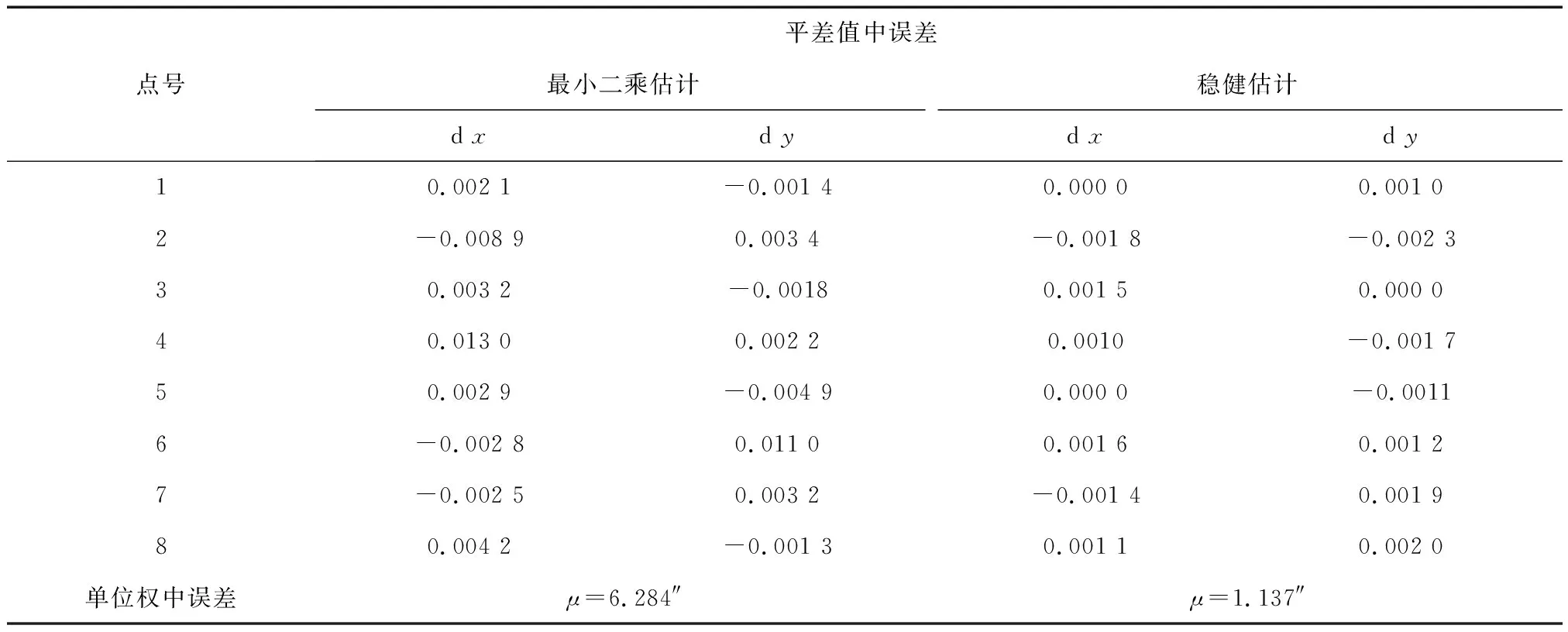
表5 監測點平差結果 m
2.2.2 觀測值殘差分析
如圖2所示,其中黑色曲線表示最小二乘平差后的觀測值殘差,紅色表示穩健估計平差后的觀測值殘差,橫坐標表示按順序對觀測值依次編號。從圖可清晰看出兩種方法下所得殘差基本一致,且在16、28號方向觀測值及10號邊長觀測觀測值均出現了較大殘差異常。這表明在這幾個觀測中出現了較大粗差,但因最小二乘估計不具有穩健性,即不對殘差異常值進行任何處理,這勢必將粗差引入到參數估值中,導致結果嚴重偏離真值,而穩健估計對粗差具有抵抗性,因此對具有粗差的觀測值進行棄用或者部分信息的使用。
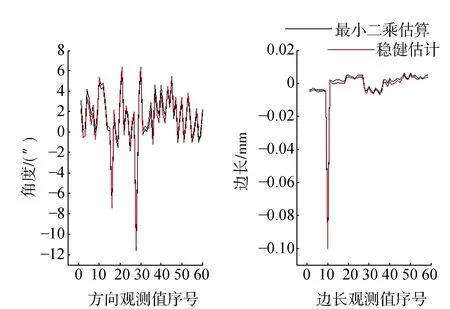
圖2 觀測值殘差
2.2.3 等價權因子分析
穩健估計中,等價權因子的大小直接反應了對觀測值的使用情況,即等于零的等價權因子所代表的觀測值存在粗差,該觀測值不參與平差,大于0小于1代表部分利用觀測值信息,等于1則表示無粗差。按穩健估計進行平差,如圖3所示為各觀測值等價權因子情況。
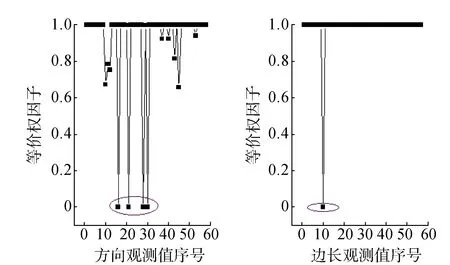
圖3 等價權因子
從圖3上可清晰反映出16、21、28、30號方向觀測值及10號邊長觀測值權重均為零(圖中紅色標記),即這幾個觀測值并不參與平差,而是通過調整權重方式被棄用,也即達到了抵抗粗差的目的。但也看到一些權因子的范圍在(0 ,1)之間,這說明了在粗差存在情況下,是有可能存在損失一些效率的風險的,盡管如此,抗差估計有效地規避了粗差的有害影響,獲得了較為可靠的參數估值。
3 結 論
1)從兩種方法的平差結果來看,若觀測數據不存在粗差,則最小二乘估計和穩健估計在平差結果上將完全一致。
2)若觀測值含有粗差,按最小二乘平差法必將導致粗差被引入,使得平差結果不能反映真實值情況,相反,若按穩健估計進行平差,則可有效地抵御粗差影響,將粗差進行限制,合理利用有效信息,屏蔽無效信息,得到較為可靠的、平差結果。
因此,從該工程實踐來看,將穩健估計應用到平差處理中,提高平差結果的可靠性,避免粗差影響準確。為變形監測提供了可靠的基準及監測成果。因此,穩健估計是一種能夠有效抑制粗差,可提供可靠的平差結果的方法,無論粗差是否存在,
均可獲得最優無偏估值。考慮到粗差的存在具有不可預知性,故在大量的觀測值中若采用最小二乘法進行平差,將導致平差結果失真的可能性變大。

