語音情感分析與仿真

曹維祥

六安職業技術學院信息與電子工程學院，六安, 237158

1 相關研究

人類的聲音含有喜怒哀樂等情感成分，提取語音情感的時域特性和頻域特性，通過計算機分析情感的特性參數，對情感進行辨認，可識別發音人的情緒狀態。未來基于聲音的人機自然交互界面是人機交互的重要方向，實現人機自然交互的前提是提升計算機的語音情感分析與識別能力，這也是現代計算機的人工智能和人機情感交互研究方向，具有廣闊的應用前景[1]。

20世紀70年代，Williams進行了一系列語音情感實驗探索，發現人的語音基音外框形狀變化受控于心理情緒轉變，這是最早的語音情感研究之一[2]。20世紀90年代初，美國MIT下屬的Media Lab在多媒體實驗室開發了“情感編輯器”。21世紀初，馬里博爾大學的Vladimir Hozjan開始探究不同語言的情感分析[3]。2009年4月，新型號“HRP-4C”女性機器人在日本誕生，該機器人可以做出大量不同表情。這種類型機器人可以通過對主人語音指令的判斷分析，表現出高興、憤怒、驚奇、哀傷等表情與主人互動[4-5]。

國內語音情感的計算分析起步較晚，趙力等人于21世紀初進行了情感語音的研究并發表了一系列的研究成果[6]。2003年，中國科學院自動化研究所牽頭主辦了中國首屆有關情感分析與人機交互的交流學習會議。浙江大學人工智能研究所、中國科學院語言研究所、清華大學人機交互與媒體集成研究所以及國家重點模式識別實驗室等國內大型研究院與科研機構都在該領域取得了一定的研究成果。由于漢語的表達方式多樣、中國傳統文化的文化特征和民族性格較為含蓄等原因，中文語音情感分析仍然需要作更深一步的探索發掘。

2 語音情感分類與特征參數

2.1 語音情感分類

目前，國際上還未建立一個公認的模板來區分人類情感，各國研究者都有自己的分類標準，但心理學家通常把人類的高興、悲傷、害怕和憤怒歸為最原始的情感。Scherer教授通過研究認為，說話人的心理變化導致情感語音的變化，人們的發音習慣、說話方法源于社會引導養成[7]。當下大多數學者主要還是借鑒心理學家的研究成果，理論模型有基本情感論和維度空間論等，維度空間論又包括二維情感論和三維情感論[8]。

基本情感論認為，人們的情緒中包含純樸和混雜的成分，這與現代心理學研究內容契合。現代心理學認為，情感都可看成由各種相互獨立的基本情感因子按照某種規則排列組合而成。不同研究者對情感類型的劃分差別很大，表1為目前不同學者對基本情感的分類。

2.2 語音情感特征提取

語音情感的特征參數可選取語音信號的聲學特性、時域和頻域特性。本文選取CASIA語料庫中憤怒(angry)、害怕(fear)、快樂(happy)、悲傷(sad)四種情感，每種情感類型共有10條語料，其中發音人Liu Chanhg和Zhao Quanyin各5條，分別提取這40條情感語音中的每條語音的發音持續時間、單位時間下音節的發出速度、基音周期的最大值和平均值、短時過零率、語音信號第一個共振峰的最大頻率和短時能量的平均值、最大值等8個特征參數，再依次分析不同類型情感語音的每種參數，對比它們相互間的差別。分析語音信號時，噪聲或干擾會影響到語音信號的處理。本文通過預加重處理、信號的分幀和加海明窗函數等方式對語音信號進行預處理[16]。

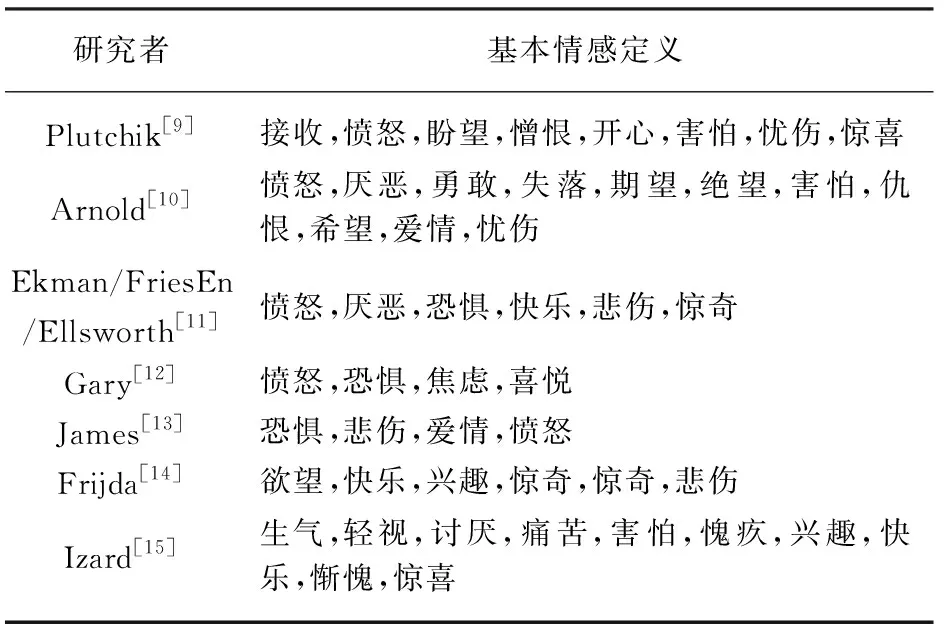
表1 基本情感分類列表

情感語音信號的時間構造研究通常包括語音持續時間和單位時間內發音速度，發音持續時間即該段語料的時間長短，單位時間發音速率即平均每秒發出音節個數[17]。日常生活中，人們可以明顯感覺到人處于不同情感時，說話的時間長度和某個音節發出的速度不同，造成同一句話有不同的斷句方法，因此就要剖析情感語音在時間方向上的構造。通過對40句語料的逐一記錄分析，得到表2的平均發音速率和平均發音持續時間統計表。

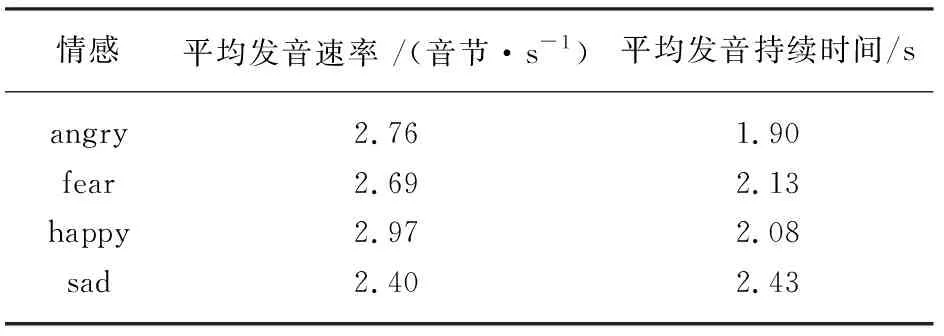
表2 平均發音速率和平均發音持續時間表

由表2可知，4種情感中happy的平均發音速率最快，sad最慢，angry和fear的平均發音速率較為接近；發音時間是sad持續最長，angry最短，fear和happy較為接近。

基音頻率就是聲帶產生共振的頻率，本文利用自相關函數在時域上提取基音周期[18]。對于一個離散語音信號x(n)，其自相關函數可定義為：

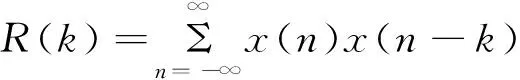
(1)

但語音信號并非一個平穩信號，可利用短時自相關函數來處理。短時自相關函數就是在某個采樣點n的周圍利用窗函數選取部分信號進行自相關計算，即：

(2)

圖1為基音提取，統計周期的最大值和平均值如圖2。由圖2可發現，angry情感的基音周期最大值最高而平均值較小，fear和sad情感的基音周期的最大值和平均值都較接近，happy情感基音周期最大值最低，但平均值最大。顯然，僅通過基音周期分析，fear和sad這兩種情感難以辨別。

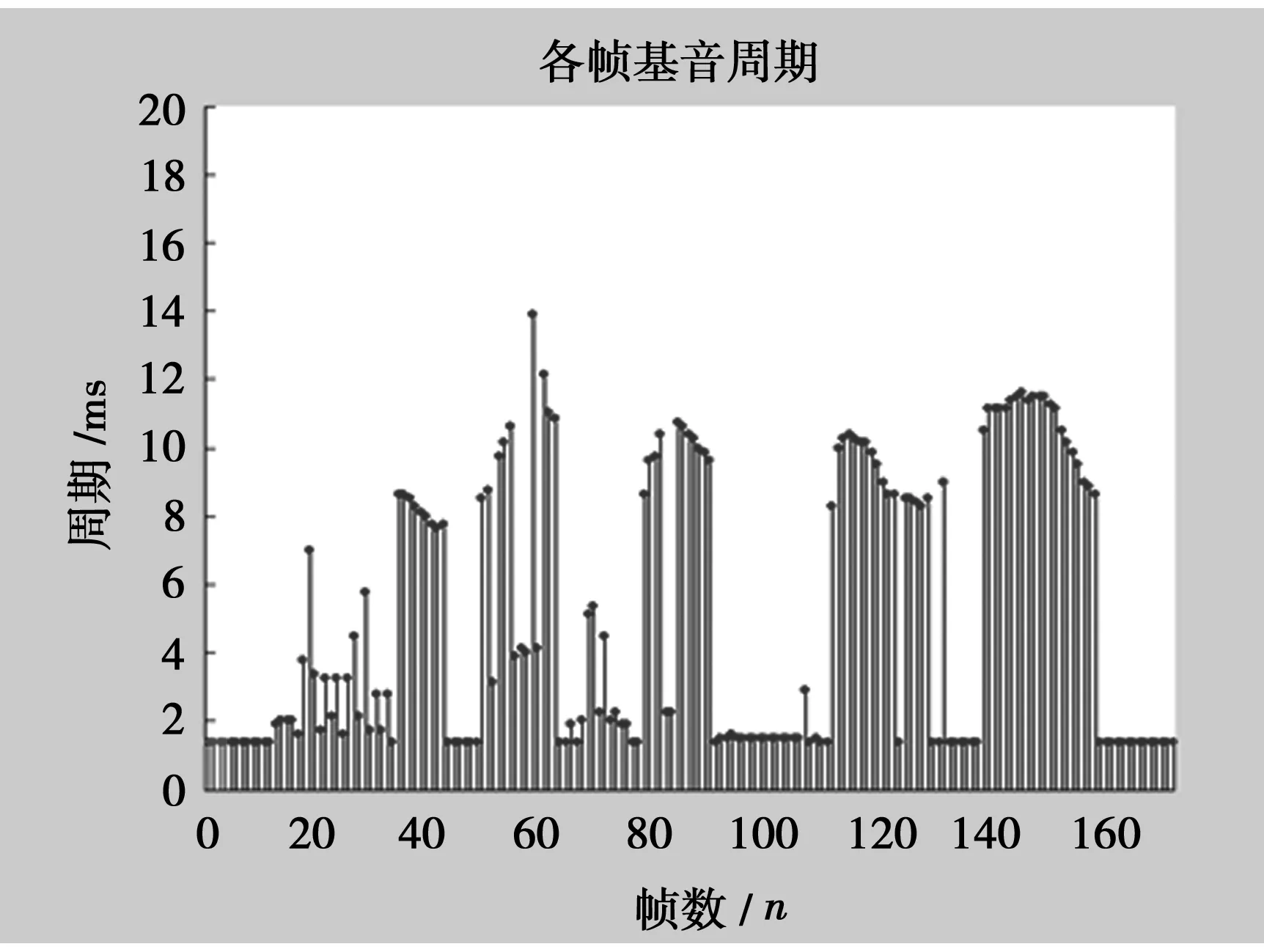
圖1 基音周期提取

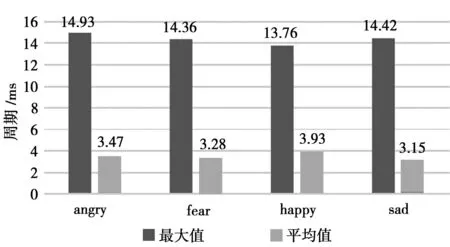
圖2 基音周期的最大值和平均值

生活中人們在發怒時通常聲音較大，哀傷時聲音較小，聲音的大小和聲音的能量與振幅相關，因為時間發生變化時語音信號的能量也隨之改變。描述語音的這種特征變換，需要對短時能量的變化幅度進行探究。對于n時刻下的短時平均能量En可定義為：

(3)

其中N為加窗函數長度，短時能量就是對單位采樣點值的加權平方求和，當窗函數為矩形窗時：

(4)

短時能量提取如圖3，顯示了能量幅值隨時間變化的情況。圖4和圖5分別為Liu和Zhao作為信號的短時能量統計，分析發現：angry情感下，短時能量的平均值和最大值都遠遠高于其他情感，happy情感的短時能量相關數值為第二高，fear和sad兩種情感比較接近，無法辨別。

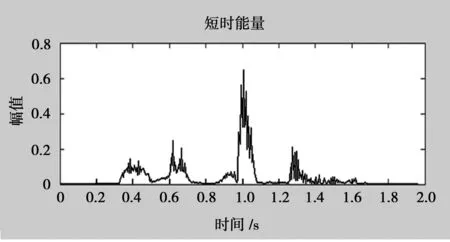
圖3 短時能量提取

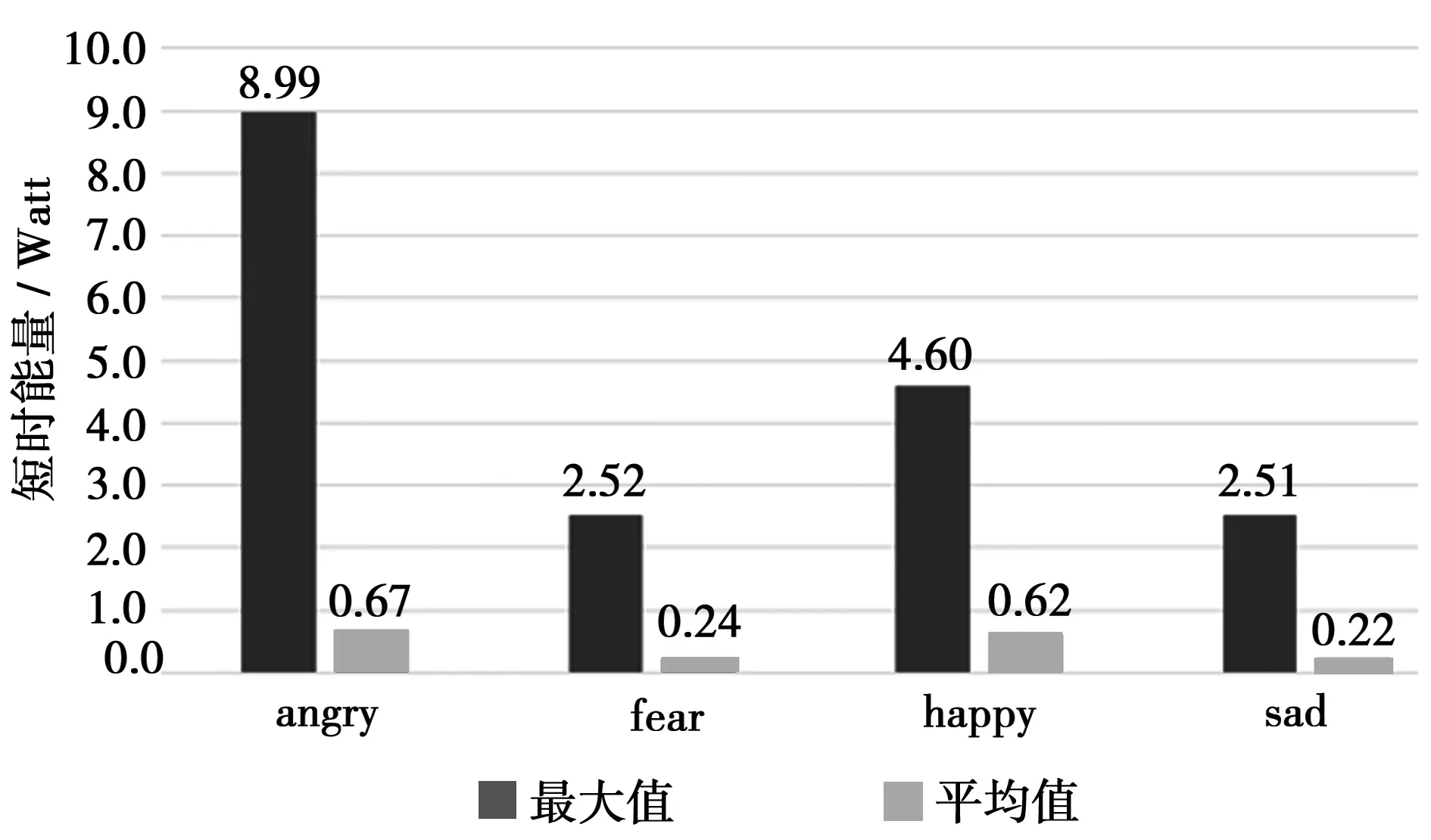
圖4 短時能量圖(Liu)

圖5 短時能量圖(Zhao)

情感語音包含清音與濁音，利用能量檢測，區分濁音效果比較理想，利用短時過零率輔助辨識清音較為理想。語音信號中的高頻段區域和低頻段區域有不同的過零率，通常波形頻率較高的通過橫軸(零電平)次數就越多。對離散時間語音信號來說，只要兩個連續采樣點的數學符號發生了極性變化，就稱為發生了過零過程，短時過零率就是語音信號在某個時間內通過橫向坐標軸的次數。短時平均過零率的定義為：

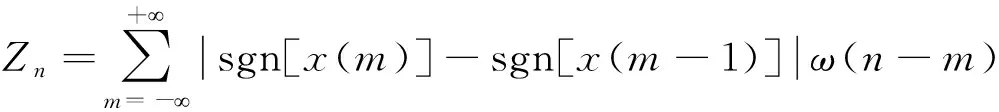
(5)

ω(n-m)的非零值范圍為n-m≥0 ，即n-m≤N-1，故m≥n-N+1

(6)

式中，sgn[ ]是符號函數：

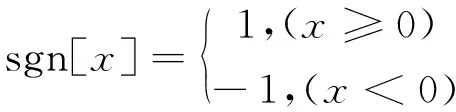
(7)

短時過零率仿真結果如圖6，可以清楚地看到采樣信號各幀的平均過零次數。所得數據分制表后如圖7。從圖7看出fear情緒的短時過零率最高，happy情緒和angry情緒的短時過零率較為接近，sad最低。

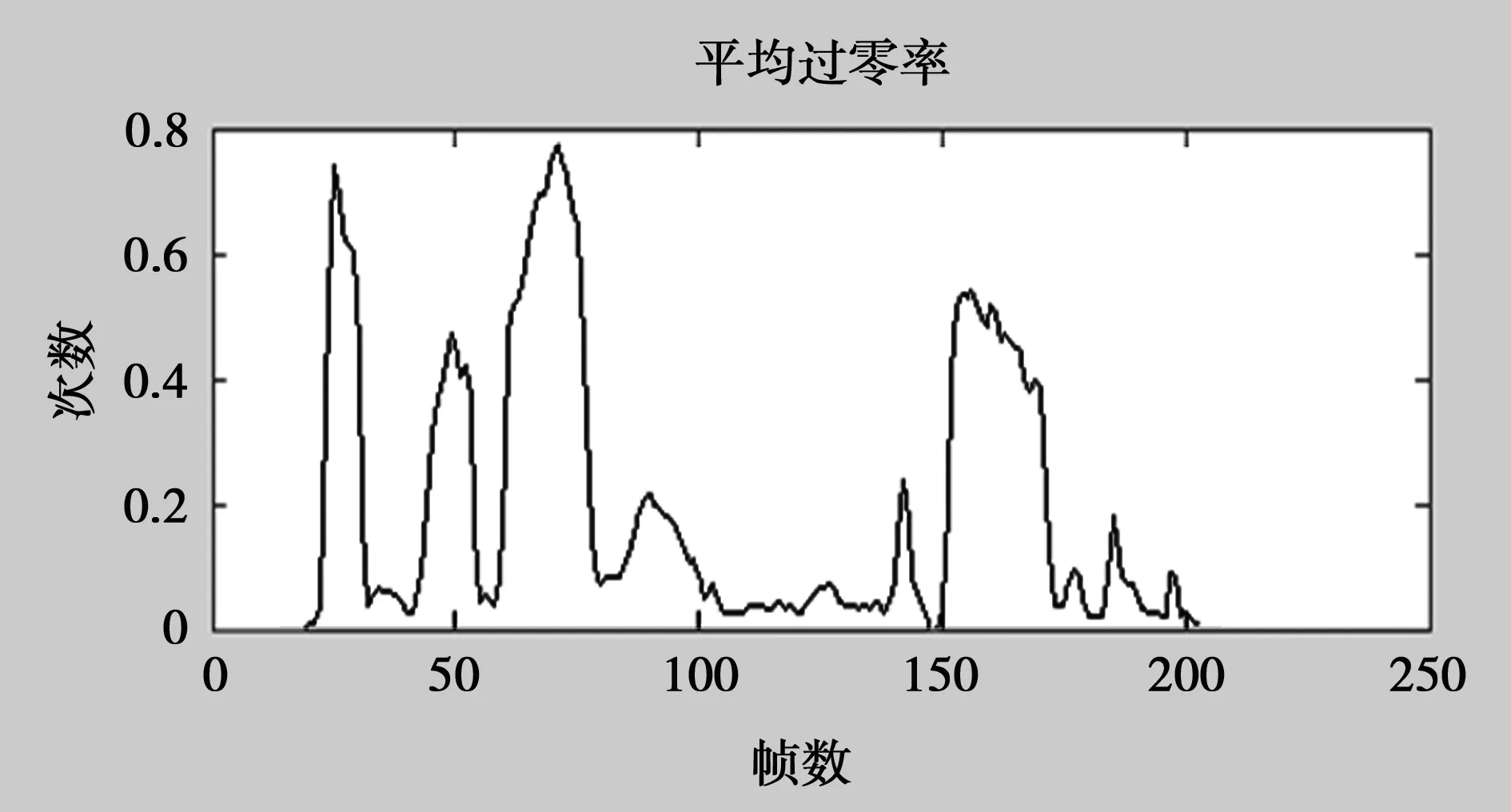
圖6 短時過零率提取

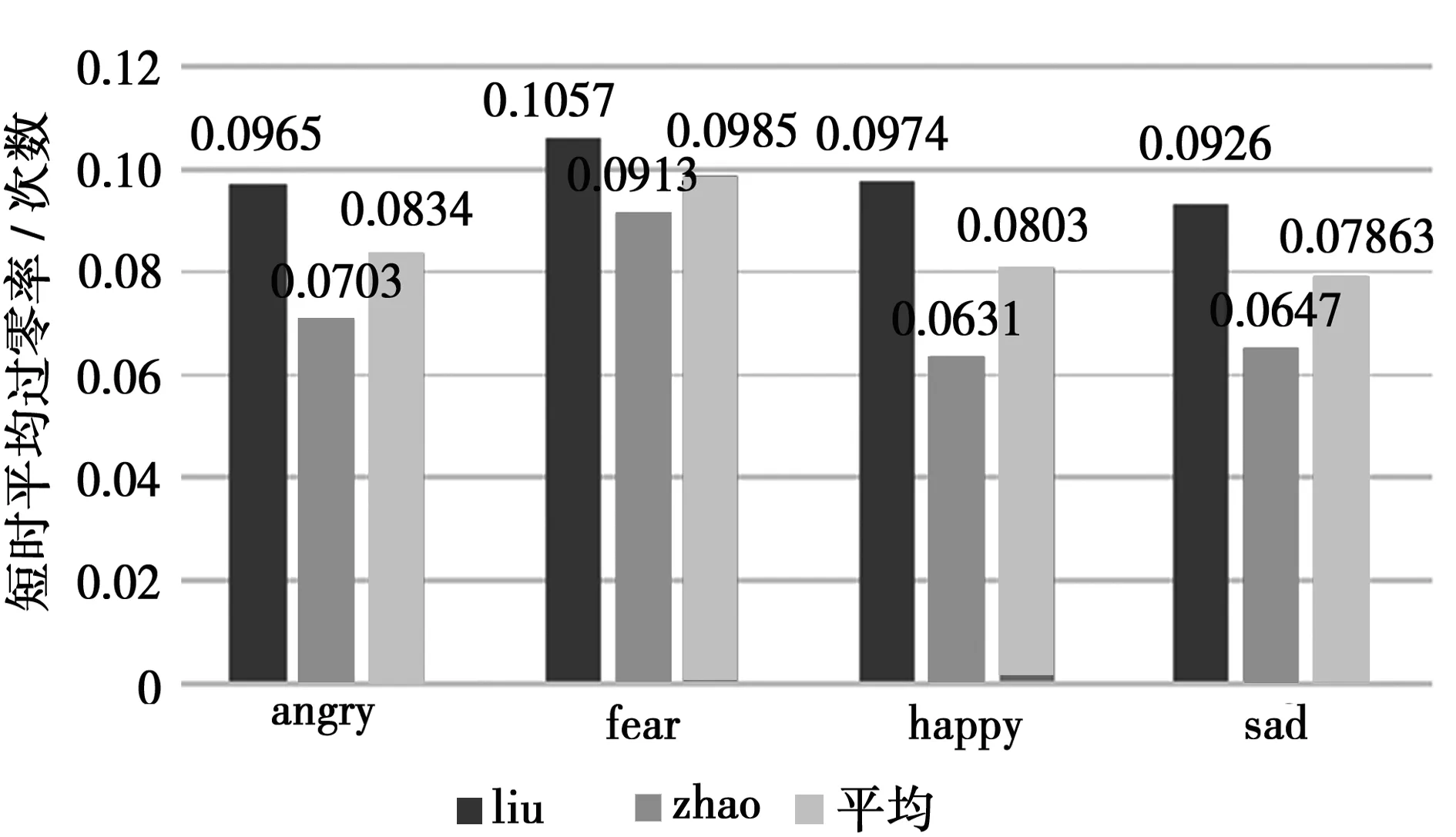
圖7 短時過零率平均值統計

聲音在通過聲道時會在某一頻率上引起共振現象，該共振的頻率就是共振峰頻率。人在不同場景下精神的緊張度有明顯不同，會影響不同情緒的產生與表達，聲道的形狀也會發生改變，共振峰的頻率值就會受到波及。

目前，共振峰的分析檢測方法主要有線性預測法、帶通濾波器組法和倒譜法等。本文選取倒譜法提取共振峰，原理是先對語音信號求快速傅里葉變換(FFT)，然后采用同態解卷技術，這樣在倒譜域中就可以簡單區分基音和聲道的相關特性，最后提取頻率最大值就可以完成參數提取。

圖8中的共振峰頻率包含多個峰值，由于各語音信號的內容不同，本文只提取第一共振峰縱向對比分析。分析結果如圖9，可看出，angry情緒下的共振峰第一個頻率峰值最大，fear情緒下較大，sad情緒下較小，happy最小；在對其共振峰頻率曲線圖分析發現，happy和angry這兩種情緒下的共振峰頻率曲線圖走向稍微上升，sad的共振峰頻率曲線圖走向則有明顯下降。這是由于人們在happy和angry情緒下容易激動并習慣性地張大嘴巴，而情緒在sad時嘴巴張開程度會小，而且還有混合著模糊的鼻音發出。

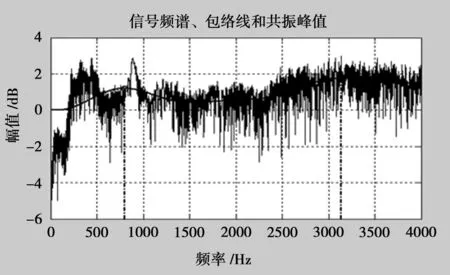
圖8 共振峰提取

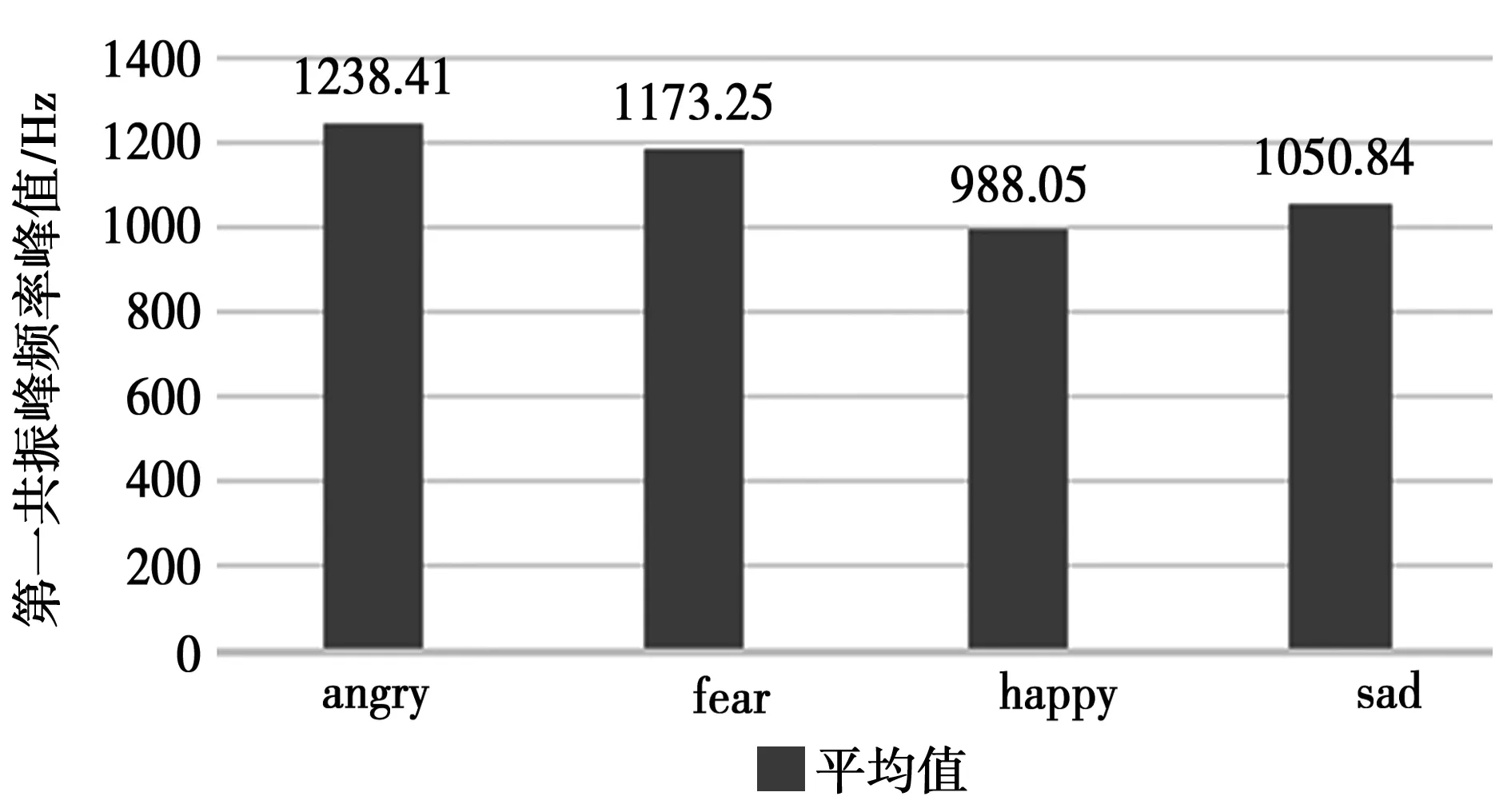
圖9 第一共振峰頻率統計

3 語音情感識別

目前仍無法準確地確定各類情感的本質特征由哪些語音情感特征參數決定，理論上說，提取統計的特征參數越詳細，情感類型越容易辨識，但實際上必須在大量情感信息中挑選出能準確反映情緒狀況的特征參數，才能獲得良好的語音情感識別性。目前已有學者分別采用主分量分析(PCA)、模糊熵理論和序列向前法等方法,對情感特征參數進行特征選擇，這些方法能顯著提高情感類型識別成功率，并且能夠降低計算的復雜程度。本文是基于PCA的特征降維對所提取的8維語音情感特征參數進行特征選擇處理。

PCA的特征選擇算法可概述為：首先對采集提取的初始特征參數進行數據歸類并組成一個初始特征參數矩陣，然后利用PCA對該矩陣進行處理，變換處理后得到特征矩陣，分析矩陣中的每個特征參數在變換時所占的權重，最后按照升序或降序對這些原始特征進行排列，并按照排序結果確定特征選擇的特征參數子集[19-21]。

PCA方法進行降低維度處理得到的特征子集與初始的特征參數集合無法存于同一維度中，但運用變換矩陣去尋找二者之間的關聯，就可以向前推測并判斷出初始特征集合內各個特征元素的變換權重，參考權重挑選出數值較大的參數。

進行語音情感特征參數選擇抽取時，對已有的n個m維的初始特征參數，先將它們化為形如x1，x2，…，xn的特征向量，然后再構建一個m行n列的矩陣去錄入數據，則Xm×n=[x1，x2，…，xn]，那么PCA的操作步驟如下所示：

(1)計算特征向量x1，x2，…，xn的均值μ和協方差矩陣COVm×n。

(2)計算出協方差矩陣COVm×n的特征值和特征向量，每個元素的特征向量與特征值按照一一對應的關系組成一個坐標形式 (λi，еi)的向量組合，依據特征值的大小可以排序為：(λ1，е1)，(λ2，е2)，…，(λm，еm)，其中λ1≥λ2≥…≥λm≥0。

(3)選取前k(k

將原始8維空間的特征參數數據向下投影到低維的空間中，具體數學公式實現如下：

PCA(x)=AT(x-μ)

(8)

根據所提取的主成分特征值與包括協方差矩陣所有特征值總和的百分比來確定未處理的高維特征向量降維。由于本文提取的8類特征參數的初始單位都不同，所以需要利用標準分數法對原始數據進行歸一化，將它們化為標準正態分布參數。

一般來說，利用PCA識別的數據，先確定其樣本信號N和提取的特征參數個數K，然后求這個K特征參數所對應的協方差矩陣，再對求得的協方差矩陣進行特征值分解，提取出K個特征值和特征向量。對于不同的情感，利用語料庫中的原始語料，分別計算出經過特征降維提取的主分量K相對于不同情感類型j所具有的均值μjk和方差σjk，并進行如下的最大可分性處理：

(9)

(10)

(11)

上式中，J為采用的語料庫情感類別個數，Lk表示第k個主分量在情感類別中的分離性，Mk表示第k個主分量在情感類別中的集中性；Hk則是用來反映主分量在情感類別中的辨別能力，Hk越大時，所提取主分量對情感類型的辨別能力越強。

識別語音情感類型時，先對K個主分量進行順序排列，然后選取p個Hk較大的主分量作為識別用的主元。經過標準分數法歸一化處理后的特征參數矢量Xstd，再利用Xstd對各個主分量的基向量Ak分別進行投影求和，獲得各個有效主分量的得分值Sk。最后利用下式計算各個主分量的綜合概率PJ，選取最大概率的情感類型作為識別情感類型。

(12)

本文利用PCA法對angry、fear、happy和sad四類情感識別，結果為0.931 4、0.896 5、0.901 6和0.867 7。在對給定語言信號情感識別中，采用本文的方法，計算正確識別率的平均值，識別率達到89.93%。

4 結 論

本文基于時間構造、基音周期和振幅能量等特征參數，提取語音情感信號中的發音持續的時間、單位時間音節發出速度、基音周期的最大值和平均值、短時過零率、語音信號第一個共振峰的最大頻率和短時能量的平均值和最大值等8個特征參數，運用PCA對提取的特征按照高興、悲傷、發怒和害怕四個類別進行分類識別，達到理想的識別效果，驗證了算法的有效性。