非平行板電容器測量楊氏模量的改進

唐子彥，冷文秀

(中國石油大學(北京) a.地球物理與信息工程學院；b.理學院，北京 102249)

楊氏模量是描述固體材料抵抗形變能力的物理量，有著重要的意義. 在大學物理實驗課中有靜力拉伸法測量楊氏模量的實驗. 使用非平行板電容器測量楊氏模量的方法大致分為2種：傳統式結構[1]和差動式結構[2]. 但這2種方法因裝置結構的限制，在可操作性、系統誤差、靈敏度上都有改進的空間. 本文提出的中心軸差動式結構,對上述問題進行改進.

1 基本原理

1.1 理論計算

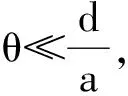
C2=C2′,

(1)

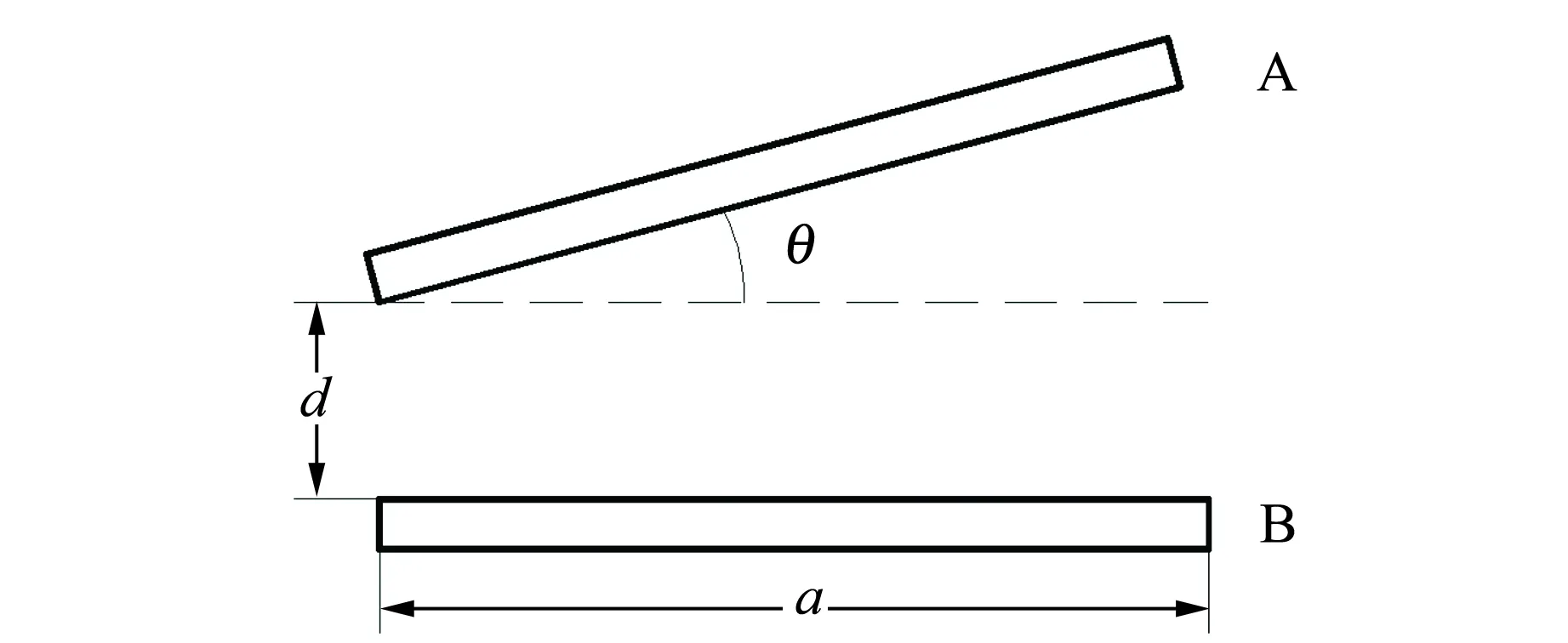
圖1 非平行板電容器

所以偏轉前的電容器的總電容為

C總′=C1′+C2′,

(2)

偏轉后的電容器的總電容為

C總=C1+C2.

(3)

由文獻[6]知,在忽略邊緣效應的情況下電容器的電容為

(4)

將(4)式作泰勒展開得：

(5)

當θ足夠小時，sinθ≈θ，故(5)可近似變為

(6)

令

則

C1=α0+α1θ+α2θ2+α3θ3+α4θ4+…

(7)

由(3)式可知偏轉后的電容器總電容為

C總=C2+α0+α1θ+α2θ2+α3θ3+α4θ4+…

(8)

由(2)式可知偏轉前(θ=0)的電容器的值為

C總′=C2′+α0,

(9)

式(8)與式(9)做差，由(1)式得

|ΔC|=|C總-C總′|=α1θ+α2θ2+α3θ3+α4θ4+…

(10)

若略去θ的二次項及以上的高次小項，得

|ΔC|=|α1θ|,

(11)

將α1代入式(11)，得

(12)

結果與文獻[1-2]中電容改變量完全一致.

最后利用電橋法測出偏轉前后電容器的改變量|ΔC|，由(12)式求出θ，通過測量鋼絲的直徑，計算出橫截面積S，鋼絲原長L，電容器轉動軸到鋼絲的距離D,再由楊氏模量的定義式及文獻[1]可以求出楊氏模量為

(13)

1.2 中心軸差動式結構電容的分析

如圖2所示，該結構的電容器由3部分組成. 圖2中上、中、下的白色部分為長寬為a的矩形金屬板，而圖中的陰影部分為剛性強度較大的絕緣材料，其長度相對于a可忽略不計，即遠小于a. 將上中下3個極板間的電容分別視作C11，C12，C21，C22，若只考慮常數項和一次項，由(7)式得：

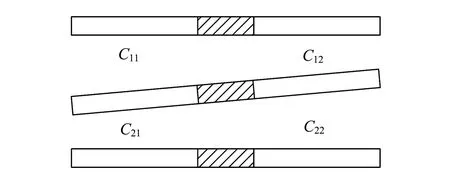
圖2 中心軸差動式結構電容器

C11=C22=α0+α1θ,

(14)

C12=C21=α0-α1θ.

(15)

令ΔCⅠ=ΔC11+ΔC22，ΔCⅡ=ΔC12+ΔC21，則由式(11)得：

ΔCⅠ=2|α1||θ|,

(16)

ΔCⅡ=-2|α1||θ|.

(17)

式(16)與式(17)相減得：

|ΔCⅠ-ΔCⅡ|=4|α1|θ.

(18)

使用電橋法測量出式|ΔCⅠ-ΔCⅡ|，即可計算出θ，再將θ代入式(13)可算出楊氏彈性模量E.

2 改進后的實驗裝置及其可操作性

2.1 實驗裝置簡介

如圖3所示，改進的主要方案是將文獻[2]裝置位于中間極板邊緣的轉動軸移至中心軸處，以組成中心軸差動式結構.

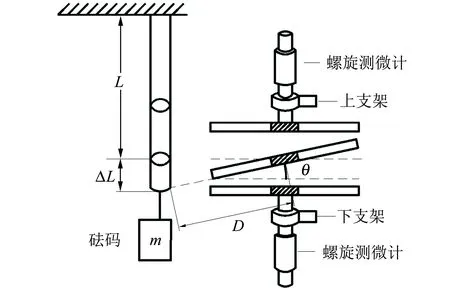
圖3 實驗裝置圖

本文所提出的的測量方案與文獻[2]類似：先使用長寬均為2a的矩形金屬板作為該電容器的上、中、下極板，并將螺旋測微計的測微螺桿的端面與電容器上下極板連接，然后將上下極板固定在絕緣支架上；中間極板的陰影部分與同為剛性強度較大的絕緣材料制成的轉動軸相連，并使轉動軸的位置固定.

實驗時，為使鋼絲保持拉直，首先在鋼絲下的砝碼盤上放上砝碼，然后把鋼絲與中極板靠近鋼絲的一端用絕緣剛性材料連接，松開固定上、下兩極板的固定旋鈕，使該電容器的3個極板完全重合后再通過調節螺旋測微計使極板間距變為d且保持中間極板平行，通過電橋測出電容，從而得出電容的改變量.

2.2 可操作性

2.2.1 可操作性及系統誤差

原有的2個實驗裝置在理論上都提出了測量楊氏模量的裝置，但是由于裝置結構的限制在可操作性上都存在問題，如在將鋼絲與轉動極板相連前，由于極板的轉軸位于其末端，極板會因為自身重量和轉軸摩擦不能平衡而發生一定程度的偏轉，會影響鋼絲發生形變時的伸長長度，或者理解為極板發生轉動的角并不完全因為鋼絲形變而產生，一部分轉動是由于極板自身重量而產生. 針對上述2種裝置可操作性存在的問題，本文提出的裝置結構將轉軸的位置放置于極板中間使得極板可通過自身重量保持平衡在實驗開始前并不發生轉動，讓角的改變盡可能通過鋼絲形變產生，使實驗的可操作性提高的同時大大降低系統誤差.

2.2.2 另一種實驗方式

當被測物體為柱狀時可以使用圖4所示的實驗裝置進行測量，電容器部分的結構與圖3一致，因被測物為柱狀物體，所以可以用已知質量的重物或者已知大小的壓力作用在物體的頂端，即可更準確、誤差更小地測量出楊氏彈性模量.

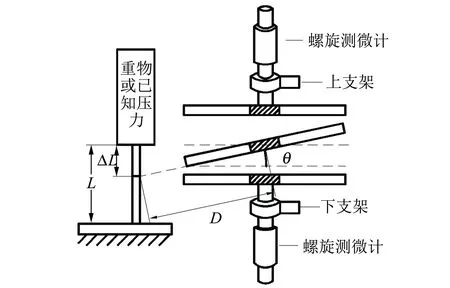
圖4 實驗裝置圖

3 靈敏度、誤差分析及測試結果

3.1 電容器的靈敏度

用電容的響應量(即電容的改變量)ΔC和初始時的電容C0之比來表示靈敏度[7]，記作s，不考慮邊緣效應和分布電容的影響，可得

(19)

如圖1所示，文獻[1]中電容器的改變量ΔC1為

ΔC1=α1θ,

(20)

由式(19)及式(20)得文獻[1]中裝置靈敏度s1為

(21)

由文獻[2]知：

ΔC2=2α1θ,

(22)

所以文獻[2]中實驗裝置的靈敏度s2為

(23)

中心軸差動式結構的靈敏度記作s3，由式(18)知：

ΔC3=|ΔC1-ΔCΠ|=4|α1|θ,

(24)

由此得

(25)

通過對比式(23)及式(25)可得

s3=2s2=4s1.

(26)

可以得出結論：在電容器的靈敏度方面，本文中的中心軸差動式結構有了很大的提高，分別是文獻[1]和文獻[2]裝置靈敏度的2倍和4倍.

3.2 相對非線性誤差

文獻[2]中已詳細給出相對非線性誤差的計算過程，中心軸差動式結構在相對非線性誤差上與文獻[2]相同，也就證明了相對非線性誤差遠小于文獻[1]，使相對非線性誤差大大降低.

3.3 測試結果

利用本裝置測得的鋼絲的楊氏彈性模量E=(1.98±0.43)×1011N/m2. 由實驗結果可以得出：在理論和實踐中，使用本裝置進行楊氏彈性模量的測定都符合實際要求.

4 結束語

基于非平行板電容器的楊氏模量測量裝置，采用中心軸差動式結構. 轉軸設置于中極板的中心處，邊緣效應和測量系統的分布電容對實驗的影響被基本消除，在中極板與鋼絲連接之前，中極板可通過自身重力保持平衡，以免在實驗開始之前中極板發生偏轉，使實驗過程中得到的中極板的轉動角度更加精確. 測試結果表明本裝置能有效地提高電容器測法測量楊氏彈性模量的精確度和靈敏度，降低系統誤差.