超大柔性空間結(jié)構(gòu)姿態(tài)振動(dòng)耦合穩(wěn)定性分析

穆瑞楠，譚述君,2，吳志剛,2，齊朝暉

(1. 大連理工大學(xué)工業(yè)裝備結(jié)構(gòu)分析國(guó)家重點(diǎn)實(shí)驗(yàn)室，大連 116024；2. 大連理工大學(xué)航空航天學(xué)院，大連 116024)

0 引 言

以空間太陽(yáng)能電站為代表，各類超大柔性空間結(jié)構(gòu)概念相繼出現(xiàn)[1-2]。這種結(jié)構(gòu)的尺寸通常要達(dá)到千米量級(jí)，遠(yuǎn)超人類現(xiàn)有最大的空間結(jié)構(gòu)——百米量級(jí)的國(guó)際空間站。隨著結(jié)構(gòu)尺寸的大幅增加，空間結(jié)構(gòu)具有高柔性、質(zhì)量分布高分散性、高面質(zhì)比等特性。在環(huán)境干擾作用下，姿態(tài)運(yùn)動(dòng)和結(jié)構(gòu)振動(dòng)之間的耦合效應(yīng)增強(qiáng)，有可能引發(fā)不穩(wěn)定現(xiàn)象。因此，需要分析姿態(tài)運(yùn)動(dòng)與結(jié)構(gòu)振動(dòng)之間的耦合作用，以及系統(tǒng)參數(shù)對(duì)穩(wěn)定性的影響。

在這一方面，已有學(xué)者以不同的簡(jiǎn)化模型開展了相關(guān)研究。以超大空間啞鈴模型為簡(jiǎn)化研究對(duì)象，Sanyal等[3]推導(dǎo)了平衡位置處的線性化模型，分析了在兩種平衡狀態(tài)下的穩(wěn)定性。穆瑞楠等[4]通過(guò)仿真分析，發(fā)現(xiàn)了結(jié)構(gòu)振動(dòng)引起的姿態(tài)運(yùn)動(dòng)不穩(wěn)定現(xiàn)象。此外，以超大空間桿梁連續(xù)體模型為簡(jiǎn)化研究對(duì)象，Ashley[5]分析了不同姿態(tài)運(yùn)動(dòng)條件下的彈性桿結(jié)構(gòu)振動(dòng)穩(wěn)定性問(wèn)題，指出姿態(tài)運(yùn)動(dòng)對(duì)結(jié)構(gòu)振動(dòng)穩(wěn)定性具有影響。Silva[6]給出考慮環(huán)境干擾的柔性梁平衡位置處非線性擾動(dòng)方程，并用擾動(dòng)分析方法討論了系統(tǒng)可能出現(xiàn)的共振現(xiàn)象。Liu[7]考慮動(dòng)力剛化效應(yīng)，提出參數(shù)激勵(lì)模型(PEM)，可更精確地描述在自旋姿態(tài)運(yùn)動(dòng)時(shí)的結(jié)構(gòu)振動(dòng)。Kumar 等[8]在小初始姿態(tài)角條件下，建立了3階Hill方程形式的柔性梁振動(dòng)方程，并發(fā)現(xiàn)對(duì)于模態(tài)頻率與軌道角速率之比的平方較低時(shí)引起的不穩(wěn)定現(xiàn)象。Shrivastava等[9]在Kumar等人的工作基礎(chǔ)上，引入結(jié)構(gòu)阻尼，并利用攝動(dòng)方法考慮結(jié)構(gòu)阻尼對(duì)結(jié)構(gòu)振動(dòng)穩(wěn)定性的影響。魏乙等[10]在約束Hamilton體系下建立了繩系構(gòu)型的軌道、姿態(tài)和結(jié)構(gòu)振動(dòng)的耦合模型，發(fā)現(xiàn)平臺(tái)總體質(zhì)量變化對(duì)其振動(dòng)周期具有影響。Ishimura等[11]基于同一構(gòu)型，分析了質(zhì)量比、頻率比以及長(zhǎng)度比對(duì)系統(tǒng)穩(wěn)定性的影響，仿真結(jié)果表明頻率比影響最大，在某些參數(shù)范圍內(nèi)質(zhì)量比影響較大。同時(shí)，Ishimura等[12]從勢(shì)能角度提出評(píng)估系統(tǒng)穩(wěn)定性的新方法，給出太陽(yáng)能陣列平臺(tái)在平衡位置附近的結(jié)構(gòu)振動(dòng)穩(wěn)定性。McNally 等[13]基于算盤構(gòu)型，分析了超大柔性空間結(jié)構(gòu)在拉普拉斯軌道下的耦合動(dòng)力學(xué)特性。Zhang等[14]建立了空間熱輻射與結(jié)構(gòu)振動(dòng)的耦合模型，分析了在熱輻射作用下的結(jié)構(gòu)振動(dòng)穩(wěn)定性。Gettliffe[15]分析了帶有電磁機(jī)構(gòu)的繩系空間結(jié)構(gòu)的運(yùn)動(dòng)穩(wěn)定性。

本文在前期工作[4,16]的基礎(chǔ)上，建立柔性梁在圓軌道下的姿態(tài)運(yùn)動(dòng)與彎曲振動(dòng)的耦合動(dòng)力學(xué)模型，分析姿態(tài)運(yùn)動(dòng)與重力梯度對(duì)模態(tài)頻率的影響，并將柔性振動(dòng)模態(tài)方程化為Mathieu方程形式，分析姿態(tài)運(yùn)動(dòng)幅度對(duì)柔性振動(dòng)穩(wěn)定性的影響。

1 在軌柔性梁的動(dòng)力學(xué)建模

考慮細(xì)長(zhǎng)的Euler-Bernoulli梁，建立超大柔性空間結(jié)構(gòu)的動(dòng)力學(xué)模型。假設(shè)空間結(jié)構(gòu)在圓軌道運(yùn)行，其姿態(tài)運(yùn)動(dòng)和彎曲變形均在軌道平面內(nèi)，如圖1所示，其中Oe表示地心，Re表示地球半徑，rc表示空間結(jié)構(gòu)質(zhì)心處所在的軌道半徑。

慣性坐標(biāo)系和軌道坐標(biāo)系分別用Oexeye和Ooxoyo表示，其坐標(biāo)原點(diǎn)均位于地心。而浮動(dòng)坐標(biāo)系用Cxy表示，其坐標(biāo)原點(diǎn)位于柔性梁的質(zhì)心。梁上任一點(diǎn)P的坐標(biāo)向量和變形向量分別用ρP和wP表示。基于質(zhì)心浮動(dòng)坐標(biāo)系的定義，這兩個(gè)向量滿足以下三個(gè)條件：

(1)

(2)

(3)

rp=Teorc+TeoToa(ρP+wP)

(4)

其中Teo和Toa分別表示從軌道坐標(biāo)系到慣性坐標(biāo)系和從浮動(dòng)坐標(biāo)系到軌道坐標(biāo)系的坐標(biāo)轉(zhuǎn)換矩陣。由此得到柔性梁的動(dòng)能為

(5)

(6)

其中ms表示結(jié)構(gòu)的總質(zhì)量，I表示結(jié)構(gòu)的轉(zhuǎn)動(dòng)慣量，其表達(dá)式為

柔性梁的重力勢(shì)能可表示為

(7)

引入空間結(jié)構(gòu)尺寸與軌道半徑的尺寸比，重力勢(shì)能的分母可展開成泰勒級(jí)數(shù)的形式為

(8)

其中ic表示軌道半徑rc方向的單位向量。

基于Sincarsin[17]研究工作中的高階慣性矩的遞推定義，重力勢(shì)能可近似表示為

(9)

其中特殊算子?表示并乘算子。將第一個(gè)簡(jiǎn)化條件式(1)代入式(9)，則重力勢(shì)能可簡(jiǎn)化為

(10)

柔性梁的彈性勢(shì)能可表示為

(11)

其中D材料的剛度系數(shù)矩陣，εE表示彈性應(yīng)變。

對(duì)于在軌道平面內(nèi)運(yùn)動(dòng)的柔性梁結(jié)構(gòu)，可定義相應(yīng)的向量和坐標(biāo)轉(zhuǎn)換矩陣。其中，在軌道坐標(biāo)系內(nèi)定義的軌道半徑向量rc和軌道運(yùn)動(dòng)的角速度ωeo為

其中θ表示平面軌道角，而ωo表示軌道角速度。在浮動(dòng)坐標(biāo)系內(nèi)定義的位置向量ρP、彎曲變形向量wP以及姿態(tài)運(yùn)動(dòng)的角速度ωoa分別為

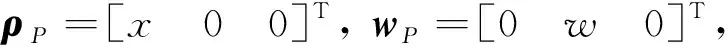
其中x表示柔性梁的軸向坐標(biāo)，w表示柔性梁的橫向變形，而φ表示平面姿態(tài)角。坐標(biāo)轉(zhuǎn)換矩陣為

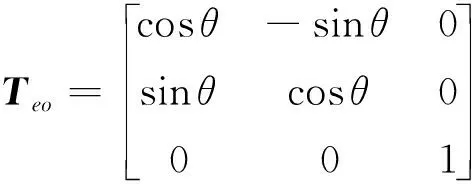
引入模態(tài)疊加法，彎曲變形可表示為

w(x,t)=φT(x)q(t)

(12)

其中φ(x)自由振動(dòng)的彎曲模態(tài)函數(shù)列陣，q(t)表示模態(tài)坐標(biāo)列陣。

以姿態(tài)角φ和模態(tài)坐標(biāo)q(t)為廣義坐標(biāo)。利用Hamilton原理建立姿態(tài)運(yùn)動(dòng)和彎曲變形的耦合動(dòng)力學(xué)模型，其中重力梯度項(xiàng)保留至尺寸比的二次項(xiàng)(參考式)。

qTR2q(15sin2φ-11)sinφ)=0

(13)

2R2q(5cos2φ-4)cosφ)=0

(14)

其中總質(zhì)量ms、轉(zhuǎn)動(dòng)慣量I、模態(tài)質(zhì)量矩陣Mq、模態(tài)剛度矩陣K、以及模態(tài)函數(shù)的積分列陣和矩陣可表示為

2 結(jié)構(gòu)振動(dòng)頻率影響分析

通過(guò)簡(jiǎn)化結(jié)構(gòu)振動(dòng)方程式，彎曲振動(dòng)的第一階頻率可以表示為

(15)

其中ωs表示結(jié)構(gòu)彎曲振動(dòng)基頻。從式可以看出，結(jié)構(gòu)振動(dòng)頻率受到系統(tǒng)轉(zhuǎn)動(dòng)和重力梯度兩方面影響，等式右端第二項(xiàng)為轉(zhuǎn)動(dòng)耦合項(xiàng)，等式右端第三項(xiàng)為重力梯度項(xiàng)。在無(wú)主動(dòng)控制的重力梯度穩(wěn)定情況下，系統(tǒng)的姿態(tài)運(yùn)動(dòng)接近于簡(jiǎn)諧運(yùn)動(dòng)，由式可以看出，結(jié)構(gòu)振動(dòng)的頻率會(huì)隨姿態(tài)變化而波動(dòng)。

將姿態(tài)運(yùn)動(dòng)近似表示為φ=φ0cosτ，其中φ0為初始姿態(tài)角，τ=kωot定義為廣義時(shí)間，其中kωo為姿態(tài)運(yùn)動(dòng)頻率。k與φ0的取值相關(guān)，通過(guò)近似的姿態(tài)運(yùn)動(dòng)響應(yīng)與由耦合模型仿真得到的姿態(tài)運(yùn)動(dòng)響應(yīng)相擬合，得到不同初始姿態(tài)角下的k取值，如圖2(a)所示，而其擬合精度如圖2(b)所示。由圖可見(jiàn)在[ 0, 0.4π rad )范圍內(nèi)，擬合精度小于5%，因此這種近似是合理的。

(16)

圖3給出式(16)中的轉(zhuǎn)動(dòng)耦合項(xiàng)和重力梯度項(xiàng)對(duì)結(jié)構(gòu)振動(dòng)頻率隨時(shí)間變化的影響曲線。對(duì)于小幅姿態(tài)運(yùn)動(dòng)情況(φ0= 0.1 rad)，對(duì)應(yīng)的k=1.726，圖3(a)中可見(jiàn)，在姿態(tài)運(yùn)動(dòng)幅度較小時(shí)，重力梯度作用使結(jié)構(gòu)振動(dòng)頻率增加近似一倍軌道頻率，但轉(zhuǎn)動(dòng)耦合項(xiàng)使結(jié)構(gòu)振動(dòng)頻率降低約一倍軌道頻率，二者影響近似相互抵消，此時(shí)結(jié)構(gòu)振動(dòng)頻率變化幅度較小。對(duì)于大幅姿態(tài)運(yùn)動(dòng)(φ0= π/4 rad)，對(duì)應(yīng)的k=1.469，從圖3(b)可以看出，重力梯度項(xiàng)波動(dòng)幅度增大至一倍軌道頻率，時(shí)而使結(jié)構(gòu)振動(dòng)頻率增大，時(shí)而使其減小。轉(zhuǎn)動(dòng)耦合項(xiàng)仍使結(jié)構(gòu)振動(dòng)頻率降低，其量級(jí)增大至兩倍軌道頻率。

3 穩(wěn)定性分析

通過(guò)對(duì)彎曲振動(dòng)模態(tài)方程式(14)的合理簡(jiǎn)化，可化為Mathieu方程形式。忽略式中重力梯度的尺寸比二次項(xiàng)，則第n階的模態(tài)方程為

(17)

不失一般性的假設(shè)姿態(tài)運(yùn)動(dòng)為φ=φ0sinτ，其中τ=kωot+π/2。同時(shí)，引入簡(jiǎn)化變量

將假設(shè)的姿態(tài)角φ的表達(dá)式代入模態(tài)方程式(17)，并用τ的微分式替換t的微分式，同時(shí)代入簡(jiǎn)化變量ε和δn，則模態(tài)方程式(17)化為

(18)

從(18)式可見(jiàn)，模態(tài)方程由此化為高階Mathieu方程，其中ε為小參數(shù)。基于穩(wěn)定性的攝動(dòng)分析方法，令模態(tài)坐標(biāo)qn和參數(shù)δn為

qn=qn 0+εqn 1+ε2qn 2

(19)

(20)

將模態(tài)坐標(biāo)qn和參數(shù)δn的表達(dá)式代入Mathieu方程式(18)，比較小參數(shù)ε同冪次頂系數(shù),得

(21)

(22)

(23)

由小參數(shù)ε的零次冪方程式解得

qn 0=a0cos(δn 0τ)+b0sin(δn 0τ)

(24)

其中a0和b0為待定常數(shù)，由彎曲變形的初始條件決定。由于Mathieu方程的特點(diǎn)，在式(18)的小參數(shù)一次項(xiàng)的余弦函數(shù)中，廣義時(shí)間的系數(shù)為1，因此參數(shù)δn 0=1/2及其附近為主要共振區(qū)域。將式(24)及參數(shù)δn 0代入小參數(shù)ε的一次冪方程式(22)。為了消除一次冪方程中的永年項(xiàng)，出現(xiàn)兩種情況，分別為

(25)

(26)

qn 0=a0cos(0.5τ)

將qn 0和qn 1的表達(dá)式代入小參數(shù)ε的二次冪方程，并為了消除二次冪方程中的永年項(xiàng)，可得

(27)

解得

(28)

由式(25)和式(27)可得，第一種情況下的參數(shù)δn表達(dá)式為

(29)

(30)

由式(29)和式(30)，得到不同初始姿態(tài)角下的穩(wěn)定區(qū)域如圖4所示。由圖2(a)可知，隨著初始姿態(tài)角增大，姿態(tài)運(yùn)動(dòng)頻率與軌道角速度之比k減小，而不穩(wěn)定區(qū)域增大。

4 結(jié) 論

本文以超大柔性空間柔性梁為研究對(duì)象，基于Hamilton原理建立其姿態(tài)運(yùn)動(dòng)-柔性振動(dòng)的耦合動(dòng)力學(xué)模型，分析了彎曲振動(dòng)的影響因素以及其穩(wěn)定性。得到結(jié)論如下：

1)在小初始姿態(tài)角下，重力梯度和轉(zhuǎn)動(dòng)耦合項(xiàng)相互抵消。而在大初始姿態(tài)角下，重力梯度項(xiàng)呈簡(jiǎn)諧波動(dòng)，其幅度約一倍軌道頻率。轉(zhuǎn)動(dòng)耦合項(xiàng)使結(jié)構(gòu)振動(dòng)頻率降低約兩倍軌道頻率。

2)初始姿態(tài)角影響結(jié)構(gòu)振動(dòng)的穩(wěn)定區(qū)域，隨著初始姿態(tài)角的增大，姿態(tài)運(yùn)動(dòng)頻率降低，結(jié)構(gòu)振動(dòng)的不穩(wěn)定區(qū)域增大。