雙體衛星對日定向姿態機動控制

耿遠卓，李傳江，孫延超，馬廣富

(哈爾濱工業大學控制科學與工程系，哈爾濱 150001)

0 引 言

隨著空間觀測任務的多樣化和復雜化以及空間觀測技術的不斷發展，對日觀測作為空間科學的重要任務之一受到廣泛關注。高精度對日觀測是提升人類對太陽認知的基礎，其實質就是高精度對日定向控制問題。但是由于傳統衛星平臺與載荷存在物理連接，衛星平臺上安裝的飛輪和陀螺轉子高速旋轉時產生的高頻微振動以及太陽帆板的撓性振動通過衛星平臺傳遞給載荷，嚴重影響載荷的觀測精度和穩定度[1]。

為了從根本上提高衛星載荷控制精度，美國Lockheed公司于2002年首次提出“ Disturbance Free Payload (DFP)”衛星的概念，通過將載荷和平臺物理隔離，形成載荷艙和平臺艙的雙體結構，實現了真正意義的振動隔離，為有效提升載荷的控制精度和穩定度奠定了物理基礎[2]。文獻[3-8]對DFP系統進行了更加深入的研究，通過地面模擬試驗驗證了DFP隔振性能和姿態機動能力。受DFP設計思想的啟發，文獻[9-10]提出了雙體衛星的概念，并建立了雙體衛星運動模型，設計了基于PD控制的姿態穩定控制策略。文獻[11]借鑒DFP設計思想，提出了一種六自由度微振動模擬器，推導了其逆動力學模型并設計了PI控制律。文獻[12]建立了DFP衛星磁浮機構對兩艙作用力和力矩模型，基于PD控制實現了兩艙姿態及相對位置控制。文獻[1]通過Kane法對六桿球面Stewart平臺進行了動力學建模，并通過六個執行器產生控制力進行振動抑制控制，并且考慮了結構參數(阻尼比、剛度系數、質心位置)不確定性。文獻[13]提出了非接觸Stewart衛星模型。將衛星載荷部分和平臺部分用六桿磁浮機構分開，采用Newton-Euler法對衛星整體進行建模，利用混合靈敏度控制方法實現了高精度姿態指向控制。文獻[14]建立了DFP衛星兩艙之間柔性電纜的動力學模型，分析了柔性電纜對兩艙控制精度和隔振性能的影響。但是上述文獻僅是針對DFP衛星的姿態穩定控制及相應動力學分析，對于大角度三軸姿態機動問題還沒有相關研究結果。

為了解決衛星姿態機動過程中撓性振動問題，眾多學者做了相關研究[15-18]，盡管在一定程度上抑制了撓性衛星姿態機動時的撓性振動，但由于物理結構的限制，難以從根本上實現振動隔離。

本文為實現雙體衛星高精度對日定向，首先建立對日基準坐標系。針對雙體衛星特點，建立雙體衛星平臺艙和載荷艙姿態運動模型及平動模型。利用傳統PD控制實現雙體衛星對日定向姿態機動及避碰控制。為進一步提升平臺艙對載荷艙的姿態跟蹤速度，考慮飛輪動態特性并進行補償，基于反步法提出一種改進的姿態跟蹤控制律。為提升兩艙協同控制性能，在PD 控制的基礎上，提出一種載荷艙變增益姿態控制策略，考慮了載荷艙姿態機動過程中平臺艙姿態跟蹤情況，避免了兩艙姿態機動速度不匹配而導致的碰撞問題。

1 對日基準及雙體衛星模型的建立

1.1 對日基準坐標系的建立

本文假設光學相機沿載荷艙Z軸安裝，因此需要將載荷艙Z軸指向太陽。建立對日基準坐標系如下：以地球中心為原點O，以日地連線作為基準軸Zr，以黃道面法向方向作為Yr，根據右手定則得到Xr，如圖1所示。控制載荷艙使其本體系與對日基準坐標系O-XrYrZr重合，即可完成對日定向。

1.2 雙體衛星結構及工作機理

雙體衛星結構示意圖如圖2所示。載荷艙主要安裝望遠鏡、雷達等有效載荷，太陽帆板、飛輪等振動源全部安裝在平臺艙。與傳統衛星不同，平臺與載荷不固連，兩者通過八個正交安裝的磁浮機構連接在一起。磁浮機構可提供磁力，是載荷艙姿態及兩艙相對位置控制的執行機構。衛星需要姿態機動時，磁浮機構產生力作用在載荷艙上，合成姿態控制力矩，驅動載荷艙轉動。同時，平臺艙以載荷艙姿態信息為期望姿態指令進行姿態跟蹤。在兩艙姿態機動過程中，磁浮機構的磁鋼和線圈會產生相對運動，因此需要進行相對位置控制以避免碰撞。

1.3 姿態運動模型

根據兩艙的工作機理，載荷艙要實現主動對日定向，由于對日基準坐標系的角速度很小，將其忽略，得到載荷艙相對對日基準坐標系的姿態誤差動力學與運動學方程如式(1)和式(2)所示。

(1)

(2)

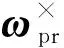
平臺艙為從動控制，其控制目標為跟蹤載荷艙姿態。假設平臺艙撓性帆板較小，因此忽略撓性影響。平臺艙相對載荷艙姿態誤差方程如下

(3)

(4)

1.4 磁浮機構線圈與磁鋼的相對位置模型

由于兩艙不固連，在姿態機動過程中很可能發生碰撞，即安裝在載荷艙上的磁鋼與平臺艙上的線圈會發生碰撞。所以，首先需要推導出線圈與磁鋼的相對位置表達式，為兩艙的避碰控制奠定基礎。

如圖3所示，雙體衛星的磁浮機構成對且對稱安裝，其中B1,B3可提供沿載荷艙Y軸的力，B2,B4可提供沿載荷艙X軸的力，A1,A2,A3,A4可提供沿載荷艙Z軸的力。圖4是單個磁浮機構放大圖，左側為線圈，右側為磁鋼，磁鋼中為勻強磁場，圖中a,b分別表示線圈端點與磁鋼中心點。

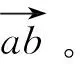
rab=rsb-rsa=rsp+rpb-rsa

(5)

式中：rsp表示兩艙質心相對位置向量，rpb表示載荷艙質心指向磁鋼中心點向量，rsa表示平臺艙質心指向線圈端點向量。為了分析方便，將各向量表示在載荷艙本體系中，可得

(6)

Rps=AZ(ψps)AY(θps)AX(φps)

(7)

式中：

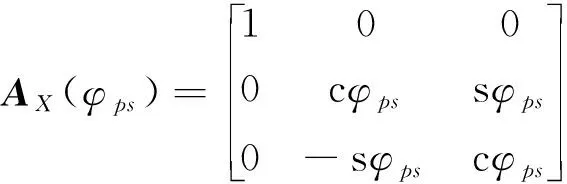
式中：c和s代表cos和sin。φps,θps和ψps分別表示載荷艙相對平臺艙的滾轉角、俯仰角和偏航角。由于兩艙相對姿態角很小，因此在小角度假設下可得

(8)

對于B1磁浮機構

(9)

(10)

其余磁浮機構線圈與磁鋼相對位置的分析與B1相同，因此不再贅述。各磁浮機構線圈與磁鋼軸向相對位置表達式如式(11)所示。

(11)

2 雙體衛星對日定向控制律設計

2.1 基于PD控制的對日定向控制律設計

鑒于PD控制具有可靠性高、易于工程實現、魯棒性強、物理意義明確等優點，本節首先設計PD控制律實現載荷艙主動姿態機動及平臺艙姿態跟蹤。設計兩艙姿態控制律如式(12)和式(13)所示。

Tp=-kppJpqpr-kpdJpωpr

(12)

(13)

式中：kpp,kpd為載荷艙PD控制參數，ksp,ksd為平臺艙PD控制參數。

采用式(12)傳統PD控制律雖然可實現載荷艙主動姿態機動控制，但是當初始姿態偏差較大時，控制力矩較大，載荷艙角加速度較大，平臺艙難以跟蹤，兩艙易發生碰撞。將式(12)控制律進行改進，得到式(14)切換形式的控制律。

Tp_i=

(14)

式中：Tp_i為載荷艙第i(i=1,2,3)軸的控制力矩，Ji為對應的轉動慣量對角線元素，ωpr_i和qpr_i分別表示載荷艙相對對日基準坐標系的誤差角速度和誤差四元數向量部分對應分量，ε為正常數，決定了載荷艙姿態機動速度。sgn表示符號函數。

當qpr_i減小至ε時，切換為PD控制模式。系統穩態性能指標不受ε影響，可以通過增大kpp來降低穩態誤差，通過減小ε保證姿態機動平穩。ε的取值應大于姿態穩態精度，以避免控制頻繁切換。

2.2 考慮飛輪動態特性的平臺艙姿態跟蹤控制律設計

在第2.1節中，針對平臺艙姿態跟蹤問題，設計了PD控制律，較好地實現了平臺艙跟隨載荷艙轉動的目標。但是平臺艙姿態控制的執行機構一般為飛輪，由于飛輪動態特性的影響，其帶寬遠低于磁浮機構，影響了平臺艙姿態跟蹤效果。本節將對飛輪動態特性進行補償處理，基于反步法設計姿態控制律，提升平臺艙姿態跟蹤速度。

考慮飛輪模型為簡化的一階慣性環節，其動態方程為[19]

(15)

式中：tws為飛輪慣性常數。uo，uin分別為飛輪輸出力矩與輸入指令。利用反步法設計控制律如下。

步驟1: 取Lyapunov函數V1=k(1-qsp 0)，對其求導

(16)

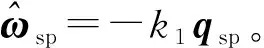
(17)

令uo為虛擬變量，其期望值取為

(18)

(19)

設計飛輪輸入指令uin如下，

(20)

定理1. 針對式(3)平臺艙姿態跟蹤動力學，考慮式(15)飛輪動態特性，設計反步控制律，可實現平臺艙對載荷艙姿態的全局漸近跟蹤控制。

證. 定理1的證明可由前文步驟1, 步驟2和步驟3的推導得到，這里不再贅述。

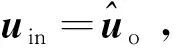
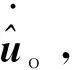
2.3 基于變增益PD控制的載荷艙對日定向控制律設計

第2.1節中載荷艙主動對日定向控制過程沒有考慮平臺艙姿態跟蹤效果，為了避免兩艙碰撞，必須減小載荷艙控制器參數，犧牲載荷艙姿態機動速度。否則在任務起始時刻平臺艙姿態難以快速跟蹤。但是姿態機動起始和結束階段持續時間非常短，姿態機動的大部分過程兩艙相對位移和相對姿態很小，較小的載荷艙姿態機動控制參數降低了整個任務過程的姿態機動速度，保守性較強。

因此，本節將對式(12)載荷艙姿態機動控制律進行改進，考慮平臺艙姿態跟蹤誤差，設計變增益對日定向姿態機動控制律，提高兩艙協同控制性能。

設計載荷艙變增益姿態控制律如式(21)所示，

(21)

式中：qsp和qsp0為平臺艙相對載荷艙的姿態誤差四元數向量和標量部分。δ為一很小的正常值，目的是避免當qsp為0時，控制律發生奇異。

定理2. 針對式(1)和式(2)載荷艙姿態模型，在變增益控制律(21)的作用下，當不考慮環境干擾力矩時，載荷艙姿態控制閉環系統是漸近穩定的。

證. 選取Lyapunov函數如下

(22)

將其對時間求導得

(23)

將控制律(21)代入(23)可得

(24)

由LaSalle不變集原理可得

limt→∞ωpr=0, limt→∞qpr=0。

即實現了姿態機動控制任務。

注3. 對于控制律(21)，由于兩艙相對姿態很小，因此ωsp和qsp均為小量，式(21)可以近似表示為

(25)

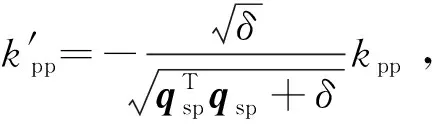
注4. 為保證姿態控制過程過渡平穩，載荷艙仍可采用類似式(14)的切換控制策略，即控制律(25)可修改為如式(26)所示。

Tp_i=

(26)

式中：qpr_i和ωpr_i(i=1,2,3)為載荷艙相對對日基準坐標系的姿態四元數向量部分的分量及角速度分量。

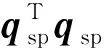
本節給出的變增益控制策略(26)在載荷艙姿態機動過程中考慮了平臺艙姿態信息，因此更好地實現兩艙協同控制。需要說明的是，平臺艙的姿態信息只出現在載荷艙控制系數中，并沒有直接在控制律中作為單獨一部分，不會將平臺艙所受擾動傳遞給載荷艙，仍然可以將微振動隔離，保證了載荷艙超高精度、超高穩定度的設計初衷。

2.4 兩艙避碰控制

通過前述兩艙姿態控制策略可實現兩艙姿態的協同，但是由于磁浮機構安裝于兩艙表面，在兩艙繞各自質心旋轉的過程中，磁浮機構的磁鋼和線圈會產生相對運動。因此，為避免磁浮機構碰撞，還需要設計兩艙相對位置控制器。

根據式(11)定義變量S=[rps_xrps_yrps_z]T,rps_x,rps_y和rps_z的定義如式(27)所示。

(27)

這里定義的S將作為兩艙相對位置控制變量。如此選擇S的形式有如下優點：1) 充分利用各傳感器測距信息，通過取平均值可以在一定程度上避免測量噪聲的影響；2) 保證了只有當兩艙繞非共質心軸旋轉時才提供相對位置控制力，否則如果兩艙繞共質心軸Z轉動，則根據式(27)可知此時S=0，無需相對位置控制，只需要平臺艙姿態跟蹤載荷艙姿態即可。

設計避碰控制律如下

(28)

式中：Fps為八個磁浮機構提供的三軸合力，kpf和kdf為控制系數。

根據圖3所示磁浮機構安裝位置和衛星結構，得到磁浮機構輸出力FB1,FA1,FB2,FA2,FB3,FA3,FB4和FA4，與三軸轉動力矩Tp_x,Tp_y,Tp_z及平動力Fps_x,Fps_y,Fps_z的關系如式(29)所示，式中矩陣A為分配矩陣。矩陣A的秩為6，保證了解的存在性。

[Fps_xFps_yFps_zTp_xTp_yTp_z]T=

A[FB1FA1FB2FA2FB3FA3FB4FA4]T

(29)

A=

為了將期望控制力和控制力矩正確分配給八個磁浮機構，使得磁浮機構輸出力可以合成期望力和力矩，需要進行控制分配方案設計。本文利用偽逆控制分配方案，即

[FB1FA1FB2FA2FB3FA3FB4FA4]T=

A+[Fps_xFps_yFps_zTp_xTp_yTp_z]T

(30)

式中:A+表示A的偽逆矩陣。

3 仿真分析

雙體衛星物理結構參數如下：

載荷艙及平臺艙轉動慣量矩陣

載荷艙及平臺艙質量mpa=100 kg,mser=160 kg。兩艙結構參數為L1=0.55 m，L2=0.55 m，L3=0.63 m。磁浮機構線圈和磁鋼相對運動范圍為(-5 mm,5 mm)。兩艙執行機構性能參數如表1所示。

表1 兩艙執行機構性能參數Table 1 Parameters of actuators for payload and platform

3.1 基于PD控制的雙體衛星對日定向控制

取式(13)、(14)和(28)控制參數如表2所示。

表2 PD控制器參數Table 2 The PD controller parameters

兩艙初始姿態均與慣性系重合，環境干擾力矩考慮小幅值(約為10-4N·m)慢變正弦信號。為了更好的展現兩艙姿態，在仿真中將姿態四元數轉換成了歐拉角進行顯示。仿真結果如下：

載荷艙在PD控制律作用下1000 s左右完成了對日定向姿態機動控制，由圖 5局部放大圖可知，在2000 s之后，載荷艙對日定向誤差姿態角達到5×10-3(°)，姿態穩定度達到5×10-7(°/s)。雙體衛星的姿態機動速度較為緩慢是由于特殊的衛星結構導致的，兩艙無物理連接，這要求平臺艙以較快速度跟蹤載荷艙姿態，載荷艙姿態角速度稍有變化就很容易發生碰撞。因此，只能犧牲載荷艙姿態機動速度以避免兩艙碰撞。

圖6為平臺艙相對太陽基準坐標系姿態，其姿態精度僅達到0.1°，穩定度為5×10-3(°/s)，仿真曲線中的“毛刺”是由于引入了飛輪干擾力矩所引起的。從圖6可以看出，載荷艙的姿態精度和穩定度均遠高于平臺艙，證明了雙體衛星的有效性。從圖7可以看出,八個磁浮機構輸出力在20 s之前發生飽和，之后均未超過飽和閾值0.02 N。從圖8可以看出,磁浮機構的磁鋼和線圈相對運動在姿態機動開始階段最為劇烈，因為姿態機動開始時載荷艙在磁力作用下角加速度較大，而平臺艙為從動控制，相比載荷艙控制指令存在延遲，并且飛輪的帶寬遠遠低于磁浮機構的帶寬，導致了飛輪力矩響應較慢，在姿態機動開始時刻難以跟蹤載荷艙姿態。兩艙磁浮機構相對運動在整個對日定向過程中都保持在±5 mm范圍內，未發生碰撞。從圖9和圖10可以看出，在前20 s，由于兩艙相對位置期望控制力及載荷艙期望控制力矩較大，超出磁浮機構輸出能力，磁浮機構飽和，無法合成期望力及力矩。隨著期望控制力和力矩的減小，在20 s之后磁浮機構可以較好地合成期望力和力矩，驗證了兩艙相對位置和載荷艙姿態協同控制的可行性。

3.2 考慮飛輪動態特性的平臺艙姿態跟蹤控制

為充分說明補償飛輪動態特性對系統控制性能的提升，取飛輪機電常數tws=1 s。平臺艙控制律參數為k=1,k1=diag(1.22,1.22,1.22),k2=diag(28.75,35.63,35.94)。載荷艙控制參數為kpp=0.256,kpd=1.68,ε=1/120。仿真結果圖11～12所示。

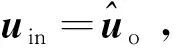
從圖13可以看出，若不對飛輪動態特性進行補償，則在仿真開始階段B1,B2,B3,B4磁浮機構的磁鋼與線圈軸向位移相比于圖12變化更加劇烈，說明補償飛輪動態特性有利于提高平臺艙姿態跟蹤性能。

3.3 載荷艙變增益PD控制

本節針對第2.3節設計的載荷艙變增益PD姿態控制律進行仿真校驗。載荷艙控制律的有關參數選擇如下

仿真結果如圖14所示。

從圖14可以看出，載荷艙700 s左右已完成對日定向。磁浮機構磁鋼與線圈相對位移沒有超過允許閾值。為說明變增益控制策略的優越性，以常規PD控制律對載荷艙姿態控制進行對比仿真。為避免碰撞，姿態機動速度必須限制很小，選擇ε=1/92，其它控制參數與式(26)中的相同。仿真結果如圖16和圖17所示。

從圖16可以看出，載荷艙需要1400 s才能實現對日定向機動控制。圖17表明，B1,B2,B3，B4磁浮機構的線圈和磁鋼軸向運動已接近±5 mm閾值，如果繼續增大控制器參數，將導致兩艙碰撞，說明載荷艙姿態機動角速度已接近極限值。因此采用常規PD控制律的姿態機動速度遠低于采用變增益PD控制律的姿態機動速度，這是由雙體衛星結構特性決定的，充分說明了變增益控制律對于雙體衛星機動的優勢。

4 結 論

本文針對雙體衛星對日定向姿態控制問題，推導了雙體衛星姿態模型及磁浮機構線圈與磁鋼相對位置數學表達式。利用傳統PD控制實現了載荷艙主動對日姿態機動、平臺艙姿態跟蹤的控制目標。在此基礎上，進一步提出了補償平臺艙飛輪動態特性的反步控制律，顯著提高了平臺艙姿態跟蹤速度。在傳統PD控制基礎上，提出一種載荷艙變增益PD控制策略，根據平臺艙姿態跟蹤情況調整載荷艙姿態機動速度，有效提高了兩艙的協同控制性能，進而提高了雙體衛星整體的姿態機動速度。