基于變論域模糊方法的電力推進船舶二次調(diào)頻控制

李洪躍，王錫淮，肖健梅

上海海事大學(xué)物流工程學(xué)院，上海201306

0 引 言

船舶綜合電力系統(tǒng)將船舶動力系統(tǒng)與電力系統(tǒng)結(jié)合起來，在優(yōu)化船舶結(jié)構(gòu)布局，提高燃油經(jīng)濟性和故障容錯率等方面體現(xiàn)出巨大的優(yōu)勢，已成為未來艦船發(fā)展的主要方向［1］。隨著船舶發(fā)展的大型化和多用途化，不僅要求船舶電力系統(tǒng)在復(fù)雜多變的水域環(huán)境和快速大功率擾動下保持穩(wěn)定，同時還要求其具有較高的能量利用率和較低的氣體排放。因此，將可再生能源和儲能單元引入船舶電力系統(tǒng)組成的混合電力推進系統(tǒng)［2-5］，受到了廣泛的關(guān)注。

在船舶電力系統(tǒng)工作的過程中，負載功率變化以及可再生能源功率的不穩(wěn)定輸出，會造成電力系統(tǒng)輸出功率與需求功率不匹配，從而引起負荷頻率波動；系統(tǒng)頻率不穩(wěn)定，將影響船舶通信導(dǎo)航等設(shè)備的正常工作，嚴重情況下會導(dǎo)致電力系統(tǒng)崩潰。由于混合電力推進船舶作為一個離岸孤立運行的系統(tǒng)，與陸地微電網(wǎng)系統(tǒng)具有一定的共性，因此針對頻率控制的相關(guān)方法可以借鑒。米陽等［6-7］針對光柴互補的孤立微電網(wǎng)系統(tǒng)，提出了一種基于負荷估計的滑模控制方法。通過對擾動功率的估計和電網(wǎng)頻率變化，設(shè)計滑模補償控制器，對柴油發(fā)電機組輸出的有功功率進行控制。該控制方法具有較好的魯棒性，并且降低了控制器設(shè)計的成本。Liu等［8-10］針對線性化的負荷頻率控制模型，采用模型預(yù)測控制（MPC），對分布式微電網(wǎng)系統(tǒng)的頻率波動進行控制，通過反饋校正和滾動優(yōu)化過程，使得該控制方法具有較好的抗干擾能力和實時性，但是電力系統(tǒng)是一個非線性時變的不確定系統(tǒng)，模型預(yù)測控制對此系統(tǒng)的控制問題并沒有很好地解決。Sun等［11-12］針對將可再生能源引入到電網(wǎng)系統(tǒng)中引起的功率波動，考慮通信網(wǎng)絡(luò)對微電網(wǎng)二次調(diào)頻控制帶來的時滯影響，設(shè)計基于線性矩陣不等式的輸出反饋魯棒控制，利用李雅普諾夫理論，建立了線性矩陣不等式約束條件，通過求解得到時滯狀態(tài)反饋控制器。Bevrani等［13-14］針對多能源組成的分布式微電網(wǎng)系統(tǒng)，采用基于H∞和μ綜合方法的魯棒控制設(shè)計二次頻率控制器，分別利用線性矩陣不等式和DK迭代方法進行控制器的求解，并在頻域內(nèi)驗證了所設(shè)計控制的魯棒穩(wěn)定性和魯棒性能。該控制方法對系統(tǒng)在外部擾動和內(nèi)部參數(shù)攝動情況下引起的頻率波動具有較好的控制性能，但由于所設(shè)計控制器的階數(shù)較高，增加了控制器設(shè)計的成本。以上方法針對陸地由多能源組成的微電網(wǎng)系統(tǒng)的二次調(diào)頻控制取得了較好的控制效果，所設(shè)計的控制器具備較好的魯棒性和控制精度。但上述控制方法的設(shè)計都需要基于精確的數(shù)學(xué)模型，而電力系統(tǒng)中由外部擾動和參數(shù)攝動引起的負荷擾動是一個難以建模的非線性系統(tǒng)。在陸地電網(wǎng)中，由于機組容量可以看作無限大系統(tǒng)，建模過程中的近似線性化并不影響系統(tǒng)的整體性能，而在船舶電力系統(tǒng)中，負荷電機和發(fā)電機通常具有相同的容量，電機的啟停和變負荷運行會對系統(tǒng)的穩(wěn)定運行造成巨大影響，同時受風(fēng)浪的影響，系統(tǒng)發(fā)電側(cè)的輸出功率和用電側(cè)的需求功率不能保持平衡。雖然上述控制策略對船舶微電網(wǎng)的二次頻率控制具有一定的借鑒性，但是難以保證控制器的魯棒性和控制精度，或者還會增加設(shè)計成本。

模糊控制通過采用不確定或者不精確的語言描述已知信息，并將其轉(zhuǎn)換為控制行為，對類似電力系統(tǒng)中具有外部擾動和難以建模的參數(shù)攝動模型具有較好的控制效果，在解決微電網(wǎng)的二次調(diào)頻控制中可以得到較滿意的控制效果［15-16］。同時，模糊控制的控制精度受其隸屬度函數(shù)的影響，控制精度越高，要求的控制規(guī)則越多，這對于以工程人員的經(jīng)驗和專家知識來總結(jié)控制規(guī)則的模糊控制器來說是無法做到的。因此，從某種意義上說，模糊控制屬于一種粗糙的控制方式。

基于以上分析，本文將以包含儲能單元的船舶電力系統(tǒng)為研究對象，在考慮外部負荷擾動和參數(shù)攝動的情況下，采用變論域模糊方法設(shè)計控制器進行調(diào)頻控制。通過引入伸縮因子，使模糊控制中隸屬度函數(shù)的論域具有根據(jù)輸入量大小自動調(diào)節(jié)范圍的能力，從而提高控制器的控制精度。最后通過仿真實驗，驗證該方法的正確性和合理性。

1 模型描述

混合電力推進船舶由柴油發(fā)電機組、蓄電池、交流母線、電氣負載和推進器組成，其結(jié)構(gòu)布局如圖1所示。

其中，柴油發(fā)電機組作為最主要的能量源，通過原動機帶動同步發(fā)電機輸出三相交流電。電池利用其快速充放電特性，平衡負載功率和柴油發(fā)電機輸出功率之間的差值。交流母線承載柴油發(fā)電機組和蓄電池的輸出功率，通過變壓過程為負載供電。系統(tǒng)負載主要包括電動機帶動的螺旋槳負載和其他電氣負載，如伺服泵、側(cè)推器和導(dǎo)航設(shè)備等。

在船舶運行過程中，當(dāng)主推進電機及其螺旋槳啟/停與變負荷運行，以及側(cè)推器或者服務(wù)泵機等大功率電機啟/停與變負荷運行時，將對船舶電網(wǎng)產(chǎn)生較大沖擊。當(dāng)負荷功率變化時，發(fā)電機的電轉(zhuǎn)矩會發(fā)生變化，引起柴油機機械轉(zhuǎn)矩和電轉(zhuǎn)矩的不平衡，導(dǎo)致發(fā)電機在運行的過程中轉(zhuǎn)速發(fā)生變化，最終使得電網(wǎng)的頻率波動與發(fā)電機有功功率輸出不穩(wěn)定。保持船舶電網(wǎng)功率平衡，可表示為

式中：ΔP為船舶電網(wǎng)功率變化；ΔPdeg為柴油發(fā)電機組輸出功率變化；ΔPbat為電池功率變化，當(dāng)電池輸出功率時為正，電池吸收功率時為負；ΔPload為系統(tǒng)擾動功率。當(dāng)系統(tǒng)頻率波動不大時，首先利用調(diào)速器的調(diào)速特性進行一次調(diào)頻，但是一次調(diào)頻為有差調(diào)頻，在頻率波動較大的情況下無法將頻率恢復(fù)到基準值，因此必須使用二次調(diào)頻功能使頻率保持穩(wěn)定。對系統(tǒng)的頻率進行控制，本質(zhì)上是對柴油機組的轉(zhuǎn)速進行控制，忽略調(diào)速過程對發(fā)電機勵磁的影響，單機組的頻率控制模型如圖2所示。

系統(tǒng)各組件經(jīng)拉氏變換后，用一階慣性模型表示如下。

調(diào)速機環(huán)節(jié)：

原動機環(huán)節(jié)：

發(fā)電機環(huán)節(jié)：

式中：s為拉普拉斯算子；ΔXg為調(diào)速機輸出；Tg為調(diào)速機時間常數(shù)；Δu為系統(tǒng)輸入；Δf為系統(tǒng)頻率偏差；R為下垂系數(shù)；Tdeg為原動機時間常數(shù)；M為慣性系數(shù)；D為阻尼系數(shù)。

電池模型采用文獻［17］建立的輸入輸出模型，為進一步掌握電池剩余容量，在其基礎(chǔ)上加入了電池荷電狀態(tài)（SOC）輸出環(huán)節(jié)，其模型結(jié)構(gòu)如圖3所示。其輸入為二次頻率控制信號，輸出為電池輸出功率ΔPb。

圖中：C0表示電池初始容量；Cmin表示電池容量下限；Cmax表示電池容量上限，通過對電池容量上、下限的限定，使電池避免出現(xiàn)過充過放的現(xiàn)象，保證電池的安全性和使用壽命；Gb(s)表示電池經(jīng)過拉氏變換后的一階慣性環(huán)節(jié)，

式中，Tb為電池時間常數(shù)。

2 變論域模糊控制

2.1 論域的變換

模糊控制以模糊語言為基礎(chǔ)，非常適用于非線性系統(tǒng)。但是要得到較高精度的模糊控制器，則需要控制規(guī)則足夠充分，這對于工程人員來說非常困難。因此，郭海剛等［18］提出了變論域模糊控制。

考慮多輸入單輸出的模糊控制器，設(shè)Xi=[-Ei,Ei],(i=1,2,…)，為輸入量xi的論域，Y=[-U,U]，為輸出量y的論域，其中Ei和U均為正實數(shù)，為Xi和Y的初始論域。變論域是指Xi和Y隨變量xi，y的變化而調(diào)整，即

式中，αi(xi)和β(y)為論域的伸縮因子，如圖4所示。

從圖4中可以看出，通過選擇合理的伸縮因子使得論域進行改變，在規(guī)則不變的前提下，論域的縮小和放大相當(dāng)于規(guī)則的增加和減少，從而提高控制精度。

2.2 伸縮因子的設(shè)計

變論域模糊控制效果的優(yōu)劣，最主要的是伸縮因子的設(shè)計和選擇。系統(tǒng)誤差的狀態(tài)是確定伸縮因子的主要因素，當(dāng)系統(tǒng)誤差較大時，選擇原始控制規(guī)則粗略控制，此時α(x)趨向于1；當(dāng)誤差減小時，控制規(guī)則應(yīng)隨誤差變化適當(dāng)加密，使誤差收斂速度適當(dāng)加快，因此α(x)也應(yīng)適當(dāng)變小；當(dāng)誤差變得很小趨于0時，控制規(guī)則應(yīng)隨之變得精密，以進行精確控制，因此伸縮因子也應(yīng)趨于0。伸縮因子的選擇，需要同時滿足避零性、單調(diào)性、協(xié)調(diào)性、正規(guī)性和對偶性原則［19］。

為此，采用增量法設(shè)計伸縮因子［20］。假定x的增量為Δx，則相應(yīng)的α增量為Δα，近似認為Δx與Δα成正比。同時，對于同樣大的增量Δx，若x越大，Δα應(yīng)越小；由于α不超過1，所以α越接近1，Δα應(yīng)越小，則

通過求解，得到伸縮因子的函數(shù)表達式為

從式中可以看出，當(dāng)|x|趨向于E時，有α＞0；當(dāng) |x|趨向于0時，同樣有α＞0。因此，伸縮因子的選取滿足設(shè)計原則。進一步對式（8）關(guān)于x求導(dǎo)，則有

當(dāng)|x|趨向于E時，趨于0；當(dāng) ||x趨向于0時，趨于λk，通過選擇合適的k，使得α具有較大值。因此，式（8）所示的伸縮因子既滿足基本設(shè)計原則，又同時滿足優(yōu)化設(shè)計準則，具有較好的使用效果。

3 模糊控制器的設(shè)計

模糊控制器設(shè)計為兩輸入單輸出的響應(yīng)函數(shù)，以頻率偏差信號e(t)+eset(t)及其變化率作 為 模 糊 控 制 的 輸 入 信 號 ，其 中e?(t)＜0，eset(t)為由限速器約束得到的誤差門檻值。控制器輸出為系統(tǒng)二次頻率控制信號，控制信號作用于調(diào)速機，通過改變調(diào)速機的調(diào)速特性來改變有功功率輸出，使得系統(tǒng)頻率回到設(shè)定值，同時電池通過充、放電過程減小系統(tǒng)頻率波動。伸縮因子通過輸入的誤差信號及其變化率的大小，來對模糊控制器的隸屬度函數(shù)進行自適應(yīng)調(diào)整。加權(quán)因子τ1，τ2對輸入信號進行調(diào)節(jié)，以獲得控制器較好的輸出性能，其輸入輸出關(guān)系如圖5所示。

模糊控制器對負荷頻率的控制過程分為3步：

1）對系統(tǒng)變量模糊化。對系統(tǒng)的輸入輸出信號進行模糊化，構(gòu)成模糊集。通過隸屬度函數(shù)，計算出輸入量及輸出量的隸屬度，將輸入量e(t)與劃分為 7個等級的模糊子集：｛NB｝，｛NM｝，｛NS｝，｛Z｝，｛PS｝，｛PM｝，｛PB｝，分別對應(yīng)為｛負大｝、｛負中｝、｛負小｝、｛零｝、｛正小｝、｛正中｝、｛正大｝，輸入變量的論域變化范圍根據(jù)長期統(tǒng)計確定；輸出量同樣按照隸屬度函數(shù)劃分為7個等級的 模 糊 子 集 ：｛NB｝，｛NM｝，｛NS｝，｛Z｝，｛PS｝，｛PM｝，｛PB｝。系統(tǒng)的隸屬度函數(shù)如圖6所示，每一個隸屬度函數(shù)的取值范圍為［0，1］。系統(tǒng)變量的論域范圍視輸入輸出的變化情況而定，通過伸縮因子，可以保證系統(tǒng)變量論域有較好的自適應(yīng)性。其中e(t)的論域范圍為的論域范圍為

2）模糊推理過程。根據(jù)系統(tǒng)變量模糊化過程，按照負荷頻率控制要求，確定模糊控制規(guī)則，如表1所示。

表1 模糊控制規(guī)則Table 1 Fuzzy control rules

根據(jù)表1所示規(guī)則，可以得到模糊子集表示的輸出量。

3）反模糊化。將模糊推理得到的被控量轉(zhuǎn)化為實際控制的精確量，模糊控制得到的控制器輸出量經(jīng)過反模糊化變換成表示在論域范圍內(nèi)的精確量，再將論域內(nèi)的精確量變換為實際的控制信號。

4 仿真驗證

為了驗證基于變論域模糊控制的混合電力推進船舶負荷頻率控制，根據(jù)式（2）～式（5）描述的負荷頻率控制模型在Matlab/Simulink環(huán)境中搭建仿真模型。采用文獻［21-23］中的系統(tǒng)模型參數(shù)，如表2所示。

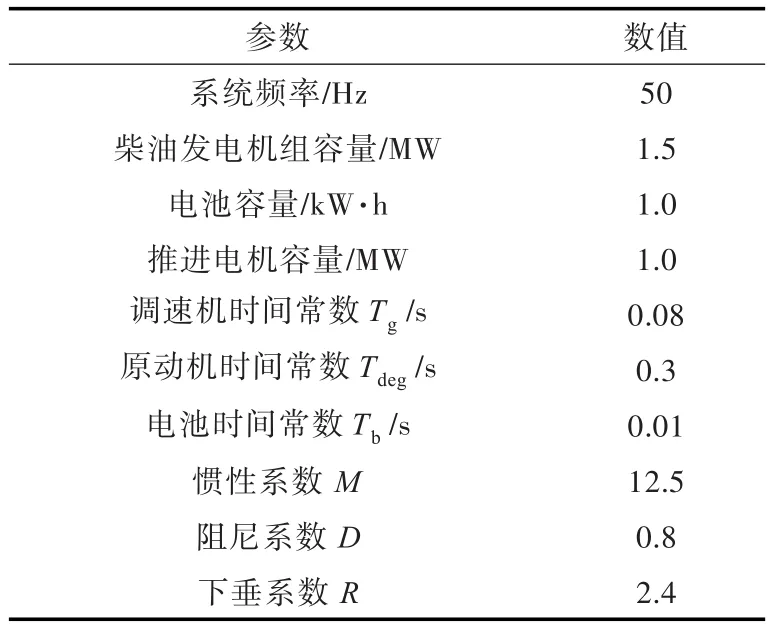
表2 系統(tǒng)參數(shù)Table 2 System parameters

首先，圖7所示為接入電池的混合電力系統(tǒng)與沒有接入電池的電力推進系統(tǒng)在傳統(tǒng)PID控制方法下的動態(tài)響應(yīng)輸出對比，假設(shè)系統(tǒng)受到階躍擾動功率ΔPload=0.1 p.u.，電池初始SOC設(shè)定為0.6，SOC上限設(shè)定為0.9，下限設(shè)定為0.1，在仿真過程中加入限制約束，避免電池出現(xiàn)過充過放現(xiàn)象。從圖7中可以看出，通過把電池引入船舶電力系統(tǒng)，明顯降低了系統(tǒng)負荷頻率波動次數(shù)，縮短了系統(tǒng)恢復(fù)穩(wěn)定時間。同時在引入電池的系統(tǒng)中，通過電池對系統(tǒng)擾動功率的響應(yīng)特性，降低了柴油機組功率輸出變化。從結(jié)果中可以看出，引入電池的系統(tǒng)中柴油機組輸出功率要大于未引入電池的電力系統(tǒng)，這是因為傳統(tǒng)的PID控制方法局限于對柴油發(fā)電機組的功率控制，而并未考慮電池對系統(tǒng)的影響，導(dǎo)致柴油機過多地輸出功率為電池充電。

其次，為了驗證變論域模糊控制的合理性，以傳統(tǒng)模糊控制作為對比，假設(shè)系統(tǒng)受到階躍擾動功率ΔPload=0.1 p.u.，在電池SOC設(shè)定不變的情況下，輸出響應(yīng)如圖8所示，圖中，VUFC為變論域模糊控制曲線，F(xiàn)C為模糊控制曲線。從圖中可以看出，在變論域模糊控制下，系統(tǒng)由于外部功率擾動產(chǎn)生的頻率波動范圍明顯小于傳統(tǒng)模糊控制，其頻率在5 s左右就已經(jīng)恢復(fù)到基準值，而傳統(tǒng)模糊控制在系統(tǒng)產(chǎn)生的超調(diào)量和收斂時間上均劣于變論域模糊控制。同時，由于負荷功率變化導(dǎo)致系統(tǒng)輸出功率與需求功率不平衡，系統(tǒng)通過二次調(diào)頻控制器改變調(diào)速機的調(diào)速特性，在變論域模糊控制下柴油機輸出功率能在較短的時間內(nèi)再次達到穩(wěn)定。從電池SOC變化曲線可以看出，電池通過其充、放電功能吸收了電網(wǎng)中的擾動功率，減少了柴油發(fā)電機組的功率調(diào)節(jié)。同時在變論域模糊控制下，電池SOC的改變量較小，進一步避免了電池產(chǎn)生過充過放現(xiàn)象，提高了電池安全性。

最后，驗證系統(tǒng)在參數(shù)攝動情況下的輸出響應(yīng)。假設(shè)系統(tǒng)模型參數(shù)具有±20%的攝動范圍，在相同電池狀態(tài)下，系統(tǒng)的主要輸出響應(yīng)如圖9所示。由于系統(tǒng)因工作環(huán)境導(dǎo)致的參數(shù)攝動是難以建模和測量的，在這種情況下，由于模糊控制基于不確定信息得到的控制器仍然具有較好的魯棒性能。從圖中可以看出，在參數(shù)攝動情況下，傳統(tǒng)模糊控制和變論域模糊控制仍然能保證系統(tǒng)頻率恢復(fù)穩(wěn)定，但相比于外部擾動情況，增加了其恢復(fù)穩(wěn)定的時間，變論域模糊控制在8 s時間內(nèi)恢復(fù)穩(wěn)定，傳統(tǒng)模糊控制則需要14 s的時間。柴油機組的輸出功率相比于圖8變化更劇烈，但最終仍然可以保證穩(wěn)定輸出。從電池SOC的變化曲線可以看出，由于參數(shù)攝動的不確定性，增加了電池輸入輸出功率的變化，相比于圖8，SOC的改變量加大了。

從以上實驗可以看出，引入電池組成的混合式電力推進系統(tǒng)，通過電池的充、放電功能可以進一步保證系統(tǒng)頻率的穩(wěn)定性，減小柴油發(fā)電機組輸出功率的波動，間接提高柴油機組的燃油經(jīng)濟性。基于變論域模糊控制在外部擾動和系統(tǒng)參數(shù)攝動情況下，相比于傳統(tǒng)模糊控制，具有較好的魯棒穩(wěn)定性和魯棒性能。

5 結(jié) 語

本文針對船舶電力推進系統(tǒng)，為解決由負荷功率擾動和系統(tǒng)參數(shù)攝動情況下引起的系統(tǒng)頻率波動，采用模糊控制方法設(shè)計二次頻率控制器。首先建立包含電池儲能的船舶電力系統(tǒng)負荷頻率控制模型；然后為了提高模糊控制的控制精度，引入伸縮因子對隸屬度函數(shù)論域范圍進行了調(diào)整，使控制器隸屬度函數(shù)具有跟隨輸入誤差自適應(yīng)變化的能力；最后設(shè)計仿真實驗進行驗證，結(jié)果表明引入電池儲能可以明顯提高系統(tǒng)穩(wěn)定性，變論域模糊控制可保證系統(tǒng)頻率具有較小的超調(diào)量和較短的穩(wěn)定時間，保證系統(tǒng)的魯棒穩(wěn)定性和魯棒性能。