局部優先的社會網絡社區結構檢測算法*

李春英，湯志康+，湯 庸，趙劍冬，黃泳航

1.廣東技術師范學院 計算機科學學院，廣州 510665

2.華南師范大學 計算機科學學院，廣州 510631

1 引言

隨著網絡技術、智能終端以及計算交流技術的快速發展，社會網絡（social network service，SNS）已經成為互聯網時代最具影響力的應用。這些以人為中心的社會網絡是智能化程度很高的復雜網絡，受人的世界觀、生活環境、所處位置、興趣愛好等的影響，其遵循著“物以類聚、人以群分”（社區結構）的特點。而在真實社區結構中，一些用戶可能同時屬于親人社區、朋友社區、興趣愛好社區等多個不同的社區，這樣的社區稱之為重疊社區。重疊社區檢測研究為在線社會網絡的推薦系統[1-2]、鏈接預測[3-4]、異質網絡分析[5]、社會網絡演變[6]等提供決策性支持，使社會網絡在為用戶提供優質服務的同時也為其保持用戶的粘性和持續活躍度提供了幫助。

社區檢測也叫作社區聚簇，近十年已成為計算機、物理、生物、社會學以及復雜性系統科學等多學科的研究熱點。學者們從不同角度對社區檢測算法進行了嘗試，如模塊度算法[7-8]、層次聚類算法[9-10]、基于k-clique的算法[11-12]、基于鏈接聚類的算法[13-14]、基于局部優化和擴展的算法[15]以及基于標簽傳播的算法（label propagation algorithm，LPA）[16]等。其中，基于標簽傳播的社區檢測算法提出了一個很好的視角，采用信息傳播來確定復雜網絡中的社區結構。因其簡單易行而受到學者的廣泛關注。LPA算法采用獨一無二的標簽對網絡中的節點進行初始化，在每一步標簽更新中，節點吸收其鄰居節點最大的標簽。這種基于agent和分散的方法使LPA算法不需要先驗知識且擁有近似線性的時間復雜度，因而能夠適應于擁有百萬級節點的復雜網絡[17]。但是LPA算法的異步更新方式導致其具有較弱的健壯性。針對這個問題，文獻[18]結合同步更新和異步更新策略，提出LPA算法的半同步更新版本。實驗結果表明該算法提高了LPA算法的性能和健壯性。文獻[19]綜合考慮頂點鄰居中相同標簽所占比例、頂點度數和邊的權重等信息來計算每個頂點的標簽影響值并更新頂點的標簽。文獻[20]提出LPA算法的同步更新版本（synchronous version of LPA，LPA-S）。LPA-S算法使用獨一無二的標簽對復雜網絡中的節點進行初始化，并提出概率更新策略避免在同步更新時產生標簽振蕩現象。但是，文獻[16-20]均是針對復雜網絡非重疊社區的檢測算法。

實際上，社區重疊是真實復雜網絡非常重要的特征，重疊節點在復雜網絡中通常扮演著重要的角色[21]。因此，文獻[22]提出了多標簽同步傳播算法（community overlap propagation algorithm，COPRA）檢測復雜網絡中的重疊社區結構。該算法繼承了LPA算法時間復雜度低、適用大型網絡等優點。但是其通過輸入參數v控制節點所屬的社區個數，這難于適應節點所屬社區個數差異較大的真實社會網絡。另外，一些算法[23-24]的實驗結果表明，COPRA算法在一些復雜網絡的社區劃分結果中存在過擬合現象，即社區劃分結果產生了一個包含所有節點的大社區。文獻[23]提出了最小極大團標簽傳播算法（minimal maximal clique label propagation algorithm，MMCLPA）檢測復雜網絡中的重疊社區結構。該算法采用最小極大團及自適應閾值的方式提高了算法的質量并克服了預先輸入參數對未知復雜網絡的局限性等問題。但文獻[25]在真實社會網絡中的實驗結果表明MMCLPA算法的自適應閾值偏小，可能導致一些社會網絡的社區檢測結果中存在過多重疊節點。另外，MMCLPA算法中可能存在同步和異步兩種標簽更新方式，這可能引起不穩定的社區檢測質量。劉世超等[26]提出一種基于標簽傳播概率的重疊社區發現算法（label-propagation-probability-based，LPPB），LPPB算法根據節點的影響力大小進行更新，綜合網絡結構的傳播特性、節點的屬性特征和歷史標簽記錄信息等計算及修正標簽的傳播概率及更新結果。和COPRA算法一樣，LPPB算法通過輸入參數調整節點可以擁有的最大標簽數，預先輸入參數的方法使得LPPB算法很難適應各種類型真實社會網絡的社區結構檢測。

基于以上研究以及文獻[27-28]提出的在微觀層次上更加易于檢測高質量的社區結構等觀點，提出基于微觀結構極大團的同步自適應標簽傳播算法（synchronous adaptive label propagation algorithm，ALPA-S）和異步自適應標簽傳播算法（asynchronous adaptive label propagation algorithm，ALPA-A）檢測社會網絡中的社區結構。本文的主要貢獻可以概括為兩點：（1）兩種算法均以微觀結構極大團作為社區結構的核心，通過相應更新規則實現節點的標簽更新，算法全程不需要參數控制，極大團中節點數和標簽權重閾值均會根據網絡拓撲結構及節點標簽個數的不同而自動調整，使算法能夠更好地適應多種拓撲結構類型的社會網絡。（2）兩種算法均可用于檢測社會網絡中的重疊社區和非重疊社區，具有良好的適應性。

2 ALPA-S算法

2.1 初始化

k-core[29]是圖論中一個非常重要的概念，其被廣泛應用于網絡結構可視化[30-31]，解釋社會網絡的協同過程[32-33]，分析復雜網絡中節點的層次和連通性[34]以及分析復雜網絡的發展和演化[35]等。在社區檢測方面，常常利用k-core作為子路線解決復雜網絡中的難題，如計算k-clique、計算連接關系緊密的子圖以及求解至少k度子圖（at-least-k-subgraph）的問題等[36-37]。考慮到社會網絡中影響力大的節點對社區的形成具有一定的促進作用以及基于微觀角度更加易于檢測社區結構等問題，提出基于網絡拓撲結構度量節點的影響力，并按照節點影響力強弱在社會網絡中依次尋找局部極大團（如定義1），并為極大團中的節點賦予標簽及權重。

定義1（極大團）社會網絡被模型化為圖G={V,E}的形式，其中V表示社會網絡節點集合，E表示節點間相鄰關系集合。每個節點vi(vi∈V)都有一個標簽集合Ci,N(vi)是節點vi的鄰居節點集合，|N(vi)|代表節點vi的影響力。以V中Ci=的影響力最大節點vi及N(vi)中標簽集為空的影響力最大節點vj構成的邊(vi,vj)為初始邊，按照節點影響力強弱構建完全圖Gm，稱Gm為團。若Gm?G，且不存在完全圖Gt?G，使得Gm?Gt，則稱Gm為極大團（maximal clique），簡稱MC。

按照定義1，一個極大團至少包含3個節點。實際上，文獻[25]已經表明3個節點可以構成一個小型社區。同時，為了降低算法的運行時間以及避免類似CPM算法[11]在稠密復雜網絡中尋找全部極大團耗費大量時間等問題，提出的極大團在復雜網絡中是唯一的，即任何兩個極大團間的交集為空集。結合定義1，ALPA-S算法標簽初始化過程如下所示。

（1）對于社會網絡中的任一節點vi的標簽集Ci，設置Ci←? ；

（2）c←1；

（3）按照定義1尋找MC，對MC中的每一個節點vi的標簽集Ci，令Ci←{(c,1)}；

（4）c←c+1；

（5）重復步驟（3）、（4），直到沒有滿足要求的節點為止。

按照算法初始化規則，ALPA-S算法在圖1所示的復雜網絡中共找到2個極大團，分別為(a,b,c)和(e,g,f)。并且極大團(a,b,c)中節點標簽和權重均為1；極大團(e,g,f)中的節點標簽均為2，權重也均為1。如圖1所示。初始化后MC中的節點均擁有了標簽和權重，而非MC節點則沒有獲得標簽和權重。根據復雜網絡小世界模型，只要節點擁有鄰居，則在算法標簽更新中可使其獲得標簽。

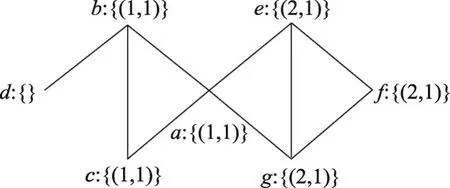
Fig.1 Complex network initialized graph圖1 復雜網絡初始化結果圖

2.2 迭代過程

復雜網絡初始化后，一些節點獲得了標簽和權重，這些標簽和權重成為算法迭代開始時的種子。算法迭代時，節點繼承其所有鄰居節點的標簽及按照權重更新規則產生的權重值。通過對復雜網絡拓撲結構及節點所屬社區情況的深度分析可知，節點是否屬于某個社區與節點在該社區對應標簽下的權重有關，而節點在某個標簽下的權重值則與節點在該標簽下的度數分布情況有關。例如，復雜網絡中的一個5度節點vi，其中4度貢獻給了社區1，說明在vi的5個關系中與社區1中的節點有4條連接關系；1度貢獻給了社區2，說明vi的5個關系中與社區2中的節點有1條連接關系。直觀上講，該節點vi應該更大程度上屬于社區1，而不屬于社區2。因此，標簽權重的計算方法需要充分考慮節點度數在各個標簽下的分布并且要避免某個鄰居節點標簽權重過大產生的“吞噬”問題。根據以上分析，提出權重計算公式（1）。假設函數bt(c,vi)表示在第t輪迭代時標簽c在節點vi下的權重值。在ALPA-S算法中，權重的更新方法如式（1）所示。

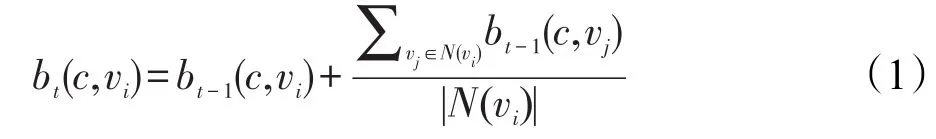
其中，N(vi)表示節點vi所有鄰居節點的集合。節點vi在第t-1步已經擁有標簽c，則節點vi在第t步更新時，如果其鄰居節點vj也擁有標簽c，則節點vi在第t步標簽c下的權重值為其在第t-1步標簽c的權重值與其鄰居節點vj在第t-1步標簽c的權重值與節點vi度數的比值之和。若被更新節點vi中第t步沒有鄰居節點的標簽c，則bt-1(c,vi)值為0。節點vi接收鄰居節點的標簽c作為新標簽，并按照式（1）計算標簽c對應的權重。

另外，考慮到社區結構的局部性以及為了避免無效標簽被傳播得更遠，ALPA-S算法在每次迭代后對所有節點下的標簽進行處理。COPRA算法將預先輸入參數v的倒數作為節點標簽是否有意義的判斷閾值。與參數v并不一定適用于社會網絡中所有節點一樣，將作為所有節點標簽權重是否有意義的判斷閾值也不一定合適。受COPRA算法的啟發，將作為節點標簽是否有意義的判斷條件。與COPRA算法不同的是是一個與每個節點的標簽個數L有關的變量，把這個變量叫作自適應閾值，具體如定義2所示。

定義2（自適應閾值）如果一個節點vi擁有L個標簽，則每個有意義標簽的權重值應該大于等于即為節點vi對應的權重閾值。每個節點在每次迭代后擁有的標簽個數不同，權重閾值因此也不同。把隨著節點標簽個數發生變化的變量叫作自適應閾值。

ALPA-S算法迭代過程如下所示。

（1）t←1。

（2）按照式（1）更新節點的標簽及權重。

（4）歸一化所保留節點的標簽權重，使其和為1。

（5）如果每個節點都擁有了標簽，則算法停止。

（6）否則t←t+1，重復步驟（2）～（5）。

按照算法的迭代規則，對圖1復雜網絡初始化結果進行第1輪迭代后，節點標簽權重的一種更新結果為同時，按照自適應閾值剔除無意義的標簽及權重。具體過程為：僅有一個標簽的節點不作處理，包含2個及以上標簽的節點為e、g、f、a。其中，節點e有兩個標簽，因此對應的自適應閾值為，刪除標簽權重小于的標簽權重有序對，則節點e僅剩下標簽2，為其余3個節點g、f、a與節點e自適應閾值相同，使用類似的方法刪除權重小于的標簽權重有序對，結果為最后對所有節點的標簽權重歸一化處理，結果為圖2顯示了ALPAS算法按照標簽更新規則迭代1次后并進行歸一化處理后的結果。

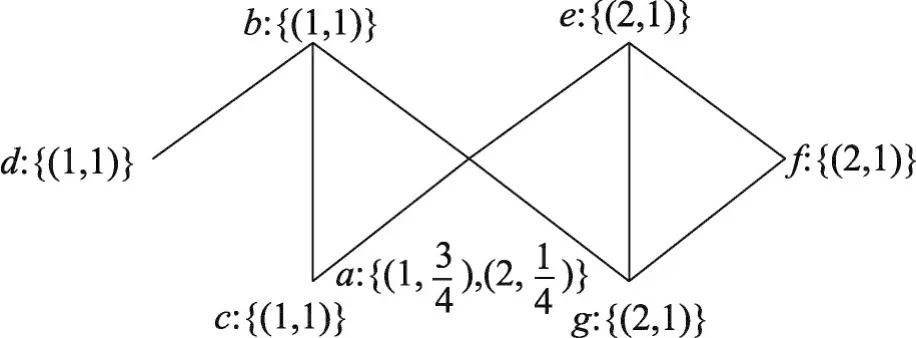
Fig.2 Propagation of labels:first iteration圖2 第1次標簽傳播后的復雜網絡結果圖

2.3 終止條件

考慮到社區結構的局部性以及離極大團較遠的節點擁有標簽即達到了局部社區劃分的目的，使用所有節點擁有標簽作為ALPA-S算法迭代終止的條件。這個終止條件可以使標簽在有意義的局部范圍內傳播并有效減少算法的迭代次數，同時可以避免同步更新算法（如DLPA[38]）為了達到穩定狀態而產生的標簽振蕩問題以及過擬合現象等。按照這個終止條件，圖1所示復雜網絡在第1次迭代后，所有節點都擁有了標簽，則ALPA-S算法終止。

2.4 后期處理

在ALPA-S算法中，標簽的數量是復雜網絡中不相交極大團的數量。隨著迭代過程的推進，標簽數量逐漸減少。當算法終止時，剩余標簽的數量代表復雜網絡中的社區個數，一個標簽代表一個社區。如果一個節點擁有至少兩個標簽（即標簽集長度|Ci|＞1），表明該節點同時屬于至少兩個社區，則該節點為重疊節點，如定義3所示。按照此規則，圖2所示的迭代結果包含兩個社區：社區1{a,b,c,d}和社區2{a,e,f,g},則a為重疊節點。但是，按照這種方法形成的社區往往會存在一些子集社區。如在社區結果中有兩個不同的社區Ci和Cj，分別為Ci={v1,v2,v3,v4},Cj={v1,v2,v3,v4,v5}。不難看出社區Ci是社區Cj的子集。顯然,保留社區Cj更有意義。因此，ALPA-S算法按照定義4的規則處理社區檢測結果中的子集社區。

定義3（重疊節點）Ci和Cj是兩個不同的社區，若節點vi同時屬于社區Ci和Cj，則稱節點vi為重疊節點。即：overlap(vi)??vi(vi∈Ci∩Cj∧Ci≠Cj)。

定義4（社區處理）若存在社區Ci和并且Ci?Cj，則刪除社區Ci，保留社區Cj。

2.5 時間復雜度

假設復雜網絡中有n個節點且節點的平均度數為k,有H個極大團且極大團平均節點數為m。ALPAS算法的時間復雜度主要分為三部分：（1）初始化過程；（2）迭代過程；（3）后期處理。

ALPA-S算法在初始化階段設置網絡中節點vi的標簽集Ci=Φ，時間復雜度為O(n)；之后按照定義1尋找網絡中的MC，尋找MC過程產生的時間復雜度為因此，ALPA-S算法整個初始化過程產生的時間復雜度為

假設ALPA-S算法收斂時需要的迭代次數為T,每個節點更新標簽分為3個過程：

（1）按照式（1）更新當前節點的標簽及權重；

（2）對更新后的節點標簽進行處理；

（3）對節點保留標簽的權重進行歸一化處理。

因此，ALPA-S算法迭代過程的時間復雜度為O(Tkn)。

ALPA-S算法后期處理過程產生的時間復雜度為O(n)。

3 ALPA-A算法

考慮使用異步標簽傳播方式會使算法更快收斂，提出異步自適應標簽傳播算法（asynchronous adaptive label propagation algorithm，ALPA-A）。ALPAA算法的初始化過程、后期處理過程與ALPA-S算法相同。不同之處在于ALPA-A算法采用異步更新方式，具體更新規則如式（2）所示。

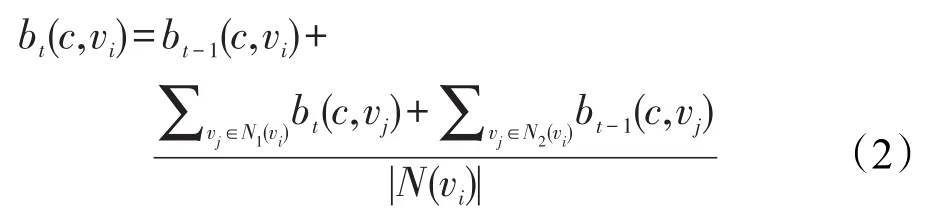
其中，bt-1(c,vi)為節點vi在第t-1步被更新的結果。N(vi)為節點vi的鄰居節點集合，N(vi)=N1(vi)∪N2(vi)，且N1(vi)∩N2(vi)=?。N1(vi)中的節點在第t步已經被更新，N2(vi)中節點的最新結果則是在第t-1步被更新。如果節點vi的鄰接節點vj在第t步被更新，則更新節點vi的標簽及權重時使用節點vj最近被更新的結果。否則使用其在第t-1步的更新結果。ALPAA與ALPA-S只是算法迭代過程采用的更新規則不同。盡管兩種算法收斂時的迭代次數可能不同，但它們的時間復雜度是一致的。

4 實驗

4.1 實驗數據和評價方法

通過兩種方式評估算法的性能：一種是使用仿真網絡生成程序LFR[39]生成帶有重疊社區和非重疊社區的仿真網絡數據集；另一種是使用現實生活中真實的社會網絡數據集。實驗環境為Win 7 OS、Intel?Core? i5 3.20 GHz處理器，算法實現為Python2.7程序設計語言，算法評價環境為Eclipse平臺下的Java語言，數據集格式均為文本文檔。

4.1.1 仿真網絡數據和評價方法

LFR仿真網絡生成程序在產生仿真網絡數據的同時也產生了社區劃分的結果，方便算法使用其生成的仿真網絡數據集進行社區劃分的結果與已知社區進行對比。利用LFR產生的仿真網絡數據集如表1所示。其中，n表示仿真網絡中的節點數，k是仿真網絡節點的平均度數。kmax表示仿真網絡中節點度數的最大值。Cmin表示仿真網絡社區長度的最小值。Cmax表示仿真網絡社區長度的最大值。On表示仿真網絡中重疊節點的個數。Om表示仿真網絡中重疊節點所屬的社區個數。t1為仿真網絡節點度數的密率分布指數。t2為仿真網絡社區大小的密率分布指數。混合參數μ取值范圍是[0，1]。取值越大，生成的仿真網絡社區結構越不明顯，當取值為0時，整個網絡是一個社區；當取值為1時，則生成的是一個隨機網絡。實際上，真實社會網絡大多具有一定的社區結構性，因此本實驗使用的仿真網絡數據集μ取值范圍是[0，0.8]，每次增加0.1。

Table 1 LFR benchmark network dataset表1 LFR基準網絡數據集

本文使用Lancichinetti等人在文獻[40]中提出的標準互信息（normalized mutual information，NMI）評估算法在仿真網絡數據集上的社區檢測質量。NMI可以測量兩個社區間的相似程度，NMI∈[0,1]，其值越大表明兩個社區越相似。NMI具體信息詳見式（3）。

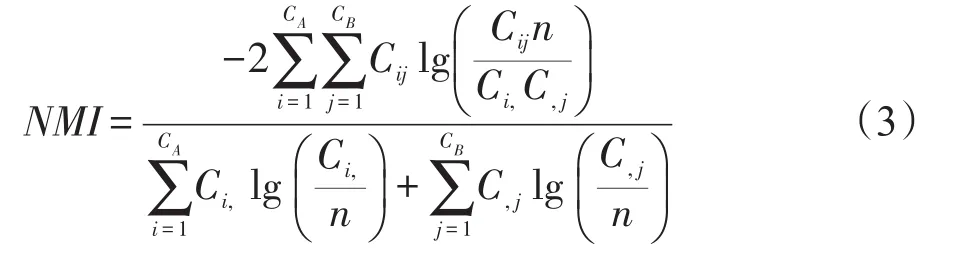
其中，A和B表示網絡的兩種劃分結果，C表示混合矩陣，其元素Cij表示劃分A中的社團i里面的節點在劃分B中的社團j里面出現的個數。CA和CB表示劃分A和劃分B中的社團的個數，Ci,表示矩陣C中第i行的元素之和，C,j表示矩陣C中第j列的元素之和，n表示網絡的節點個數。

4.1.2 真實網絡數據和評價方法

考慮到真實社會網絡和仿真網絡的拓撲結構等信息存在一定的差異性，使用5種不同規模的真實社會網絡（Karate[41]、Dolphins[42]、Football[43]、Power[44]和 CA-hepPH[45]）對社區檢測算法進行性能評價。Karate[41]是圣所迦利的空手道俱樂部的人際關系社會網絡，該網絡具有34個節點和78條邊，是一個小規模的真實社會網絡。Dolphins[42]是Lusseau等[46]在新西蘭對62只寬吻海豚的生活習性進行了長時間的觀察，發現海豚的交往呈現出特定的模式，并構造了包含62個節點的海豚社會網絡。Football[43]是美國大學秋季比賽中各足球俱樂部通過比賽關系產生的社會網絡。Power[44]是美國西部電網構成的復雜網絡。CA-hepPH[45]是一個科學家合作的較大規模的真實社會網絡，具有11 204個節點和117 649條單向邊。這些社會網絡（如表2所示）中的節點代表的是真實個體，而邊代表了個體之間的關系。它們的規模、拓撲結構等特性不同，應該能夠更好地評價社區檢測算法的性能。

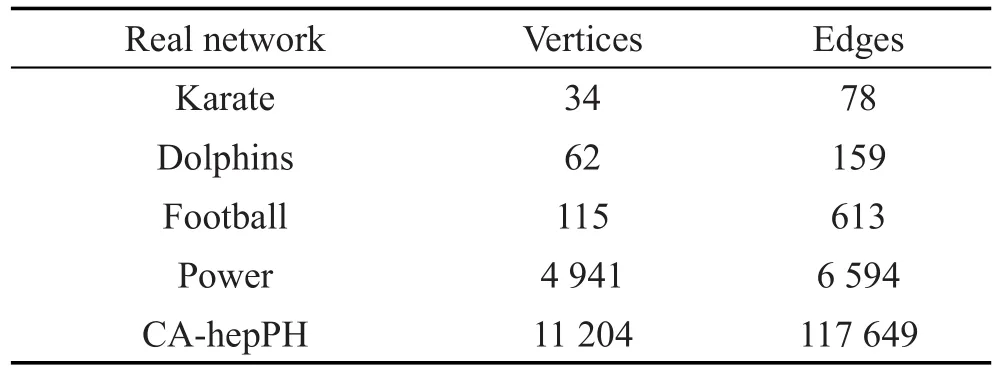
Table 2 Real social network dataset表2 真實社會網絡數據集

人們通常不了解真實社會網絡的社區結構情況，也很難有事實上的評價標準。Newman等提出的模塊度[47-49]方法得到廣泛認可并被用于評價社區檢測算法在真實社會網絡數據集上的社區檢測質量。其中，文獻[49]將問題擴展到無向無權重復雜網絡，提出一個用于檢測重疊社區的模塊度函數Qov，詳見式（4）所示。

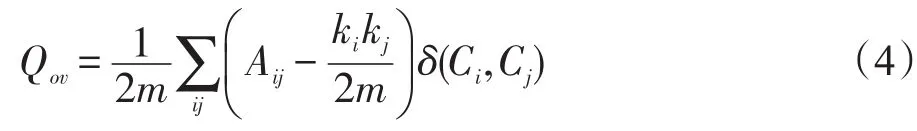
在式（4）中，m表示復雜網絡的邊數。ki、kj是節點i、j的度數。A是網絡的鄰接矩陣，如果節點i和j相鄰，則Aij=1，否則Aij=0。如果節點i和j在同一個社區，δ(Ci,Cj)=1，否則δ(Ci,Cj)=0。

4.2 算法性能

GCE算法[50]提出k-clique中的參數k為3或4時，clique的大小是比較恰當的。因此，本節對MC的長度進行了限定，分別為|MC|≥3和|MC|≥4兩種情況，并使用ALPA-S算法驗證兩種情況下的社區檢測質量。ALPA-S算法分別在S1、S2、S3和S4仿真網絡數據集對應的32個仿真網絡上運行10次，并對社區檢測結果的NMI值進行了平均計算，結果如圖3（a）～圖3（d）所示，其中圖3（a）為仿真網絡數據集S1上的結果，圖3（b）為仿真網絡數據集S2上的結果，圖3（c）為仿真網絡數據集S3上的結果，圖3（d）為仿真網絡數據集S4上的結果。

圖3表示ALPA-S算法在兩種MC長度下在仿真網絡S1(a)、S2(b)、S3(c)和S4(d)上的社區檢測質量。實驗結果表明，當μ＞0.5且|MC|≥4時，在小型仿真網絡數據集S1和S2上，ALPA-S算法沒有取得較好的社區檢測質量。而在較大的仿真網絡數據集S3上，ALPA-S算法在兩種長度的MC上均取得了較好的社區檢測質量。但在S4數據集上，當|MC|≥4時，ALPA-S算法的社區檢測質量明顯劣于|MC|≥3時。實際上，當|MC|≥4時，僅僅包含3個節點的小型社區無法被正確檢測，而文獻[25]證實過一個真實社會網絡的社區可能只包含3個節點。綜合考慮，選擇|MC|≥3作為ALPA-S算法和ALPA-A算法初始化時極大團長度的限定條件。

另外，ALPA-S和ALPA-A在仿真網絡中檢測的極大團個數即是兩種算法初始化時產生的標簽數，為了證明這種方法極大地降低了算法中的冗余標簽數以及減少了算法更新時標簽選擇的代價，現以ALPA-S算法為例，使用表1中較大的仿真網絡數據集S3和S4對應的16個仿真網絡作為實驗數據集驗證ALPA-S算法中產生的標簽數以及標簽節點比，實驗結果如圖4中的（a）和（b）所示。其中，標簽節點比如式（5）所示。在式（5）中，Cn表示仿真網絡在ALPAS算法初始化時產生的標簽數c與該仿真網絡節點數n的比值，即標簽節點比。

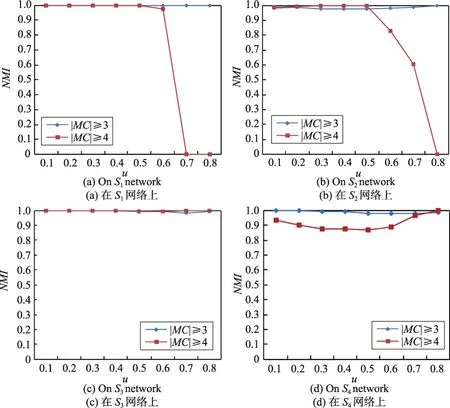
Fig.3 Community detection result ofALPA-S algorithm in both MC lengths圖3 ALPA-S算法在兩種MC長度下的社區檢測質量

在圖4的（a）和（b）中，ALPA-S算法在每個仿真網絡數據集上進行了10次實驗，產生的標簽數量略有差異。對10次實驗產生的極大團數求平均值。從圖4（a）、（b）中可以看出，ALPA-S算法在16個仿真網絡上產生的標簽節點比（label-node ratio）均小于10%，這極大降低了ALPA-S算法迭代時標簽選擇的風險，算法結果相對更穩定。另外，這里應該被提及的是ALPA-S算法和ALPA-A算法在尋找極大團時，當有兩個或更多個影響力相同的鄰接節點同時符合條件加入一個極大團時，算法隨機選擇其中一個節點。這種隨機選擇可能導致社區劃分質量的差異。但是，通過實驗結果分析得知，這種隨機選擇引起的社區劃分質量不穩定性誤差范圍在0.1%左右。可見，這種隨機選擇并未引起兩種算法社區檢測質量的較大不穩定性。被隨機選擇加入極大團忽略的節點可能最終都沒有被加入到任何一個極大團中，但在后續的標簽更新過程中，其仍然會和與它有最多關聯關系的極大團中的節點擁有同一個標簽，并進而屬于同一個社區。因此，構建極大團時的節點隨機性選擇問題對兩種算法社區檢測質量的影響較小。

使用表1的S5數據集驗證ALPA-S和ALPA-A兩種算法在具有不同重疊社區數的仿真網絡中的社區檢測質量，結果如圖5所示。從圖5可知，當Om=0時，即仿真網絡中沒有重疊社區時，兩種算法均取得了較好的社區檢測質量。說明兩種算法均適合于具有非重疊社區結構的復雜網絡。隨著網絡中節點所屬的重疊社區數目的增加，兩種算法均保持著良好的社區檢測質量，說明兩種算法亦均適合于節點屬于多個重疊社區的復雜網絡上的社區檢測。但是從圖5顯示的結果可以看出，在5種仿真網絡數據集上，同步算法ALPA-S的社區檢測質量略優于異步算法ALPA-A。

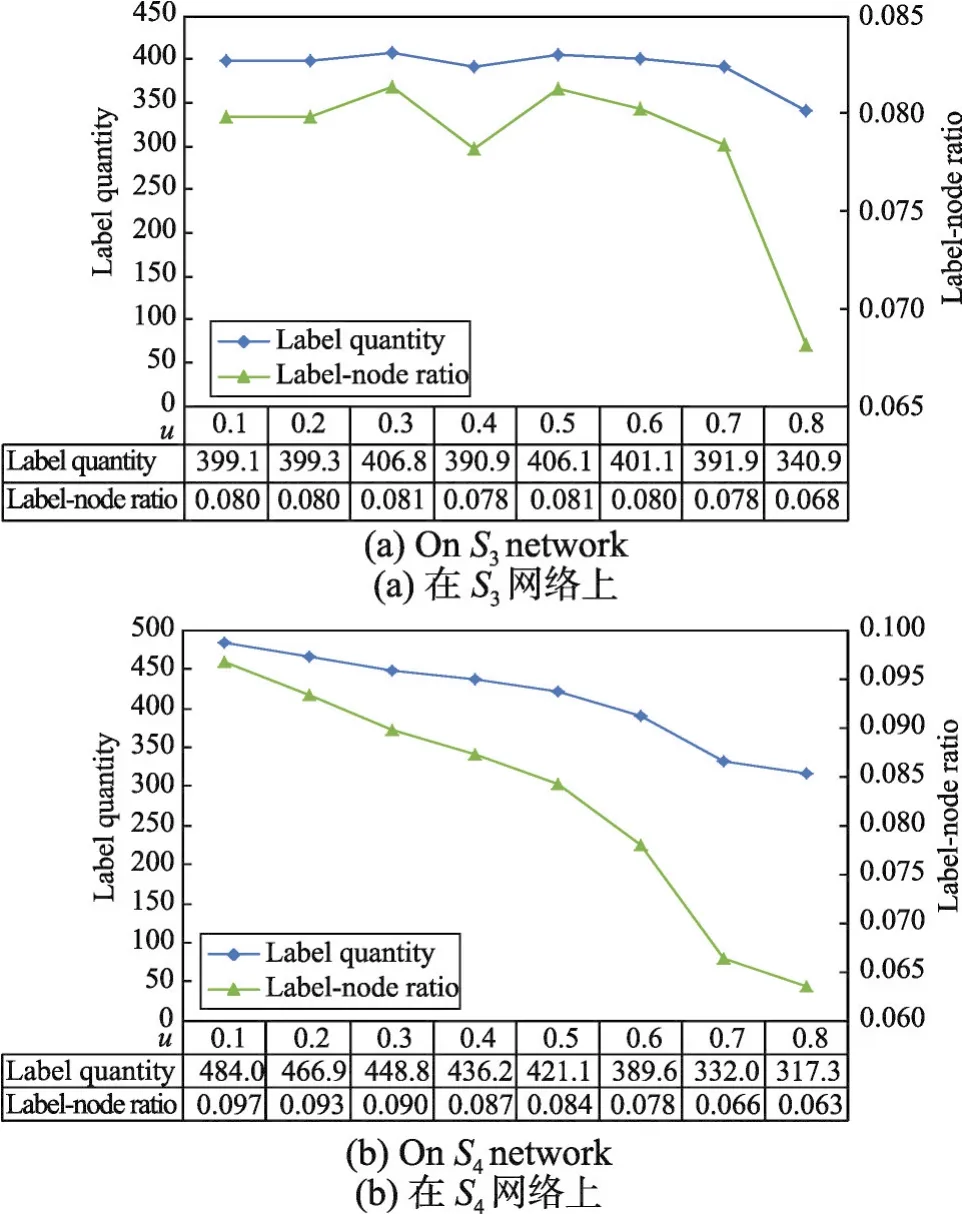
Fig.4 Number of labels and label-node ratio ofALPA-S algorithm on artificial networks圖4 ALPA-S算法在仿真網絡上產生的標簽數及標簽節點比

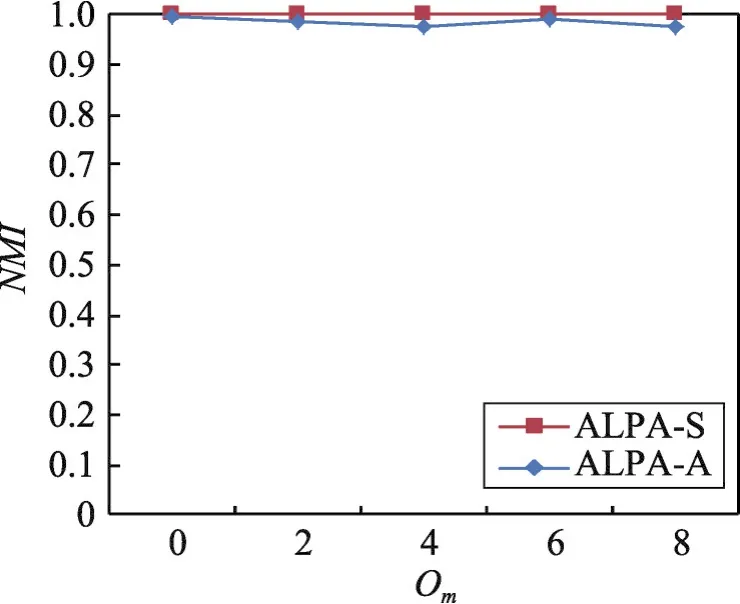
Fig.5 Result of community detection of two kinds of algorithms on artificial networks containing different number of overlapping community圖5 兩種算法在具有不同重疊社區數的仿真網絡上的社區檢測質量

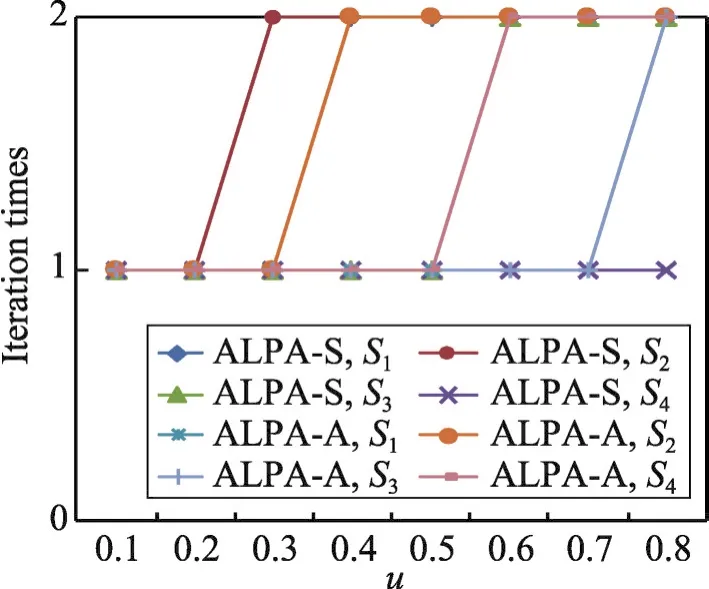
Fig.6 Iteration number of two kinds of algorithms on 32 artificial networks圖6 兩種算法在32個仿真網絡上的迭代次數

ALPA-S和ALPA-A兩種算法均提出極大團MC是社區的核心結構，社區內的其他節點應該圍繞在極大團的周圍。使用實驗中的迭代次數來進行驗證，結果如圖6所示。圖6顯示了同步算法ALPA-S和異步算法ALPA-A分別在32個仿真網絡上進行實驗算法收斂時需要的迭代次數。結果表明兩種算法在32個仿真網絡上收斂時所需要的迭代次數均為1～2次，說明極大團MC是社區的核心結構，其余節點在MC的周圍且通過1～2步即可到達MC中的節點。也進一步說明了兩種算法的迭代計算代價是比較小的。另外，通過在32個仿真網絡上的迭代次數計算可知，這兩種算法都極容易收斂。其中，ALPA-S在32個仿真網絡上的平均迭代次數是1.438，而ALPAA則是1.375。這也進一步說明同步算法需要更多的迭代次數才能夠使算法收斂，而異步算法的收斂速度較快。

4.3 和其他算法的對比

（1）仿真網絡上的實驗

使用32個仿真網絡數據集（如表1的S1、S2、S3和S4所示）對比ALPA-S算法、ALPA-A算法和其他幾個經典算法如LPA算法、COPRA算法、DEMON（democratic estimate of the modular organization of a network）算法[27]和GCE（greedy clique expansion）算法在稀疏和稠密復雜網絡上的社區檢測性能。結果分別如圖7中的（a）～（d）所示。

圖7展示了相關算法在4種類型32個仿真網絡S1、S2、S3和S4上的社區檢測質量，分別如圖7中的（a）～（d）所示。從圖7可以得出如下結論：

①LPA算法、COPRA算法、GCE算法和ALPA-A算法在不同類型的復雜網絡上的社區檢測質量不穩定；

②ALPA-S算法和DEMON算法在混合參數μ值逐漸增加，社區結構逐漸不清晰的情況下，無論在稀疏還是稠密復雜網絡中均呈現了較好的社區檢測質量。

（2）真實網絡上的實驗

在5種真實社會網絡數據集上繼續驗證所提算法的社區檢測質量，并使用模塊度函數Qov作為評價標準，結果如圖8所示。從圖8可以得出如下一些結論：

①ALPA-S算法在5種真實社會網絡上的社區檢測質量總體好于其他5種算法;

②ALPA-A算法在不同社會網絡上的社區檢測質量仍然表現出了一定的不穩定性;

③在仿真網絡實驗中一直表現較好的DEMON算法，在真實社會網絡中的社區檢測質量卻明顯表現不佳。

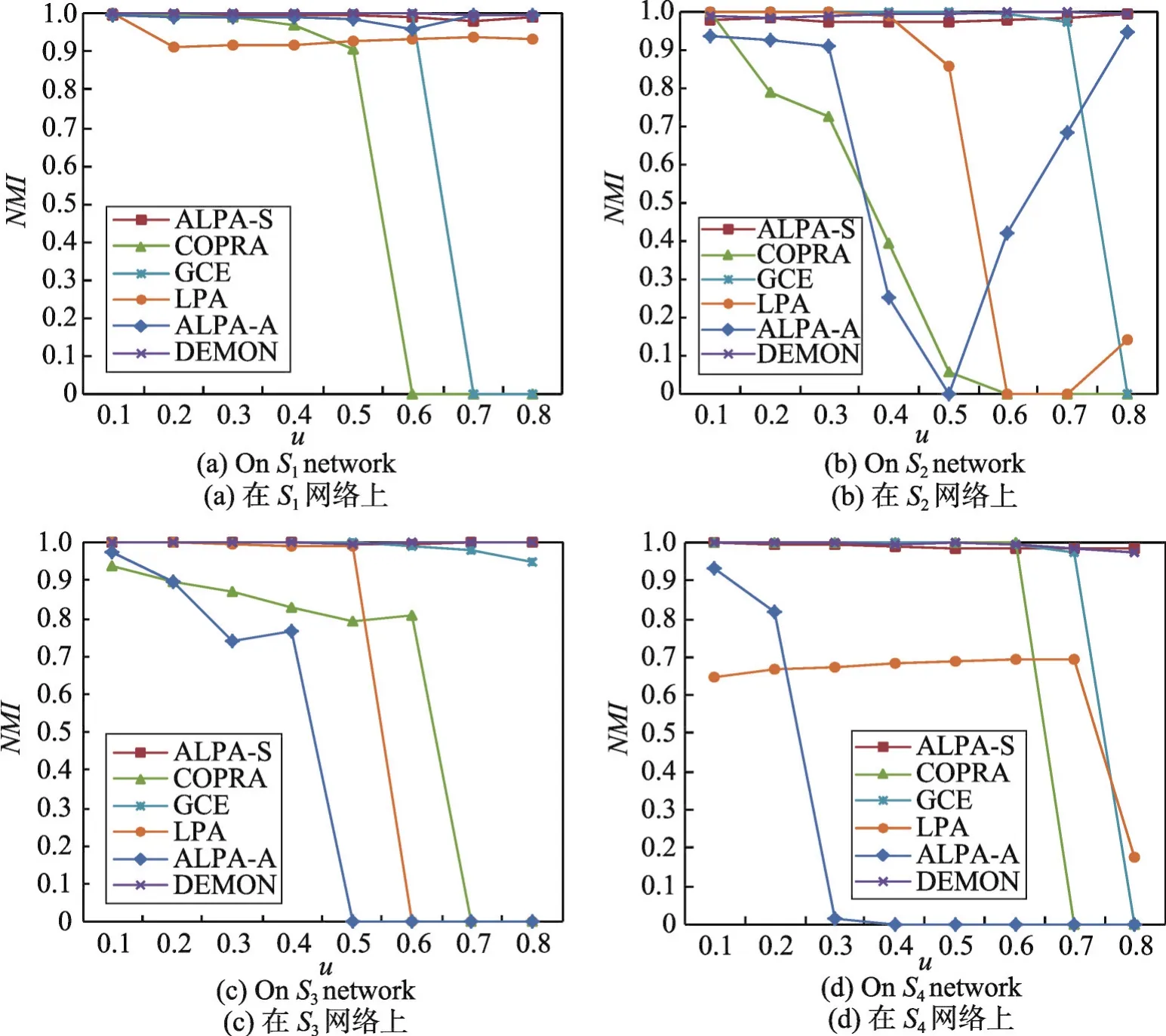
Fig.7 Result of community detection of related algorithms on 4 kinds of benchmark networks圖7 相關算法在4種類型仿真網絡上的社區檢測質量

同時，在5種真實社會網絡上檢驗算法在初始化時產生的標簽節點比及算法的迭代次數，以便進一步驗證本文提出算法的性能，結果分別如圖9和圖10所示。從圖9和圖10中可以看出，不同真實復雜網絡被ALPA-S算法初始化后產生的標簽節點比差異較大。其中，電力網絡Power初始化后的標簽節點比僅為4.37%，而迭代次數卻多達10次和7次，這和仿真網絡上的實驗結果有較大的不同。因此，對使用ALPA-S算法通過最后一次迭代才能擁有標簽的節點所在的社區之一進行了可視化分析。選中的社區包含100個節點，為了繪圖方便，對該社區中的100個節點重新映射編號，可視化結果如圖11所示。從圖11可以看出該社區呈現近似樹狀的拓撲結構特征，并且其僅包含1個極大團{26，67，71}，如圖11紅色部分所示，其余節點均圍繞在該極大團的周圍。從這些結果可知，Power中極大團數量較少，因此初始化時其獲得的標簽數量亦較少，這解釋了圖9中Power網絡具有較小的標簽節點比以及需要較多迭代次數的根源。另外，從圖8可知，ALPA-A算法在Power上的表現好于其他5種算法，這也許可以說明當社區中的核心結構較少時，異步算法能夠更快收斂的同時，亦能取得更好的社區檢測質量。

綜上所述，通過仿真網絡和真實網絡上的實驗表明，異步算法ALPA-A能夠更快地使算法收斂，其在社區核心結構較少的社會網絡中能夠取得較好的社區檢測質量，但是在不同類型復雜網絡中的社區檢測質量仍然不夠穩定。而同步算法ALPA-S無論在稀疏或稠密、社區結構明顯與否以及在各種不同類型的真實社會網絡中的社區檢測質量均優于其他社區檢測算法，體現了其具有較好的自適應性、穩定性和健壯性。

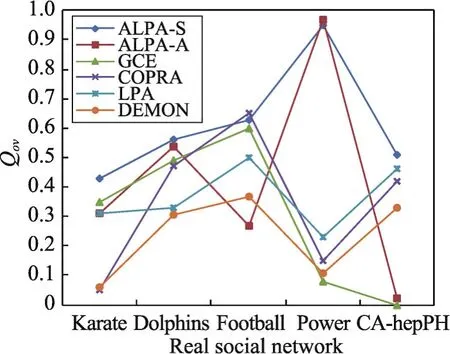
Fig.8 Modularity of community detection of related algorithms on 5 real social networks圖8 相關算法在5種真實社會網絡上的社區檢測模塊度

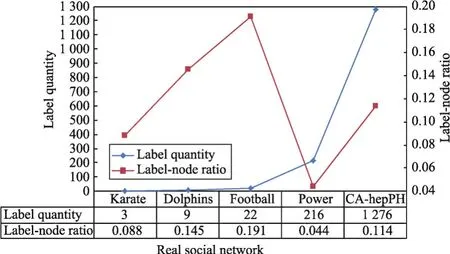
Fig.9 Number of labels and label-node ratio of ALPA-S algorithm on real social networks圖9 ALPA-S算法在真實網絡上的標簽數及標簽節點比

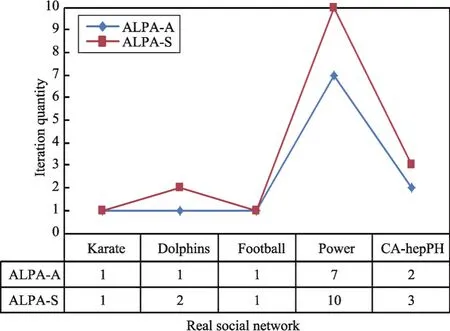
Fig.10 Iteration number ofALPA-S algorithm on real social networks圖10 ALPA-S算法在真實社會網絡上的迭代次數

5 結束語

由于依靠網絡拓撲結構信息對社會網絡社區結構進行挖掘具有模型簡單、計算效率高和易于應用等特點，本文提出了單純依靠社會網絡拓撲結構信息的同步自適應標簽傳播算法ALPA-S和異步自適應標簽傳播算法ALPA-A檢測復雜網絡中的社區結構。通過對兩種算法的性能分析以及和其他經典算法的對比，表明同步算法ALPA-S更適合于檢測不同類型社會網絡中的重疊社區結構和非重疊社區結構。另外，不需要參數控制的ALPA-S算法能夠根據復雜網絡的拓撲結構信息自動調整初始化時極大團中節點的個數以及根據節點標簽個數自動調整閾值并剔除無意義的標簽，具有良好的自適應性。因此其能更好地適應沒有先驗知識的真實社會網絡。另外，本文提出的算法證實了一個社會現象：一個社區結構（群體）至少包含一個影響力較大的核心群體（極大團MC），社區影響力較弱的群體則圍繞在影響力較大的核心群體的周圍。下一步，考慮將ALPA-S算法進行并行實現，從而可以更好地解決大規模以及超大規模社會網絡中的社區檢測問題。

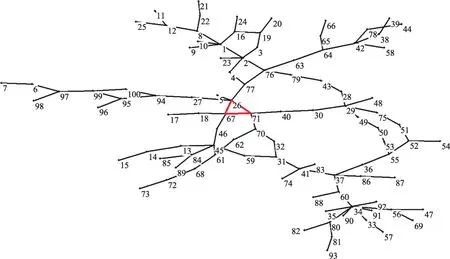
Fig.11 Graph of visualization result of a community in Power social network圖11 Power中一個社區的可視化結果圖