基于GM(1,1)和人工蜂群的配電測試系統狀態估計

符金偉， 關石磊， 左思然， 范聞博， 王中宇

(1. 中國電力科學研究院配電研究所，北京 100085; 2. 北京航空航天大學儀器科學與光電工程學院，北京 100191)

0 引 言

配電測試系統狀態估計方法是一種利用測試系統中量測數據的相關性和冗余度，對運行參數和運行狀態進行預測和估計，為其他電力控制設備提供完整、可靠、高精度實時數據的方法[1]。

常用的狀態估計方法有加權最小二乘法、等效功率變換法、基于支路估計法等。加權最小二乘法將量測值與其估計值之差的平方和作為目標函數，具有模型簡單、收斂性好等優點，但是該方法也存在運算量大、抗差能力弱等問題[2]。等效功率變換法將支路功率、電壓幅值和電流幅值轉換為支路兩端等效功率，該方法具有計算速度快、內存占用少的優點，但是不易處理注入型的量測量[3]。支路估計法將整個配電網的狀態估計問題分解為與對應支路數相等的狀態估計子問題。該方法與潮流計算的前推回代相類似，計算速度快，但是根節點電壓的正確性對計算結果的影響很大，一般只用于輻射網[4-5]。

人工蜂群算法由Karaboga提出，其目的是解決多變量函數的優化問題。該算法利用雇傭蜂、偵察蜂和跟隨蜂3種具有不同功能的蜂群采集并尋找最優蜜源[6]。在蜜蜂個體局部尋優的基礎上，通過比較適應度函數確定全局最優解[7]。人工蜂群算法的魯棒性強并且具有較好的尋優質量，因此被廣泛應用于配電網網絡重構、求解電力系統最優潮流模型和配電網狀態估計等方面。但是，人工蜂群算法運用于狀態估計時，存在節點狀態估計準確度不穩定，容易陷入局部最優解等問題。分析其主要原因在于，量測數據在測量和傳送過程中存在著偶然故障和隨機干擾，因此配電測試系統的量測數據中存在著不良數據，這些不良數據造成了狀態估計準確度的惡化。

GM(1,1)模型是灰色理論最基本的一種預測模型，它通過原始量測數據的預處理和灰色模型的建立，對數據序列進行外推[8]。對原始量測序列進行灰色生成，能夠使非負序列或擺動序列轉化為非減序列，從而削弱量測數據的隨機性，突出量測數據的內在規律性，有效判別序列中是否存在不良數據。

本文提出基于GM(1,1)的不良數據修正方法，減少不良數據對狀態估計誤差的影響。在現有的人工蜂群算法基礎上采用Metropolis準則[9]進行迭代終止判定，從而避免陷入局部最優解，提升算法的全局搜索能力。

1 狀態估計模型

1.1 目標函數

配電測試系統實時量測是對裝設在饋線上的測量裝置進行實時收集，包括節點電壓幅值、支路有功功率和無功功率、節點注入有功功率和無功功率等。量測量z可以表示為

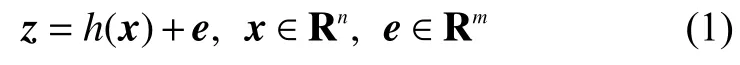
式中：h(x)——量測函數；

e——量測過程中引入的隨機誤差；

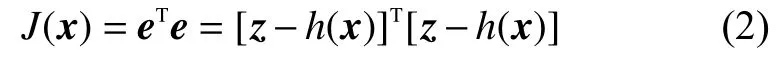
當J(x)達到最小值時，得到加權最小二乘法的估計結果。

1.2 等式約束和不等式約束

對配電測試系統進行狀態估計時，需要滿足等式約束和不等式約束條件[10]。等式約束條件基于基爾霍夫第一定律，目標函數的求解值必須滿足一組約束條件。

不等式約束條件有負荷有功、負荷無功、節點電壓約束，可表示為

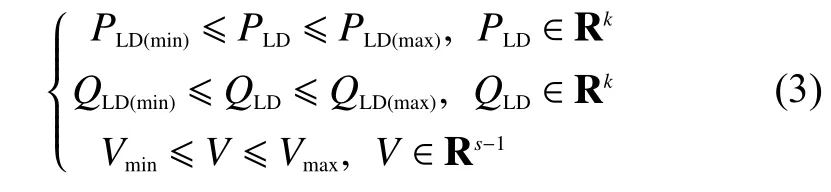
式中：PLD——負荷有功功率，W；

QLD——負荷無功功率，W；

V——除起點外的所有節點電壓的幅值，V；

k——負荷節點數；

s——所有節點數。

2 不良數據修正

通常，配電測試系統量測數據分為有效量測數據和量測噪聲兩部分。由于粗差的出現，實際噪聲分布與假設的量測噪聲分布模型存在偏移，因此不良數據是影響狀態估計結果準確性的關鍵因素[11]。傳統的不良數據辨識方法有標準殘差法、零殘差法和非二次準則法等，但是這些方法均無法消除殘差污染和殘差淹沒，進一步會造成不良數據的誤判和漏檢[12]。為了克服殘差污染和殘差淹沒現象，引入GM(1,1)模型實現對不良數據的修正。

以根節點電壓幅值V為例，選擇一定的時間窗口，讀取量測值。令多組原始量測值按從小到大排序，其序列記為V(0)。對序列V(0)做累加生成，得到測量值累加數列V(1)：

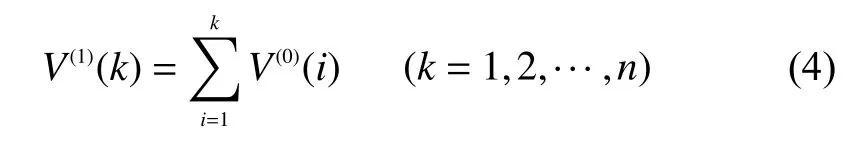
式(4)的累加曲線可以用一個折線來包絡，包絡線的下界的折線方程為

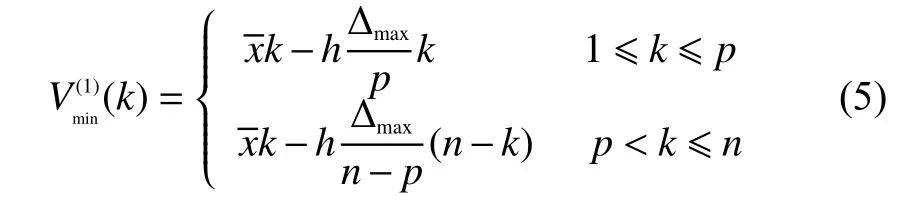
其中h一般取3.75。

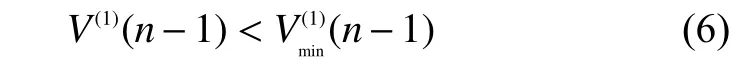
對于量測值序列如果滿足式(6)，則認定量測值中有不良數據，V(0)(n-1)和V(0)(n)可剔除；否則，最大量測值是否為不良數據無法判定。因此需要為數據V(1)建立GM(1,1)模型獲得一個預測值V(1)(n+1)。GM(1,1)灰色微分方程為

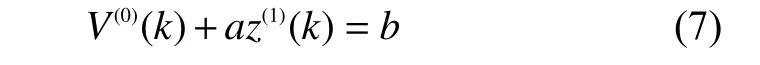
式中：a——GM(1,1)的發展系數；

b——GM(1,1)的灰作用量。

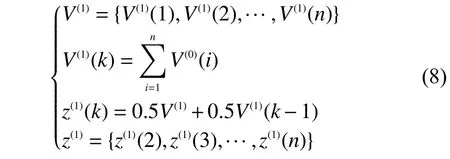
式中：z(1)——V(1)的均值序列；

V(1)——V(0)的一次累加序列。

通過求解灰色微分方程可以得到預測值(1)(n+1)，表達式為

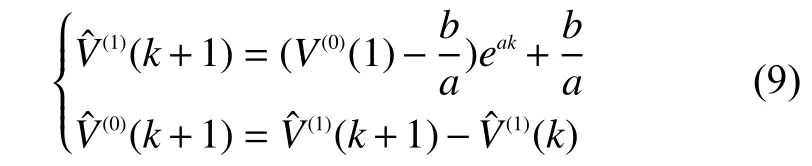
其中k=1,2,···,n。

為了保證每個節點量測數據的個數不變，采用線性插值法對不良數據進行修正，即不良數據的修正值采用其前后兩次測量值的均值。

3 配電測試系統狀態估計

有將負荷有功功率和無功功率作為狀態變量：

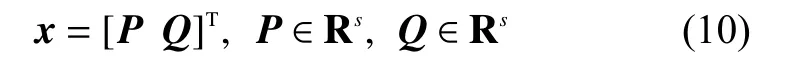
式中：P——負荷有功功率，W；

Q——負荷無功功率，W。

則量測函數表達式為

式中：V——節點電壓幅值的量測值，V；

I——節點電流幅值的量測值，A。

配電測試系統狀態估計就是對1.1節中提出的目標函數進行優化求解。采用改進的人工蜂群算法對其進行求解，步驟如下：

1)種群初始化

輸入初始參數，包括蜂群的規模M、雇傭蜂的規模S和最大迭代次數MAX，并將局部搜索限度trail置零。

隨機生成S個狀態向量，則產生可行解的公式為

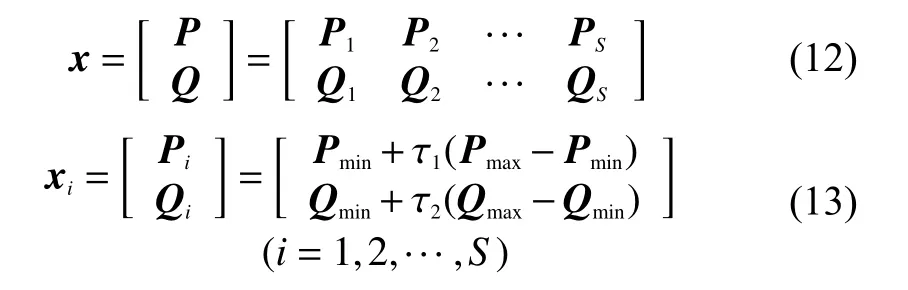
其中τ1、τ2為0～1之間的隨機數。

將蜜源設置為目標函數J(x)，計算各個狀態向量對蜜源的適應度fit(x)。

2)雇傭蜂階段

雇傭蜂在蜜源的鄰域進行隨機搜索，表達式為

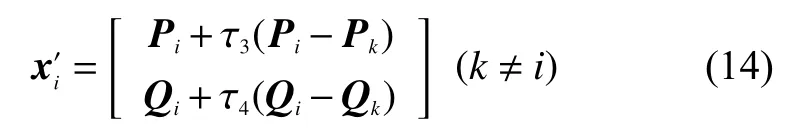
其中τ3、τ4為0～1之間的隨機數。

計算當前狀態量對蜜源的適應度fit(xi′)，比較fit(xi)與fit(xi′)的大小。若fit(xi′)＞fit(xi)則狀態量更新為xi′；否則保持原狀態量xi不變。同時將trail(i)加1，若trail(i)=trail則雇傭蜂變為偵察蜂并放棄該解，進入步驟4)；否則執行步驟3)。

3)跟隨蜂階段

跟隨蜂以一定的概率選擇狀態量，概率計算的表達式為

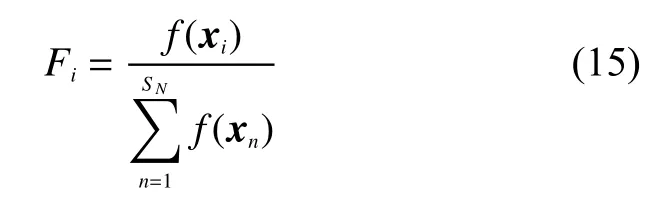
在其附近進行隨機搜索，搜索方式與步驟2)中的雇傭蜂相同。若fit(xi′)＞fit(xi)則狀態量更新為xi′，跟隨蜂代替雇傭蜂的位置；否則保持xi不變。

4)偵察蜂階段

令trail(i)=0，偵察蜂根據式(14)隨機生成新的狀態量xi′。當fit(xi′)＞fit(xi)時更新狀態量為xi′，偵察蜂變為雇傭蜂；否則保持不變。

5)迭代終止判定

每一次迭代后，若最優解的適應度函數增大，那么就接受它；否則按照下式來判斷是否接受：

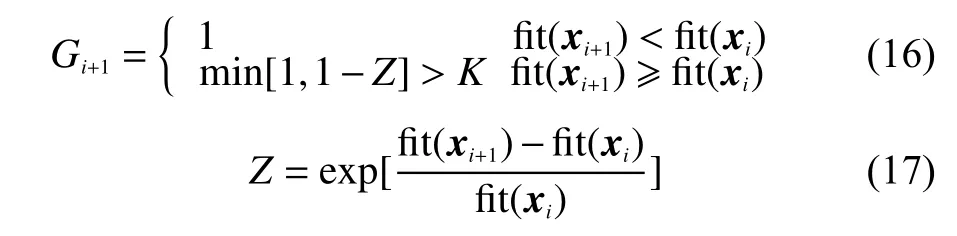
式中：K——0～1之間的判定閾值，通常取0.5；

G(xi+1)——狀態xi+1下的接受概率。

xi+1可以表示為

其中α為溫度冷卻系數。

令總循環次數加1，判斷是否達到迭代終止條件，如果是則終止迭代并輸出最優解；否則重新返回步驟2)。

6)記錄當前的最優解。

4 實驗分析

為了對本文提出的方法進行驗證，采用由中國電力科學研究院搭建的33節點配電測試系統開展實驗，其接線圖如圖1所示。分別在節點4、8、12、15、21、23、28和31上配置配電自動化終端和分布式電源。

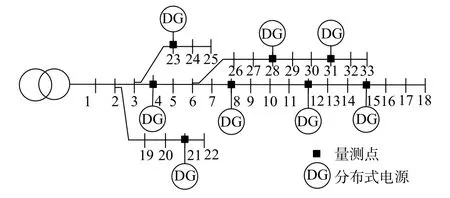
圖1 33節點配電測試系統接線圖

采用GM(1,1)方法分別對8個節點的電壓幅值和電流幅值進行不良數據檢測，得到節點4中第18次量測數據、節點12中第11次量測數據以及節點28中第6次量測數據為不良數據，如圖2和圖3中的紅色叉號所示。

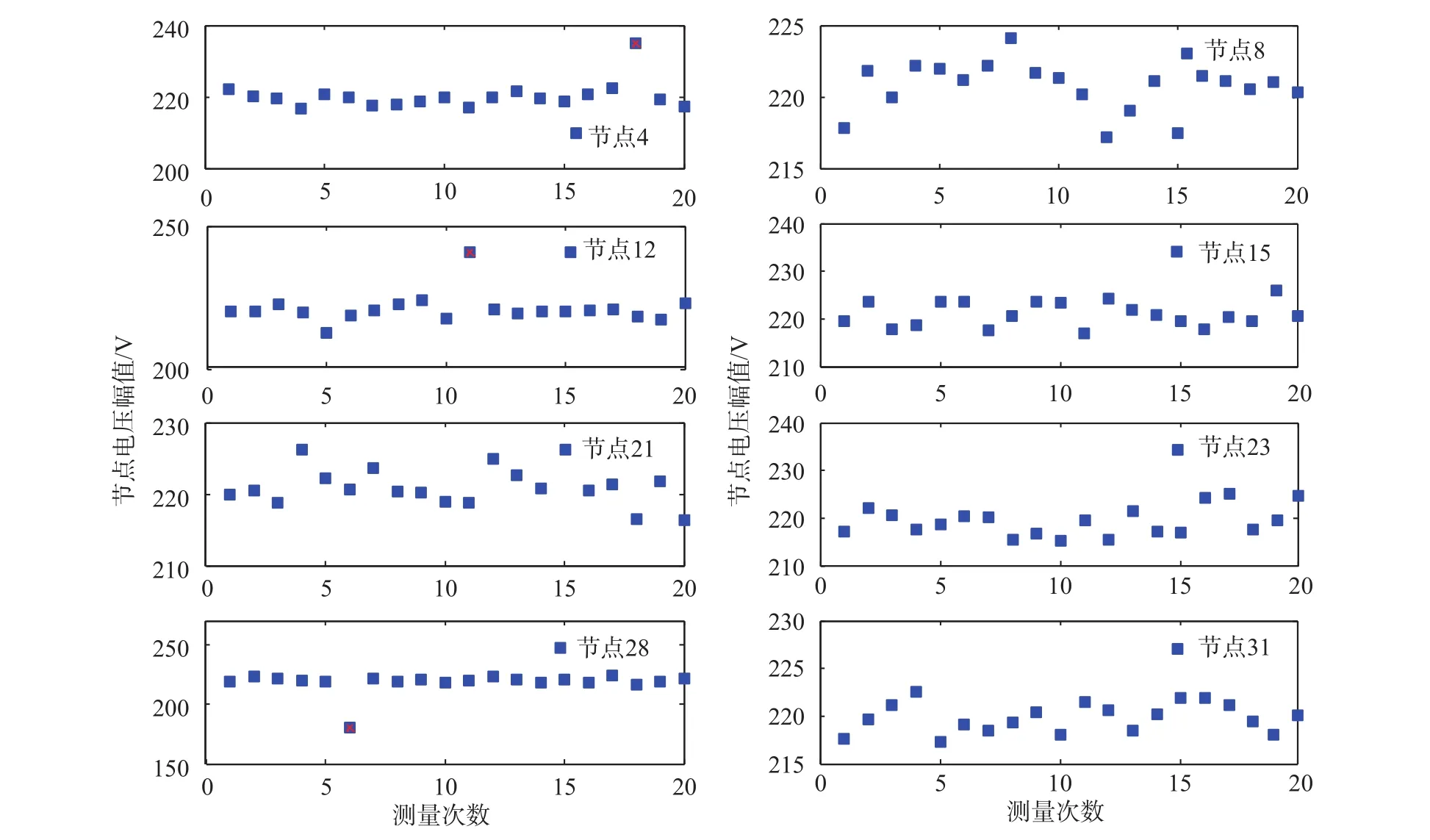
圖2 節點電壓幅值

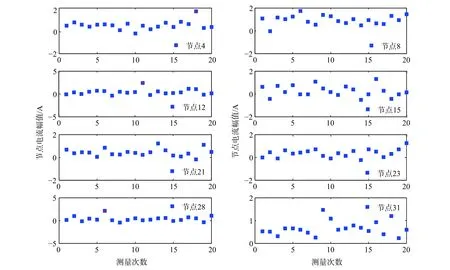
圖3 節點電流幅值

采用線性插值的方法對檢測到的不良數據進行修正，即計算出不良數據的前后各一次量測值的平均值，將其作為節點當次量測的修正值[13]。各節點的不良數據的修正結果如表1所示。

表1 不良數據修正

完成不良數據的檢測與修正后，采用改進的人工蜂群算法進行配電網狀態估計。設定蜂群的規模為50，雇傭蜂的規模為25，局部搜索限度為6，最大迭代次數為300。設定隨機數τ1和τ2的值為0.5，隨機數τ3和τ4的值為0.3，溫度冷卻系數α的值為1.5。同時，根據原始量測數據，分別采用加權最小二乘法和人工蜂群算法進行狀態估計。表2和表3分別表示采用不同方法下有功功率和無功功率的估計結果。

對8個節點的負荷有功功率和無功功率進行估計時，不同方法的估計誤差絕對值如圖4和圖5所示。通過各節點估計誤差絕對值的比較發現，加權最小二乘法的誤差最大，其次是人工蜂群算法，而本文方法的誤差最小。另外，對存在不良數據的節點4、12和28進行分析后可以發現，相對于加權最小二乘法和人工蜂群算法，本文方法的估計誤差絕對值的波動范圍最小。

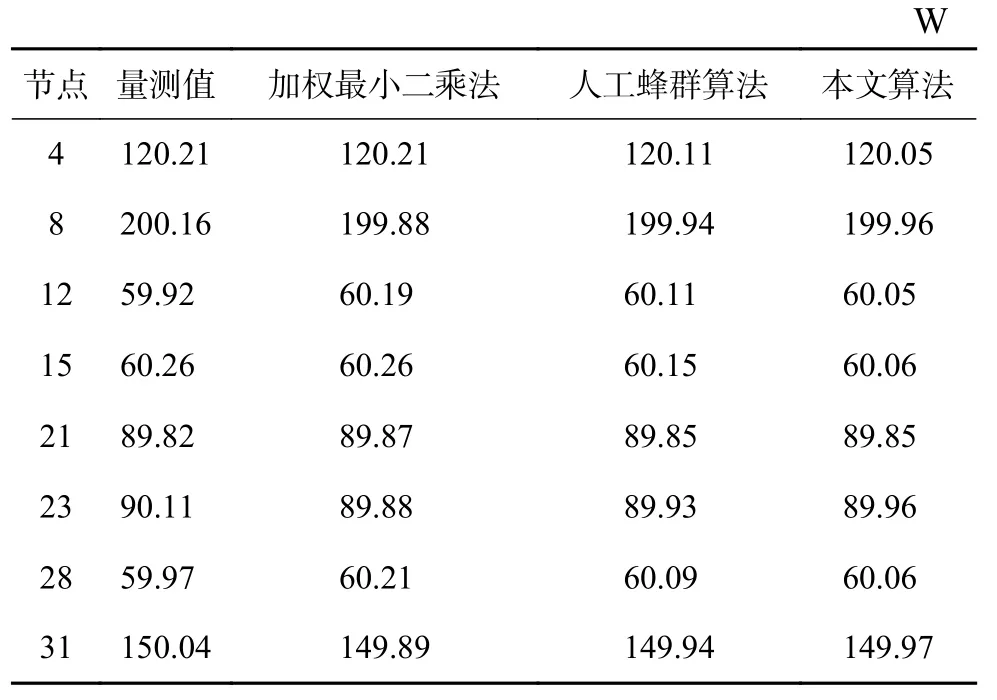
表2 負荷有功功率估計結果比較

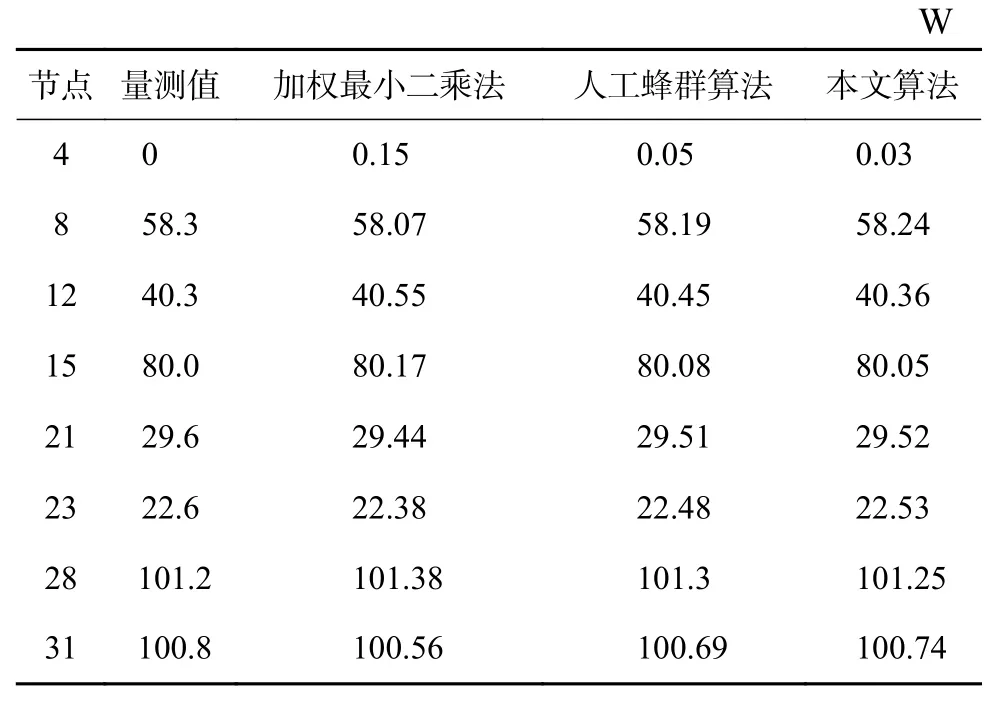
表3 負荷無功功率估計結果比較

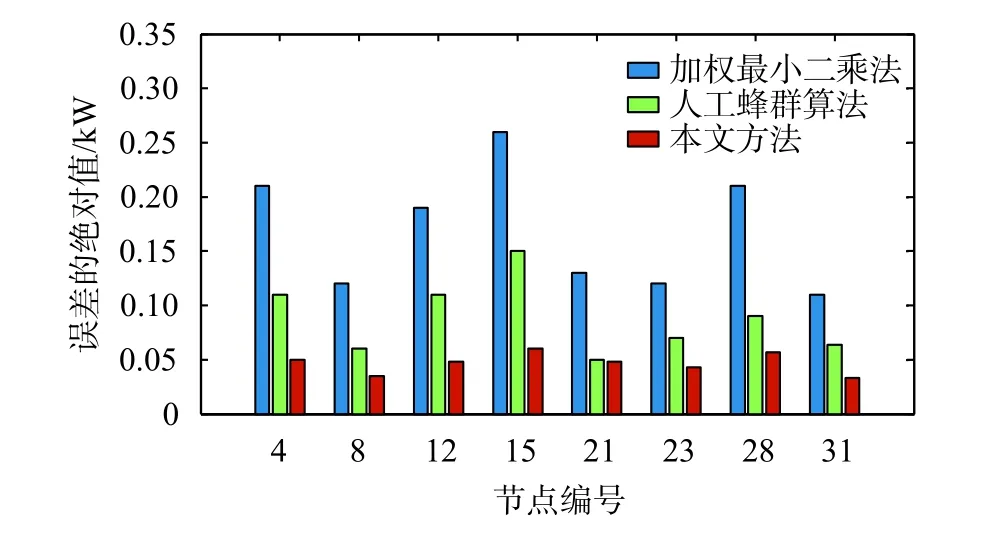
圖4 有功功率估計誤差絕對值比較

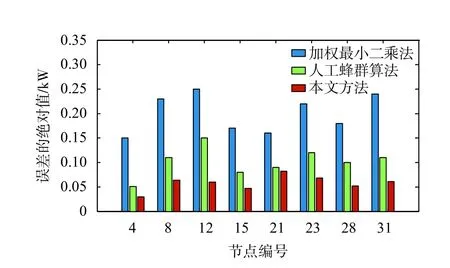
圖5 無功功率估計誤差絕對值比較

同時，采用不同方法對選取的8個節點重復進行15次狀態估計，記錄運行時間，得到8節點狀態估計的平均運行時間如表4所示。

表4 不同方法的平均運行時間比較

由表可知，加權最小二乘法的復雜度低，因此該算法的平均運行時間最短；人工蜂群算法在存在不良數據時對全局最優值的搜索效率不高，平均運行時間最長。本文方法的平均運行時間與加權最小二乘法的相接近，同時比人工蜂群算法減少了46%。

為了對這3種狀態估計方法的誤差進行比較，定義平均絕對誤差MAE和節點最大相對誤差NMRE：

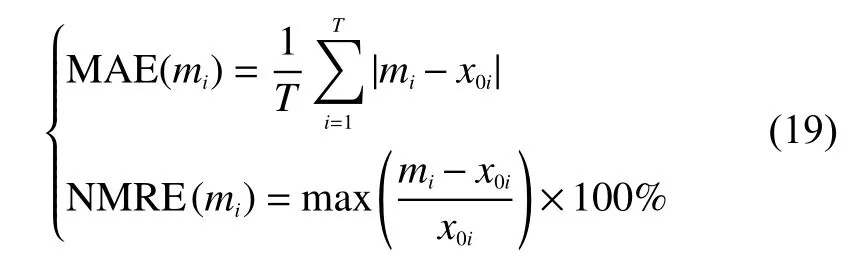
式中：mi——i時刻狀態量的估計值；

xi——狀態量的真值；

T——節點數目。

根據式(19)計算出不同方法估計有功功率和無功功率時的MAE和NMRE，結果如表5所示。

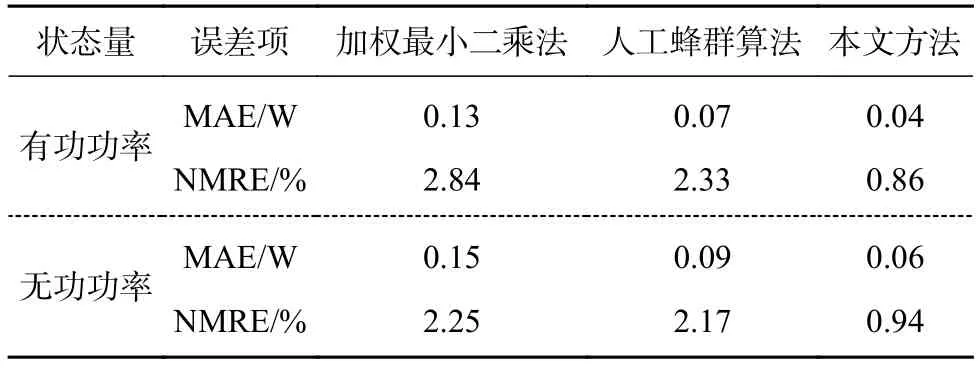
表5 不同方法估計誤差比較

由表可知，本文方法估計的有功功率MAE比加權最小二乘算法和人工蜂群算法的相應結果分別減少了大約69%和43%，NMRE分別減少了70%和63%；對于無功功率，本文方法比加權最小二乘算法和人工蜂群算法的MAE結果分別減少了大約60%和33%，NMRE分別減少了58%和57%；這說明本文方法對于每一節點的狀態估計誤差都明顯小于加權最小二乘法和人工蜂群算法，驗證了本文方法的有效性。

5 結束語

1)本文提出了一種基于灰色累加生成和人工蜂群算法的配電測試系統狀態估計方法。通過建立灰色微分方程求解序列預測值來判斷序列中是否存在不良數據，能夠解決傳統方法中存在的殘差污染和殘差淹沒問題。

2)研究了人工蜂群算法的節點狀態估計準確度不穩定、容易陷入局部最優解等問題。首先采用線性線性插值的方法對不良數據進行修正，其次建立迭代終止判定條件，提高算法的全局最優搜索能力。在存在不良數據的條件下，本文方法比人工蜂群算法的估計精度更高，運行時間更短。

3)本文對不良數據的修正采用了線性插值的方法，當量測數據的采樣頻率較低時狀態估計準確度會受到影響。因此可以作為下一步的研究方向。