基于主動視覺的手眼系統(tǒng)自標(biāo)定方法

邱曉榮， 劉全勝， 趙 吉

(1. 馬來西亞管理科學(xué)大學(xué)信息科學(xué)與工程學(xué)院，雪蘭莪 莎阿南 40100;2. 無錫職業(yè)技術(shù)學(xué)院物聯(lián)網(wǎng)技術(shù)學(xué)院，江蘇 無錫 214121; 3. 江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院，江蘇 無錫 214122)

0 引 言

視覺測量與控制作為機(jī)器人智能化最重要的實(shí)現(xiàn)方式之一，可以大幅提高機(jī)器人的效率和精度，目前在工業(yè)生產(chǎn)中有著非常廣泛的應(yīng)用。機(jī)器人在生產(chǎn)操作時，需要知道目標(biāo)物體相對于機(jī)械手末端執(zhí)行器的位置，這可以通過手眼系統(tǒng)的自標(biāo)定來獲取，獲取的關(guān)鍵在于確定機(jī)械手末端坐標(biāo)系與攝像機(jī)坐標(biāo)系之間的相對位置關(guān)系[1-3]。常見的手眼系統(tǒng)一般可以分為固定視點(diǎn)系統(tǒng)和非固定視點(diǎn)系統(tǒng)2種。非固定視點(diǎn)系統(tǒng)中，攝像機(jī)被固定在機(jī)器人機(jī)械手末端，隨末端執(zhí)行器一起移動，可實(shí)時觀測到攝像機(jī)視野中的工件圖像。

為了實(shí)現(xiàn)非固定視點(diǎn)系統(tǒng)的自標(biāo)定，目前常用的方法是在不使用標(biāo)定參照物的基礎(chǔ)上，精確控制攝像機(jī)做線性無關(guān)的平移運(yùn)動和旋轉(zhuǎn)運(yùn)動，只需依據(jù)場景中若干特征點(diǎn)，即可線性求解手眼系統(tǒng)中的攝像機(jī)內(nèi)參矩陣、手眼關(guān)系、特征點(diǎn)目標(biāo)深度等信息。楊廣林等[4]提出依據(jù)2個特征點(diǎn)，利用2次平移運(yùn)動和1次旋轉(zhuǎn)運(yùn)動，可線性求解手眼關(guān)系的平移向量和特征點(diǎn)目標(biāo)深度。許海霞等[5]提出只需1個特征點(diǎn)，利用5次以上平移運(yùn)動和2次以上旋轉(zhuǎn)運(yùn)動，可實(shí)現(xiàn)自標(biāo)定。孔令富等[6]提出利用4次純平移運(yùn)動可以計算手眼關(guān)系的旋轉(zhuǎn)矩陣，繼而實(shí)現(xiàn)特征點(diǎn)目標(biāo)深度實(shí)時估計。曲學(xué)軍等[7]提出基于平行直線束圖像序列，利用消隱點(diǎn)標(biāo)定攝像機(jī)的焦距和外參數(shù)。陳天飛等[8]通過多次平移運(yùn)動，同時結(jié)合四參數(shù)平面模型，分別標(biāo)定光平面法向量和目標(biāo)深度信息。張黎爍等[9]提出僅需2個特征點(diǎn)，通過控制攝像機(jī)做4次線性無關(guān)的平移運(yùn)動和2次旋轉(zhuǎn)運(yùn)動，即可實(shí)現(xiàn)手眼系統(tǒng)的標(biāo)定。何佳唯等[10]結(jié)合標(biāo)定板設(shè)計了一種手眼關(guān)系混合標(biāo)定方法，用于求解手眼旋轉(zhuǎn)矩陣和平移矩陣。徐成剛等[11]基于馬達(dá)代數(shù)空間構(gòu)建手眼標(biāo)定方程，并利用SVD方法求解手眼關(guān)系矩陣，取得了較好的效果。

受上述相關(guān)研究的啟發(fā)，本文提出一種新的基于主動視覺的自標(biāo)定方法，簡化攝像機(jī)旋轉(zhuǎn)的次數(shù)，降低了運(yùn)算的復(fù)雜度，能夠滿足工業(yè)領(lǐng)域的精度要求。

1 標(biāo)定原理

1.1 攝像機(jī)內(nèi)參矩陣

攝像機(jī)成像系統(tǒng)原理如圖1所示，特征點(diǎn)M在CCD成像平面O-uv中的成像點(diǎn)坐標(biāo)為MUV(u,v)，在圖像平面ON-XNYN中的成像點(diǎn)坐標(biāo)為MN(xn,yn)，在攝像機(jī)坐標(biāo)系OC-XCYCZC中的坐標(biāo)為MC(xc,yc,zc)。

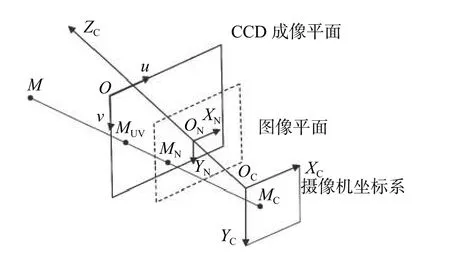
圖1 攝像機(jī)成像系統(tǒng)原理圖

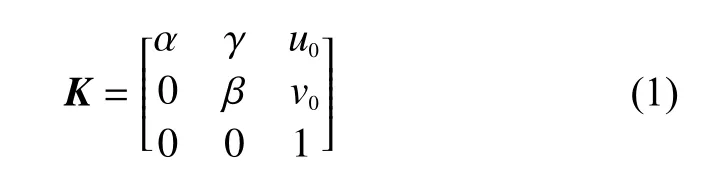
K是攝像機(jī)內(nèi)參矩陣五參數(shù)模型，圖像平面x軸、y軸的尺度因子分別用表示，表示畸變因子，(u0,v0)是CCD成像平面的原點(diǎn)。攝像機(jī)成像系統(tǒng)中坐標(biāo)變換關(guān)系如下：

1.2 坐標(biāo)關(guān)系轉(zhuǎn)換

基于主動視覺的手眼系統(tǒng)如圖2所示。其中，特征點(diǎn)M在世界坐標(biāo)系OW-XWYWZW中的坐標(biāo)為MW(xw,yw,zw)，在機(jī)械手末端坐標(biāo)系OH-XHYHZH中的坐標(biāo)為MH(xh,yh,zh)，在攝像機(jī)坐標(biāo)系OC-XCYCZC中的坐標(biāo)為MC(xc,yc,zc)。

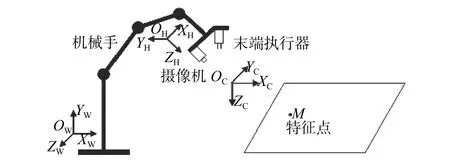
圖2 基于主動視覺的手眼系統(tǒng)原理圖

綜合式(1)～式(5)，得到手眼系統(tǒng)中的坐標(biāo)變換關(guān)系，其中ξ表示特征點(diǎn)在攝像機(jī)坐標(biāo)系的深度值。

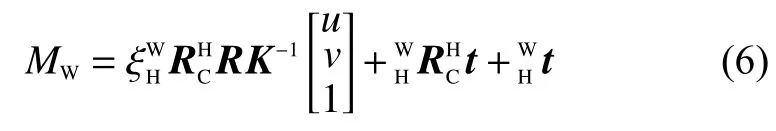
1.3 擴(kuò)展焦點(diǎn)

根據(jù)擴(kuò)展焦點(diǎn)的性質(zhì)[12]，任一特征點(diǎn)在攝像機(jī)平移前后的對應(yīng)點(diǎn)連線均通過擴(kuò)展焦點(diǎn)，因此可以通過場景中的2個或2個以上特征點(diǎn)來求解擴(kuò)展焦點(diǎn)。

如圖3所示，圖像I和圖像II是攝像機(jī)平移前后的兩幅圖像，P1和P2是特征點(diǎn)M在平移前后圖像上的位置。攝像機(jī)做平移運(yùn)動，直線OCO和OC'O'平行，直線P2'O和P2O'平行。P2'是P2在圖像I上的對應(yīng)點(diǎn)，對應(yīng)點(diǎn)連線P2'P1和OCOC'相交于擴(kuò)展焦點(diǎn)e。

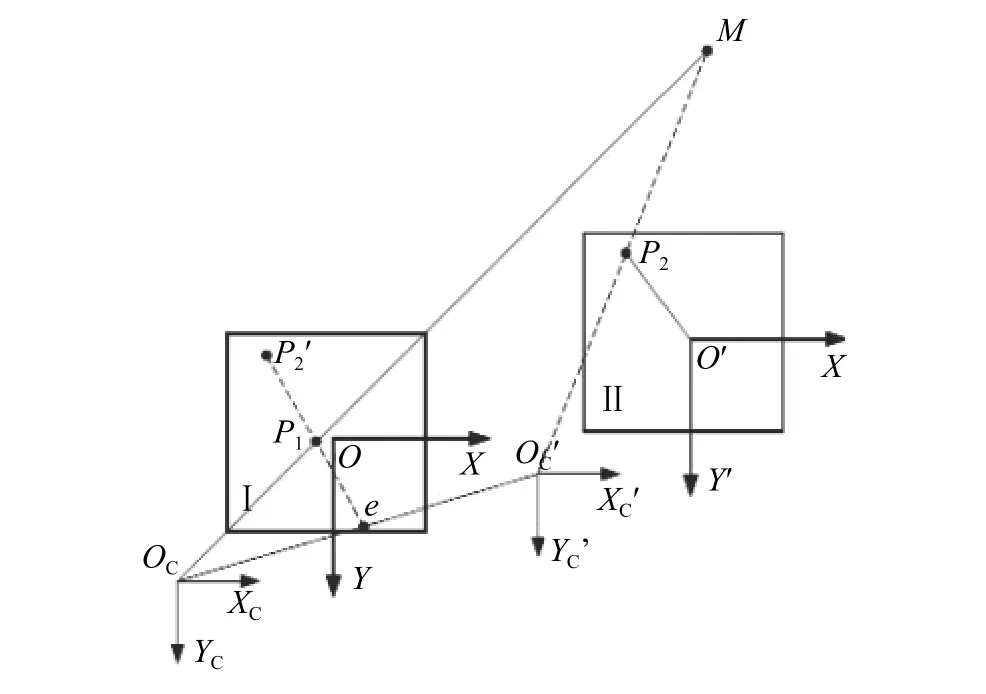
圖3 擴(kuò)展焦點(diǎn)的原理圖

由式(2)和式(3)，可得擴(kuò)展焦點(diǎn)e在攝像機(jī)坐標(biāo)中的坐標(biāo):

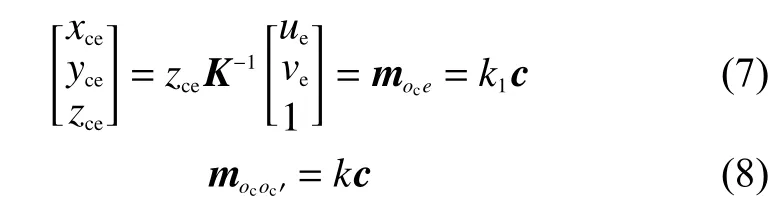
式中moce表示OC到e的向量，mococ′表示OC到OC′的向量，c=moce/|moce|，表示攝像機(jī)平移運(yùn)動的單位向量，且k>k1>0。

2 手眼關(guān)系旋轉(zhuǎn)矩陣的標(biāo)定

控制攝像機(jī)做1次平移運(yùn)動，XH1、XH2是平移前后特征點(diǎn)M在機(jī)械手末端坐標(biāo)系中的坐標(biāo)，XC1、XC2是平移前后特征點(diǎn)M在攝像機(jī)坐標(biāo)系中的坐標(biāo)，則有：

式(10)-式(9)，可得：

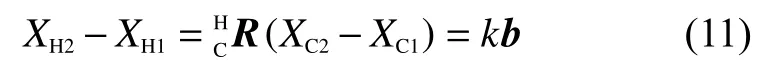
式(11)結(jié)合式(8)，可得：

如式(12)所示，控制機(jī)械手做3次線性無關(guān)的平移運(yùn)動，可得：

式中B=(b1,b2,b3)，C=(c1,c2,c3)，可得手眼關(guān)系旋轉(zhuǎn)矩陣為

式(14)表明，通過精確控制攝像機(jī)做3次線性無關(guān)的平移運(yùn)動，可以標(biāo)定手眼關(guān)系的旋轉(zhuǎn)矩陣，且為正交陣。

3 攝像機(jī)內(nèi)參矩陣的標(biāo)定

式(7)結(jié)合式(12)，可得：

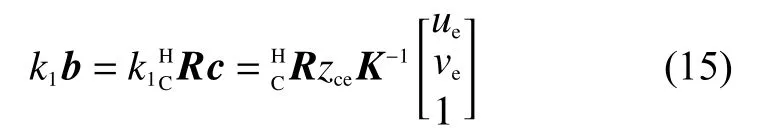
式(15)等價于：

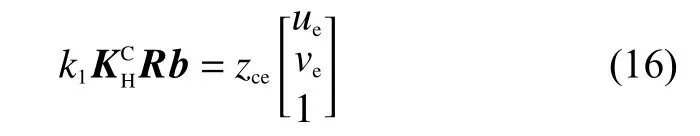
假定

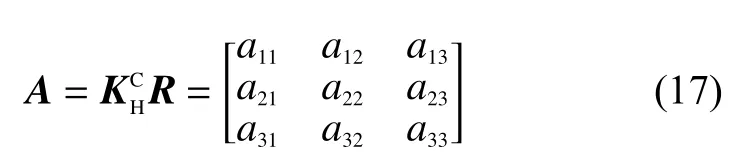
結(jié)合式(16)和式(17)，可得：

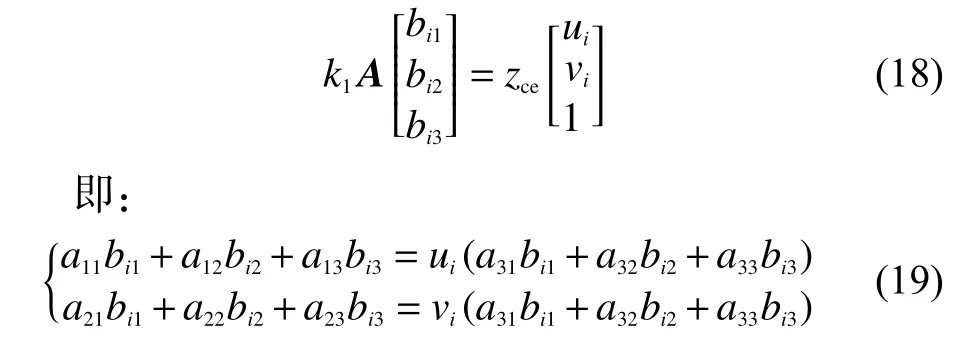
如式(18)和式(19)所示，假定另一矩陣A′除外其余元素與A相同，控制攝像機(jī)做4次線性無關(guān)的平移運(yùn)動，可通過最小二乘法求出A′的唯一解。為了確定a33的值，由式(17)得：

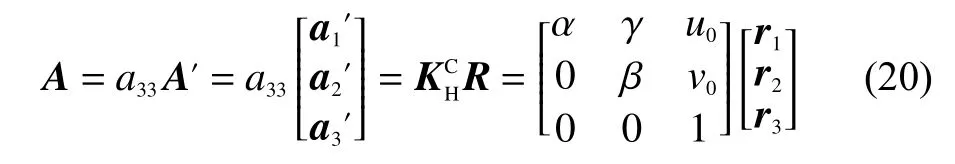
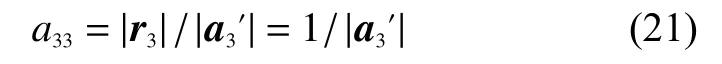
求出a33后，再由式(20)求出A，實(shí)現(xiàn)攝像機(jī)內(nèi)參矩陣的標(biāo)定。

4 特征點(diǎn)目標(biāo)深度的標(biāo)定

如圖1所示，控制攝像機(jī)做1次平移運(yùn)動，(u1,v1)和(u2,v2)是平移前后特征點(diǎn)M在CCD成像平面的坐標(biāo)，(x1,y1)和(x2,y2)是平移前后特征點(diǎn)M在圖像平面的坐標(biāo)，MC1(xc1,yc1,zc1)和MC2(xc2,yc2,zc2)是平移前后特征點(diǎn)M在攝像機(jī)坐標(biāo)系中的坐標(biāo)，由式(2)、式(3)和式(8)得：

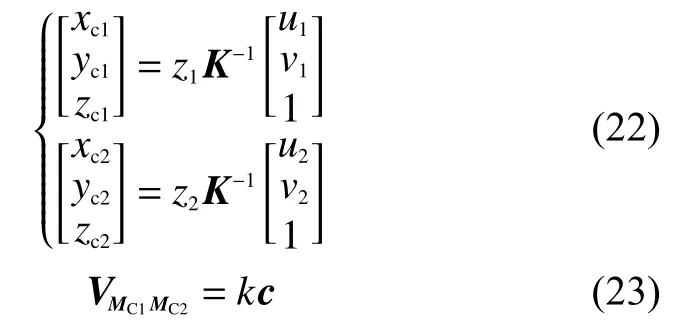
結(jié)合式(1)，將式(22)代入式(23)，可得：

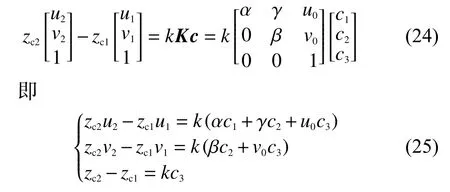
化簡式(25)，可得：

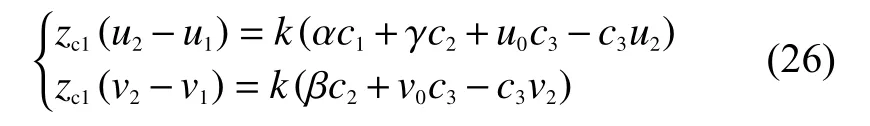
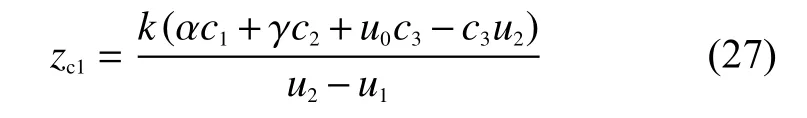
同理，通過式(26)可以求出zc2的值。同時式(26)、式(27)也表明通過控制攝像機(jī)做1次平移運(yùn)動，可以求出平移前后特征點(diǎn)的目標(biāo)深度信息。

5 手眼關(guān)系平移向量的標(biāo)定

完成上述4次線性無關(guān)的平移之后，為了標(biāo)定手眼關(guān)系的平移向量，可以先控制機(jī)械手做1次實(shí)旋轉(zhuǎn)運(yùn)動（姿態(tài)1→姿態(tài)2，如圖4所示），然后再控制攝像機(jī)做1次虛擬旋轉(zhuǎn)運(yùn)動（姿態(tài)2→姿態(tài)3，如圖5所示）。

同時需要注意的是，由于手眼系統(tǒng)中攝像機(jī)被固定在機(jī)械手末端，為了使旋轉(zhuǎn)前后機(jī)械手末端坐標(biāo)系和攝像機(jī)坐標(biāo)系的旋轉(zhuǎn)部分平移部分保持一致，實(shí)際是不能控制攝像機(jī)基于機(jī)械手末端完成姿態(tài)2→姿態(tài)3的旋轉(zhuǎn)操作。因此，圖5所示的只是假想控制攝像機(jī)做1次虛擬旋轉(zhuǎn)運(yùn)動，并基于此次虛擬旋轉(zhuǎn)做進(jìn)一步的標(biāo)定分析，同時還需保證虛擬旋轉(zhuǎn)結(jié)束后的攝像機(jī)坐標(biāo)系與實(shí)旋轉(zhuǎn)之前攝像機(jī)坐標(biāo)系的各個數(shù)軸平行且方向完全一致。

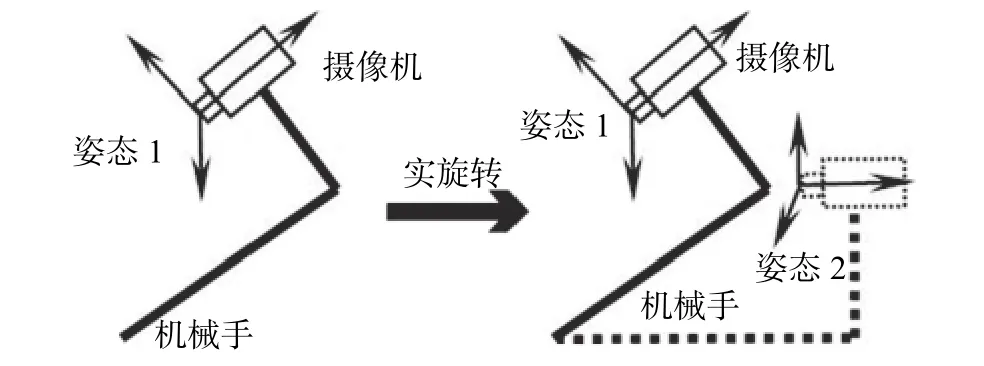
圖4 實(shí)旋轉(zhuǎn)前后手眼系統(tǒng)姿態(tài)對比

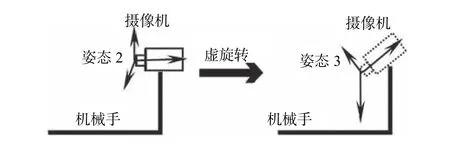
圖5 虛旋轉(zhuǎn)前后手眼系統(tǒng)姿態(tài)對比

XH5、XH6是實(shí)旋轉(zhuǎn)前后特征點(diǎn)M在機(jī)械手末端坐標(biāo)系中的坐標(biāo)，XC5、XC6是實(shí)旋轉(zhuǎn)前后特征點(diǎn)M在攝像機(jī)坐標(biāo)系中的坐標(biāo)。則有：

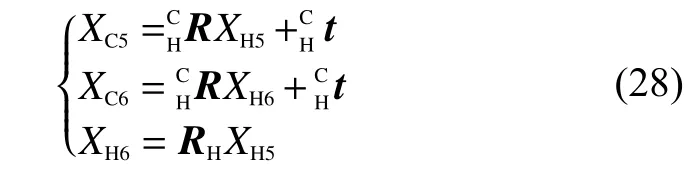
由式(28)，可得：

如圖5所示，虛旋轉(zhuǎn)完成后，特征點(diǎn)M在機(jī)械手末端坐標(biāo)系中的坐標(biāo)是XH7，在攝像機(jī)坐標(biāo)系中的坐標(biāo)是XC7，可得：

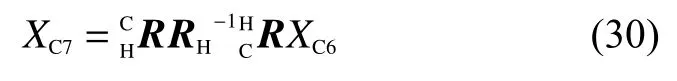
結(jié)合式(29)和式(30)，可得：

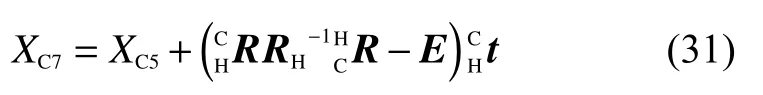
式(31)表明經(jīng)過一次實(shí)旋轉(zhuǎn)和一次虛旋轉(zhuǎn)后，特征點(diǎn)M在攝像機(jī)坐標(biāo)系中的坐標(biāo)XC5(xc5,yc5,zc5)和XC7(xc7,yc7,zc7)，可以看作是一次平移運(yùn)動前后的坐標(biāo)變換。

結(jié)合式(2)、式(3)和式(30)，可得

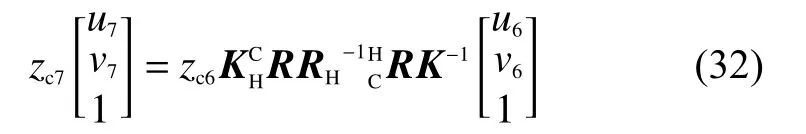
假定

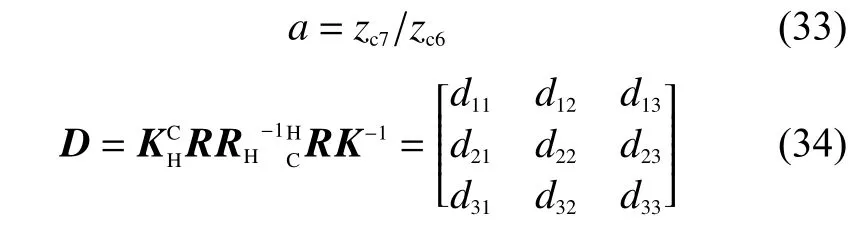
將式(33)和式(34)代入式(32)，可得：

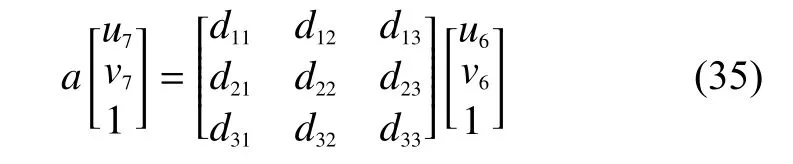
將式(35)展開，可得：

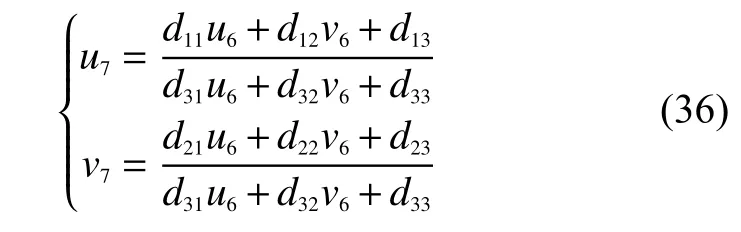
式(36)中，矩陣D的9個元素已知，(u6,v6)是機(jī)械手實(shí)旋轉(zhuǎn)后特征點(diǎn)M在CCD成像平面的坐標(biāo)，由此可以求出機(jī)械手虛旋轉(zhuǎn)后特征點(diǎn)M在CCD成像平面的坐標(biāo)(u7,v7)，進(jìn)而可以求出虛旋轉(zhuǎn)后特征點(diǎn)M在攝像機(jī)坐標(biāo)系的坐標(biāo)XC7(xc7,yc7,zc7)。

由式(2)、式(3)和式(8)得：

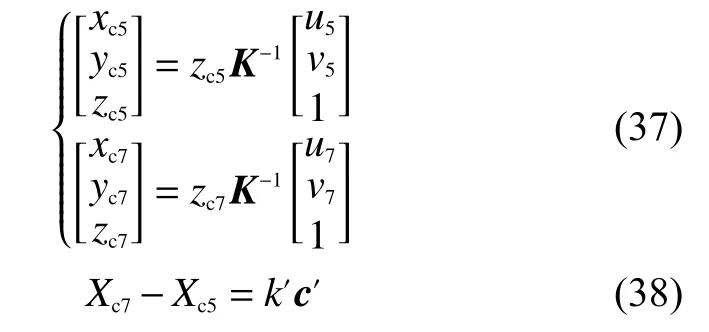
由于(u5,v5)→(u7,v7)的對應(yīng)關(guān)系類似于一次平移運(yùn)動，因此結(jié)合這兩點(diǎn)的坐標(biāo)可以求出平移運(yùn)動的單位向量c′。

將式(1)和式(37)代入式(38)，可得：

化簡式(40)，可得：

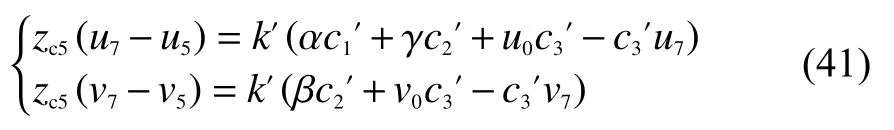
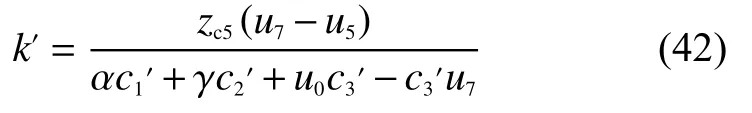
由式(43)可知，通過控制手眼系統(tǒng)中的機(jī)械手做一次實(shí)旋轉(zhuǎn)，然后再控制攝像機(jī)做一次虛旋轉(zhuǎn)，可以實(shí)現(xiàn)對手眼關(guān)系平移向量的標(biāo)定。

6 實(shí)驗(yàn)與精度分析

6.1 實(shí)驗(yàn)步驟

標(biāo)定實(shí)驗(yàn)的測試平臺采用的是DENSO VP-6242E/GM工業(yè)機(jī)器人，攝像機(jī)鏡頭的焦距為8 mm，感光CCD分辨率為640×480。

如圖6所示，首先控制攝像機(jī)做4次線性無關(guān)的平移運(yùn)動。為提高計算精度，取三特征角點(diǎn)對應(yīng)連線的均值[9]計算CCD成像平面中擴(kuò)展焦點(diǎn)的坐標(biāo)。

圖6 4次平移運(yùn)動

然后根據(jù)擴(kuò)展焦點(diǎn)的坐標(biāo)可以求出攝像機(jī)平移運(yùn)動過程中的方向向量，繼而求出手眼關(guān)系的旋轉(zhuǎn)矩陣和 攝像機(jī)內(nèi)參矩陣。

接著做1次實(shí)旋轉(zhuǎn)運(yùn)動，此次實(shí)旋轉(zhuǎn)結(jié)合1次假想的虛旋轉(zhuǎn)，可以求出手眼關(guān)系的平移矩陣為

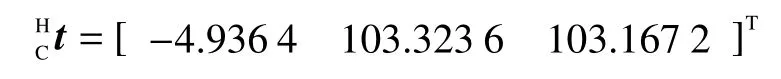
為了進(jìn)一步確保自標(biāo)定方法的正確性，最后還需在機(jī)械手末端安裝一個執(zhí)行器，同時計算該末端執(zhí)行器在機(jī)器人世界坐標(biāo)系中的偏移修正值ts。

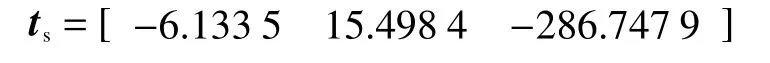
6.2 精度分析

在攝像機(jī)內(nèi)參矩陣、手眼關(guān)系旋轉(zhuǎn)矩陣和平移向量完成求解之后，在保持機(jī)器人本體姿態(tài)不變的情況下，進(jìn)行平面和三維數(shù)據(jù)驗(yàn)證測試，測試結(jié)果如表1所示。

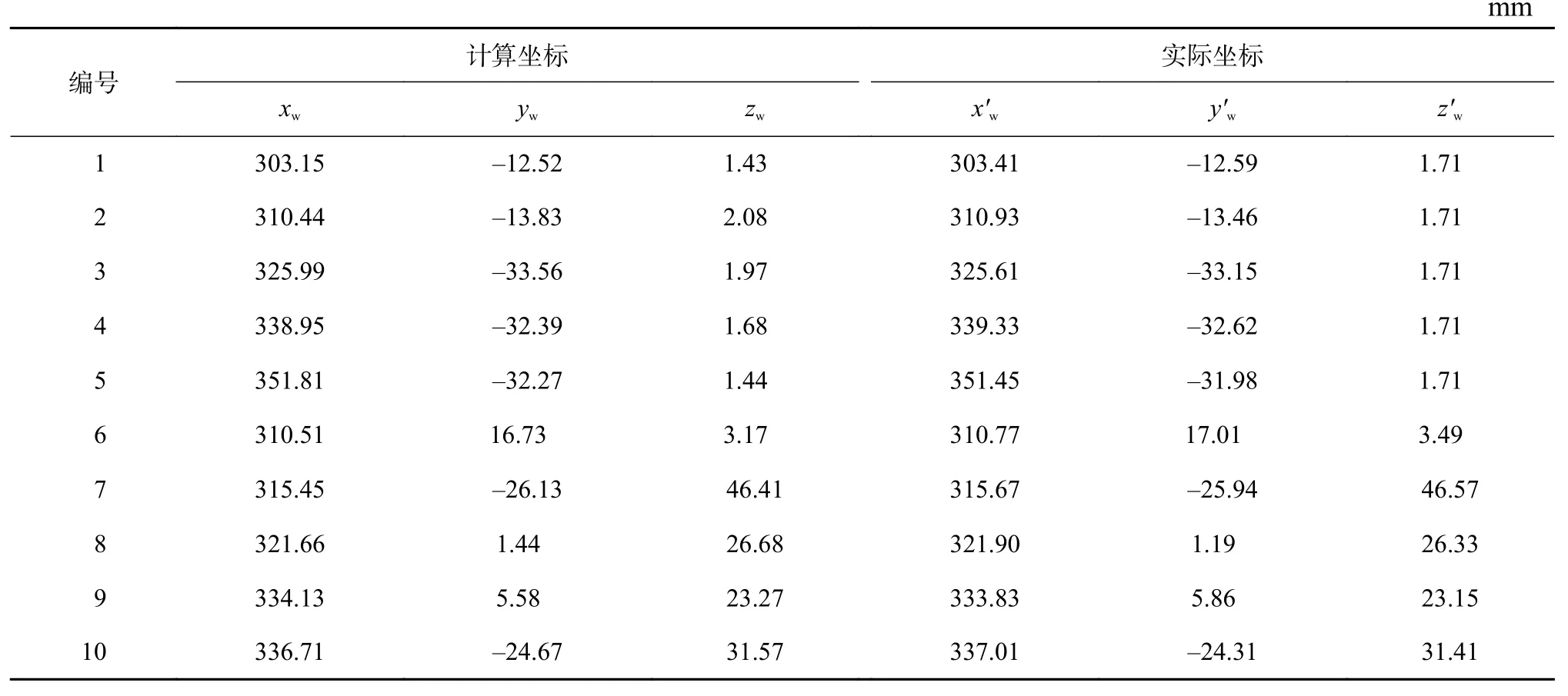
表1 測量精度分析

表1中的計算坐標(biāo)由手眼系統(tǒng)自標(biāo)定時相關(guān)特征點(diǎn)坐標(biāo)值計算得出，其中1～5號為平面測試數(shù)據(jù)，6～10號為三維測試數(shù)據(jù)，最大測量誤差均不超過0.40 mm，能夠滿足工業(yè)領(lǐng)域的精度要求。

7 結(jié)束語

與傳統(tǒng)手眼系統(tǒng)自標(biāo)定方法相比，提出的基于主動視覺的手眼系統(tǒng)自標(biāo)定方法無需標(biāo)定參照物，實(shí)現(xiàn)過程相對簡單，并在2個方面對做了較好的改進(jìn)：1）通過控制攝像機(jī)做3次線性無關(guān)的平移運(yùn)動，即可實(shí)現(xiàn)對手眼關(guān)系旋轉(zhuǎn)矩陣的線性求解，比文獻(xiàn)[6]簡化了1次平移運(yùn)動，降低了手眼關(guān)系旋轉(zhuǎn)矩陣以及后續(xù)攝像機(jī)內(nèi)參矩陣求解的運(yùn)算復(fù)雜度；2）與文獻(xiàn)[9]相比，本方法簡化了1次實(shí)旋轉(zhuǎn)，只需1次實(shí)旋轉(zhuǎn)結(jié)合1次虛旋轉(zhuǎn)即可，降低了求解手眼關(guān)系平移向量的運(yùn)算復(fù)雜度。最后的實(shí)驗(yàn)結(jié)果表明，本方法能夠保證實(shí)際作業(yè)精度，對促進(jìn)手眼系統(tǒng)的工業(yè)應(yīng)用具有參考價值。