地下結構抗震設計的等效地震荷載動力有限元方法

吳 敏

(上海市城市建設設計研究總院(集團)有限公司， 200125， 上海//工程師)

隨著我國基礎建設的大力發展，城市地下空間被大量開發和利用。長期以來，人們普遍認為地下結構抗震性能優于地面結構[1]。直到1995年日本阪神大地震中，大開站等地下結構遭受嚴重震害，地下結構抗震設計才逐漸引起工程設計人員的重視。

目前，簡化抗震設計方法依然是工程設計人員進行地下結構抗震設計的主要手段。而開展簡化抗震設計的第一步是計算等效地震荷載，即進行土層地震反應分析。過去，人們開發出了等效線性化程序(如經典的Shake91)進行一維土層地震反應分析。研究表明，等效線性化方法不能反應土層真實的運動過程，在輸入地震動強度較大時，計算誤差較大，甚至還可能出現死循環現象[2]。此外，筆者通過長期實踐發現，與動力時程法相比，采用等效線性化程序計算所得等效地震荷載進行抗震分析時，所得的結構內力總是偏小，等效線性化方法的準確性受到質疑。如今，有限元方法廣為人知。《城市軌道交通結構抗震設計規范》[3](GB 50909—2014)中指出，動力有限元方法可以用于自由場的地震反應分析，但缺乏具體要求。人們對于如何準確采用動力有限元方法進行土層地震反應分析知之甚少。

本文以上海某地下結構為工程依托，采用大型通用有限元軟件ABAQUS進行二維自由場地震反應分析，詳細介紹了建模過程及其要點，并以傳統等效線性化程序EduShake為對照，驗證了該方法的有效性。對于從事地下結構抗震的工程設計人員及相關學者具有指導意義。

1 等效地震荷載

簡化抗震設計方法的基本思想是：地下結構受到周圍土層的約束，而地層在地震作用下存在峰值響應，在該響應下結構的內力響應也最大。因此，多數簡化抗震設計方法本質上是通過計算自由場在地震作用下的動力響應，從而選取合適的力或位移形式的最不利地層響應作為等效地震荷載，再通過靜力的方式計算結構在地震作用下的真實受力情況。可見，等效地震荷載將復雜的結構動力問題轉化為易于計算且能滿足工程設計需求的靜力問題。

表1列舉了目前我國規范或學術界討論較多的幾種地下結構簡化抗震設計方法及其采用的等效地震荷載形式。基于土層位移和土層加速度2個主要方向的研究，均已研究出了多種簡化抗震設計方法。

表1 常見地下結構簡化抗震設計方法及其等效地震荷載

2 運用動力有限元求解等效地震荷載

2.1 計算模型

以上海某地下結構所在地質斷面為例，運用大型通用有限元軟件ABAQUS，建立長為500 m、高為60.5m的二維平面應變模型。經過對比，本文未采用無限元邊界，而以中間密兩側疏的網格劃分方式來減小地震波在邊界處的激蕩效應。根據ABAQUS軟件幫助文檔，無限元對于水平入射的地震波的吸收作用有限甚至會引起震蕩。模型中土體采用平面四節點單元(CPE4R)，本構模型采用摩爾庫倫模型。場地自重應力采用ABAQUS軟件的自動地應力平衡技術來模擬，自由場平衡后的土層變形可達到10-6m。

在對照組EduShake軟件中建立相同的土層模型，土體的非線性動力特性采用程序中Sun等建議的黏土曲線。地震波選擇常用的El-centro波。EduShake軟件在計算過程中會自動濾除頻率大于20 Hz的地震波成分，所以對于輸入ABAQUS軟件的地震波需做同樣的濾波處理。處理后的El-centro波時程曲線如圖1所示，計算時將峰值加速度調幅至0.1g后沿模型底部水平輸入。

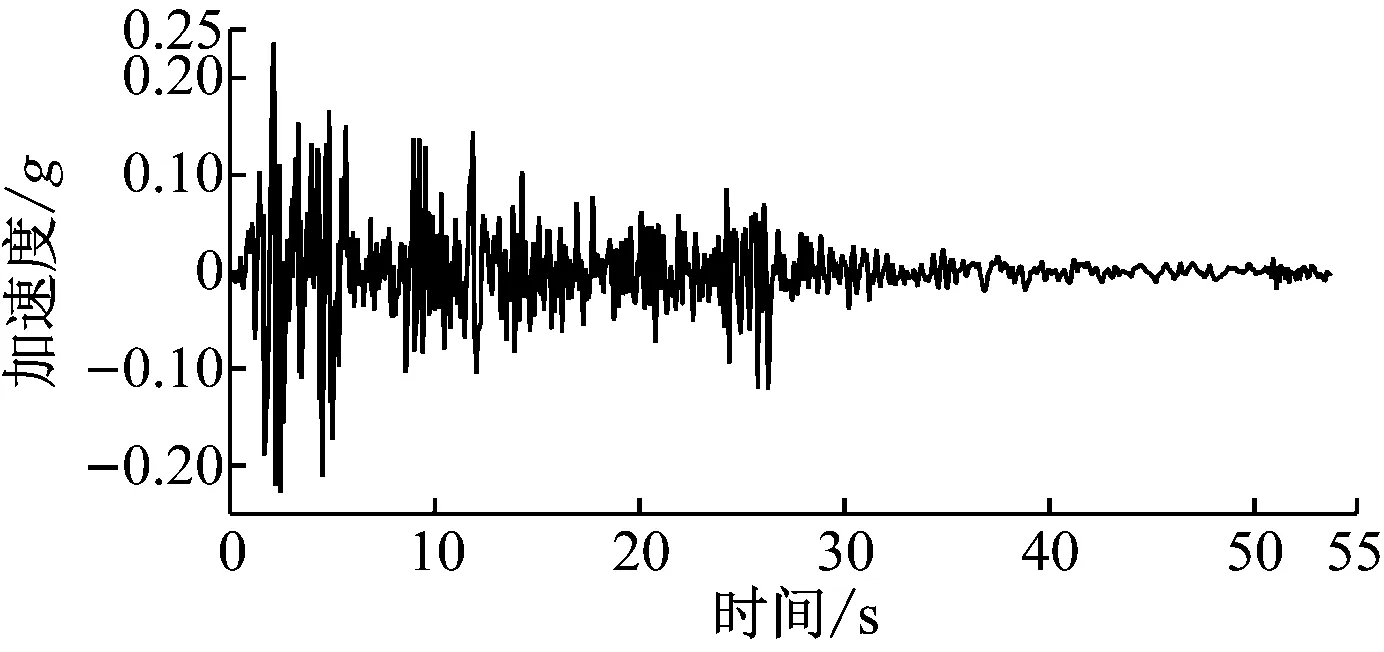
圖1 El-centro波時程曲線

2.2 關鍵參數

土層動力非線性問題是采用ABAQUS軟件進行自由場地震反應分析的要點。ABAQUS軟件中，土體動力非線性本構模型的建立需要二次開發，較為復雜。因此，文獻[6]以等效線性化程序計算反饋出的等效剪切模量及等效阻尼比來近似考慮該問題。

等效剪切模量可以換算為彈性模量輸入土層摩爾庫倫模型中，土層阻尼可通過定義材料瑞麗阻尼來實現。首先采用ABAQUS軟件線性懾動分析步對場地進行模態分析，計算得出工程場地的前兩階陣型頻率f1=0.321 Hz，f2=0.865 Hz。再通過公式(1)即可計算得出瑞麗阻尼中的α系數和β系數。

式中：

ξ——等效阻尼比。

最終，ABAQUS軟件自由場動力時程分析中土層的物理力學參數如表2所示。

2.3 結果對比

本節從單點對比、最不利時刻土層側移曲線及加速度曲線對比兩個角度，比較了ABAQUS軟件動力時程分析與等效線性化程序EduShake軟件的計算結果，從而驗證動力有限元計算的有效性。

2.3.1 單點對比

通常，地震波在向上傳播的過程中具有明顯的放大效應，模型上部的土層加速度響應、位移響應最大。在模型的頂部與中部分別選取2個單元節點，其中頂部位置與中間位置的加速度響應、位移響應對比分別如圖2、圖3所示。從圖中可以看出，

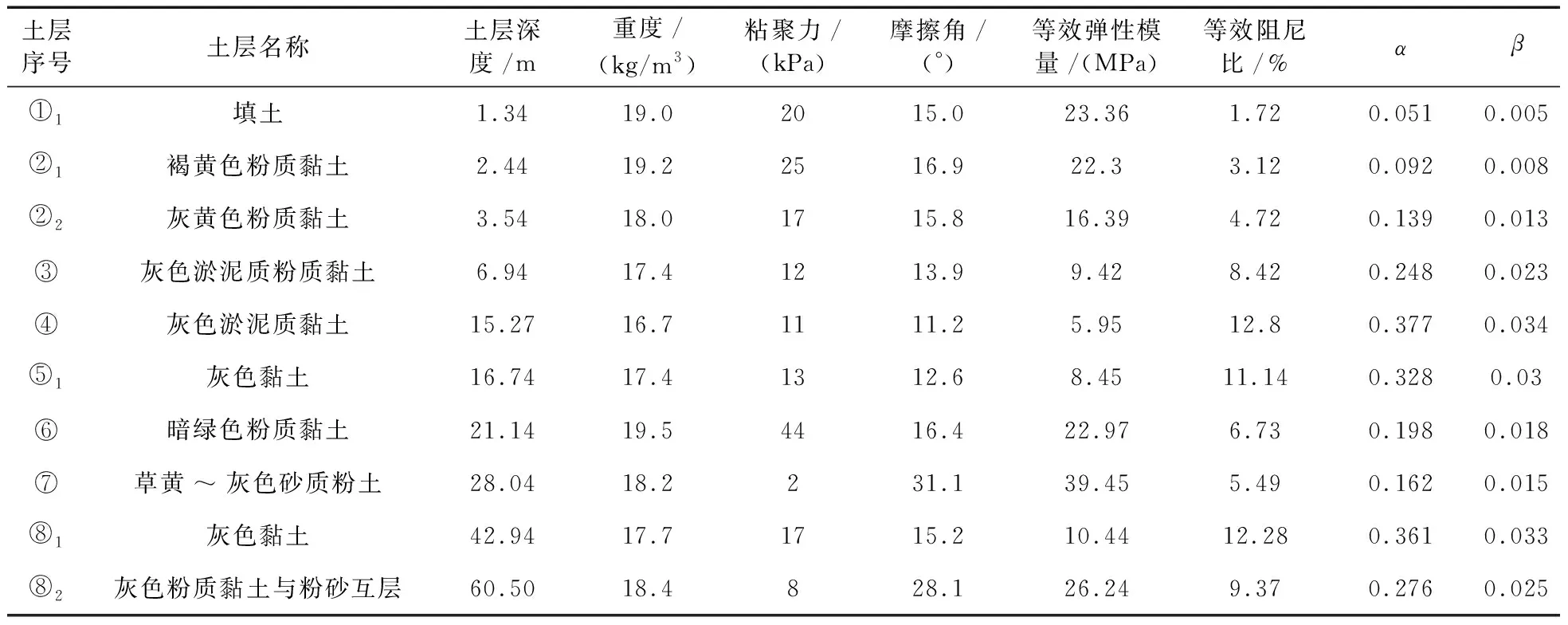
表2 ABAQUS軟件中輸入的土層參數

ABAQUS軟件計算所得土層在地震作用下的加速度響應與EduShake軟件的計算結果基本吻合，頂部峰值加速度誤差僅為1.58%，而腰部峰值加速度誤差為1.72%；水平位移時程曲線總體上基本吻合，頂部峰值側移誤差為6.07%，腰部峰值側移誤差為9.49%。這驗證了本文運用動力有限元ABAQUS軟件進行自由場地震反應分析的有效性與正確性。

a) 土層加速度時程

b) 土層位移時程圖2 模型頂部動力響應對比圖

2.3.2 最不利時刻分布曲線對比

地下結構在地震波的作用下，總會達到某一個最不利時刻，該瞬時結構的側向變形最大，結構動力響應也最大。該車站結構埋深約3 m，結構高度約為10 m，計算自由場模型中結構頂底板位置處的土層水平位移差，取其峰值位移差所對應的時刻為該結構的最不利時刻。本例最不利時刻為17.6 s，該時刻土層反應加速度與反應位移沿深度的分布曲線如圖4所示。總體來講，ABAQUS軟件與EduShake軟件的計算結果仍基本吻合，但是誤差相對單點對比時明顯增大。土層反應加速度的平均計算誤差為25.9%，土層位移的平均計算誤差為19.4%。誤差增大是由這兩個分析過程的相位差積累造成的。同時，圖4顯示出淺層土層對地震加速度具有明顯的放大作用，但是淺層的峰值加速度不一定大于更深層土層的峰值加速度，這與淺層地下結構震害明顯大于深層地下結構的現象相違背。因而，完全基于結構慣性力所建立的地下結構簡化抗震設計方法慣性力法已被《城市軌道交通結構抗震設計規范》(GB 50909—2014)等規范淘汰[4]。相反，在地震作用下土層反應位移的分布曲線規律較明顯，基本呈現倒三角型，所以某些學者抓住該特點提出了更為優化的地下結構簡化抗震設計方法——整體強制反應位移法[5]。

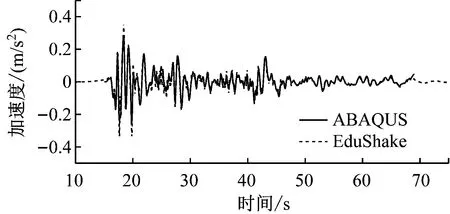
a) 土層加速度時程

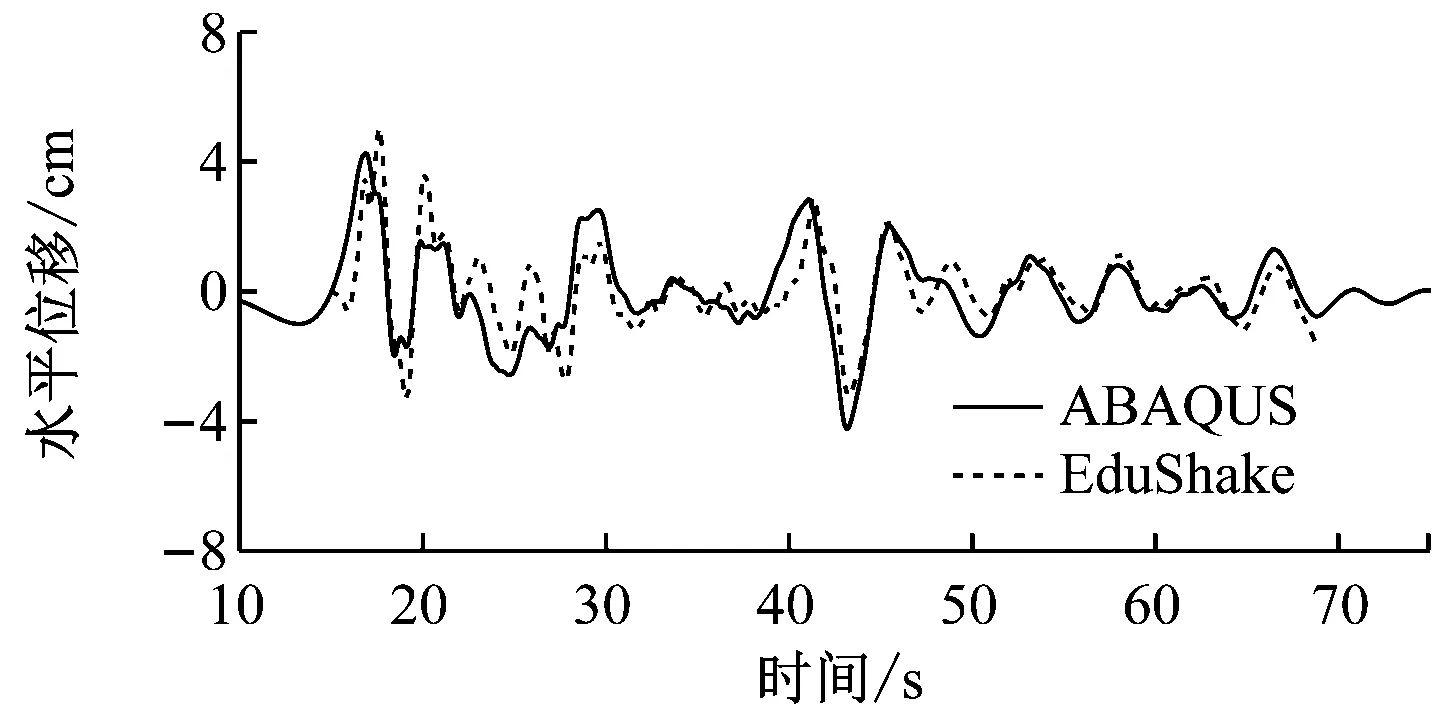
b) 土層位移時程圖3 模型中部動力響應對比圖

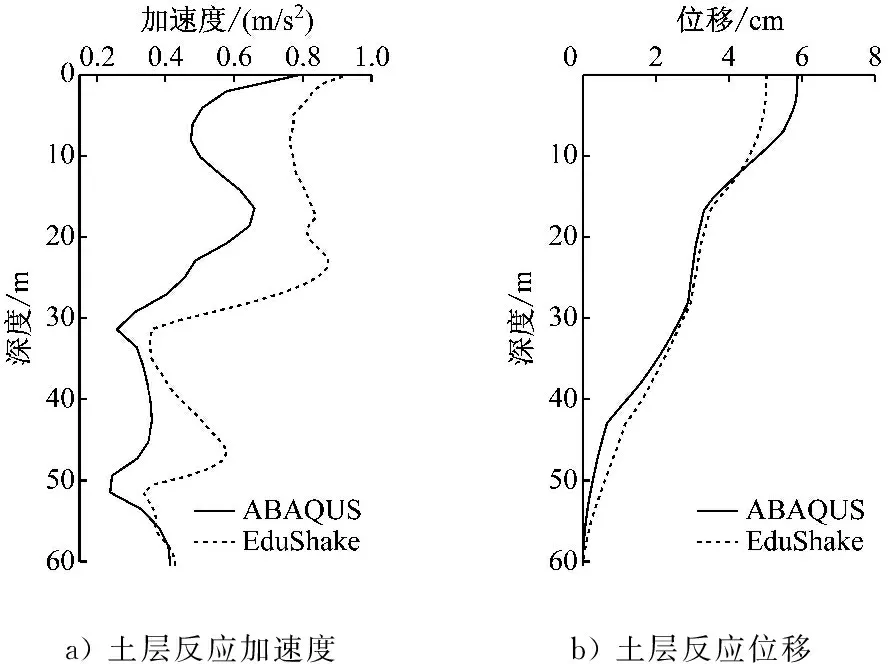
a) 土層反應加速度b) 土層反應位移

圖4 最不利時刻土層反應沿深度的分布曲線

3 結語

本文基于大型通用有限元軟件ABAQUS，以動力有限元方法開展了地下結構簡化抗震設計中等效地震荷載的數值模擬，并將其計算結果與傳統的等效線性化程序EduShake軟件的計算結果作對比，得出以下成果：

(1) 動力有限元法計算所得的單點加速度時程曲線、位移時程曲線與EduShake軟件計算的結果相比，偏差較小；最不利時刻的加速度與位移沿深度的分布曲線偏差相對較大，但曲線走勢基本相同。

(2) 考慮土層等效剪切模量與阻尼之后，ABAQUS軟件計算所得的土層地震反應與EduShake軟件的計算結果基本吻合，驗證了該方法在等效地震荷載計算中的有效性與正確性。

(3) 以動力有限元法進行二維土層地震反應分析更為直觀、簡便，其豐富的后處理方式也有利于設計人員展開抗震研究及工程設計。