銅始極片預剝離技術的研究

鐘 晨，孫東明，蔣龍飛，莫翰林

(昆明理工大學 機電工程學院，云南 昆明 650500)

0 引 言

傳統的電解銅生產水平已經不能滿足目前的市場需求。國外的銅冶煉企業早在20世紀20年代就開始了電解銅自動化生產線的研究。近些年，國內的冶煉廠也加大了該領域投入。其中，銅始極片及電解銅的剝離是研發自動化生產線的關鍵[1-2]。在始極片的剝片工藝中，剝離裝置設計有預剝離、完全剝離兩個工序，預剝離是完全剝離的前置工序，其核心部件為撓曲裝置，即對種板施加一個撓曲力使種板產生一個彎曲力矩從而使附著在種板上的銅始極片端部產生開口。如果預剝離失敗，則完全剝離無法繼續進行，嚴重影響生產效率[3]。

為提高始極片的剝離成功率、減少返工工作量、延長鈦種板的使用壽命，本文將對始極片預剝離技術進行研究。

1 始極片結合界面應力計算

傳統法生產陰極銅必須先制作銅始極片，目前許多銅冶煉廠生產銅始極片所用的種板為鈦種板。因此，以鈦種板為例，分析撓曲力作用在鈦板的中間位置(x=0處)時，銅始極片與鈦板結合界面的切向剪應力，及下層銅始極片上的橫向剪應力。

板結構在撓曲力F作用下的計算模型如圖1所示。

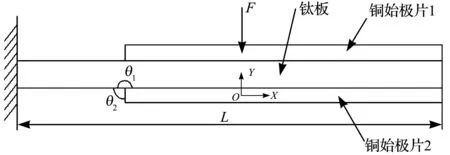
圖1 板結構力學模型

在如圖1所示的撓曲力的作用下，由于結合界面端附近的剪應力比較大，并且界面端附近具有應力奇異性，銅始極片2與鈦種板結合界面的界面端處會率先分離開[4]。作用在板結構上的撓曲力使板結構發生彎曲，板結構所受撓曲力近似均勻分布在一條直線上，在板的撓曲變形比較小時，將板沿縱向分成若干份，各小份可以看作矩形等截面梁。因此，本研究對細分成的梁用材料力學的彎曲理論進行應力分析。由于板在橫向受力均勻，細分后梁的彎曲正應力、撓度、切應力可以代表板的應力情況。

研究對象為夾層等截面直板，中間層比表面層稍厚。當板結構受到橫向集中載荷的作用時，對夾層板單元進行受力分析，除了要考慮剪力、彎矩以外，還要考慮層間剪切力和軸向拉力的作用[5-12]。夾層板下表層受力分析如圖2所示。

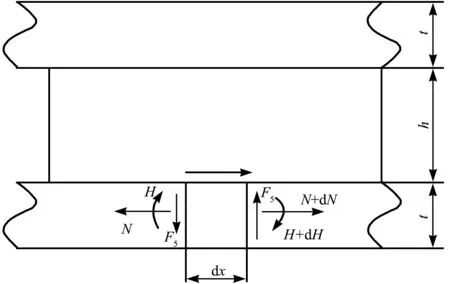
圖2 夾層板微元受力平衡

參考圖2，由夾層板微單元的彎矩平衡和x方向的力平衡方程得到：

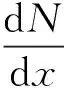
(1)

(2)

式中：τ—剪應力；b—截面寬度；h—鈦板厚度；F—撓曲力。

由(2)式得：夾層板與均質板的區別在于，夾層板的彎矩不僅與橫向剪力有關，還與層間剪切力有關。

夾層板的上下表層受到彎矩和軸向力的作用，應用Euler-Bernoulli理論進行分析，可得應力應變關系：

(3)

(4)

式中：E—彈性模量；t—始極板厚度；u—夾層板軸向的位移；v—夾層板橫向的位移。

由式(1～4)得:

(5)

(6)

式中：u—夾層板軸向的位移；v—夾層板橫向的位移；E—彈性模量；t—始極板厚度；b—截面寬度；h—鈦板厚度。

夾層板層間變形協調關系如圖3所示。

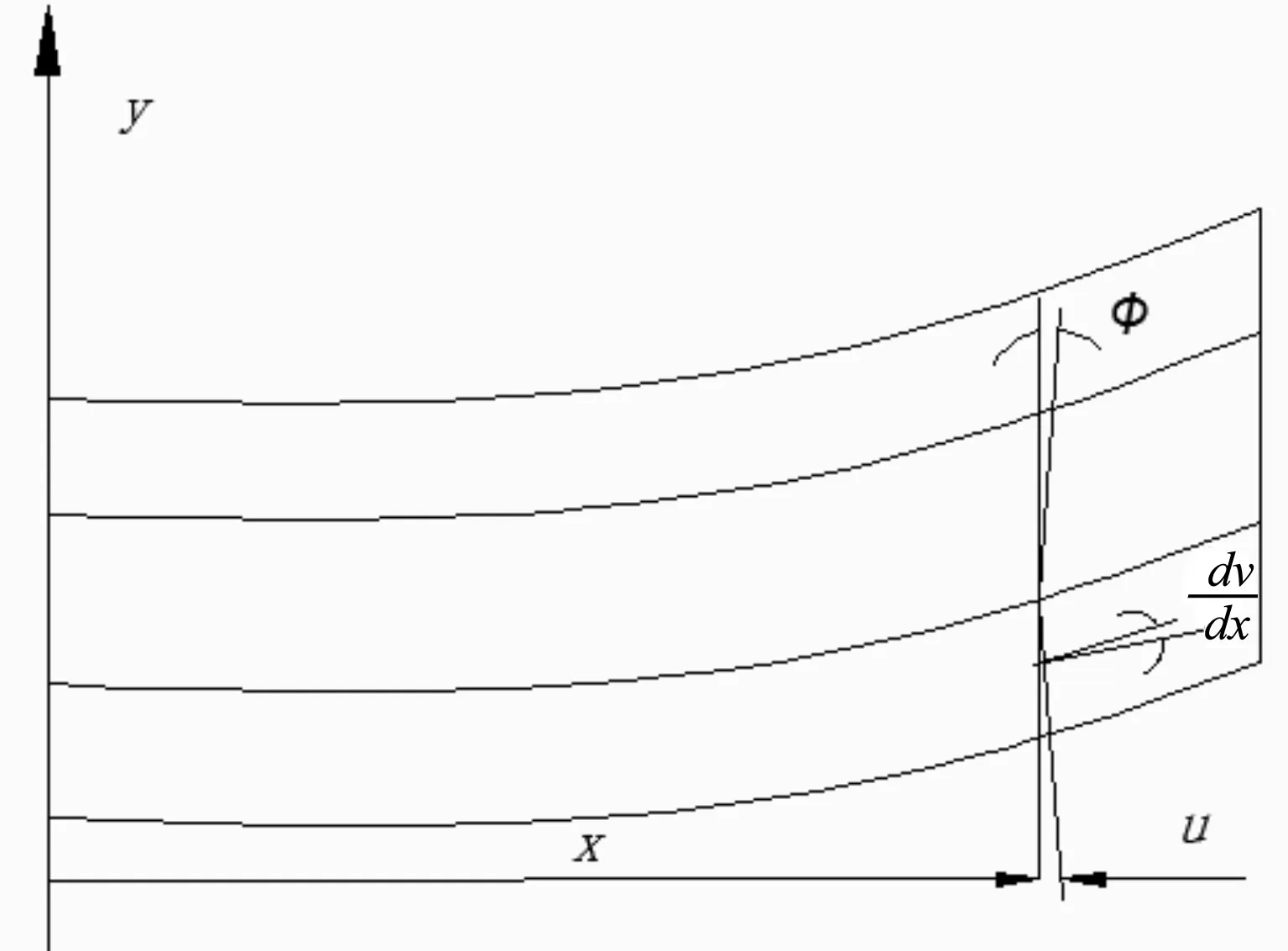
圖3 夾層板層間變形協調關系

由于面內剪切力的作用，中間層鈦板會發生剪切變形，依據上下表層與中間層的變形協調關系，剪切變形的角度為：

(7)

式中：φ—剪切變形的角度；u—夾層板軸向的位移；t—始極板厚度；h—鈦板厚度。

因此，層間剪切應力為：

(8)

式中：G—剪切模量；h—鈦板厚度；t—始極板厚度；u—夾層板軸向的位移；v—夾層板橫向的位移；φ—剪切變形的角度。

對式(8)求x二階導數，并將式(5，6)代入可得:

(9)

式中：G—剪切模量；h—鈦板厚度；t—始極板厚度；u—夾層板軸向的位移；v—夾層板橫向的位移；φ—剪切變形的角度；E—彈性模量；b—截面寬度；F—撓曲力。

解式(9)得到層間剪切力表達式為：

(10)

式中：h—鈦板厚度；t—始極板厚度；b—截面寬度；F—撓曲力。

(11)

式中：h—鈦板厚度；t—始極板厚度；b—截面寬度；E—彈性模量；G—剪切模量。

將邊界條件:x=0時，τ=0，代入式(10)可求得:

(12)

式中：h—鈦板厚度；t—始極板厚度；b—截面寬度；F—撓曲力。

對式(8,10)微分，并進行比較有：

(13)

式中：G—剪切模量；h—鈦板厚度；t—始極板厚度；u—夾層板軸向的位移；v—夾層板橫向的位移；φ—剪切變形的角度；E—彈性模量；b—截面寬度；F—撓曲力；N—軸力；M—彎矩。

由邊界條件：x=L/2時，M=N=0，結合式(13)可以求得:

(14)

式中：h—鈦板厚度；t—始極板厚度；L—跨度。

聯立式(12，14)解得常數A、B,并代入式(10)求得層間剪切力的表達式為:

(15)

式中：h—鈦板厚度；t—始極板厚度；L—跨度；b—截面寬度。

將式(15)代入式(1)積分并結合邊界條件(x=L/2時，N=0)求得軸力的表達式為：

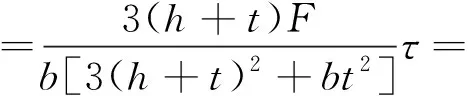
(16)

式中：h—鈦板厚度；t—始極板厚度；L—跨度；b—截面寬度；F—撓曲力。

將式(14)代入式(2)并對x積分，結合邊界條件(x=L/2時M=0)求得彎矩為:

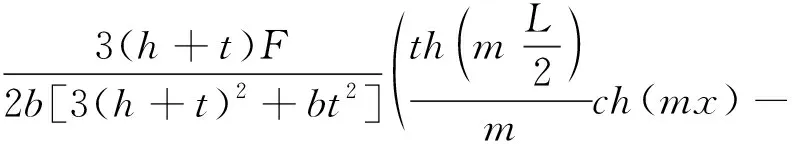
(17)

式中：h—鈦板厚度；t—始極板厚度；L—跨度；b—截面寬度；F—撓曲力。

下層銅始極片正應力計算如下：

(18)

式中：h—鈦板厚度；t—始極板厚度；L—跨度；b—截面寬度；F—撓曲力；N—軸力；M—彎矩。

下層銅始極片上橫向剪應力的分布表示為:

(19)

式中：h—鈦板厚度；t—始極板厚度；b—截面寬度；F—撓曲力；N—軸力；M—彎矩；τ—剪應力。

由于始極片的剝離涉及不同材料、接觸、大變形以及界面端的應力奇異性等非線性問題，很難使用理論分析的方法對結合界面的應力進行精確分析。

2 始極片預剝離過程仿真

2.1 建 模

本研究在Soild works中建立銅始極片預剝離機構的簡化模型，導入ANSYS Workbench中對始極片進行靜力學分析[13]。

簡化模型如圖4所示。

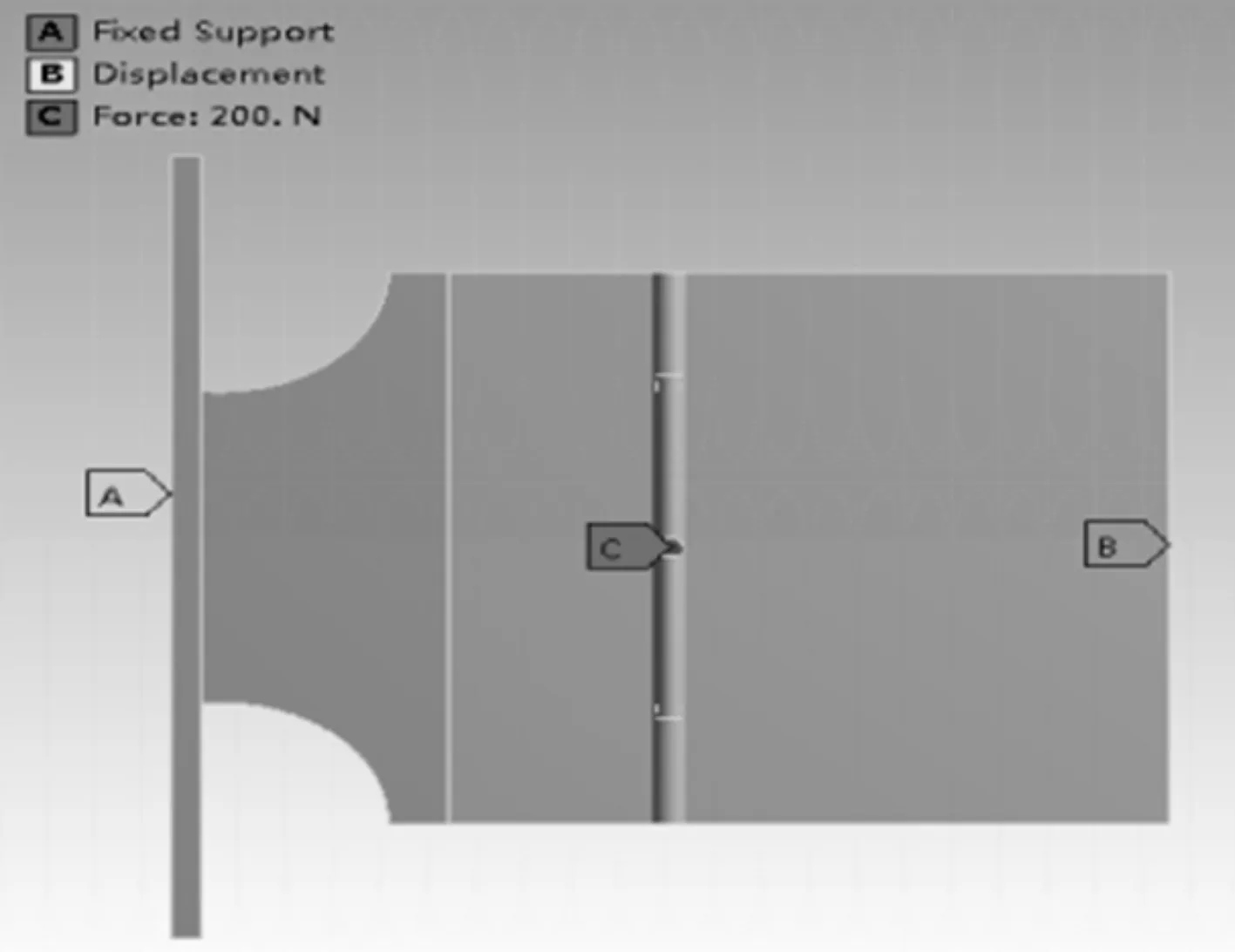
圖4 預剝離機構簡化模型

本研究在ANSYS中設置銅始極片彈性模量E=12.86 GPa，泊松比ν=0.36；鈦種板的彈性模量E=108，泊松比ν=0.33。由于銅始極片從鈦種板上剝離下來是因為受到油缸驅動的推桿的橫向力的作用，該仿真的力載荷施加在推桿上，力的類型為集中力，大小為200 N。

由于目前始極片的預剝離裝置中撓曲力機構通常設置在鈦種板長度方向的中間位置，距離銅始極片界面端1/4處。因此，本研究選取撓曲力作用位置和鈦種板厚度為變量，分析鈦板厚度和撓曲力作用位置的變化對銅始極片與鈦種板結合界面端的應力分布的影響，進而以應力值和撓度值作為評價指標，選出較優的有利于剝離的組合。

本文選取撓曲力的作用位置分別為銅始極片的中間位置(位置1)、鈦種板的中間位置(位置2)、距離銅始極片界面端1/4處(位置3)。由于厚度為2mm以下的鈦種板在撓曲力作用下容易變形，而鈦板厚度太大會造成浪費。因而，本研究選取鈦板的厚度分別為2 mm、3.25 mm、4.5 mm。綜合考慮力的作用位置和板厚，可得到9種組合，如表1所示。

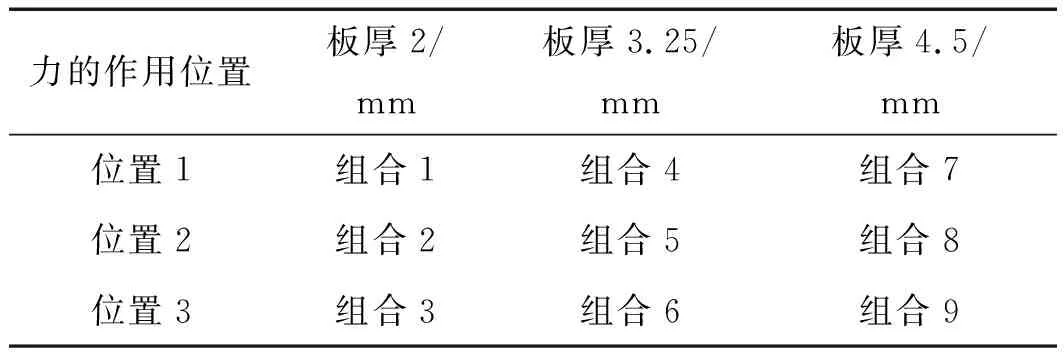
表1 撓曲力的作用位置和鈦板板厚的組合

2.2 始極片與鈦種板結合界面端應力及撓度分布

經ANSYS Workbench軟件分析后得出各組合的靜力學分析結果。組合1的銅始極片與鈦板結合界面端的橫向剪應力分布云圖及切向剪應力分布云圖如圖5所示(其他組合云圖相似)。

圖5 界面上沿寬度方向界面端的剪應力分布云圖(組合1)

9種不同組合下，銅始極片與鈦板組成的板結構沿厚度方向的撓度變化云圖如圖6所示。

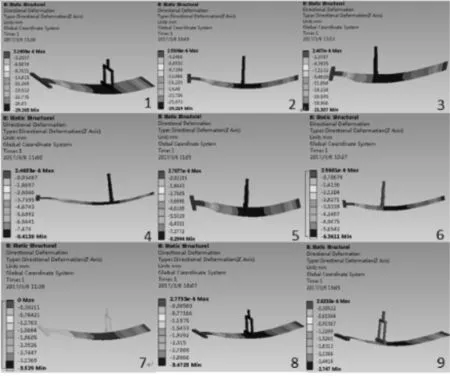
圖6 各組合沿厚度方向的撓度值分布云圖

圖中數字1到9表示組合1到組合9的撓度云圖的編號。

最后將所得仿真數據匯總，如表2所示。

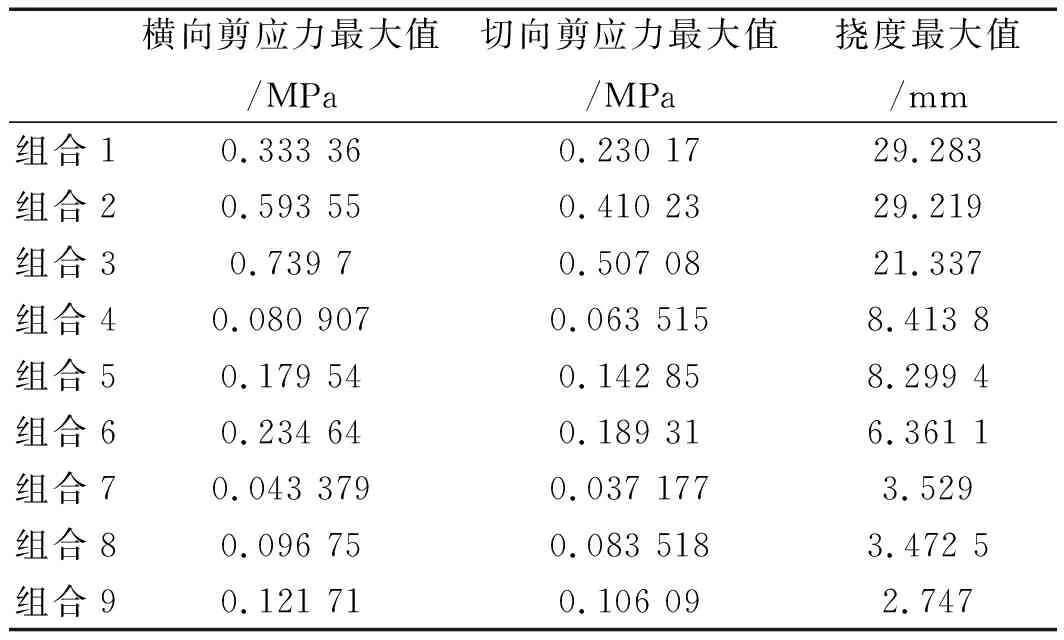
表2 各組合界面端剪應力及撓度最大值

2.3 實驗及結果分析

將仿真數據匯總得到表2，將表1的數據結合表2可以得出:在鈦板厚度不變的情況下，力的作用位置越靠近界面端，板結構的最大撓度值越小，界面端剪應力值越大。從表2可以看出:組合3的剪應力值比組合1和組合2的大，有利于剝離，而且組合3的最大撓度值比組合1和組合2小很多，對銅始極片和鈦板的撓曲損傷比組合1和組合2小，可以減少銅始極片后續矯直的工作量并延長鈦板的使用壽命，因此組合3相對組合1、組合2是較優選擇。同理，組合6相對于組合4、組合5是較優選擇，組合9相對于組合7、組合8是較優選擇。

在力的作用位置不變的情況下，鈦板厚度越大，板結構的最大撓度值越小，結合界面界面端的剪應力值越小，板厚越小，界面端剪應力及板結構撓度對板厚的變化越敏感。從表2中比較撓曲力的作用位置為距離銅始極片界面端1/4處(位置3)但板厚分別為2 mm、3.25 mm、4.5 mm的組合3、組合6、組合9，可以看出:組合3的剪應力值比組合6、組合9大，更有利于剝離，但撓度值也比較大。

因此，在鈦板強度允許的條件下，選擇較小的鈦板厚度，將力的作用位置設置在靠近界面端的位置會有利于剝離并延長鈦板的使用壽命。

3 結束語

本文分析了銅始極片與鈦種板結結合界面上的剪應力分布，并應用有限元方法研究了鈦種板厚度和撓曲力作用位置的變化對預剝離的影響。

研究結果表明:在銅始極片上，剪應力在界面端處達到最大值，在其他區域剪應力比較小，而且沒有出現突變，這也是在外力作用下始極片率先從界面端分離的原因。在鈦板強度允許的條件下，選擇較小的鈦板厚度，將力的作用位置設置在靠近界面端的位置會有利于剝離，并且能減小鈦種板和始極片的撓曲變形，延長鈦板的使用壽命，減少后續始極片的矯平工作量。