上海房地產價格的空間相關性及其影響因素分析

文/王艷茹

一、引言

房地產業是國民經濟的基礎性產業，房地產價格的影響因素是國內外很多學者研究的重點。大量研究表明，房地產價格受市場需求、供給、容量和外部因素等影響，而各個地區之間的房地產價格也是相互依賴的，將空間相關性作為房地產價格研究的一項影響因素,可以為空間分析一定區域范圍內的房地產價格提供更加有效的依據。

上海作為直轄市、國家中心城市，是長江經濟帶的龍頭城市，中國的經濟、交通、科技、工業、金融、貿易、會展和航運中心。2015年10月，國務院批復原閘北、靜安兩區“撤二建一”，設立新的靜安區。目前，上海市轄黃浦、徐匯、長寧、靜安、普陀、虹口、楊浦、閔行、寶山、嘉定、浦東新區、金山、松江、青浦、奉賢、崇明16個市轄區。本文數據來源于《上海統計年鑒2016》及中原地產研究中心、搜狐焦點等。在統計年鑒相關指標和房地產價格數據查找中，大部分數據還是按17個市轄區劃分，所以本文在分析中將上海市靜安區分為原靜安區和原閘北區。

二、研究方法

本文運用探索性空間數據分析方法，多元線性回歸模型等方法，研究上海市各區房地產價格的空間相互依賴性及房地產價格的影響因素。

（一）空間自相關

空間自相關是指同一種屬性在不同的空間位置上的相關性，空間位置越是鄰近，屬性越趨向相同，空間現象越相似。空間自相關分析可以檢驗研究區域內各相鄰地區的集聚、分散性質，研究各區是相互獨立狀態還是呈隨機分布狀態，進而從空間異質性和關聯性方面測度各區房地產價格的空間分異格局和結構特征。為進行上海各區房地產價格的空間聯系狀況分析，本文基于ARCGIS10.3與GEODA1.8.14等空間分析工具，利用探索性空間分析方法從全局自相關和局部自相關兩個角度分析其關聯的類型與程度。

在空間自相關中，全局自相關可從整體上判斷市轄區的房地產價格是否存在集聚性，局部自相關可以定量分析市轄區房地產價格關聯的類型和程度。

全局自相關表達式為：

式中：xi、xj為市轄區i、j的房地產價格；

Wij為基于rook建立的空間權重矩陣；

n為區域內的17個市轄區；

I為Moran指數，在[-1，1]取值，大于0、等于0和小于0分別表示正相關、不相關和負相關，絕對值越大則表示相關性越強。

局部自相關表達式為：

式中：Ii表示局部自相關，即市轄區i受到市轄區j的影響。

局部自相關結果通常包括LISA集聚圖和Moran散點圖，Moran散點圖可以清晰地看出每個市轄區和其周邊相鄰市轄區房地產價格的相似或相依程度，包含四個象限，分別為高高、高低、低高、低低集聚四種類型。這四種局部空間關系的含義分別是:高高集聚表示中心市轄區與相鄰市轄區的房地產價格都較高，低低集聚則表示中心市轄區與相鄰市轄區的房地產價格都較低；這兩個象限內的市轄區房地產價格存在較強的空間正相關，即均質性。高低表示中心市轄區房地產價格較高，而其相鄰市轄區房地產價格較低，低高則表示中心市轄區房地產價格較低，而其相鄰市轄區房地產價格較高；這兩個象限內的市轄區存在較強的空間負相關，即異質性。

（二）多元線性回歸模型

在實際地理系統中，多個（多于兩個）要素之間存在著相互影響、相互關聯的情況。因此，多元地理回歸模型更具有普遍性的意義。

1.多元線性回歸模型的建立。多元線性回歸模型是描述因變量y如何依賴于自變量x1，x2，x3…xk和誤差項ε的方程，它的一般形式為：

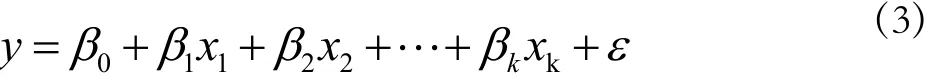
式中：β0為常數項，β1，β2…βk為模型的回歸系數，需要用樣本數據進行估計，表示在其他影響因素保持不變的情況下，xn變化一個單位時，因變量y變動的單位數。

ε為剩余殘差，與自變量無關，反映了除x1，x2，x3…xk與y的線性關系外的隨機因素對y的影響，表示的是不能由x1，x2，x3…xk與y的線性關系所解釋的變異性。

通過以上方式建立的線性回歸方程容易出現部分參數顯著性不高的問題，且自變量之間具有一定的多重共線性關系。所以本文又用逐步回歸法對模型進行一定的修正。逐步回歸，是在諸多自變量共同影響著同一因變量的關系中，判斷哪些自變量的影響是顯著的，哪些自變量的影響是不顯著的，然后從兩端分別將影響顯著的自變量選入和將影響不顯著的變量剔除。它既有剔除變量的運算，也有引入變量的運算，是目前應用較為廣泛的一種多元回歸方法。

2.多元線性回歸模型的顯著性檢驗。方程的顯著性檢驗，旨在對模型中被解釋變量與解釋變量之間的線性關系在總體上是否顯著作出推斷，即檢驗模型y=β0+β1x1+β2x2+…+βkxk+ε中的參數βi是否顯著不為0。可先提出如下原假設與備擇假設 ：H0:β1=β2=…=βk=0；H1:βi不全為 0。然后計算統計量F：

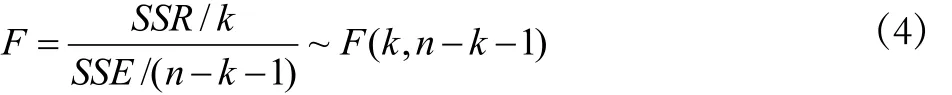
式中：k為分子自由度，且等于自變量個數，n-k-1為分母自由度。

給定顯著性水平α，可查詢F分布表得到臨界值Fα，由樣本求出統計量F的數值，若F＞Fα，則拒絕原假設，意味著肯定有解釋變量與y存在回歸關系。若F≤Fα，則不拒絕原假設。

三、實證研究

（一）上海各市轄區房地產價格空間自相關分析

為進一步了解上海各市轄區房地產價格的時空分異狀況，對各市轄區的房地產價格進行空間自相關分析，通過Moran’s I指數分析上海各市轄區房地產價格在時空上的差異。

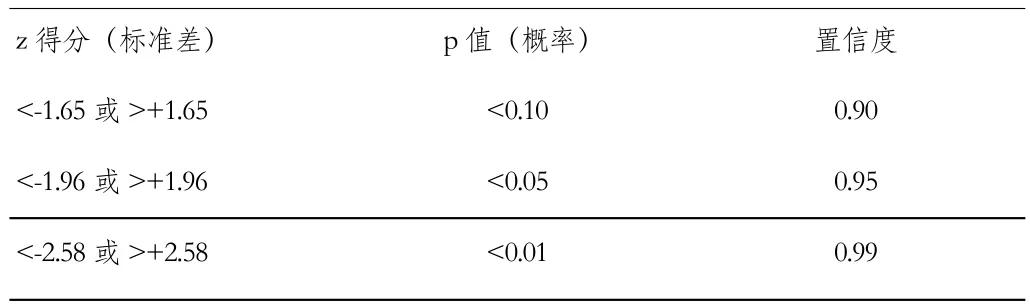
表1 不同置信度水平下的臨界p值與臨界z得分

表1為不同置信度下的臨界p值與臨界z得分，p值表示所觀測到的空間模式是由某一隨機過程創建而成的概率。z得分表示標準差的倍數。在置信度為0.90下，z得分值如果在[-1.65，1.65]之間，則觀測值在空間上表現為獨立隨機分布；z得分值大于1.65且顯著時，相似觀察值在空間上表現為集聚分布（高值或低值），小于-1.65且顯著時，相似觀測值在空間上趨于分散分布。

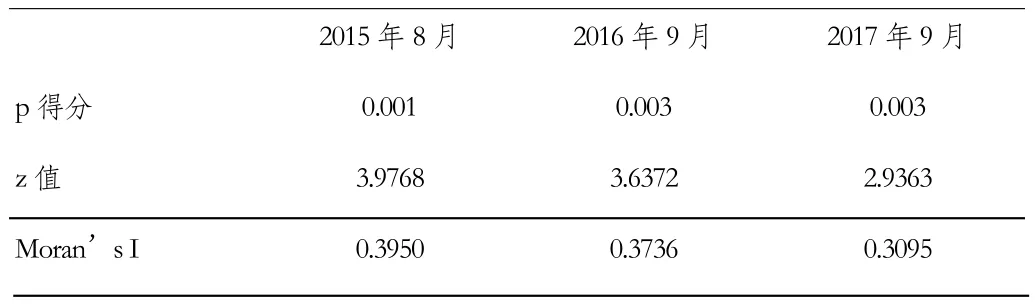
表2 上海各市轄區房地產價格Moran’s I指數

利用GEODA1.8.14軟件計算得出上海市房地產價格的全局空間自相關值(Moran’s I值)并檢驗其顯著性。表2給出了2015—2017年上海市各市轄區房地產價格的Moran’s I值及p值。由表2可知，研究期間，上海各市轄區房地產價格Moran’s I指數為正數，數值在0.20—0.39之間，表明上海各市轄區房地產價格具有空間正相關性，這顯示上海市房地產價格的分布呈現了空間上的聚集，即較高房價地區的周邊地區房價也較高，而較低房價地區的周邊地區房價也較低。p值小于0.01，說明這份數據隨機生成的概論只有1%（99%的置信度），z得分大于2.93，說明呈明顯的聚類特征。因此可對結果作進一步分析。

Moran’s I指數和Moran散點圖僅能反映出區域房地產價格整體空間的協同及集聚特征，無法反映出個體單元的房地產價格集聚及分散特征，因此通過LISA集聚圖能更好地解釋個體經濟之間聯系強度的集聚性和異質性。為了進一步揭示上海各市轄區房地產價格的空間自相關，筆者在GEODA1.8.14軟件和ARCGIS10.3中繪制了LISA集聚圖。

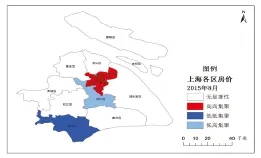
圖1 2015年8月年上海各市轄區房地產價格局部自相關LISA圖

圖1反映出研究時限內上海各市轄區房地產價格局部自相關特征，黃浦區、徐匯區、長寧區、靜安區、普陀區、閘北區、虹口區、楊浦區為高高集聚狀態，說明其與周邊市轄區的房地產價格均較高。閔行區在2015年8月屬于低高集聚狀態，即它的房地產價格比周邊市轄區低，因為閔行區距離中心市轄區距離較近，而房地產價格卻有一定差距，所以呈現圖中所示的集聚狀態。金山區處于低低集聚狀態，說明其與周邊城市的房地產價格均較低，其他大多數市轄區為無顯著性差距狀態，松江區、奉賢區等市轄區的房地產價格也不高，但因為其周邊既有房地產價格較高的市轄區，也有房地產價格較低的市轄區，所以呈現無顯著性差距狀態。

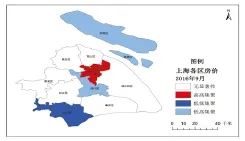
圖2 2016年9月上海各市轄區房地產價格局部自相關LISA圖

由圖2可知，2016年上海市處于高高集聚和低低集聚狀態的各市轄區房地產價格集聚狀態并未發生明顯變化，崇明區從無顯著性差距狀態變為低低集聚狀態。

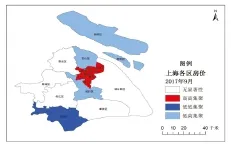
圖3 2017年9月上海各市轄區房地產價格局部自相關LISA圖

由圖3可知，2017年上海市處于不同狀態的市轄區房地產價格局部自相關變化不明顯，處于高高集聚和低低集聚狀態的各市轄區集聚狀態仍未發生明顯的變化，低高集聚狀態增加了寶山區。

由圖可知，在研究時限內，處于高高集聚狀態的市轄區為黃浦區、靜安區等中心市轄區，而一直處于低低集聚的市轄區則只有寶山區，處于低高集聚狀態的市轄區由2015年的閔行區增加到了2017年的三個市轄區，其他大多數城區則處于無顯著性差距狀態，主要原因是研究時限內各市轄區房地產價格不同，中心市轄區經濟發展水平較高，而寶山等市轄區由于受到地理位置的影響，經濟發展較為落后，房地產價格較低。從圖中可以看出，一個市轄區的房地產價格的確會受周邊地區房地產價格的影響。處于上海市中心市轄區的房地產價格受周圍地區的房地產價格的影響最大，而處于上海市相對邊緣地區的市轄區房地產價格受中心市轄區房價的影響程度小，相互之間則有一定的影響。

（二）房地產價格的變化規律及差異分析

通過分析上海各市轄區房地產價格的差異指數可得出其變化規律。

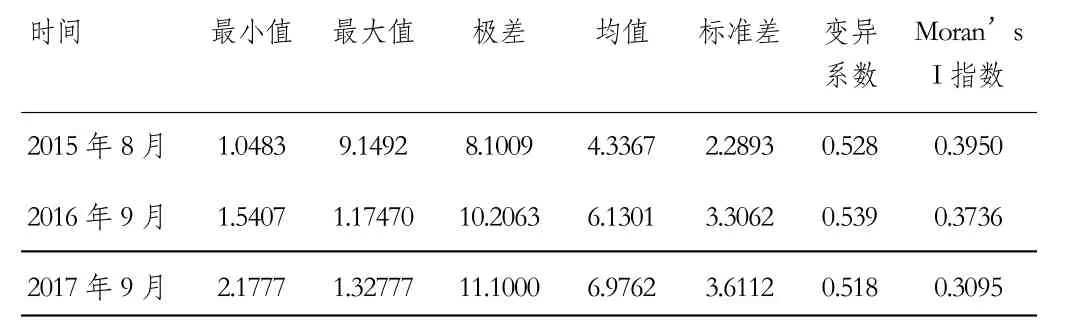
表3 2015—2017年上海各市轄區房地產價格差異指數

從表3可得：

1.上海市房地產價格最高的節點和最低的節點有一定差別，極化現象明顯。房地產價格平均值呈現不斷增大的趨勢，說明上海市房地產價格明顯升高。房地產價格極差從2015年8月的8.1009變為2017年8月的11.1000，造成這種差異增大現象的原因是最大值的增加值要大于最小值的增加值。變異系數也在不斷縮小，但并不明顯，說明上海市各市轄區房地產價格趨向均衡發展，但并非特別顯著。

2.由全局Moran’s I指數的變化可知，上海各市轄區房地產價格的空間自相關數值逐漸減小，說明在上海范圍內各市轄區之間的房地產價格依賴程度呈現減弱的趨勢，但仍然有著很大的空間自相關性。

（三）房地產價格影響因素研究

1.研究變量設定。房地產價格的影響變量眾多，可分為供給和需求兩個方面，具體可細分為經濟因素、政治因素、自然環境因素等。但因為數據收集和處理的難度，建立模型有較大的困難，很難考慮周全。本文在已有文獻的基礎上，考慮了代表性和可操作性，對變量進行了取舍和分類，如表4所列示。

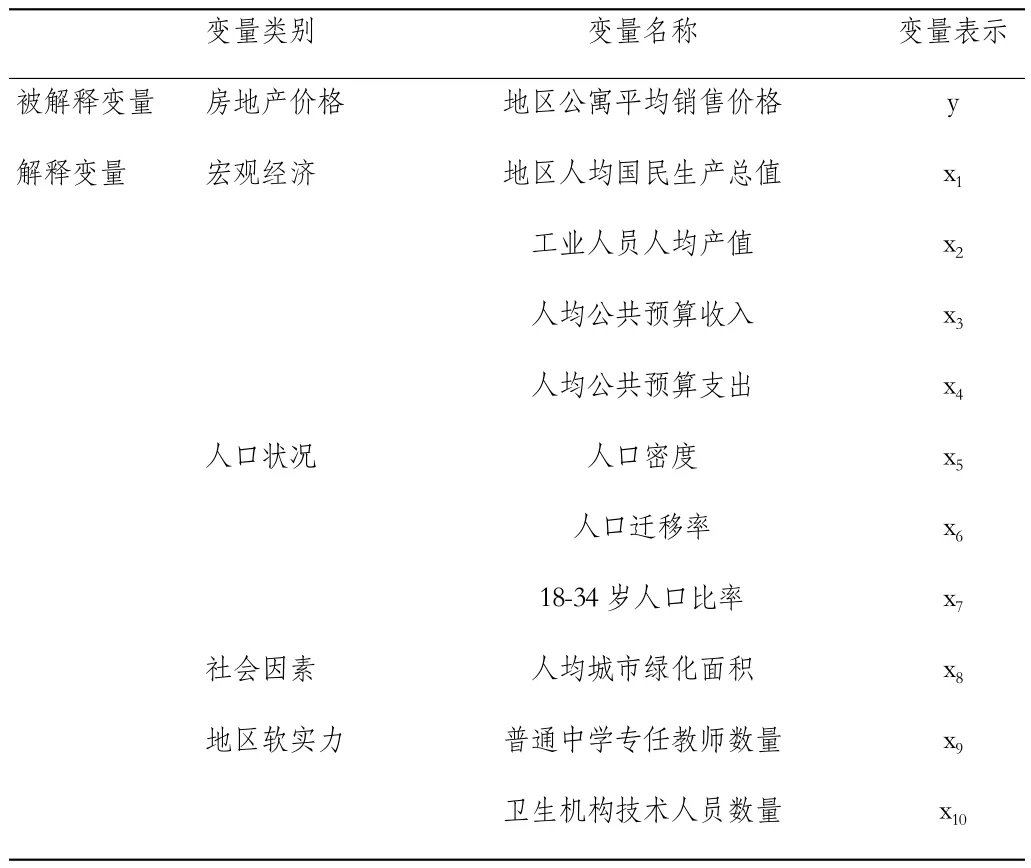
表4 上海各市轄區房地產價格變量設定

2.數據處理。本文利用MATLAB軟件編程，通過多元線性回歸模型（alpha=0.05）對各解釋變量于房地產價格的影響進行了估計，得出了如表5的結果。

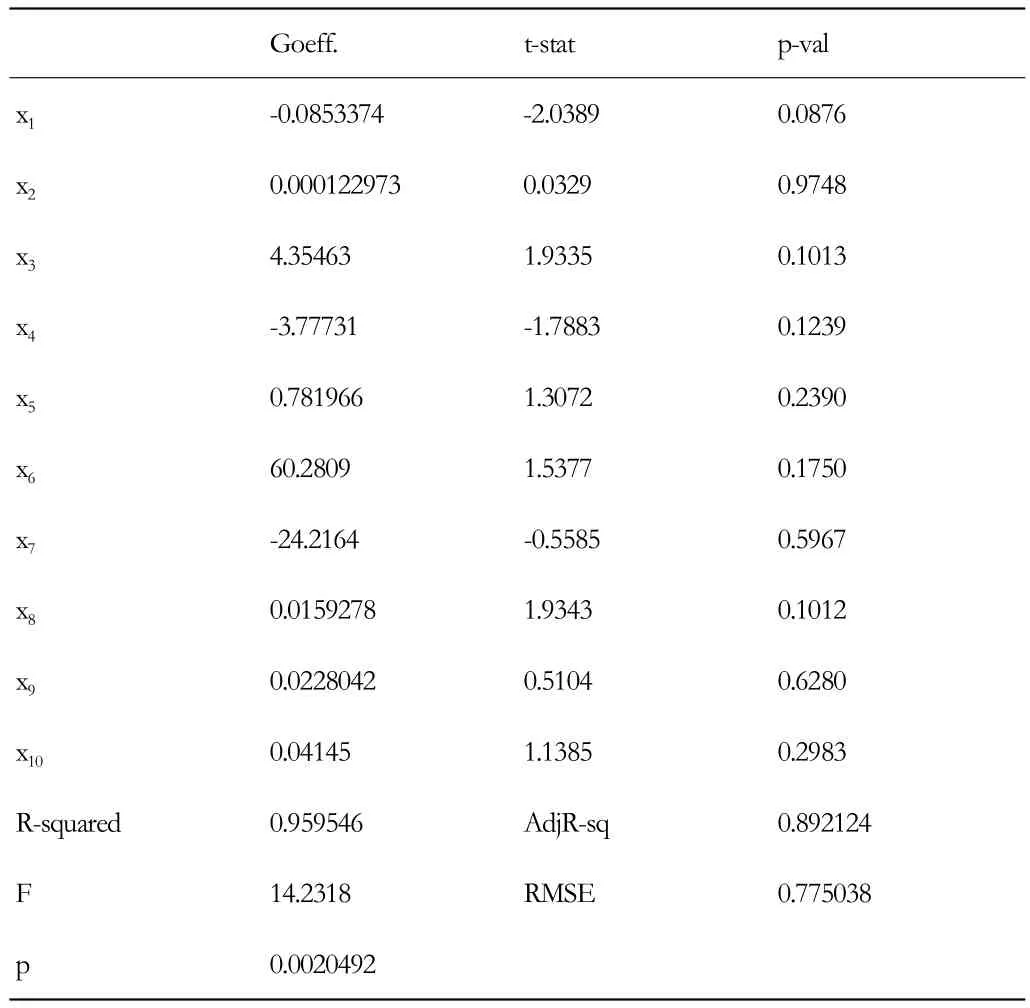
表5 上海各市轄區房地產價格影響因素計算結果

對獲得的結果進行分析得出：R2=0.9595，說明模型擬合較好。檢驗值F=14.2318＞F0.05(10,6)=4.06,符合要求，與顯著性概率相關的值p=0.00205＜0.05，這說明回歸方程是顯著的，但t檢驗的p值未全部通過，說明回歸系數是不顯著的，解釋變量間可能存在多重共線性，而且當解釋變量的個數與樣本容量比較接近時，也會導致變量之間的多重共線性。然而，由于信息資料相對匱乏，參數估計值很難得出，因此要通過MATLAB軟件對模型進行逐步回歸。經不斷剔除不顯著的變量后，回歸方程中錄用了原始變量x3、x4和 x5。

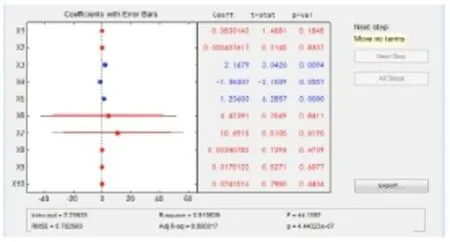
圖4 多元逐步回歸分析結果

模型評估參數分別為：

R2=0.910639，修正的 R2值 Rα2=0.890017，F 檢驗值＝44.1592，與顯著性概率相關的p值＝4.44323×10-7＜0.05，殘差均方RMST=0.782569，由圖可知，X3、X4、X5三個解釋變量擬合優度較高，F檢驗的p值接近于0，即總體回歸方程顯著，每個解釋變量都通過了t檢驗且經濟意義均合理，最后得到最優的回歸方程：

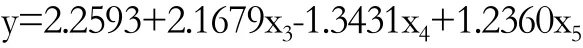
3.模型結果解釋。在最初的設定中，影響房價的因素共10個，但經過建立模型并進行顯著性檢驗后只保留了3個解釋變量。從運行結果看，保留的3個變量對房價的影響情況各不相同。

（1）從公共財政預算收入看，其系數是2.1679，說明公共財政預算收入與房價呈正相關關系，即公共財政預算收入越高,房價越高；反之，公共財政預算收入越低，房價越低。

（2）就公共財政預算支出而言，其系數是-1.3431，說明公共財政預算支出與房價呈負相關關系，即：公共財政預算支出越低房價越高；反之，公共財政預算收入越高房價越低。

（3）從人口密度看，其系數是1.2360，說明人口密度與房價呈正相關關系，即：人口密度越高，房價越高；反之亦然。

從回歸結果看，房價與公共財政預算收入、公共財政預算支出、人口密度這3個解釋變量存在很大關系，而其他解釋變量對房地產價格的影響可能不明顯或沒有影響，也可能是這些變量與前面的3個變量中的某些變量存在線性相關關系。從變量類別看，上海各市轄區房地產價格主要受宏觀經濟的影響，也會受到人口狀況影響，而地區軟實力對上海各市轄區的房地產價格影響不明顯，其原因是該地區的軟實力并不是孤立于硬實力之外而存在的，它們之間相互作用、彼此依賴。硬實力在為軟實力提供物質基礎的同時，也會依賴軟實力的促進作用。因此，硬實力強大的市轄區，其軟實力也一般具有良好的發展狀況，它們之間也存在著內生關系，所以會影響到模型結果。

四、結論

在研究時限內，上海各市轄區房地產價格不同，中心市轄區經濟發展水平較高，處于高高集聚狀態的市轄區包括黃浦區，靜安區等，各區房地產價格存在均質性；而一直處于低低集聚的市轄區則只有寶山區，寶山區由于受到地理位置的影響，其經濟發展和中心市轄區相比較為落后，房地產價格較低；低高集聚狀態的市轄區由2015年的閔行區增加到了2017年的3個市轄區，低高集聚狀態說明其周邊市轄區的房地產價格要高于自身的房地產價格，各區之間的房地產價格存在異質性，但是中心城區和郊區之間有很強的空間相關性。分析可知：一個市轄區的房地產價格的確會受周邊地區房地產價格的影響，處于上海市中心市轄區的房地產價格受周圍地區的房地產價格的影響最大，而處于上海市相對邊緣地區的市轄區房地產價格受中心市轄區房價的影響較小，但相互之間的房地產價格仍有較強的空間相關性。

在最初的房地產影響因素設定中，選擇的解釋變量共10個，但經過建立模型并進行顯著性檢驗后只保留了3個解釋變量。這說明上海各市轄區的房地產價格會受宏觀經濟的影響，但是依賴性一般。經分析發現，上海市房地產，除用于自住房外，還具有投資和商用的用途，有著很大的投資空間。近年來的價格上漲刺激了居民的購房意愿，也加快了投機者的步伐，從而使房地產價格進一步上漲，并產生了各市轄區之間的聯動效應，而降低了房地產價格對于宏觀經濟和社會因素的依賴程度。因此，在制定房地產調控政策時，應考慮房價的空間相關性，以控制房價的過快增長。