應急多跳無線網絡中的移動性研究?

張康榮 林基明 鄭 霖

（桂林電子科技大學信息與通信工程學院 桂林 541004）

1 引言

在應急的移動多跳無線網絡中，每個節點可能有幾個相鄰節點［1］。網絡中的節點必須通過允許并發傳輸和調整傳輸功率來決定最優的通信鏈路。而選擇用于建立鏈路的鄰居節點子集則是多跳網絡拓撲控制的主要目標［2～3］。

已有文獻基于同時滿足最優傳輸范圍和減少干擾對多跳網絡的拓撲控制進行了研究。研究成果表明較低傳輸功率的移動節點將導致網絡被分割，而較高傳輸功率的移動節點又通常會引起通信干擾，影響整體網絡容量［4～5］。因此需要對移動節點的拓撲連接進行必要控制。目前在拓撲控制中的大多數研究都沒有考慮到節點遷移，而是使用了一個用于網絡分析的靜態拓撲模型［6］。

文獻［7］中提出了一種基于方向信息的多跳無線網絡的分布式拓撲控制算法。該算法基于相鄰節點進行了傳輸功率的優化控制，降低了干擾，提高了可靠性。但是該算法并沒有解決網絡拓撲控制的問題。文獻［8］針對網絡中的每個節點根據局部鄰域和信道傳播模型信息計算出了強連通的拓撲。文獻［9］對靜態網絡拓撲控制算法進行了改進，使其能夠適應移動。文獻［10］提出了鏈接信息無拓撲（LINT），LINT算法利用節點度信息自適應地調整傳輸范圍，保持了靜態網絡中的連通性和雙連接性，但是該算法不能有效對節點的傳輸功率進行調節。

基于上述問題，本文提出一個提高應急多跳無線網絡的接入移動節點的能力的方法。首先針對節點遷移導致網絡拓撲動態變化的問題，通過利用非隨機移動模式，使得每個節點都可以預測鄰域拓撲的未來狀態，從而達到每個鄰居所需的最小傳輸能力。其次基于單跳鄰居的估計最小功率信息的最優傳輸功率選擇產生具有較強抗干擾性能的網絡拓撲。這種網絡拓撲結構是通過多跳通信保持連通性并因此保持網絡的整體覆蓋區域的拓撲結構。最后通過仿真測試對所提出的算法在保持有效傳輸功率的同時是否能夠可靠保持移動節點的連通性進行驗證。

2 基于移動節點感知的拓撲控制思路

基于移動節點感知的拓撲控制算法分為兩個步驟。首先，每個節點通過最大傳輸功率（Pmax）發送HELLO數據包，以了解鄰居拓撲的未來狀態。信息包包含節點的預測位置，以及在稍后的某個時間點與它的單跳鄰居通信所需的最小傳輸能力列表［11～12］。其次，每個節點選擇一個最優的功率級（Poptimal），這樣就可以通過一個要求更低的傳輸功率級來達到要求更高的傳輸功率的鄰居［13～14］。

算法主要思路如圖1所示。

圖1 拓撲控制算法主要過程

在圖1（a）中，描繪了在某個任意時刻（t0）的初始拓撲結構。此時HELLO數據包以最大的發射功率在鄰居之間交換。圖1（b）顯示了節點在時間（t0+α）的預測未來位置。節點5、4、3和2可以直接相互到達。圖1（c）表示了傳輸功率調整后的拓撲結構。其中每個節點調整了到達其鄰居所需的功率，以保持其連通性。例如，節點2計算節點5、4、3和1所需的功率，并依據計算結構建立了與節點3和1的鏈路。

3 拓撲控制和最優功率算法

3.1 拓撲預測和傳輸功率計算

在t0時刻，每個節點計算在t0+α時刻到達下一跳鄰居所需的最小傳輸功率的列表。t0和t0+α分別表示當前時間和下一跳時間，其中α是以s為單位的單位時間增量。下面對最小傳輸功率列表的計算方法進行闡述。

一個節點用以下兩個方程來基于當前位置、速度和方向預測其的未來位置：

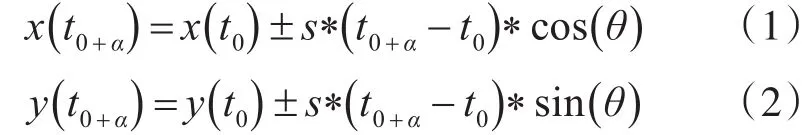
其中（x(t0+α)，y(t0+α)）表示一個節點在 t0+α時刻的位置，s是以某個最大值為界的當前速度，θ是節點的移動方向。

接下來，使用式（3）計算其與下一跳鄰居在t0+α時刻的距離。假設有兩個相鄰節點，即節點A和節點B，則：

最后，我們可以利用雙射線地面路徑損耗模型來預測基于無線傳播模型的任意兩個節點間隔距離上的平均信號強度Pr：

假設發射功率Pt和節點A、節點B之間的預測距離d( )t0+αAB是已知的，則使用式（4）可以計算出節點A與節點B之間的所需的最小傳輸功率。

3.2 最佳功率選擇

在接收HELLO數據包時，每個節點對拓撲映射進行預測，以確定與下一跳鄰居進行連接所需的最小傳輸功率。每個節點通過維護兩個數據結構來構造這個拓撲映射：1）局部視圖列表L包含兩個字段：下一跳鄰居的標識和最小的功率；2）擴展視圖列表E包括下一跳鄰居的標識、下兩跳鄰居的標識和估計的傳輸功率［15～16］。

算法利用局部視圖和擴展視圖列表，選擇了一個最優的功率Poptimal，這樣就可以通過一個中間鄰居節點來達到要求更高傳輸功率的鄰居。通過比較節點自身的傳輸功率和最近鄰的傳輸功率，實現了對Poptimal的選擇。如果最近的鄰居不覆蓋遠處的鄰居，算法會搜索另一個具有較高傳輸能力的鄰居，這樣所有鄰居之間的連通性就會被保留。尋找最優功率的算法流程如圖2所示。

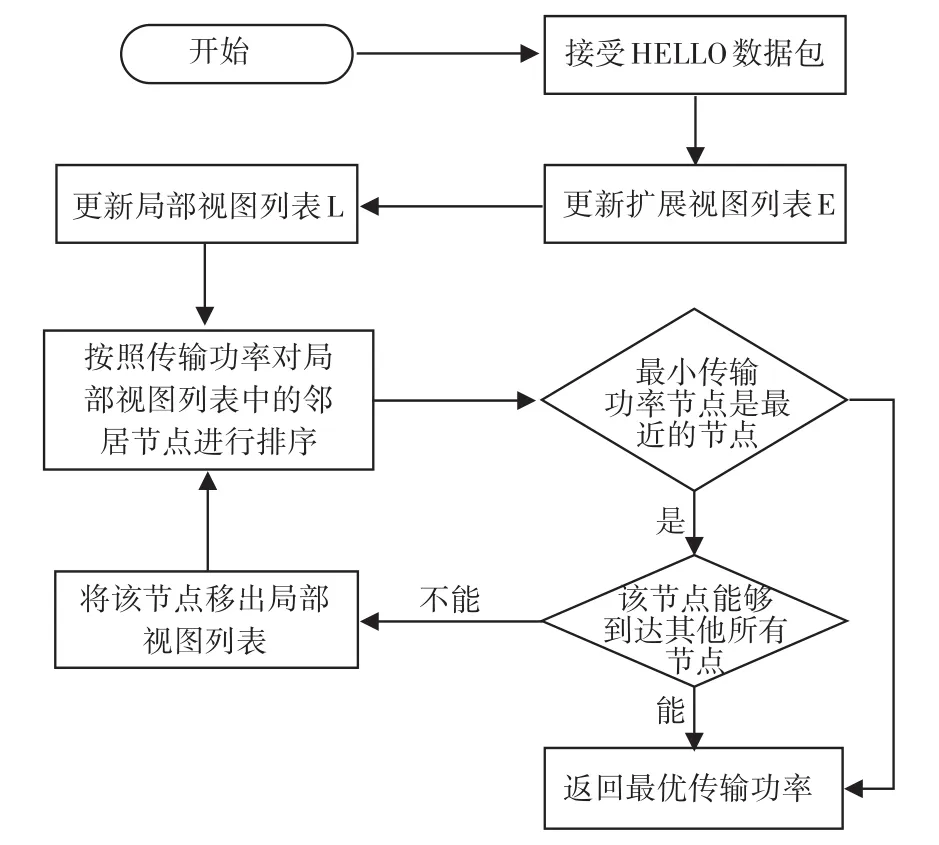
圖2 最優功率算法

一個基于最大傳輸功率的拓撲以及基于所提出的最優功率選擇算法構建的傳輸拓撲網絡的示例如圖3所示。

圖3 最優功率算法的效果

圖3中示例中基于二維地面反射模型在512×512m2區域上均勻分布的25個節點。圖3（a）描述了最大功率（18dBm）的拓撲結構，其近似傳輸距離為170m，即在沒有拓撲控制的情況下，每個節點的鄰居密度平均為8.08。圖3（b）是基于最優功率構建的拓撲控制網絡，其平均傳輸功率為12.07dBm，平均鄰域密度為4.88，因此在保持網絡連通性的前提下，該拓撲具有較低的局部鄰域密度和傳輸功率。顯然，圖2（b）所示拓撲網絡中的節點需要更少的傳輸功率。

4 仿真驗證

使用網絡模擬器NS2實現本文上述算法，并將本文算法與純洪泛算法（無發射功率控制）和局部信息無拓撲算法（LINT）進行比較。

洪水算法使用默認的傳輸功率級（即24.5 dBm）。另一方面，在節點度的基礎上進行傳輸功率調整。如果鄰居的數量少于6個，我們就會在全功率下運行LINT算法，隨著節點度的增加逐漸減少傳輸功率。移動節點被設置為有6個功率級，分別為 24dBm、21dBm、18dBm、13dBm、7dBm和-3dBm，這些功率級分別對應250m、210m、170m、130m、90m和50m的傳輸距離。表1總結了NS2中使用的所有參數的值。

表1 網絡模擬器NS2的參數設置

利用兩種非隨機網絡遷移模型，即確定性和半確定性的移動模型。1）在確定性遷移模型中，節點運動的偏差設置為零。2）在半確定移動模型中，偏差從-15°變化到+15°，因此節點運動在30°的柱狀寬度上變化。基于對CMU版本的NS2程序的修改，以生成仿真實驗的模擬場景。

4.1 仿真環境

在仿真模型中，節點被隨機放置在1000×1000m2的網格中。所有節點從1m/s移動到最大速度為20m/s，暫停時間設置為0。整個模擬持續時間為300s。在仿真實驗中，網絡大小從50個增加到150個，每增加25個節點。在性能評估中使用了以下指標：1）平均開銷，定義為每個節點每個數據傳輸接收的數據包的數量。2）平均傳輸功率，為總傳輸功率與網絡大小之比，其中，HELLO數據包僅包含在本文算法和LINT中。3）延遲，是指從源節點發送的數據和預期目的地接收到的數據之間的時間。

4.2 仿真結果

首先對網絡中廣播數據包的開銷進行監測。圖4（a）和（b）分別繪制了每個節點傳輸的平均開銷，并將節點的總數量作為確定的和半確定性移動模型的網絡大小的函數。其中圖4（a）是移動模型下的不同節點數量的無線網絡的廣播數據包的平均開銷；圖4（b）則是半移動模型下的平均開銷。

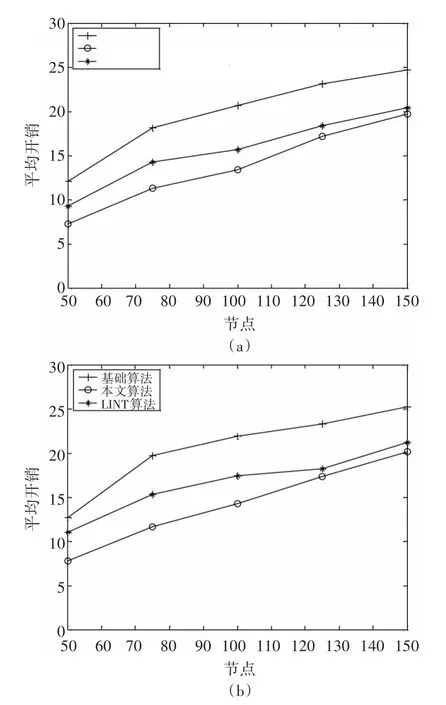
圖4 節點廣播的平均開銷對比

由圖4可知，本文算法的平均開銷始終低于基本算法和LINT算法。如前一節所述，應用拓撲控制的效果顯著降低了局部節點的平均密度，從而減少了相鄰節點轉發數據包的結果。這也有助于降低節點傳輸的功率，因為它通常會轉發較少數量的中間節點的包。LINT算法也是利用傳輸功率優化調整實現多跳無線網絡的拓撲控制，但是該算法只要監測到網絡連接性變差，節點就會轉向最大功率傳輸模式。因此兩種移動模型的開銷在較大規模的無線網絡中是接近的。

圖5（a）和（b）表示兩種移動模型的平均傳輸功率。其中圖5（a）是移動模型下的不同節點數量的無線網絡在保持節點連通性前提下的平均傳輸功率；圖5（b）則是半移動模型下的平均傳輸功率。

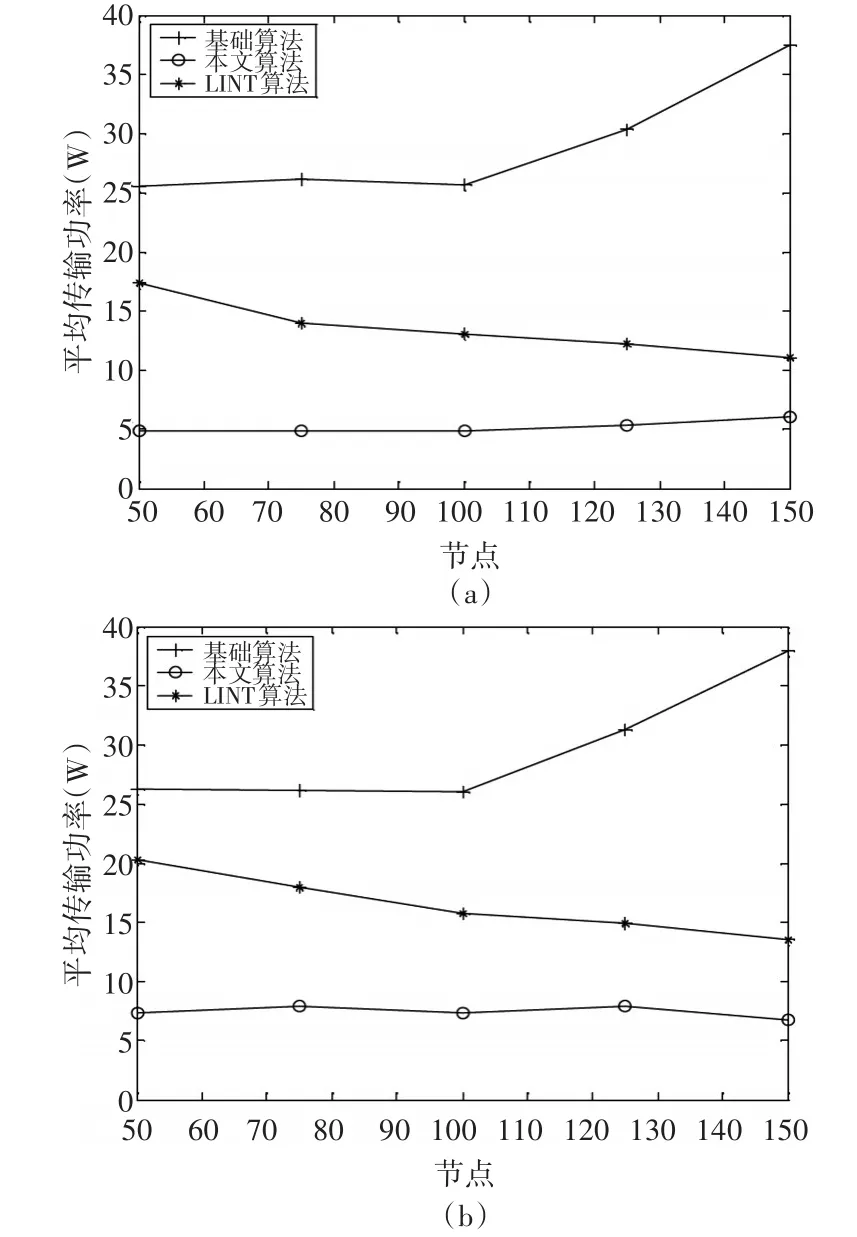
圖5 節點平均傳輸功率的對比

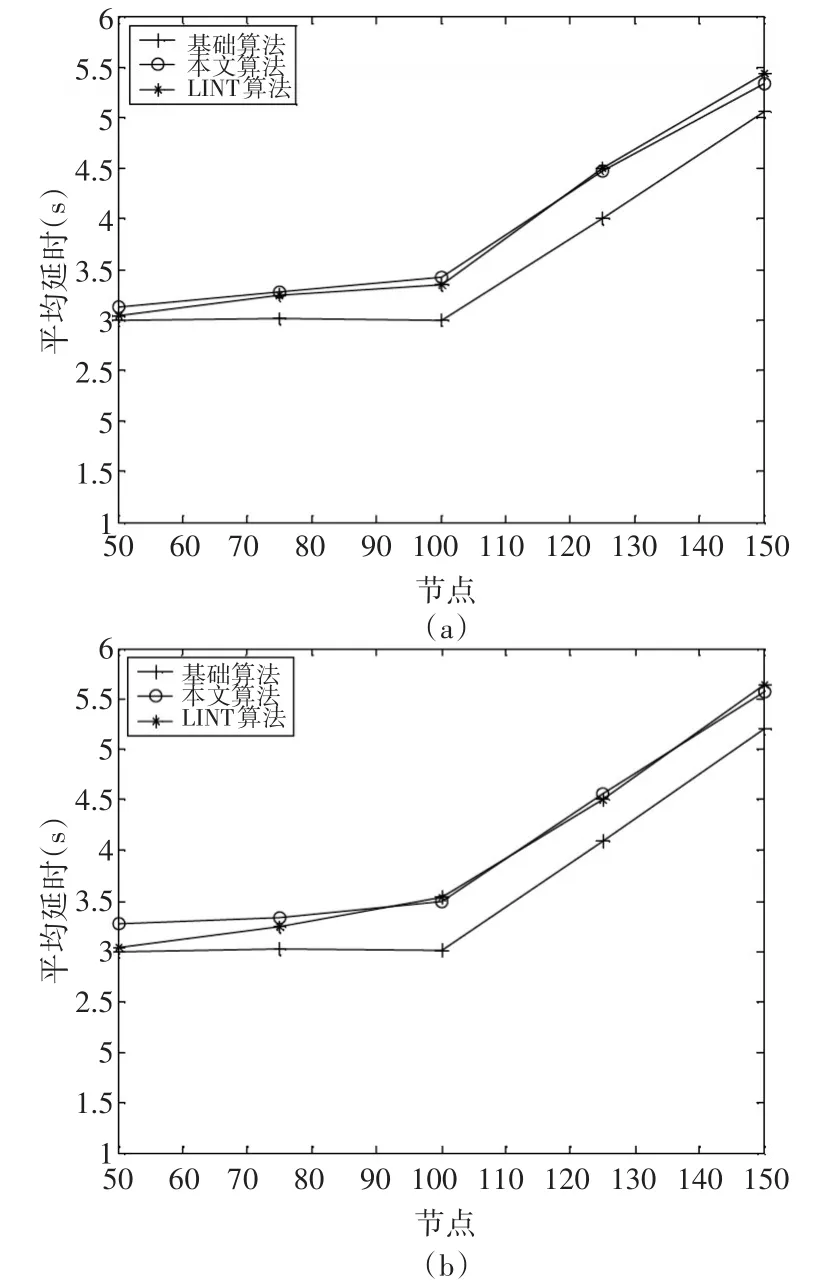
圖6 節點平均延時的對比

由圖5可知，本文所提出的算法能夠以最小的功率保持與在傳輸范圍邊界上的節點的連通性，而LINT在這種情況下運行在更高的傳輸功率級。對于較小的網絡，LINT必須增加一些孤立節點的能力。半確定性移動模型的功耗比確定性模型要高，這是為了補償相鄰節點的有限偏差。

圖6（a）和（b）為本文算法和其他算法分別在移動模型和半移動模型下的平均延遲。

由圖6可知，兩種移動模型的延時在所有的算法中都是相似的，并且在節點數量較少的網絡中本文算法的延時相對較高。在網絡密集的情況下，所有算法的延遲時間都相對較高。而在適度的流量負載下，非拓撲控制網絡的延時相對較低，因為與拓撲控制的網絡相比，在網絡中傳播數據包需要較少的跳數。

5 結語

本文提出了一種新的基于移動節點的拓撲控制算法。我們的方案利用非隨機節點移動模式來預測網絡拓撲的未來狀態。每個節點都運行一個分布式算法來估計成功地與每個鄰居進行通信所需的最小功耗。最后，節點將其傳輸功率調整到最優級以實現魯棒拓撲。仿真結果表明，本文算法支持節點間的多跳通信，以有效地利用有限的系統資源，如動態無線環境中的功率和帶寬。此外，由于我們的協議運行在一組離散的功率級別上，因此位置信息不需要非常精確。本文算法的基礎是一個單跳的HELLO數據包，因此網絡中的節點必須定期發送附加的鄰居信息的數據包，這對網絡負載會產生一定影響。