不同因素對艦船RCS特性的影響分析?

周 鈞黃 毅

（1.中國人民解放軍92941部隊 葫蘆島 125000）（2.中國船舶重工集團公司第七一〇研究所 宜昌 443003）

1 引言

雷達散射截面積是指物體目標對雷達發射波的反射截面積，是一個等效面積，它表征目標對電磁波的散射能力的強弱，雷達散射截面積的大小對后續雷達處理成像至關重要，是描述雷達探測目標信息的一個最重要、也是最基本的參數［1～4］。在實際的雷達探測系統中，海面的隨機起伏和測量環境的差異會嚴重影響艦船RCS的特性，對雷達的探測結果會產生一定的干擾偏差，性能下降［7，10～11］。文獻［1］研究了在海面的波浪影響下，艦船目標的RCS分布特性；文獻［2］研究了不同的海情以及蒸發波導對海面艦船RCS的影響；文獻［3］研究了海面浮油對雷達回波的影響；文獻［4］研究了對粗糙海面進行建模的方法；文獻［7］研究了不同的雷達波頻率、極化方式和入射角度對艦船目標RCS的影響；文獻［9］研究了三維復雜粗糙海面電磁散射建模的方法與特性分析，文獻［10］研究了隨機粗糙海面的建模與仿真。

通過對以上文獻分析，本文主要研究在粗糙海面背景影響的情況下，雷達入射波以不同的頻率，不同的極化方式以及不同的入射方向分別照射某大型艦船，并利用FDTD算法進行求解艦船的RCS，觀察以上各個因素對艦船RCS特性的影響。因此研究不同的影響因素對研究艦船RCS的特性計算分析具有現實意義。

2 相關理論

2.1 雷達散射截面積

雷達散射截面積定義為雷達入射波照射目標物體時，目標物體對入射波呈現散射的有效面積。當照射距離遠大于物體的實際尺寸時，我們認為入射波為平面波，功率密度是

因此RCS為σ的目標能夠截獲的功率為

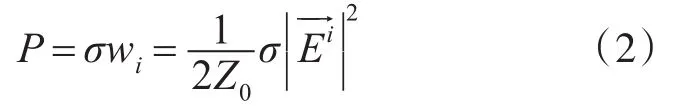
如果目標將這些功率各向同性地散射出去，則在距離為R的遠處，其散射功率密度為

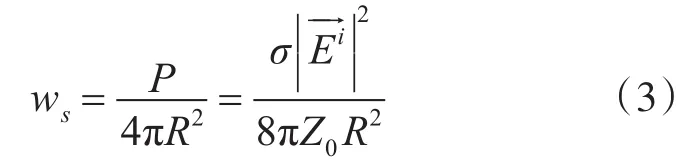
散射功率密度也可用散射場來表示：

由式（2）和式（3）可解出

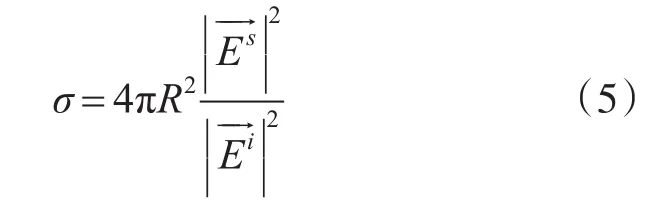
由于觀測距離R在遠場區，且入射波是平面波，所以式（5）可以嚴格地寫為

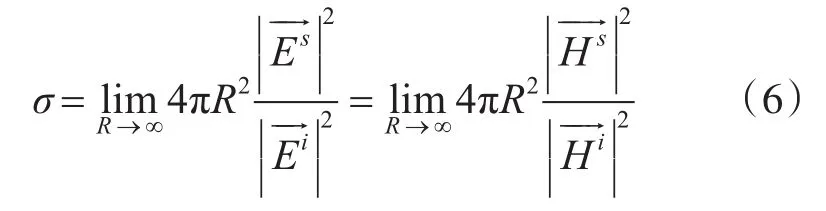
這就是雷達散射截面積最基本的理論定義式。

2.2 海面模擬建模

研究海面艦船RCS時，僅通過海水起伏的統計量模型，利用均方根、相關長度等參數不足以反映粗糙海面對目標艦船RCS的影響，因此需要對粗糙海面進行建模，海面模擬的方法主要包括統計模型和分形模型兩種方法。

本文研究蒙特卡洛的統計方法，并對粗糙海面進行建模。蒙特卡洛的主要思想是：首先將白噪聲進行傅里葉變換到頻域，然后在頻域利用海譜函數對其進行濾波，最后對濾波后的頻域函數再進行傅里葉反變換，即可得到海面的高度起伏函數［3，8］。蒙特卡洛統計方法也稱為線性濾波過程。

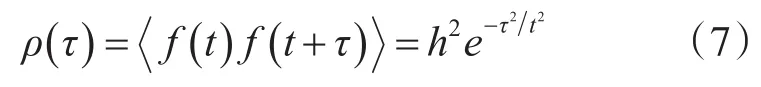
式中，f(t)為隨機粗糙面函數；h為海面的高度起伏函數；l代表自相關長度。根據自相關函數與功率譜的傅氏變換關系，可得自相關函數的功率譜：

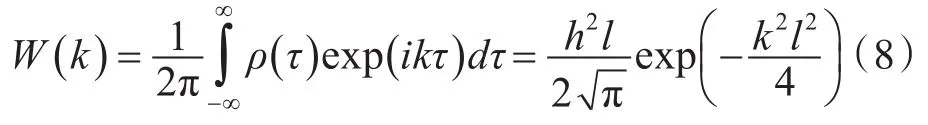
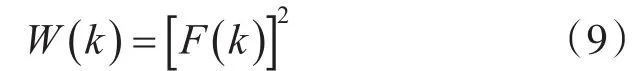
令

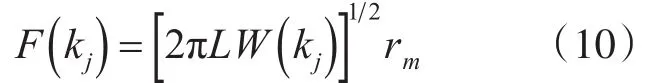
式中

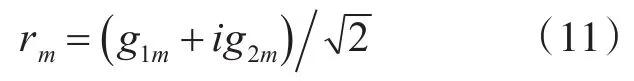
且復變量rm服從正態分布；代表兩組相互獨立的符合高斯分布的隨機數，為歸一化因子并且使的取值決定了海面的高度隨機起伏的輪廓線，我們這里只取粗糙面函數的實部作為研究對象。

根據式（2），我們選取Pierson-Moskowit譜來模擬粗糙面，也可以選取高斯譜來模擬，前者是表面風場帶來的海浪平面，對RCS的計算分析具有現實意義。表面譜參數方程如下：式中各參數變量代表的數值為為表面風場的平均速度，l為相關長度。

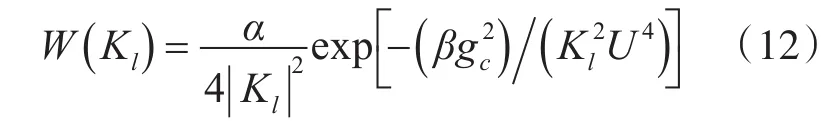
2.3 時域有限差分法

計算分析物體目標的RCS有兩種方法：精確解法和近似解法。

精確解法只針對簡單的情況而言，即當散射體的幾何形狀與某一可分離的坐標系相吻合時才是可行的。

然而在實際的電磁學中，實際應用中很難滿足精確解法的條件，因此人們以麥克斯韋方程組為基礎，提出了多種近似的方法進行求解，這些近似方法在復雜的幾何體上存在局限性，需要進行修改來解決復雜場合中的RCS問題。計算RCS的近似方法大致有以下幾種：物理光學伊、幾何光學、幾何繞射理論、物理繞射理論、矩量法以及時域有限差分法等理論，本文主要應用時域有限差分法。

時域有限差分法是一種研究電磁問題的時域數值方法，它在解決復雜外形、非均勻介質、時域、寬帶散射和輻射系統的電磁問題時具有獨特的優越性。其核心思想是直接在時問和空間域將Max?well方程進行離散的一種時域方法，是計算電磁學界中比較流行的算法，目前國外已有多種基于FDTD算法的電磁場計算的軟件：FEKO，XFDTD等，具有廣泛的應用性［5～6，8］。FDTD 算法不但具有節約運算和存儲空間、適合并行計算等優點，而且計算程序具有通用性，簡單直觀。

利用時域有限差分法進行計算分析艦船RCS特性時，必須對艦船進行建模。建模步驟：

1）部件拆分

首先對復雜的艦船散射體按照其幾何結構進行劃分，分解成單個部件然后進行處理，單個部件的拆分方式不同，目標的描述文件也會有差異。

2）幾何參數文件建立

然后根據平移的坐標系，對各個部件的幾何外形尺寸進行參數錄入，這樣對目標各個部件參數數據的讀取會很方便，最后對建立的幾何體進行平移到正確位置，利用布爾運算進行整體艦船組合。

3）FDTD剖分

根據上一步驟中各個部件的適當點坐標，對整個艦船進行FDTD剖分。剖分網格的大小與照射電磁波的波長的關系為：δ≤ λ 12，λ=c f，f為照射波頻率，c為自由空間波速，λ為照射波波長。由此可見波長越短，剖分網格越小，艦船表面被剖分的網格數就越多，計算仿真的時間也會越長。

3 仿真結果

最后，對海面上某大型艦船，在粗糙海面的影響下，雷達波分別以不同頻率、不同極化方式、不同入射角度對其進行RCS分布特性計算分析。

仿真參數：入射波以線極化方式照射，幅值1v/m，入射方向水平角30°，俯仰角 60°，圖1（a）～圖6（a）是在粗糙海面背景下計算分析的艦船RCS，圖1（b）～圖6（b）是只有艦船存在的情況下計算分析的艦船RCS。

圖1是頻率為100MHz的垂直極化入射波計算的 RCS，從圖 1（b）可以看出，水平方位為 45°時，RCS相對其他兩個方位更大，而圖1（a）則是在海面背景影響下仿真得到的RCS，可以看出海水的散射對艦船 RCS 的影響是嚴重的，在-30°～-60°艦船RCS大幅度增加。

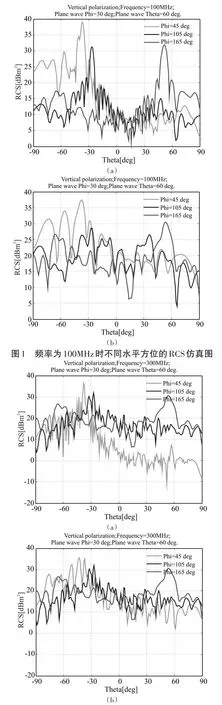
圖2 頻率為300MHz時不同水平方位的RCS仿真圖

圖2是頻率為300MHz的垂直極化入射波計算的RCS，圖2（b）與圖1（b）對比可以看出，隨著入射波頻率的增大，艦船RCS變化頻繁劇烈，圖2（a）與圖2（b）相比，同樣可以得到，海水對艦船RCS產生嚴重影響。

圖3是頻率為100MHz和300MHz的垂直極化入射波，100MHz的入射波產生的艦船RCS相對平緩。

圖4是頻率為100MHz的水平極化入射波照射得到的艦船RCS。

圖5是頻率為100MHz入射波分別以水平極化方式和垂直極化方式照射艦船計算的RCS，從圖中可以看出艦船的RCS大體走向相同，存在略微的差異。

圖6是在不同入射角時得到的RCS仿真圖，當入射角度變化時，海面對艦船的RCS影響很大。

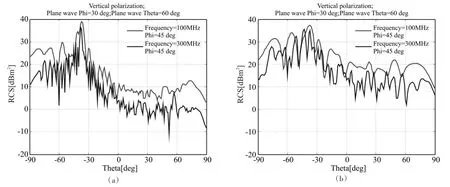
圖3 不同入射頻率的RCS仿真圖

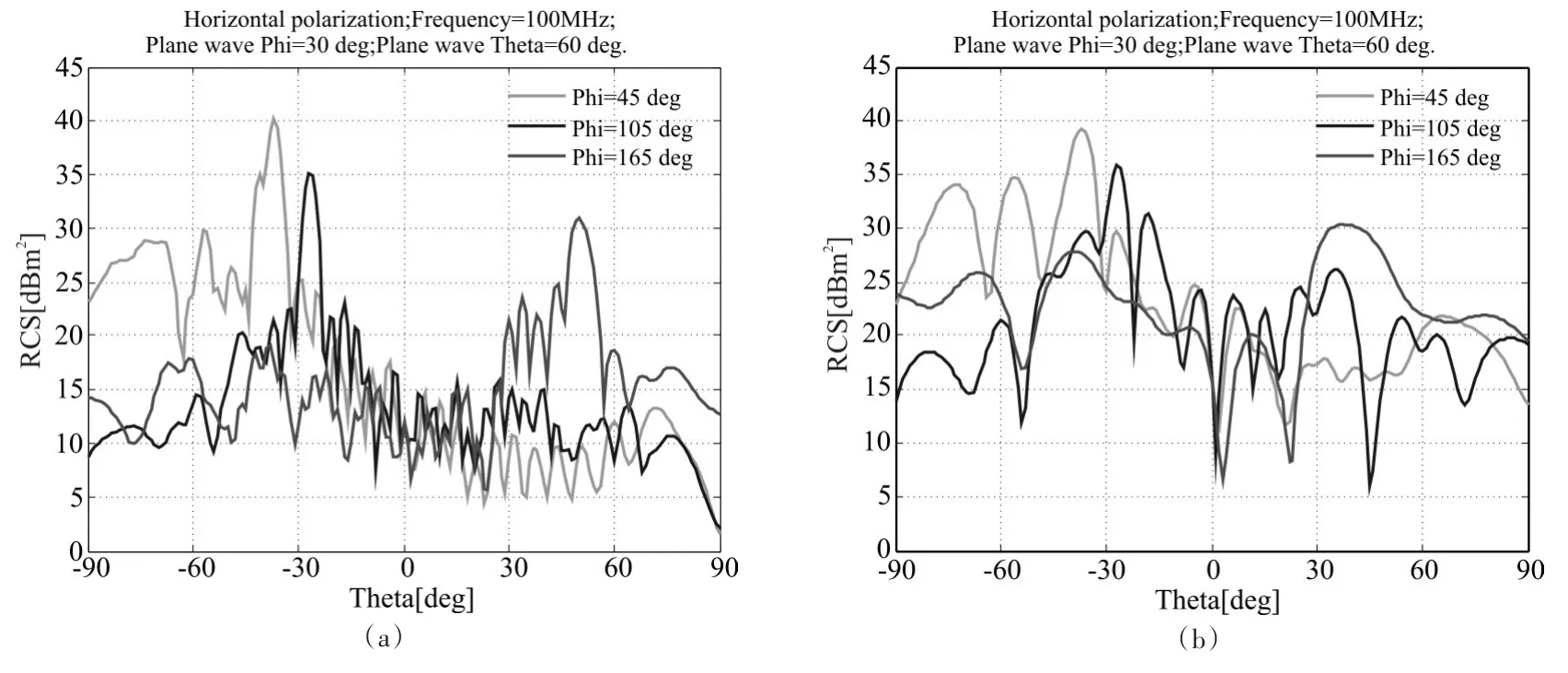
圖4 不同水平方位的RCS仿真圖

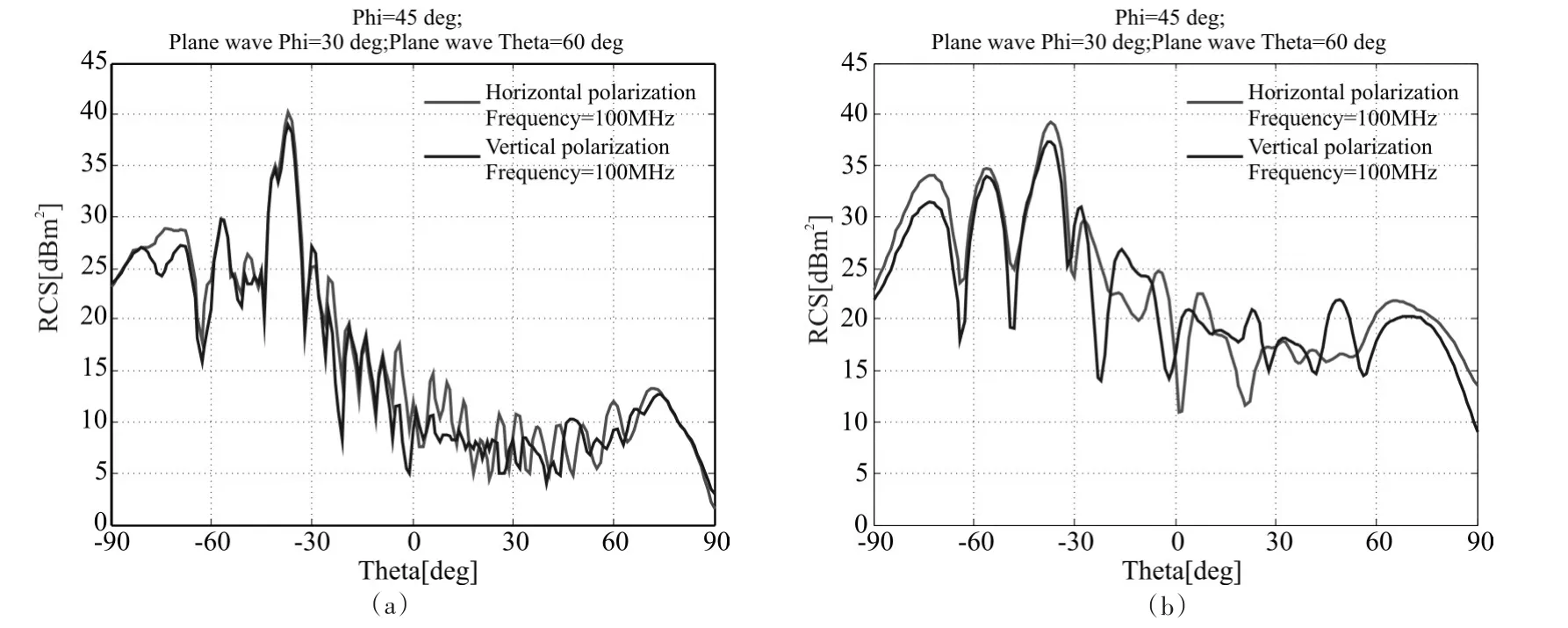
圖5 不同極化方式下的RCS仿真圖

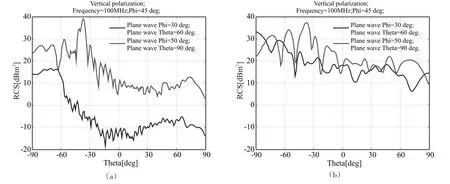
圖6 不同入射角時的RCS仿真圖

4 結語

本文以海上某大型艦船為例，研究了在粗糙海面的背景下某大型艦船的RCS特性，實際海洋的環境對艦船RCS影響很大。分析了粗糙海面的統計模型方法，選取了Pierson-Moskowit譜來模擬海面，討論了在不同極化方式，不同入射角，不同頻率時的艦船RCS，分別仿真了在有海面背景下的艦船RCS與無海面背景下的艦船RCS，得到了對比圖，水平極化與垂直極化對目標RCS幾乎影響不大。研究結果對海面偵測雷達提供了理論參考，具有實際意義。