基于卡爾曼濾波理論的質量數據評估方法研究?

嚴錦濤 陳硯橋 劉曉威

（海軍工程大學動力工程學院 武漢 430033）

1 引言

由于武器裝備應用環境的多樣性，使用、維修單位分布的廣泛性，數據來源涉及工作項目多，使用裝備質量數據主要為日常工作中所記錄產生的數據，表面繁雜且無序，使得部隊武器裝備質量數據具有鮮明的不確定性等特點，從而給裝備質量數據管理以及利用裝備質量數據進行的質量評估帶來了很大難度［1］。加之在裝備質量評估過程中，統計數據一般由于系統誤差、測量誤差等原因，數據波動大且難以找到典型的分布規律，定性因素與定量因素交織，正因如此，采用一種合適的數據評估方法用來評估質量數據是質量評估過程中最為重要且關鍵的步驟。

卡爾曼濾波理論一出現，就得到了軍界的高度重視，在宇航和軍備領域里，應用成果層出不窮。有關“阿波羅”登月計劃中的導航系統以及C-5A飛機的多模式導航系統等，都是卡爾曼濾波理論提出后早期成功應用的例子［2］。至今，凡是需要進行實時數據處理的場合，卡爾曼濾波一直占據主導地位。在海軍艦載指控系統、各種火控系統以及綜合導航系統中，應用卡爾曼濾波技術是其現代化水平的重要標志之一［3］。

本文提出基于卡爾曼濾波的質量數據不確定性評估方法，卡爾曼濾波是信號處理和控制理論中的一種標準方法［4～6］。所謂濾波，就是從受到噪聲污染的有限觀測信號中，提取出被觀測系統的參數或狀態，不確定性即體現在具有噪聲的污染，此處所說的噪聲污染其實指的是測量過程中存在的誤差，系統則是指裝備整體或是某一個部件。卡爾曼濾波是根據與被提取信號有關的觀測值去推斷或重構出最符合系統狀態真值的一個最優估計，因此，卡爾曼濾波本質是一種狀態的最優估計，并且是線性、無偏、誤差方差最小的一種最優估計，此處所稱的濾波與常規濾波具有完全不同的概念和含義，更多的是作為估計方法［3］。其基本思路圖如下。

圖1 卡爾曼濾波理論思路框圖

2 基本理論

對于線性系統數據評估使用基本卡爾曼濾波理論［7］

其中，F、A、C為可能隨著時間變化的系統模型矩陣，F為狀態轉移矩陣，C為觀測矩陣，A為干擾轉移矩陣，x(k)為狀態向量，y(k)為系統觀測或輸出向量，以及系統隨機干擾向量m(k)與已知的協方差矩陣Q(k)和隨機觀測誤差n(k)與已知的協方差矩陣R(k)。為便于表達與計算簡單，向量x的估計值用x^表示，同時假定A≡I，為單位矩陣，即把這些誤差看成是高斯白噪聲，也就是誤差跟前后時間是沒有關系的而且符合高斯分布。例如，艦上雷達跟蹤敵機運動時，雷達的跟蹤誤差一般可以認為與敵機的運動狀態無關，另外，系統的隨機干擾與系統初始狀態往往也是獨立的。

此處考慮狀態估計的目標是從系統模型矩陣和觀測值 y(k)中對x(k)的序列估計。在序列估計中，狀態向量x(k)的估計值及其協方差矩陣P(k)是由k-1時刻x(k-1)的估計值及其協方差矩陣P(k-1)和當前k時刻的系統觀測值 y(k)計算得出，當k=0的初始時刻，會給出一個初始的狀態向量初始值和初始協方差矩陣。

由文獻［7］相應的卡爾曼濾波基本方程為

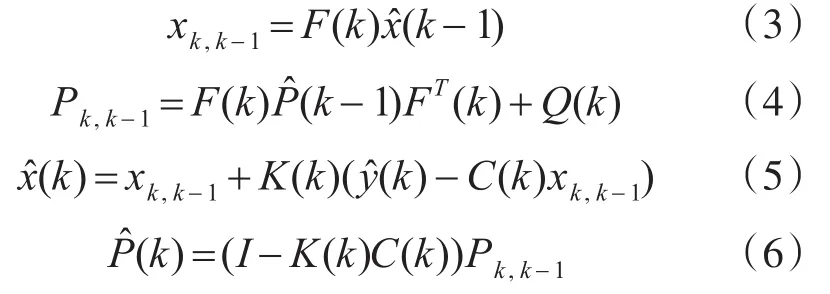
利用卡爾曼增益矩陣

其中，式（3）為一步最佳預測，式（4）為驗前方差陣，式（5）為濾波方程，式（6）為驗后方差陣。狀態方程式（1）為狀態預測提供了基礎，由于系統隨機干擾m(k)是白噪聲序列，而白噪聲序列是不相關的，其最佳估計只能是其均值。因此，由狀態方程式（1）和已知的x^(k-1)，可得到狀態向量的一步最佳預測 xk，k-1。

3 模型的建立

對于線性卡爾曼濾波理論的式（3）～（7），建立測量模型為

也可以表示為

其中

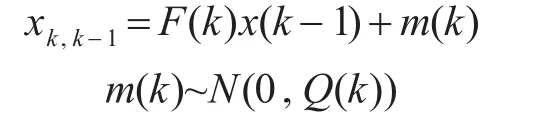
關于測量模型有以下兩種情形：已知的測量模型和未知的測量模型。為便于表達方便與計算簡便，本文主要研究基于已知的測量模型的卡爾曼濾波估計。

當系統模型是準確已知的，在式（9）中預測當前狀態估計的唯一不確定源是系統觀測向量y(k)，誤差m(k)和n(k)。與觀測向量 y(k)相關的不確定性由協方差矩陣R(k)給出，它代表了觀測瞬時k時刻的誤差協方差。在最簡單的情況下，誤差被認為是獨立的服從高斯分布的誤差（即白噪聲），同時已知分布的標準差。對于更復雜的帶有誤差的結構，可以使用矢量回歸（VAR）模型［8］。

假定與估計值x^(k-1)相關的協方差矩陣P(k-1)=Pk-1，k-1可以很有效地代表模型估計中的不確定性，存在多元正態分布：

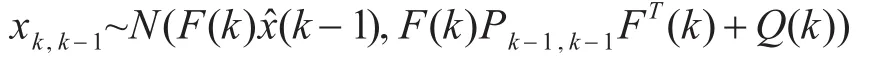
兩個輸入量都假定是獨立獲得的，這種情況下它們的聯合分布概率密度函數便為其各自概率密度函數的乘積。由于式（9）中的 xk，k-1和 y(k)的測量模型是線性的，且它們服從的分布是正態分布，通過測量模型可以對聯合概率密度函數進行計算分析，得出k時刻最佳估計為

和協方差矩陣

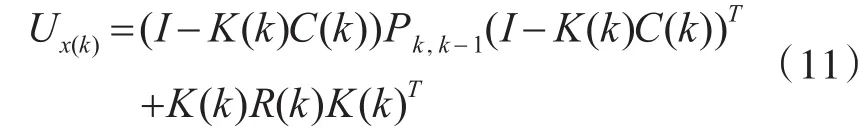
簡化結果為

4 實例分析

本文使用下例來說明對于質量數據的處理中卡爾曼濾波的不確定性評估。假設一個水箱在使用過程中滿足正弦曲線變化規律，無法直接通過觀察精確得出水箱的水位與振幅，并且在進行測量過程中由于儀器失準等外界因素的影響存在誤差［9］。此時假設存在關系式

初始的水位為L0=100cm，初始振幅為xs0=0.01cm，頻率θ=0.8Hz，導數為

所研究的考慮到誤差因素的水位與振幅測量值，目的是用來估計實際水位xl與振幅xs。在研究時間范圍內水箱系統水位與振幅的變化表述為如下

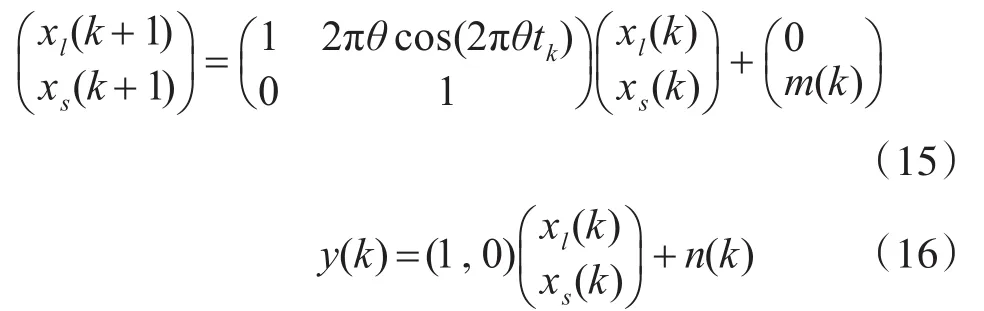
其中狀態和測量誤差滿足 m～N(0，τ2)和 n～N(0，σ2)［10］，標準差 τ=0.01和 σ=1.0 。

圖2表示存在誤差時隨時間推移的水箱系統在假設條件下的水位與振幅變化。可以看到在存在誤差情況下，隨著振幅的波動變化，水位的變化幅度值也在隨之變大變小具有隨機性，且變化不具有預見性。現實環境下，在未知實際水位與振幅時，只能通過測量估計得到水位與振幅，本文模擬了一個實際水位與振幅，比較實際水位與振幅和測量得到的水位與振幅的相近程度，目的是用來檢驗卡爾曼濾波的數據估計水平。

圖2 假設條件下系統的水位與振幅

由于測量系統（15）～（16）是具有服從正態分布誤差的線性模型，因此可以將線性卡爾曼濾波理論應用于數據評估［11］為

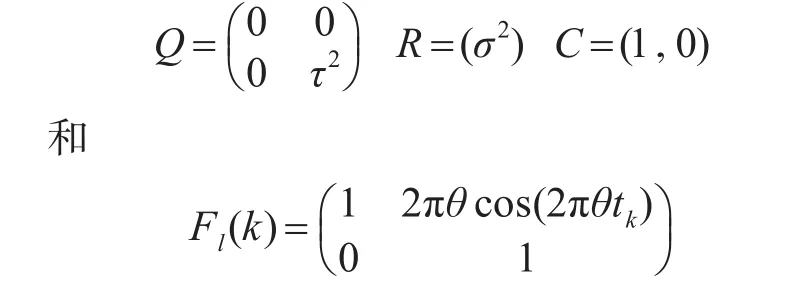
圖3為假設條件下系統利用卡爾曼濾波估計得出的測量水位與測量振幅，由圖可以看出，由于誤差的干擾，卡爾曼濾波方法不斷遞歸估計得出的水位與振幅和實際的水位與振幅產生了一定的偏差，無法呈現為較為直觀的線性狀態，但是大致變化具有一定的趨向性。

將模擬實際水位與振幅和估計得出的水位與振幅生成在一張圖中，結果如圖4所示。卡爾曼濾波估計得出的測量水位與振幅和模擬實際水位與振幅較為吻合。在某些時刻，模擬實際水位與測量水位圖形幾乎重疊一致，在測量區間內，線性整體走勢基本一致，估計精度較高。如果要求測量誤差方差進一步減小，估計精度將可以進一步改進。

圖3 卡爾曼濾波估計的測量水位與振幅

圖4 卡爾曼濾波估計結果與模擬系統對比圖

實際情況下，當已知系統由于誤差等因素的影響使常規測量失準時，無法評估誤差對數據的影響程度以及數據的具體變化。此時卡爾曼濾波方法可以很好的評估數據，并且在已知誤差服從的規律為高斯分布的前提下，多次對誤差遞歸得到最小方差無偏估計。利用Matlab仿真結果發現無論生成多少次圖形，誤差對圖形影響的情況不同，然而卡爾曼濾波都可以較為吻合的評估數據變化，效果依然很好。

綜上通過卡爾曼濾波理論的估計結果，總結卡爾曼濾波突出的優點，可歸納如下：

1）卡爾曼濾波是一套完整的遞推算法，特別適合于計算機處理，占內存少，運算速度快，適合實時處理。

2）估計精度高。它是目前已知的估計方法中最好的一種。

3）適應性強。不但適合處理單輸入、單輸出系統，也適合多輸入、多輸出系統；適合平穩或非平穩的隨機系統，時變過程，稍加推廣，也可用來次優估計非線性系統的狀態變量。

4）在得到狀態變量最優估計的同時，也可得到估計誤差的方差陣，可以作為估計精度的一種量度，便于在線監控濾波器的工作質量。

5 結語

卡爾曼濾波理論將被估計的數據看作是線性系統在服從高斯分布誤差作用下的輸出，并且在時間范圍內，線性系統的輸入、輸出關系由狀態方程和輸出方程給出，這種特點適用于多輸入、多輸出的估計問題［12］。將卡爾曼濾波方法用于質量數據評估減少了誤差對估計值的影響，因為如果測量誤差增大，濾波增益就應該取得小一些，以此減弱測量誤差對估計值的影響。

本文利用卡爾曼濾波理論實現一個簡單實例質量數據評估的方法——水箱水位與振幅問題。通過研究表明，卡爾曼濾波理論在質量數據評估方面具有較高的研究價值，當由于實際使用情況的特殊和限制因素，無法直觀得到裝備質量數據時，可以通過卡爾曼濾波理論用來估計裝備質量數據當前的大致狀態，并將估計精度提高到一定的程度上，便于使用者掌握和了解裝備的使用現狀，便于評估的進一步開展和進行。此外卡爾曼濾波和狀態評估的相關方法在許多領域得到了成功的應用，其按順序產生了對狀態向量的估計，并通過在估計中不斷更新的協方差矩陣來刻畫其不確定性，適合在質量評估工作準備階段質量數據處理方面減少不確定性誤差對質量數據的影響。