基于遺傳BP神經網絡的耙吸挖泥船產量預測研究?

孫 健 李建禎 蘇 貞

（1.江蘇科技大學電子信息學院 鎮江 212003）（2.江蘇科技大學海洋裝備研究院 鎮江 212003）

1 引言

隨著世界化石燃料的逐漸減少和世界各地氣溫的上升，越來越多地關注節能減排和低碳化。然而，耙吸挖泥船對化石燃料的需求卻在不斷地增加，所以如何使挖泥船能耗低，效率高的工作已經成為挖掘行業研究方向的重點［1］。近年來，出現了大量關于耙吸挖泥船疏浚作業能耗分析和效率優化的研究。耙吸挖泥船干土方生產率是挖泥船性能的最重要指標，因此干土方的生產率預測是效率優化過程中的重要工作［2］。

耙吸挖泥船疏浚過程模式是一種復雜的非線性動力學模型，模型是受各種因素的影響，包括：船舶設備參數，土壤類型參數和施工控制參數［3］。J.Braaksma建立了耙吸挖泥船動態模型，并采用預測控制算法優化整體性能［4］。Rhee，C.van詳細分析了沉淀過程溢流損失模型［5］。王培生等闡述了主要的數學模型獨立開發，用于耙吸挖泥船，根據沙床的變化提高工作效率以優化其生產［6］。倪福生等研究了利用神經網絡預測絞吸挖泥船的性能［7］。耙吸挖泥船疏浚模型主要包括泥泵管線模型和泥艙沉積模型。在耙吸挖泥船泥泵—管線模型中，存在許多因素影響其準確性，而且各個因素之間的相互影響并不能夠準確地知道［8］。在進行溢流裝艙時，泥沙通過耙頭、泥泵、管線進入泥艙，由于溢流筒高度低于泥艙液面使得部分泥沙流出泥艙。在進行干土方生產率預測時不可避免地需要對溢流損失進行計算，但是溢流密度和溢流流量不能通過傳感器得到可靠的測量，并且歷來沒有很好的模型計算方法。因此急需一種可以解決以上問題的模型算法。

近年來，神經網絡算法和進化算法的結合受到了人們的廣泛關注，形成了一個稱為進化神經網絡的領域（Yao 1999）。由于這一領域的研究非常活躍，得到了許多有價值的結論和結果，其中一些已經成功應用。鑒于以上原因，通過應用遺傳BP神經網絡直接構建輸入為控制參數，輸出為干土方生產率的預測模型是極佳的選擇。輸入的控制參數包括：船舶的速度、耙頭對地角度、波浪補償壓力、泵速、船舶吃水、溢流桶高度。

2 遺傳算法優化BP神經網絡研究

反向傳播（BP）神經網絡在自學習，自適應和泛化能力上表現出良好的性能，但是卻具有容易陷入局部最小，收斂速度差的缺點［9］。為了克服BP神經網絡的不足，在神經網絡的研究和設計中引入了許多優化算法，如構建基于粒子群優化算法的神經網絡（Chen和Yu 2005），并使用進化算法優化神經網絡（Eysa and Saeed 2005；Harpham 2004；Ven?katesan 2009；Yao and Islam 2008），這被證明是可行和有效的。遺傳算法（GA）是啟發式隨機搜索算法，也是進化算法之一。比之其他優化算法，GA的全局搜索能力具有一定優越性，可以在沒有誤差函數的梯度信息的情況下學習近最優解，是優化，搜索和機器學習的強大工具（Yao 2004）。

2.1 BP神經網絡算法

BP網絡基本上是一個漸進式算法，旨在最小化權重空間中的誤差函數。在訓練神經網絡時，調整權重以減少總誤差。通過證明，針對一些復雜的非線性函數，原則上已經證明，具有一個隱藏層的BP網絡模型也是可以滿足需求的。因此，我們的研究中采用了三層BP模型。在應用過程中，輸入層的神經元個數和輸出層神經元個數根據實際需求確定。假設BP神經網絡的輸入神經元個數為m、隱藏層神經元個數為p，輸出神經元個數為1，則其隱藏層各節點的輸入為

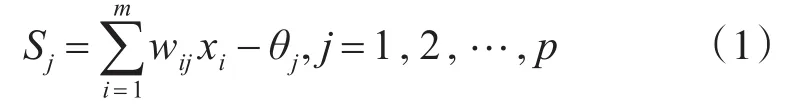
式中，wij為輸入層至隱藏層的連接權值；θj為隱藏層節點的閾值。

BP神經網絡轉移函數采用Sigmoid函數f(x)=1/(1+e-x)，則隱藏層節點的輸出為

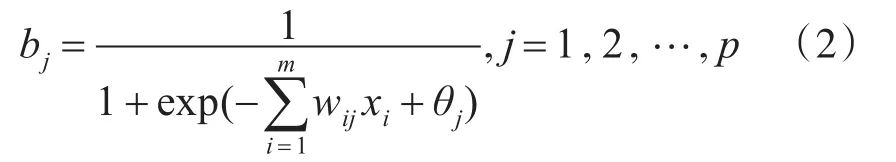
輸出層節點的輸入、輸出分別為

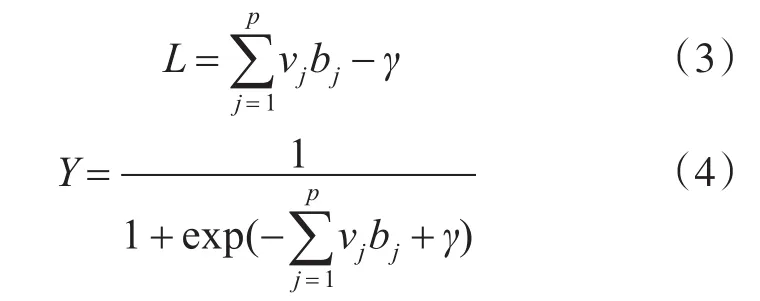
式中，vj為隱藏層的連接權值；γ為輸出層的閾值。

2.2 遺傳算法

1）遺傳算法原理

遺傳算法是進化算法之一，它包含著由一群染色體構成的種群，其中染色體是我們想要解決的問題的候選解決方案。染色體通常被稱為遺傳算法語境中的字符串。一個字符串反過來講是由許多基因組成，而這些基因可能帶有一些數值，稱為等位基因。與每個字符串相關聯的是適應度值，它決定了一個字符串的“好”。適應度值由適應度函數確定，可以將其視為我們想要最大化的一些利潤或最小化的誤差。

2）遺傳算法實現步驟

種群初始化：遺傳算法對優化的問題進行編碼，在編碼中，可以采用實數進行編碼，也可以采用二進制編碼，并對交叉規模、交叉概率、突變概率、初始種群數、遺傳代數進行初始化。

適應度函數：計算出個體的適應度值，根據適應度值判斷個體優劣，我們采用實際值與預測值之間的差值作為適應度，適應度越小則該個體的適應能力越強。

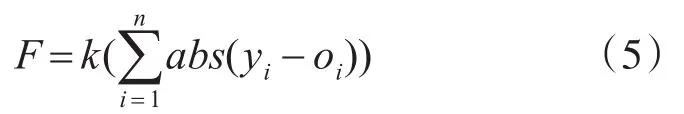
式中，n為網絡輸出個數；yi期望輸出；oi預測輸出；k為系數。

選擇：這是一個將染色體復制到下一代的過程。具有較高適應度值的染色體有更多的機會進入下一代。可以使用不同的方案來確定哪些染色體存活到下一代。經常使用的方法是輪盤賭輪選擇，其中輪盤賭輪分成多個時隙，每個染色體一個。插槽的大小根據字符串的適應度而定。因此，當我們旋轉車輪時，最好的染色體是最有可能被選中的。染色體被選擇的概率 pi為

式中，fi為染色體適應度；N為種群大小；k為系數。

交叉：一個染色體的一部分與另一個染色體的一部分組合。這樣，我們希望將一個染色體的良好部分與另一個染色體的良好部分相結合，在操作后產生更好的染色體。這個操作需要兩個染色體，即父母，并生成兩個新的，即后代。ak和al交叉方法為

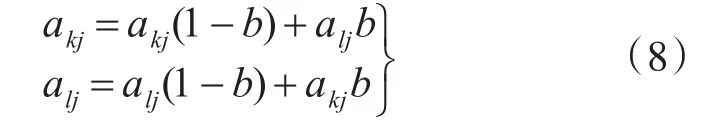
式中，b為［0，1］內的任意數。

變異：染色體中隨機選擇的基因將獲得一個新值。目標是在種群中引入新的遺傳物質，或至少防止其遺失。在突變下，一個基因可以獲得一個在種群之前沒有發生過的或由于繁殖而丟失的值，變異方法為

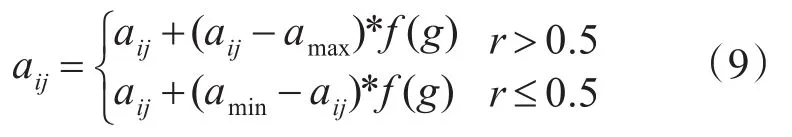
式中，amax為 aij的上限；amin為 aij的下限；為隨機數；g為進化次數；Gmax為最大迭代次數；r是在［0，1］內的任意數。

2.3 遺傳算法優化BP神經網絡方法和步驟

遺傳算法優化神經網絡的可分為三個階段。第一階段是決定連接權重和閾值的表示，即我們是使用二進制字符串形式還是直接使用實數形式來表示連接權重和閾值。由于本文使用實數編碼遺傳算法，我們要做的只是將每個神經元的連接權重和閾值設置為其對應的基因片段。然而，使用二進制編碼的簡單遺傳算法（SGA）來解決具有太多設計變量的優化問題難以達到收斂［10］。因此，使用實數編碼遺傳算法來克服SGA的缺點。第二階段是通過構建相應的神經網絡來評估這些連接權重、閾值的適應性。目標函數（如式（5）所示）被直接選擇為適應度函數。由于ANN的泛化，其模型可以作為優化算法的知識源。該方法可以實時計算目標函數。第三階段是根據遺傳算法的適應度，應用遺傳算法進行選擇、交叉和變異操作等進化過程。當適應度小于預定義值時，進化就停止了。

優化神經網絡學習過程包括兩個階段：首先使用GA搜索網絡的最優或近似最優連接權重和閾值，然后使用BP神經網絡調整最終權重。使用GA-BP算法來實現網絡權重和閾值的學習最優值的步驟，如圖1所示。首先，種群初始化完成，然后通過測量總均方誤差的值來評估每個染色體的適應度，參見方程式（2）～（5）。在評估所有染色體后，通過使用繁殖（選擇）算子從當前群體中提取染色體來創建中間種群。在本研究中，基于排序算法的輪盤選擇被應用于選擇算子。根據輪盤運算符排列后的相對適合度，選擇染色體，并將其置入中間種群。最后，通過將交叉和突變算子應用于中間群體的染色體來形成下一代群體。然后評估通過選擇，交叉和突變算子新建的新染色體，并重復所有染色體的評估和創建程序，直到滿足停止標準。GA的基礎是隨著個體從一代傳遞到下一代，通過遺傳算子不斷改進種群的適應度。以這種方式，ANN權重和閾值被初始化為最佳種群成員的染色體。該過程通過對GA建立的初始連接權重和閾值應用BP算法來完成。如果BP停止條件為假，則更新權重和閾值；否則，它們被保存并提供用于將來的干土方生產率預測。

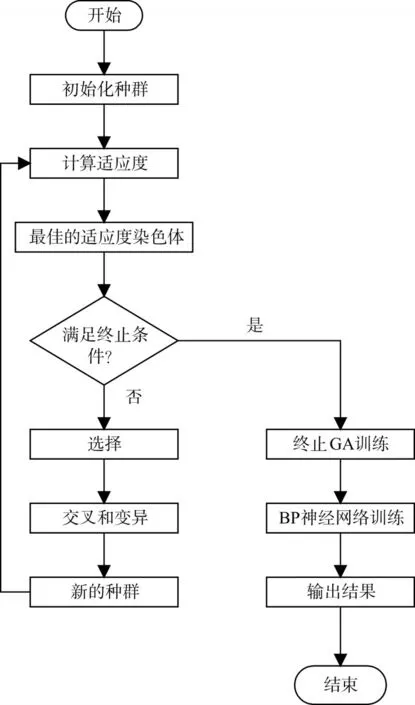
圖1 遺傳算法優化BP神經網絡流程圖

3 預測模型建立及驗證

3.1 模型建立

耙吸挖泥船干土方生產率預測網絡如圖3所示，影響模型的參數有很多，選取船舶的速度、耙頭對地角度、波浪補償壓力、泵速、船舶吃水、溢流桶高度作為模型的輸入。耙吸挖泥船的泥泵吸入泥沙密度會隨著航速的增加而減少，從而導致疏浚效率降低、能耗增大［11］。在一定范圍內，耙頭對地角度越大泥沙吸入量就越大。對于不同的土質對高壓沖水泵的需求不同，使用高壓沖水泵能夠提高耙頭的破土能力和泥沙在混合物中的濃度。溢流筒高度的有效調節使得溢流損失減少，提高疏浚效率，減少疏浚時間。耙頭的對地壓力可以通過波浪補償器壓力來進行調整，合適的對地壓力可以減少對耙頭的損傷，并且對有效疏浚起到很重要的作用［12］。實驗為了突顯預測模型的性能，分別建立了兩個預測模型：BP神經網絡預測模型、遺傳算法優化BP神經網絡預測模型。對同一周期疏浚數據進行預測，并進行對比實驗。實驗的誤差評價體系采用平均絕對誤差MAE，平均相對誤差 perror，即

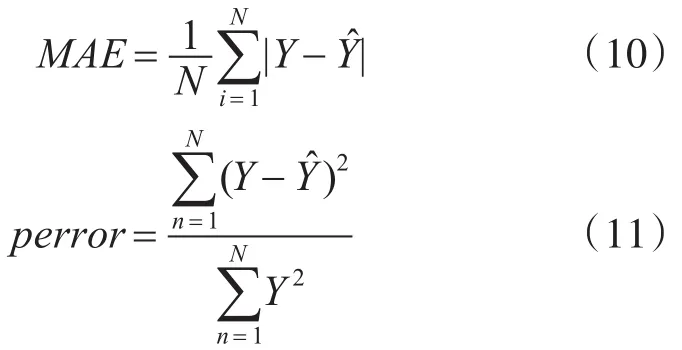
1）遺傳算法參數選擇：遺傳算法種群數目和遺傳代數太小則很難找到最優解，過大則增加了算法尋優的時間，因此論文中種群大小為10，遺傳代數為20；交叉概率和變異率過大則會破壞優化的個體，過小又很難產生新的個體，文中交叉概率設為0.4，變異率設為0.1。

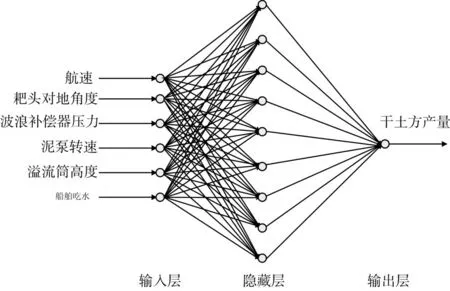
圖2 BP神經網絡模型拓撲

2）BP神經網絡參數選擇：輸入層有6個節點，輸出層有1個節點，隱含層節點數為9個，輸入層和隱含層之間有6*9=54個權值，隱含層和輸出層之間有1*9=9個權值，隱含層有9個閾值，輸出層閾值為1個，所以遺傳算法優化參數為54+9+9+1=73個。神經網絡迭代次數設為200，學習效率為0.24，目標誤差為0.0001。

3.2 耙吸挖泥船干土方生產率預測的驗證

數據來自于2016年4月廈門港興建的“新海虎8”號耙吸挖泥船收集。“新海虎8”號是一艘10000立方米的自航耙吸挖泥船，滿載吃水8m，最大挖深達35m。數據包含船舶的速度、耙頭對地角度、波浪補償壓力、泵速、船舶吃水、溢流桶高度、干土方生產率。我們收集了有5船周期數據。前4船數據用于訓練網絡，最后一船數據用于預測。為了評估遺傳算法神經網絡的性能，本文將BP神經網絡與遺傳BP神經網絡預測結果進行對比。圖3為BP神經網絡預測干土方生產率結果、遺傳BP神經網絡預測干土方生產率結果和希望值。圖4為兩種預測方法產生的干土方生產率相對誤差。

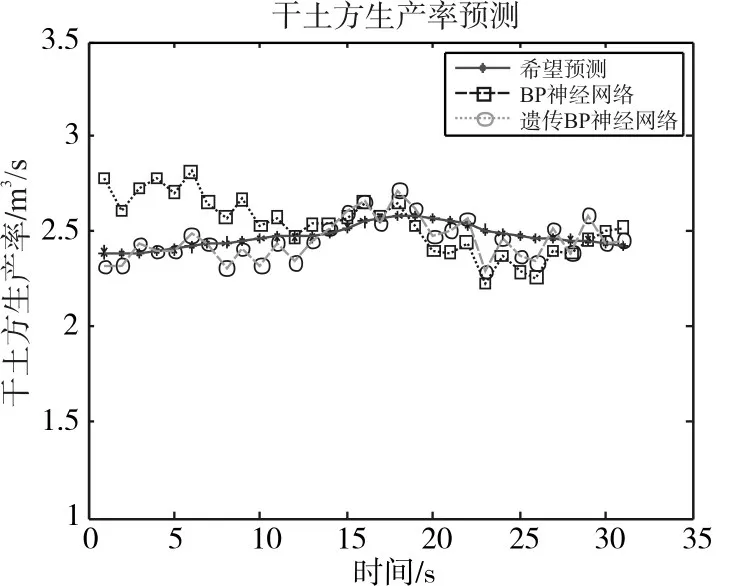
圖3 干土方生產率預測結果比較

圖4 干土方生產率預測相對誤差

從圖3可以看出兩種預測模型都能夠很好地反映干土方生產率的變化趨勢和規律，說明兩種預測模型都能較好預測干土方生產率。結合圖4和表1可以得出，經過遺傳算法優化后的BP神經網絡預測結果更加精確。

表1 干土方生產率預測誤差

4 結語

在文中，遺傳算法優化的神經網絡的優點和關鍵問題已經被提出來，對耙吸挖泥船干土方生產率和控制參數關系進行建模。我們的方法采用實數編碼的GA策略，與反向傳播算法混合。遺傳算子被精心設計，以優化神經網絡，避免問題過早收斂和置換。實驗表明，該模型的預測性能優于傳統BP神經網絡，具有全局優化能力，并且擁有了更好的非線性擬合能力，使得預測結果的準確性更高。該算法可根據當前施工條件和給定的參數對耙吸挖泥船干土方生產率進行預測，提高疏浚產能。同時，有助于開發耙吸挖泥船的智能疏浚系統。考慮神經網絡和遺傳算法組合干土方生產率預測的一個問題是確定最優神經網絡拓撲，本實驗中描述的神經網絡拓撲結構是手動確定的。一種替代方法是將遺傳算法應用于神經網絡結構優化，這將是我們未來工作的一部分。