基于BELLHOP模型的水下信道仿真方法研究?

李 孟 周榮艷，2

（1.南陽理工學院 南陽 473000）（2.西北工業大學航海學院 西安 710072）

1 引言

隨著水聲信道建模技術的發展，衍生出很多建模技術，例如，拋物線方程法、波數積分算法等都是基于聲傳播的射線理論［1～2］。聲場射線理論因其計算簡潔，尤為適合求解和距離相關的聲場環境的特點受到科研人員的追捧［3］。射線模型以聲場中的聲源和接收點為出發點，兩點間的連線即為本征聲線［4～5］。計算接收點上的聲場就因此被簡化了很多，只需知聲源和環境文件即可通過兩點之間形成的本征聲線進行計算，這使得仿真的過程變得更加簡單，并且只需要一個很小的基陣進行采樣便可以達到觀察大規模海洋聲學特征的目的［6］。

基于聲場射線模型的諸多特點，結合實際科研需要，本文采取基于BELLHOP射線模型的方法對水聲信道進行仿真研究。本文在Matlab開發仿真平臺上，對海洋水聲環境中的聲速剖面、幾何結構、海底地形及聲波在海洋界面中的反射和折射損失等各種相關參數進行輸入和設置［7］，通過基于Bell?hop模型程序的處理，得出海洋水聲環境中水聲聲波的幅度、入射角和通信時延等信息。提取與傳感器節點接收信號相關的傳遞函數參與運算，同時對聲線數目的多少與傳感器節點的最優節點放置之間的關系進行研究。

2 水下聲場建模

2.1 BELLOP模型概述

BELLHOP模型是依據射線跟蹤從而在海洋環境之中預測聲壓的模型，是由 Porter和 Bueker［3］在1987年編寫的。這種射線跟蹤結構使得其算法十分的簡單，它是基于幾何和物理的傳播規律，可以實現包括高斯波束和帽形波束等多種類型的射線。BELLHOP能產生各種有用的輸出信息，包括傳輸損耗，本征聲線，到達和接收的時間序列等。BELLHOP模型在600Hz-30kHz的頻率范圍內的實驗數據與理論模型比較相符，所以被指定為美國海軍海洋預報10-100kHz頻帶聲傳播的標準模型［7］。使用BELLHOP模型對水聲信道仿真能夠有效地預測信道的數據以及工作性能。

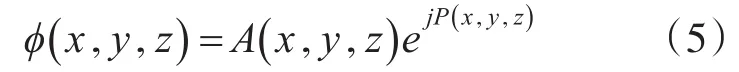
式（5）中P為程函，將這個解代入到Helmholtz方程中，并將實部與虛部分開，即可得到下面兩個關系式：的乘積，即為

方程（5）為實部，確定聲線的幾何形狀。方程（6）為虛部，確定聲波的振幅，這種函數分離是在假設幾何聲學近似條件成立的情況下才成立。射線理論模型不僅考慮了本征聲線，還考慮了折射-海面反射（RSR）、折射-海底反射（RBR）以及折射-海面反射-海底反射（RSRBR），為了考慮邊界作用以及體積效應通常將海洋環境參數等物理模型并入到射線模型中［8］。

2.2 傳遞函數h(t)

在Bellhop模型中可對海洋水聲環境中的聲速剖面、幾何結構、海底地形及聲波在海洋界面中的反射和折射損失等各種相關參數進行輸入及設置，得出海洋水聲環境中聲波傳播的幅度和時延，由此得到從目標聲源發射的信號到達傳感器節點處的傳遞函數h()

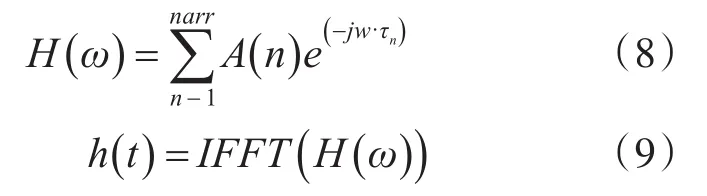
其中，narr表示到達的聲線個數。

將傳遞函數h(t)與目標聲源的發射信號做卷積，即可得到各個節點處的接收信號。若是對在Bellhop模型中提取的所有聲線到達時延信息與幅度信息進行研究非常復雜且不現實［9］，本文只考慮目標聲源對應于傳感器節點的所有路接收信號中的最大幅值，代表到達此傳感器節點處的接收信號，對應于傳遞函數的最大值hmax。同時對于TOA之類的定位算法［10～11］，只考慮節點處接收信號的最大幅度，也具有一定的現實意義。因此，本文中之后所用到傳遞函數h(t)均為hmax。

由上可知得到傳遞函數后，用傳遞函數與聲源發射信號做卷積，可得到陣列輸出信號，對陣列輸出信號進行波束形成處理，得到波束形成圖，通過波束形成的結果分析判斷信號是否存在。在上述水聲信道參數和傳播參數條件下，得到的傳遞函數如圖1所示。

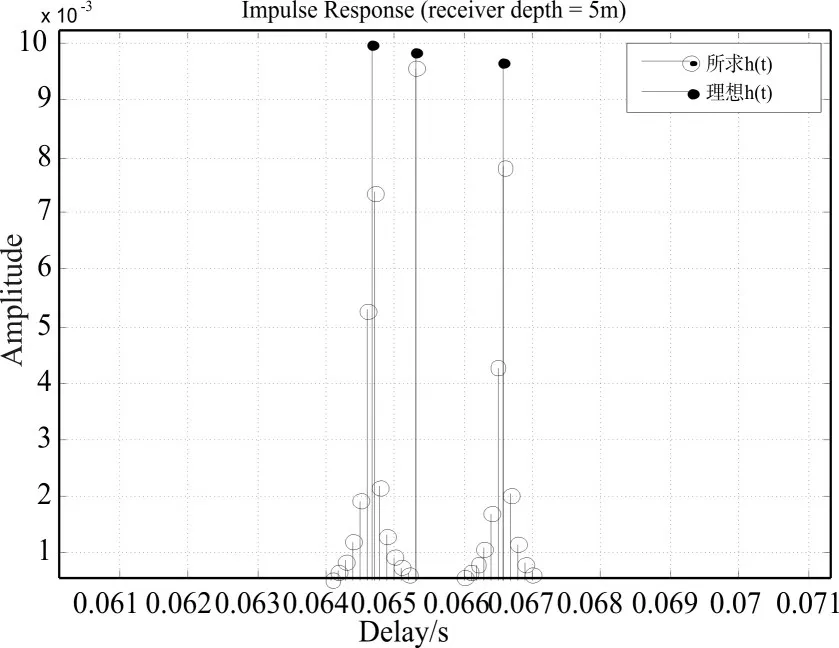
圖1 傳遞函數圖

3 實驗仿真

3.1 仿真參數設置

本節主要對基于BELLHOP的海洋聲場進行仿真和分析。目標聲源的信號參數如下：fc=1000Hz，Ts=0.005s，B=700Hz，信號1m處的信噪比SNR=70；

海洋環境參數和信號傳播參數如下表1、2所示。

根據上述參數設置，由Bellhop模型仿真得到水下聲線Munk圖，如下圖2所示。

由水下聲線Munk圖可知，聲線的疏密表征聲能的強度，聲線會聚的地方聲強大，聲線發散的地方聲強小［12］，當聲源在500m深度時，畫出的傳遞函數h(t)等高線圖與水下Munk圖對比可發現，傳遞函數h(t)變化與水下聲強的變化一致，即可用h(t)值來近似代表節點處于不同位置時接收信號的強弱。

表1 海洋環境參數表

表2 信號傳播參數

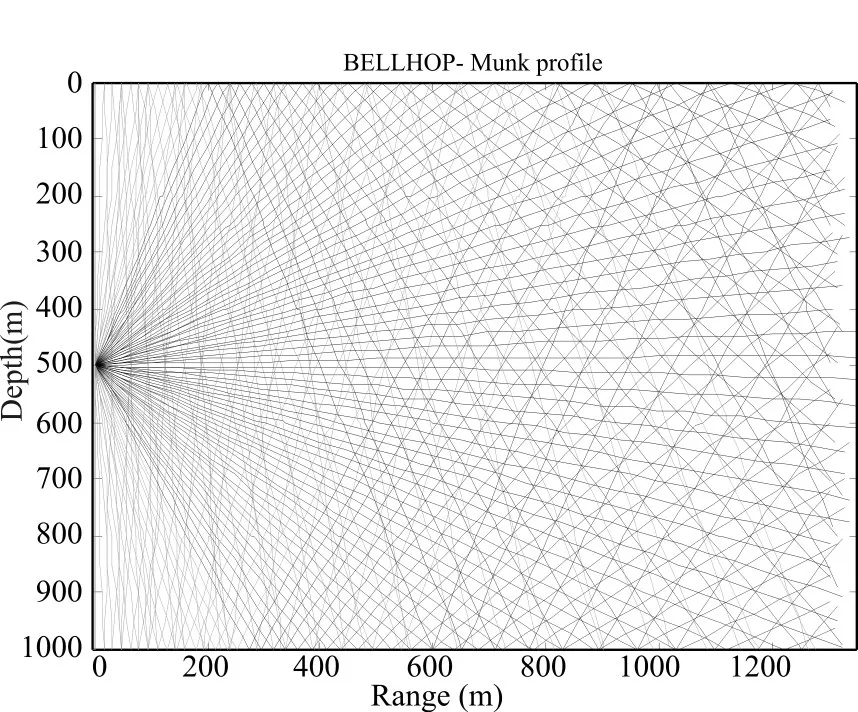
圖2 Bellhop模型仿真得到水下聲線Munk圖

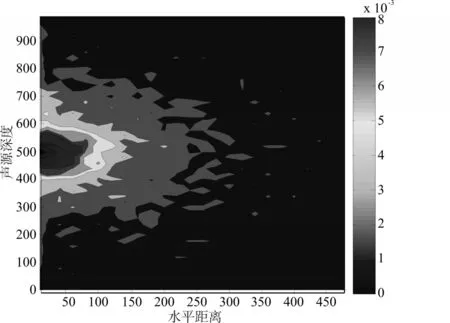
圖3 聲源深度為500m時傳遞函數h(t)等高線圖

設聲源深度范圍為0～1000m，傳感器節點的深度范圍為0～1000m，聲源與傳感器之間的水平距離范圍為0～1200m，設置間隔為10m，即以10m為間隔將聲源深度、傳感器節點深度和水平距離劃分為101*101*121的矩陣，分別求出矩陣中的h(t)值，這樣能夠保證聲源與傳感器節點在不同深度和水平距離處，都可以通過臨近的h(t)計算得到傳感器節點的接收信號。

3.2 水下傳感器節點的最優布局與聲線數目的關系

在本文中主要考慮單個目標聲源在Bellhop模型下的最優布局時與聲線數目的關系，假定聲源在［500，500］坐標處，選取5個節點采用遺傳算法［］來進行布局。為了證明聲線設置的多少對布局結果的影響，分別在Bellhop的*.env文件中設置聲線個數為31條和161條來進行仿真。

聲線數為31時優化布局結果如圖4（a）所示。之后，將節點放置于聲線圖中，由于此時的聲源為全向型點源，所以在*.env文件中設置發射角度為-180°～180°，此時聲源位于500m的深度，在聲線圖中點源的位置坐標為［0 500］，將節點的X軸坐標-500，Y軸坐標不變，將其表示在聲線圖中，如圖4（b）所示。由圖4（b）可知，最優布局時的五個節點坐標都位于聲線上。

聲線數為31時優化布局和與聲線的關系如圖4中（a）和（b）所示。

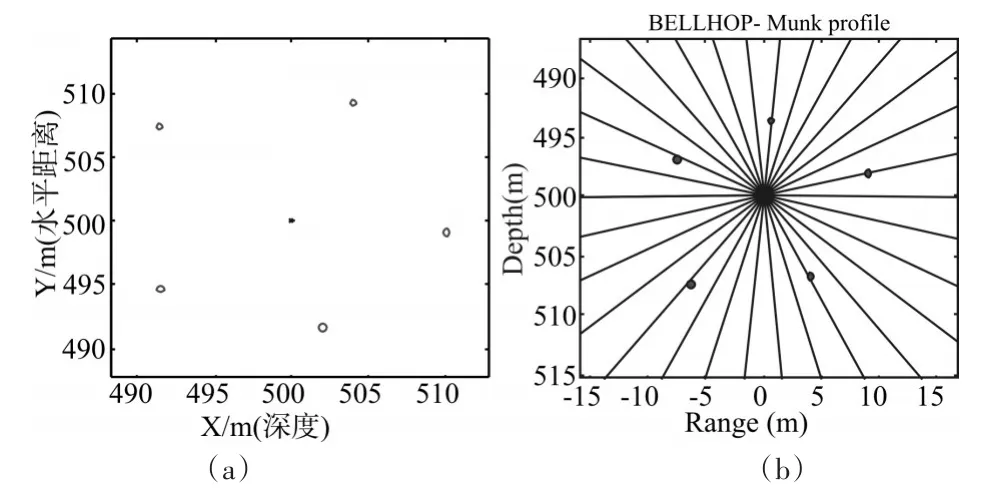
圖4 聲線條數為31時候的5個節點布局圖和節點與聲線關系圖

設置同樣的數據和條件，只是將聲線數目變為161，節點布局圖與聲線圖如圖5中（a）和（b）所示。

由圖4和圖5可知，無論聲線數目多少，優化布局的節點位置始終置于聲線上。除此之外，針對于單個目標聲源，選取5個節點采用自適應遺傳算法對其進行最優布局，可從圖中看出五個節點都布放于聲源周圍較近的位置，這一布局也符合文獻［10］的結論。

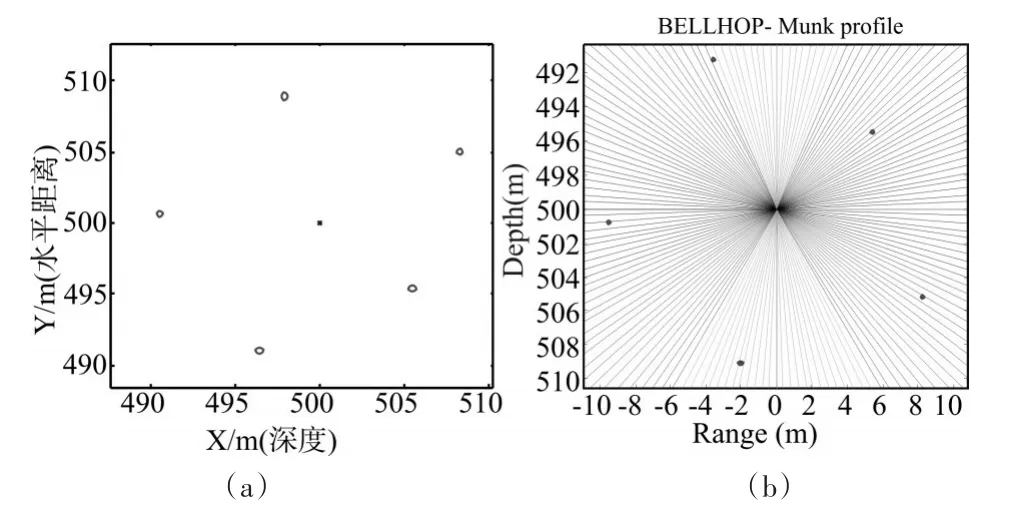
圖5 聲線條數為31時候的5個節點布局圖和節點與聲線關系圖

4 結語

本文主要基于BELLHOP模型對水下信道進行仿真，并研究分析目標聲源探測的方法和陣列最佳布放方法與聲線的關系。首先對水下聲場建模基本原理進行介紹，利用BELLHOP模型對水下信道進行仿真并得到所需要相關輸出參數，之后求得水聲信道中聲源到各個陣元的傳遞函數，通過改變聲源位置參數，得到各組相應的傳遞函數。最后研究采用遺傳算法的最優布局中節點的放置位置與聲線之間的關系。仿真實驗結果表明，采用傳遞函數能夠很好地對水聲信道中信號的傳播途徑模擬，此外，無論聲線數目的多少，最優節點始終放置在聲線上。