管道機器人跨井機構的設計與研究

，，，，

(南京理工大學機械工程學院，江蘇 南京 210094)

0 引言

管道在腐蝕、重壓等作用下會出現裂紋、漏孔等一系列現象[1]。同時，隨著管道使用時間的增加，管道內壁會發生不同程度的結垢和雜質粘附，造成管道運輸效率降低[2]。所以在使用過程中，管道需要定期進行檢測、維修、清理，保證管道運輸安全和效率[3]。但是，空間狹窄或內部環境惡劣的管道限制工作人員進入管道內部[4]。因此，管道機器人作為一種爬行設備逐步發展起來。管道機器人的發展為管道檢測、維護提供了新的技術手段，極大提高了管道維護效率。

近年來，我國機器人技術取得了快速發展。典型的有螺旋式管道機器人、蠕動式管道機器人、伸縮式管道機器人、壓差式管道機器人[5-8]。目前的管道機器人大多能順利通過水平管道和一定傾斜程度的上升管道。但是在實際下水管道中，管道內部存在沉井，阻礙管道機器人在管道內連續行駛。當前還沒有關于具有跨越沉井功能機器人的研究。針對上述問題，設計出一種能跨越沉井的管道機器人。

1 機器人跨越沉井的過程

管道機器人主要用于直徑700 mm的管道，沉井兩側的管道在高度方向存在誤差，機器人工作管道具體參數是：管道直徑為700 mm；沉井直徑為900 mm；高度誤差為50 mm。

管道機器人采用分段式設計，分為車頭、車身、車尾3個部分。機器人跨越沉井的過程相應的也分為3個階段，車頭、車身、車尾分別在3個階段中依次通過沉井，圖1是管道機器人通過沉井示意圖。

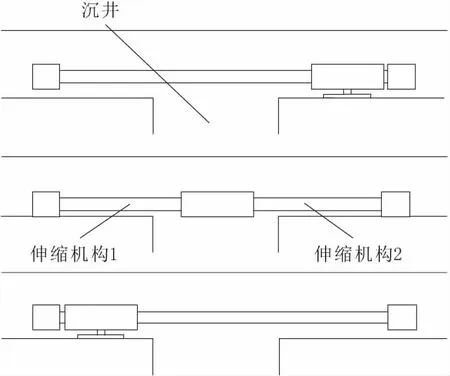
圖1 管道機器人通過沉井

第1階段，啟動蝸輪蝸桿升降裝置將機器人抬起一定高度。機器人上升到預定位置后，此時機器人車輪均處于懸空狀態。機器人車身內部有兩個相同的伸縮機構，分別和車頭車尾連接。啟動伸縮機構1，將機器人車頭送至沉井對面。第2階段，控制蝸輪蝸桿升降裝置，讓支撐裝置恢復至初始位置，機器人車輪重新接觸管道。在關閉伸縮機構1的同時開啟伸縮機構2，通過交互利用兩個伸縮機構，讓機器人車身到達沉井對面。第3階段，車身到達沉井對面后再次啟動蝸輪蝸桿升降裝置，讓支撐裝置將機器人重新上升到預定位置，機器人車輪再次懸空，關閉伸縮機構2，伸縮機構2回縮讓車尾到達沉井對面。最后關閉蝸輪蝸桿升降裝置，讓支撐裝置恢復至初始位置，管道機器人順利通過沉井。通過3個階段，機器人按照車頭、車身、車尾的順序依次通過沉井。

2 機器人升降機構的設計

圖2是管道機器人升降機構機械結構圖。上方是蝸輪蝸桿升降裝置，電機驅動蝸桿，蝸桿帶動蝸輪轉動，蝸輪轉動會讓絲杠轉動，實現上下移動目的。下方是支撐裝置，跨越沉井時起到支撐作用。

蝸輪蝸桿升降裝置的絲杠和支撐裝置的連接桿間通過軸承連接，圖3是絲杠和支撐裝置連接示意圖。通過軸承和方形連接桿限制作用，使支撐裝置只能在預定軌道內上升和下降，避免支撐裝置隨絲杠轉動與管道內壁發生接觸。當支撐裝置升降至預定位移后，因為蝸輪蝸桿的自鎖功能可以使管道機器人停留在預定位置。

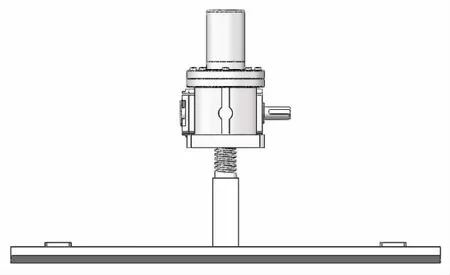
圖2 升降機構機械結構

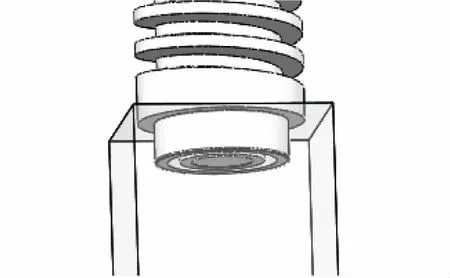
圖3 絲杠和支撐裝置連接

3 機器人跨越沉井的力學分析與仿真

3.1 機器人跨越沉井的應力分析

管道機器人在跨越沉井的3個階段中，第1階段和第3階段都需要利用支撐裝置，通過支撐裝置，讓車頭和車尾能順利通過沉井。為最大程度貼合管道內壁，支撐裝置底面采用曲面板。2個階段受力情況類似，以第1階段為例，圖4是第一階段中支撐裝置支撐面受力示意圖。

圖4 支撐面受力

車頭質量為m1，車身質量為m2，車尾質量為m3，重力加速度為g，單位長度的伸縮機構質量為m，伸縮機構的速度為v，工作時間為t，支撐底板厚度為a。根據力的平移定理，車頭和伸縮機構分別都對支撐底面施加水平向下的力和逆時針方向的力偶。將兩個力合并得到支撐裝置承載區受到的合力G=m1g+m2g+m3g。車頭產生的力偶M1=m1gvt，伸縮機構因伸長產生的力偶M2=0.5mgvt，2個力偶合成的總力偶M=m1gvt+0.5mgvt。總力偶M會對支撐裝置連接桿造成傾覆作用，在力的作用效果上，可以通過水平向左的軸向力來代替。支撐底板受到豎直向下的合力G，因此，軸向應力σc為和正壓力σp分別為：

(1)

圓柱曲板的軸壓屈曲應力和圓柱曲板的外壓屈曲應力分別為：

(2)

式中kc為圓柱曲板受軸壓作用下的屈曲系數；ky為圓柱殼體受外壓作用下的屈曲系數；E為彈性模量，單位是MPa；γc為彈性泊松比；a為曲板厚度，單位是mm；b為曲板較短邊邊長，即曲板的寬度,單位是mm；c為圓筒長度，單位是mm。

因此，圓柱曲板的軸向應力σc和圓柱曲板側壓應力σp必須滿足σc<σcrc，σp<σcrp。

根據力的合成定理，軸向應力與正壓力的合應力σ及合應力與水平方向夾角θ分別為：

(3)

從合應力σ可以得到：隨著時間t增加，應力σ會隨時間t增大，當車頭達到沉井對面，即伸縮機構伸長到最大時，應力σ達到最大值，同時應力與水平方向夾角θ達到最小值。

3.2 機器人跨越沉井的應變分析

管道機器人跨越沉井時需要升高機器人，讓機器人車輪和底盤離開管道。因為沉井兩側管道高度存在誤差，尤其是沉井對面管道比機器人所在管道高時，必須通過控制升降機構伸長的長度保證機器人不與管道發生接觸。機器人跨越沉井過程中，支撐裝置連接桿因機器人重力影響會產生彈性變形，在跨越過程中機器人會和理想情況發生一定程度偏移，因此升降機構上升高度需要考慮支撐桿彈性變形的影響。在機器人跨越沉井第一階段，因為支撐裝置的支撐面與管道內壁緊密貼合，所以可以將連接桿底部視為與管道固連，支撐裝置連接桿在第一階段的受力如圖5所示。

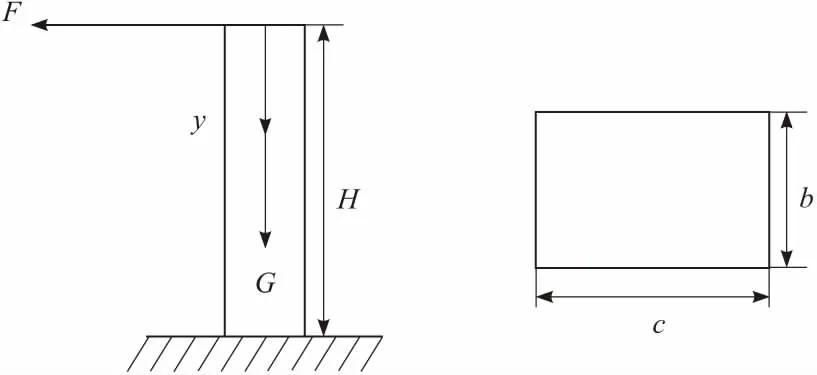
圖5 連接桿受力

連接桿在豎直方向上的彈性變形量為：

(4)

E為彈性模量；b和c分別為連接桿橫截面的長和寬，與前文出現的含義相同；H為升降機構伸長的長度。

連接桿頂部受到水平向左的力，連接桿會發生彎曲變形，連接桿向左移動的位移為δ，可以得到：

(5)

E為彈性模量；I為矩形截面對中性軸的慣性矩。

對式(5)進行兩次積分，同時不考慮連接桿在豎直方向上的彈性形變，則當y=H時，連接桿的轉角和位移均為0，將邊界條件和慣性矩代入后可得連接桿的位移和轉角方程為：

(6)

從式(6)可以得到，當y=0時，位移和轉角最大，分別為：

(7)

正負號為位移和轉角方向，F用式(1)表示。

因為連接桿彈性變形的原因，會導致機器人向下傾斜，車頭底部在豎直方向上高度變化最大，圖6是機器人跨越沉井第一階段的位移變化圖,圖中l1為車頭長度，l2為伸縮機構伸長后的長度，l3為車身的長度。因為車頭高度h1必須大于沉井兩側在高度上的最大誤差c，根據工作管道參數可知c=50 mm，最終推導得出升降機構理論最小伸長長度為：

(8)

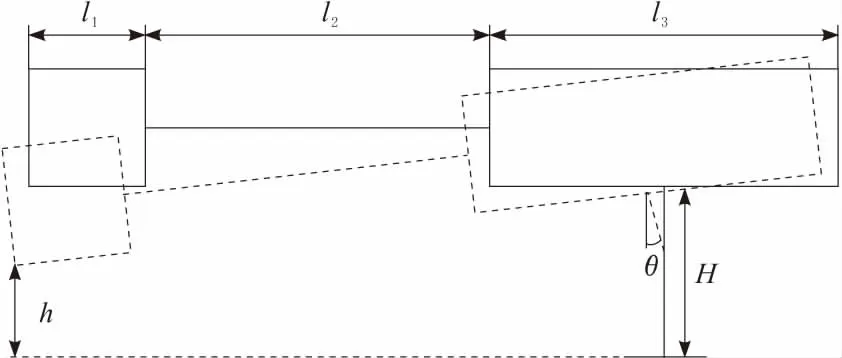
圖6 機器人位移變化

3.3 基于ANSYS的仿真分析

為驗證支撐裝置受力情況，在ANSYS Workbench中對支撐裝置進行應力應變分析。

根據管道機器人質量、電機轉速、絲杠導程，設置底面為固定面，施加300 N壓力和大小y=7.5×tN·m力偶，時間設置為30 s。圖7～圖10分別是10 s、20 s、30 s時支撐裝置的等效應力圖以及30 s時支撐裝置的等效應變圖。

圖7 10 s時支撐裝置等效應力

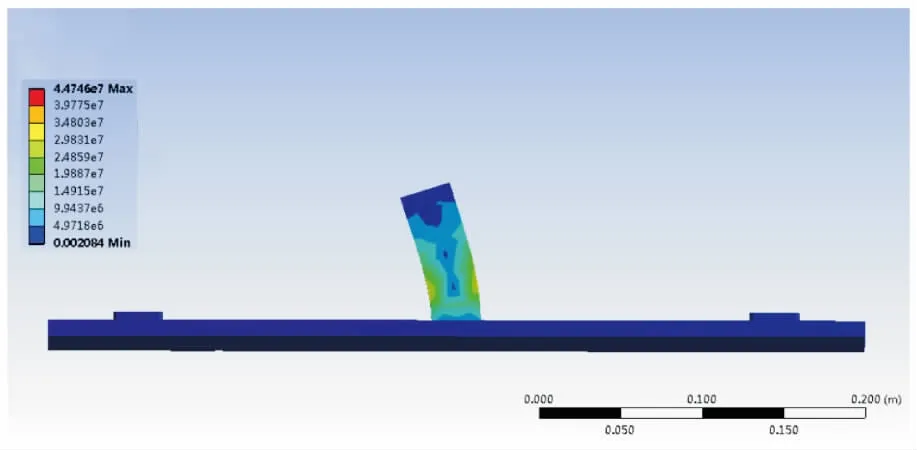
圖8 20 s時支撐裝置等效應力

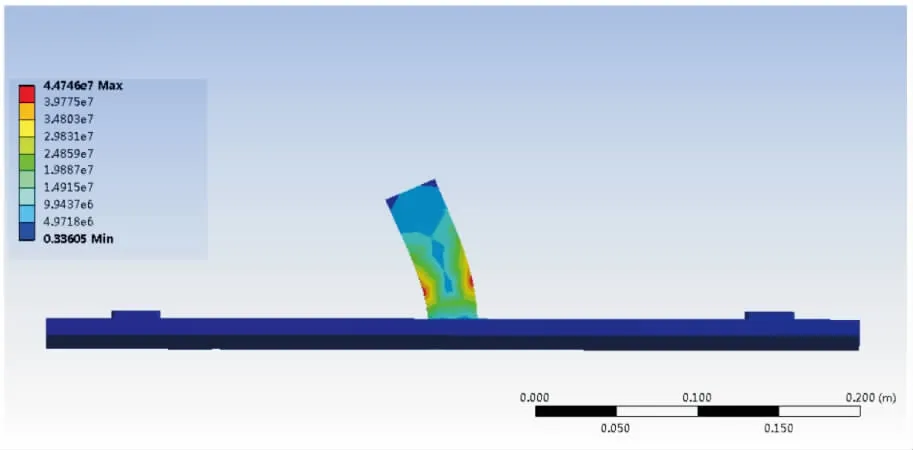
圖9 30 s時支撐裝置等效應力

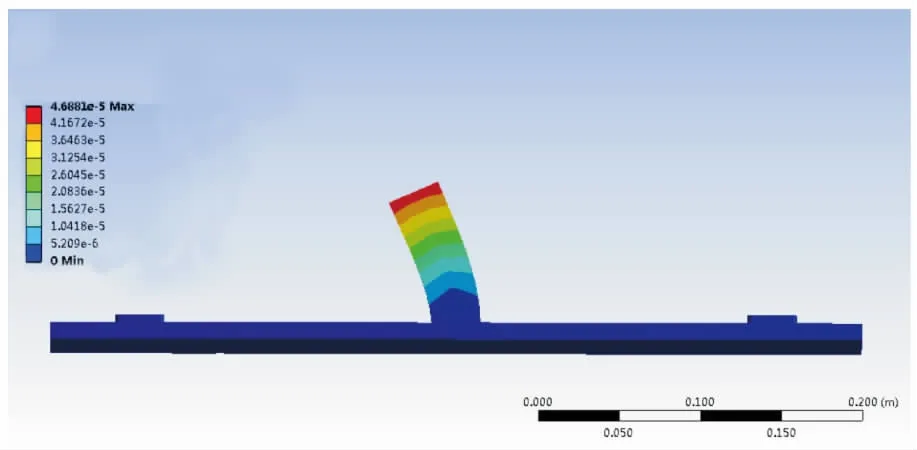
圖10 30 s時支撐裝置的等效應變

根據10 s、20 s、30 s時支撐裝置等效應力圖，能夠得出應力隨時間增大，并且30 s時有最大應力，最大應力為4.474 6×107Pa。同時在支撐裝置受力過程中，每個階段最大應力始終與水平方向呈現一定角度，且該夾角隨時間而逐漸減小。

圖10是30 s時支撐支撐裝置應變圖，最大應變發生在支撐桿最頂端，支撐裝置的最大變形量為4.688 1×10-5m。根據支撐裝置相關尺寸，求出理論最大位移δmax=3.472 2×10-5m。

理論值和仿真值接近。產生誤差的原因在于H的實際值不等于50 mm，其值要大于50 mm。同時因為連接桿在豎直方向上也存在彈性變形，會對連接桿位移和轉角造成影響，上述兩點原因造成了理論值偏小，兩者數據對比也進一步表明應力公式和升降機構理論最小伸長長度的合理性。

4 結束語

采用分段式設計方法，讓機器能夠按照車頭、車身、車尾的順序依次通過沉井。針對連接桿彈性變形問題，理論推導出連接桿應力方程和連接桿位移轉角方程，并求解出最大位移和轉角的表達式。根據最大位移和轉角，進一步求解出升降機構理論最小伸長長度。利用ANSYS Workbench對支撐裝置受力情況進行仿真，驗證了應力公式的正確性，同時將最大位移的理論計算值和仿真結果值進行對比，并得出產生誤差的原因，這為后續管道機器人樣機開發和優化奠定基礎。