帶電導體為橢球體的電場分布

張拴柱

（長治學院 電子信息與物理系，山西 長治 046011）

在一般的電磁學教科書中，討論帶電導體球的例題、習題很多，但對帶電橢球體的問題并沒有涉及到，原因是橢球體問題需要用到的數學知識復雜一些，因此一般的電磁學教科書避而不談。文章采用橢球坐標系，對橢球體外場的分布以及其他的一些問題展開討論。

1 帶電導體橢球體的場分布

設：在真空中有一帶電量為Q的導體橢球體，其橢球面方程為：

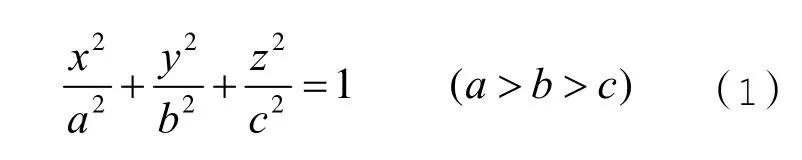
在橢球坐標系中，點M在空間的橢球坐標系，是這樣的三個有序數（ξ，η，ν），它與直角坐標系的關系是：

坐標 ξ，η，ν滿足

在橢球坐標系中，坐標曲面分別是：

ξ=常數：為橢球面

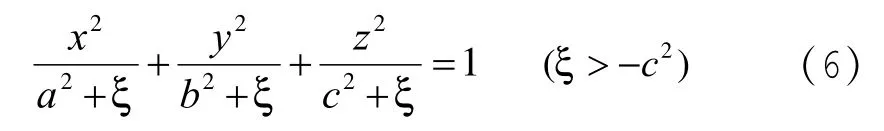
η=常數：為單葉雙曲面

ν=常數：為雙葉雙曲面

橢圓坐標系的拉梅系數

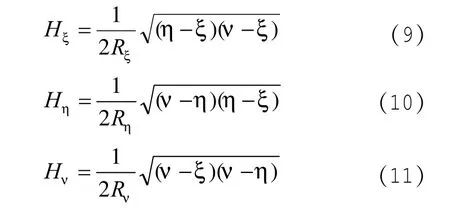
其中，

在橢球坐標系中，電勢φ的拉普拉斯方程[1]為

φ的邊界條件是：在（1）式的橢球面上φ為常數，而在遠離導體橢球非常遠處φ應該趨于點電荷或帶電球體、帶電球面的電勢。

在一族橢球面即方程（6）中，當ξ=0就是帶電橢球體的橢球面方程，在橢球面上電勢φc是與η、ν均無關的常量，因此，如果φ只是ξ的函數，就可以滿足上面所說的邊界條件。這時拉普拉斯方程（12）式變為：

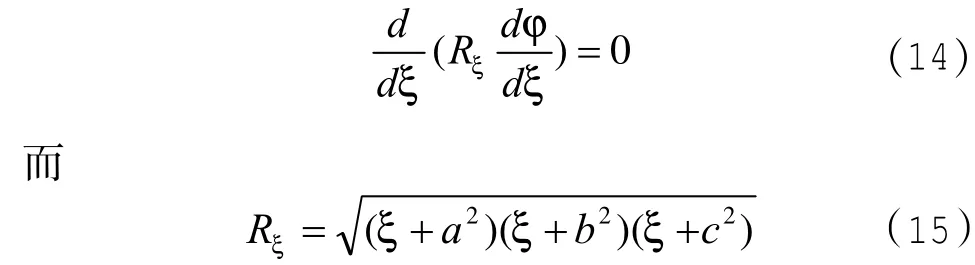
解方程（14）得：

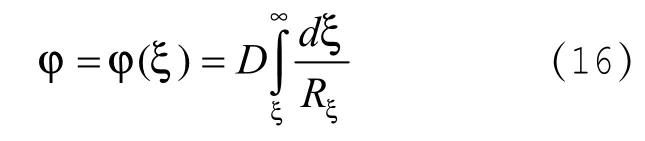
式中D是積分常數，由邊界條件確定。

再由E=-▽φ可求得電場強度為：

由（16）式可得：

電勢等勢面：

由于 φ=φ（ξ）只是一元函數，當 φ= 常數時，則一定有ξ=常數，而ξ=常數，則為一族橢球面組成

即上式為所求的電勢等勢面。

電力線：

由正交曲線坐標系知識可知，電力線應該滿足微分方程

由于 Eη=0，所以 dη=0，則 η=常數，而 η=常數，對應是一族單葉雙曲面

同理，由于 Eν=0，所以 dν=0，則 ν=常數，而 ν=常數，對應的是一族雙葉曲面

而式（22）和（23）組成聯立方程，即兩族曲面的相交線就是所求的空間電力線的分布函數。

下面把電勢、電場強度表達式由橢球面坐標系改寫為直角坐標系，并且確定積分常數D。

由正交曲線坐標系變換規則[3]可知，

由（2）式和（9）式可求得：

同理，根據（3、（4））和（10）、（11）式可求得：

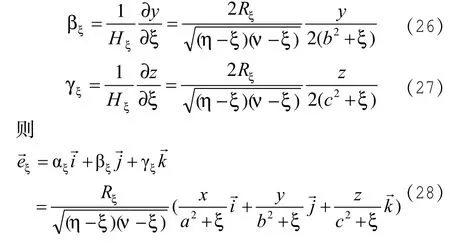
由（19）式得：

若場點在橢球面上時，取ξ=0，

把 η，ν換成 x，y，z表示出來

上式過渡的球面時，則取a=b=c=R

而半徑為R的帶電荷Q的球面公式

（33）式（34）比較可得：

（35）式代入（16）、（19）和（29）式，至此可寫出橢球體外電勢和電場強度公式

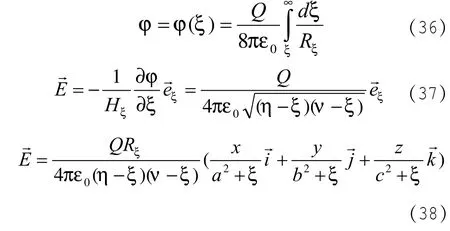
由（38）式進行一些討論：

當ξ=0時，即是帶電導體橢球面任一點的場

當ξ=ξ時，即ξ取任意一個值時，則它代表的是一族橢球面中的某一個橢球面，而在這個橢球面上任一點的場可以表達為：

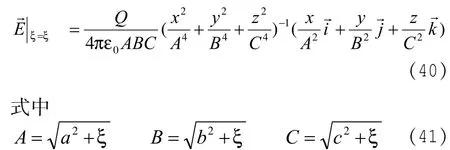
其實（40）式就是把（38）式中的η和ν用ξ表示出來了。而ξ的意義根據文獻[2]可知，與（1）式共焦的二次曲面

中，λ的三個互不相等的實根，三個實根大小次序選為ξ＞η＞ν，經過空間任一點的三個曲面（42），其中對應于λ=ξ的一個根是橢球，對應于λ=η的一個根是單葉雙曲面，對應于λ=ν的一個根是雙葉雙曲面[2]。

2 帶電導體橢球面上的電荷分布

由電磁場邊值關系

由（9）、（18）、（35）式得：

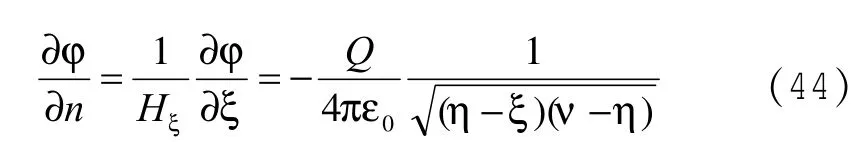
代入（43）式得：

（31）代入（45）式得：

幾個特殊點的情況：

（1）在x軸上兩個端點，即x=±a，y=z=0

（2）在y軸上兩個端點，即y=±b，x=z=0

（3）在z軸上兩個端點，即z=±c，x=y=0

由此看出，因為a＞b＞c，所以曲率大的地方，電荷密度越大，如x軸兩端點，反之，曲率小的地方，電荷密度越小，如z軸兩端點。

如果是球體時，x2+y2+z2=R2，a=b=c=R 則

3 兩個同焦點橢球面組成電容器的電容量

若有兩個同焦點帶電導體橢球面構成的電容器，方程為：

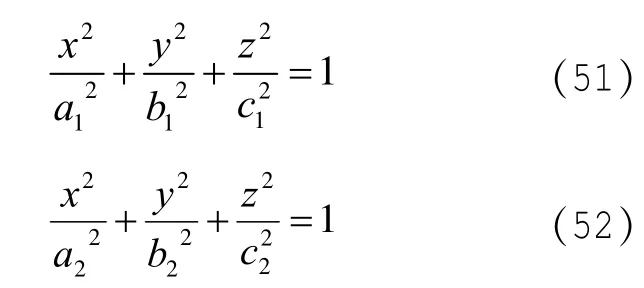
由（36）式可知，

第一個橢球面的電勢，注意：

第二個橢球面的電勢，注意：

所以橢球面構成電容器的電容量

特殊情況下，當a1=b1=c1=R1，a2=b2=c1=R2即兩個同心球面構成的電容器

回到一般教科書上的結果。