一種基于模糊控制的自適應互補濾波算法

陳國成，侯宗琰

（東北石油大學 電氣信息工程學院，大慶 163318）

四旋翼飛行器又稱為四軸飛行器（QUAD），其姿態解算是四軸飛行器能夠穩定飛行的基礎，也是近年來國內外高校和研究院所的研究熱點[1]。在現在的四軸飛行器上大都采用低成本捷聯慣性導航測量元件，其主要由陀螺儀、加速度計和磁力計組成。我們要獲得四軸的角度信息，就要對陀螺儀測得的角速度進行積分運算[2]。類似用在四軸飛行器上的這種低成本陀螺儀IMU器件易發散導致姿態漂移問題，需要進行慣性器件的慣導融合，其濾波融合才能獲得較為準確的三維姿態信息[3]。

鑒于此，有人提出采用卡爾曼濾波算法對數據進行濾波和融合以估計真實的姿態角[4]，并且還提出了基于四元數的擴展卡爾曼濾波器[5]以及梯度下降法[6]。然而，卡爾曼濾波器使用的觀測噪聲矩陣R和過程噪聲矩陣Q直接影響濾波效果，并且其準確值難以獲得[7]，擴展卡爾曼濾波也是近年來研究比較多的一種姿態解算的濾波算法[8]，但是該算法涉及到大量的矩陣運算，對飛控的處理器的性能要求較高[9]，梯度下降法計算量小，但是他的迭代步長是非動態的，其動態和靜態的估計性能難以兼顧，所以在實際應用中并不是最好的選擇。綜上所述，針對本文對于互補濾波姿態解算算法中互補參數固定的情況下很難實現在所有的狀態下都能得到最優的姿態估計，引入了模糊控制算法，把實時的姿態角和角速度作為模糊控制器的輸入進行互補參數實時的調整。

1 四旋翼飛行器坐標系的建立

我們想要解算出四軸飛行器的姿態，必須要建立導航坐標系和機體坐標系[10]。四軸飛行器一般采用“+”型或者“X”型，這里我們采用“X”型，使得飛行器更加靈活。

導航坐標系也稱為大地坐標系。起飛點是這個坐標系的原點。正北，正東和t天（北東天）構成該坐標系的X，Y，Z軸。本文標記為坐標系R。以四軸飛行器的中心為起點，機頭方向為Y軸，從上往下看，X軸由機身右側確定。這個坐標系通常被稱為體坐標系。本文標記為坐標系r。機體坐標系隨著飛機姿態在空中變化而改變。這樣，我們可以使用歐拉角，四元數等來描述r和R之間的角位置關系。經過以上設定，我們已經初步建立了一個四軸飛機的數學模型。

這里我們用歐拉角來描述四軸飛行器的姿態。我們用歐拉角來表示飛機的姿態是直觀的，可以看做飛機繞固定軸的三次旋轉達到現在的姿態。

圖1 繞順序軸旋轉Fig.1 Rotating around a sequential axis

將機體坐標系置于地面坐標系中，我們可以根據空間矢量轉換得到飛行器的姿態。如圖1所示初始狀態為兩坐標原點重合，經過3次平移（沿OX軸平移X，沿OY軸平移Y，沿OZ軸平移Z）和3次轉動（繞OX軸轉動φ，繞OY軸轉動θ，繞OZ軸轉動ψ）到達目標狀態。圖中繞XYZ軸分別對應的名稱為俯仰角（pitch）、翻滾角（roll）和偏航角（yaw），對應上圖中的φ、θ、ψ。按照X-Y-Z順序旋轉來進行分析，導航坐標系與機體坐標系的旋轉矩陣為

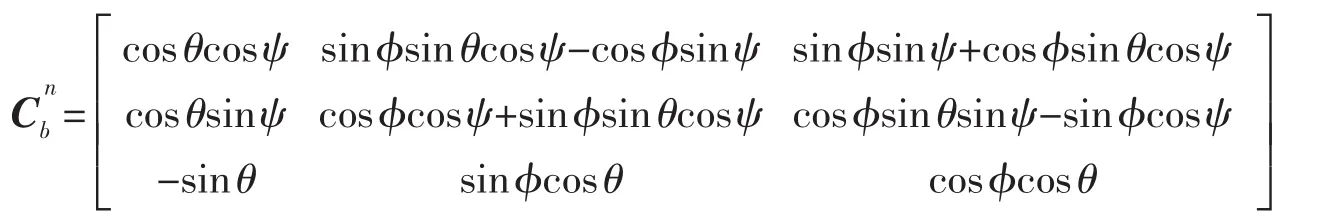
四元數可以描述三維空間中剛體的旋轉，既然四元數可用于描述旋轉，那么就可以用它來描述從導航坐標系R到機體坐標系r，也就是說四元數可以用來描述導航坐標系與機體坐標系的旋轉矩陣。

設描述四旋翼飛行器姿態的四元數[11]為

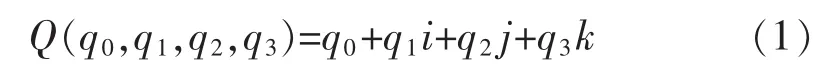
其中四元數q和方向余弦矩陣之間的關系式為

2 互補濾波算法改進

2.1 互補濾波姿態解算算法

先來簡單了解下什么是姿態解算。當某個矢量由不同的坐標系表示時，這個矢量在兩個坐標系中表示的大小和方向肯定是相同的。但是，由于這個旋轉矩陣是由融合前的四元數得到的，只要陀螺儀有積分誤差，這個由四元數得到的旋轉矩陣就會有誤差。當一個矢量經過具有誤差的旋轉矩陣時，就會跟另一個坐標系中的理論值產生偏差。我們通過偏差來糾正這個旋轉矩陣。通過這個過程后，修正四元數以便修正姿態。

由于加速度計的特點是噪聲大，但是不會隨時間積累誤差。而陀螺儀的特點是長期比較穩定，但會有積分誤差，互補濾波器根據它們的特性相互補充，并且每次用加速度計校準以校準陀螺儀。互補濾波是指在短時間內確定陀螺儀經過角速度積分得到的角度作為基礎，并對加速度進行低通濾波并采樣得到的加速度值進行平均，以校正陀螺儀獲得的角度。在短時間內，使用陀螺儀更為準確，長時間使用加速度計會更準確，這時如果增加了加速度計的比例，這就是互補。但這兩個傳感器的數據不能直接使用，因為這兩個傳感器的特性，加速度計需要濾除高頻噪聲，陀螺儀要濾除低頻噪聲。互補濾波器基于傳感器的特性，通過低通或者高通濾波器，然后叉乘得出差值加權補償四元數，以得到較為準確的姿態解算結果。

基于以上論述我們進一步可得到基于四元數互補濾波的傳遞函數和算法步驟：

互補濾波器傳遞函數：

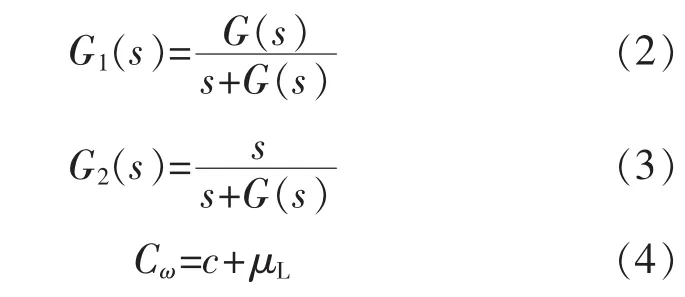
其中

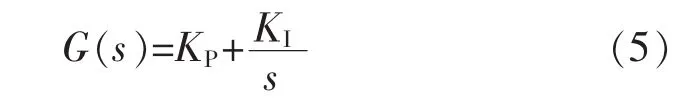
互補濾波的具體步驟為

（1）初始化四元數

姿態解算開始時，將已知載體初始姿態角帶入下式，求出初始時刻四元數。

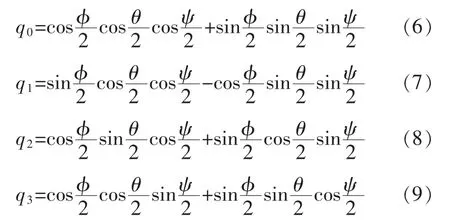
（2）通過傳感器得到角速度，加速度，磁力計值分別讀取加速度計X，Y，Z軸上的測量值ax，ay，az；陀螺儀三軸測量值wx，wy，wz；磁力計三軸測量值mx，my，mz。

（3）將加速度計和磁力計讀取到的數據轉化為單位向量。

（4）從四元數里獲取在機體坐標系下的重力向量：

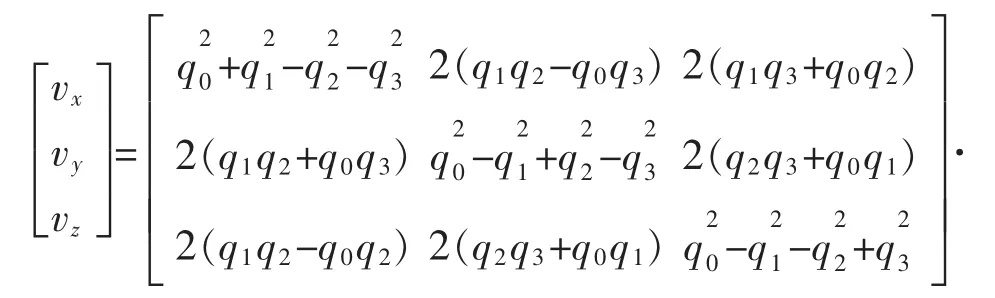
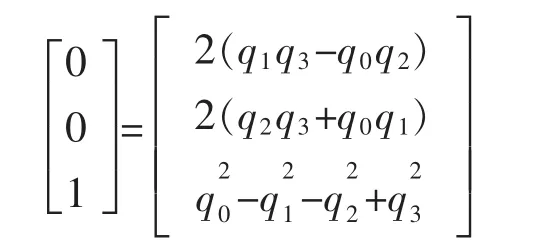
（5）將機體坐標系下的重力向量和機體加速度計測量的重力向量進行叉乘：

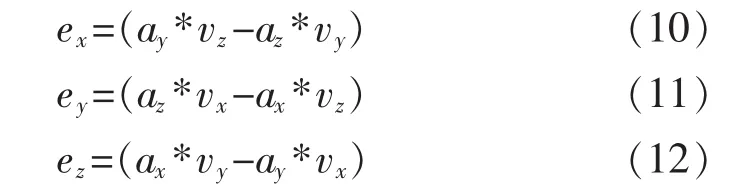
2.2 基于模糊算法的自適應互補濾波估計

針對互補濾波的缺點，既濾波器PI控制器的互補參數kp和ki是固定的情況下很難滿足實現在所有狀態下都能得到最優的系統估計，互補濾波的補充前提條件是加速度計的測量僅僅是重力加速度，所以當飛機的俯仰角和滾轉角很大時，證明飛機正在加速飛行，所以測得的加速度傳感器測量得到的加速度計這個時候就不僅僅是重力加速度還有運動方向的加速度。這些加速度分量都會影響互補濾波的精度。所以這個時候加速度計所測量所得的數據就不能用來校正陀螺儀積分所帶來的誤差或者說減小加速度計校正誤差時的比重。因此引入模糊控制算法目的就在于參數能夠在不同的運動狀態下自適應調節，實現自適應互補濾波，因為在積分項上我們加入了積分分離和積分限幅等算法，所以本文只針對kp進行模糊自適應調節。基本原則就是在大機動大過載的情況下，比例參數能夠自動減小也就是信任陀螺儀多一點，在平穩的時候比例參數增加也就是信任加速度計多一些。

2.3 模糊控制

2.3.1 建立模糊控制規則

隸屬函數圖表示控制中輸入輸出所處的論域區間，如圖2，圖3，圖4所示。控制規則中，本文用E來表示無人機當前時刻姿態角度與零度的偏差，“NB”表示“負角度很大”，“NS”表示“負角度小”，“0”表示“角度 0”，“PB”表示“正角度大”，“PS”表示“正角度小”；用EC來表示無人機當前時刻姿態角的變化率也就是角速度，“NB”表示 “負角速度很大”，“NS”表示“負角速度小”，“0”表示“角速度為 0”，“PB”表示“正角速度大”，“PS”表示“正角速度小”。

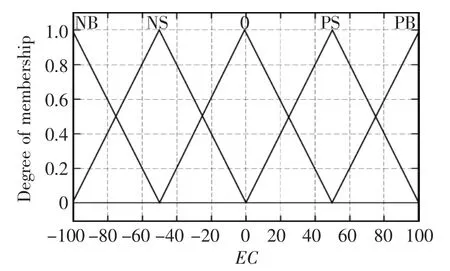
圖2 偏差角變化率隸屬度函數Fig.2 Variation angle change rate membership function

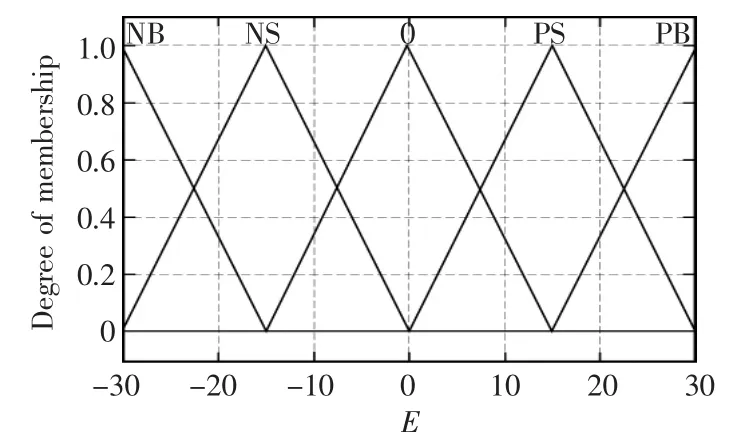
圖3 偏差角隸屬度函數Fig.3 Offset angle membership function

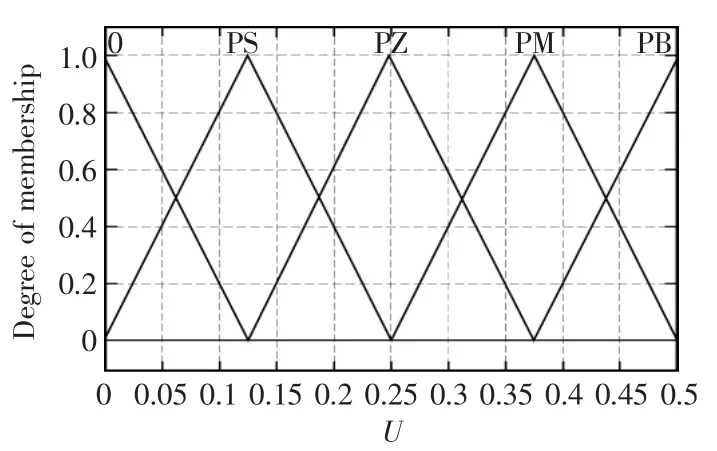
圖4 輸出屬度函數Fig.4 Output membership function

三角形隸屬函數具有計算方便的特點，需要注意的是，所獲得的反模糊是論域的確切值，而不是最終結果，還需要進行去模糊化才能得到實際應用的值。通過這樣的計算的最終結果，才能作為模糊控制。本文選擇通過MIN-MAX-重心法去模糊化。

2.3.2 建立模糊控制規則

建立模糊控制規則的原則就是當無人機在大擾動的情況下即當四旋翼飛行器的俯仰角或者翻滾角大于某一值時陀螺儀的比值占的比例多一點，相反則加速度計占的比例大，當四旋翼飛行器的俯仰角或者翻滾角的角速度在增大的時候陀螺儀的比值增大。相反，當四旋翼飛行器的俯仰角或者翻滾角的角速度在減小的時候，加速度計的比值增大。模糊規則如下如表1所示。

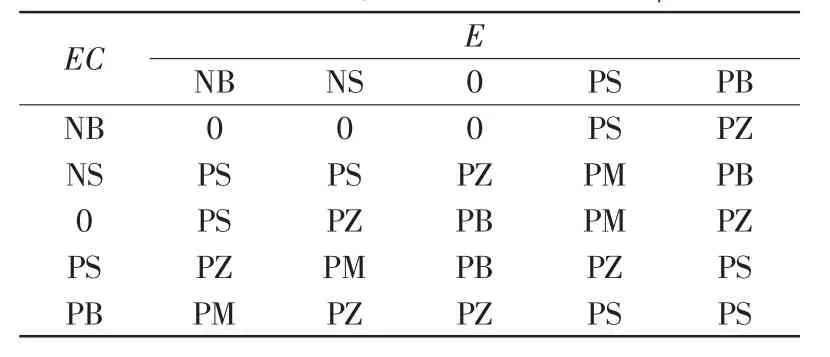
表1 kp模糊規則表Tab.1 Fuzzy rules table of kp

至此，我們得到了模糊控制下的互補濾波算法原理圖見圖5。

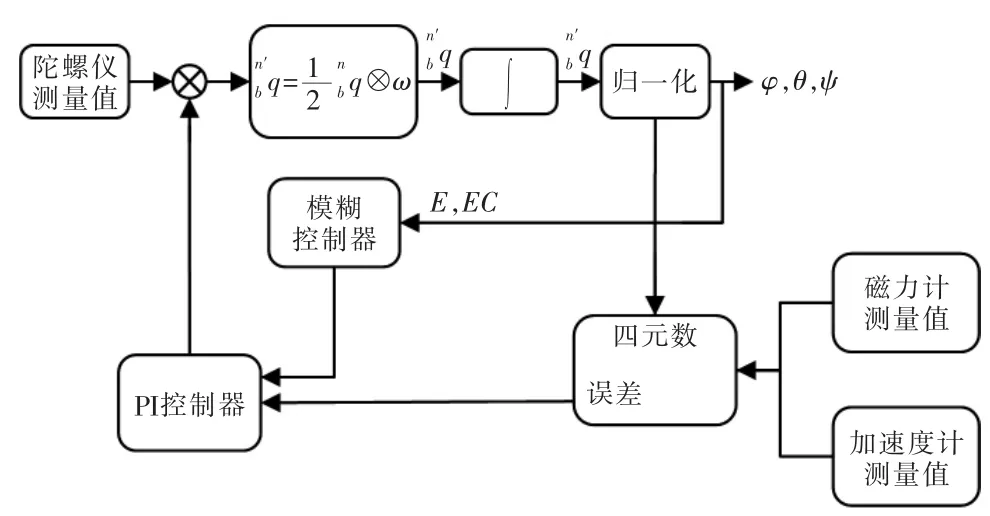
圖5 自適應互補濾波原理圖Fig.5 Adaptive complementary filtering schematic

3 試驗與結果

本文搭建了F450大疆機架的試驗平臺，對角距離為450 mm。為獲得更加靈敏和穩定的飛行效果，飛機采用“X”型飛行模式控制。電調采用好贏40A，電機采用郎宇A2212 980kV的直流無刷電機，槳葉采用ATG 1047槳飛控板為自行設計焊接的飛行控制器。整個飛控代碼工程自行編寫。實物圖如圖6、圖7所示。

IMU慣性導航裝置使用MPU6050傳感器，該裝置包含一個三軸陀螺儀和三軸加速計以支持I2C接口以及一個可編程低通濾波器。本文加上三軸磁力計用于糾正偏航角。但不采用互補濾波算法，所以本文對航向角不做討論。

圖6 四旋翼飛行器實物圖Fig.6 Physical effects of four-rotor aircraft

圖7 四旋翼飛行器室飛行效果圖Fig.7 Flight effect diagram of quadrotor aircraft room

飛行控制單元的主控芯片采用基于ARM Cortex-M4內核的STM32f407。通過該芯片我們軟件模擬I2C，通過硬件SPI接口并且使用通用定時器可輸出PWM波。我們編程輸出400 Hz的PWM波給電機調速器用于電機調速。外部采用8 MHz的外部高速晶振，通過配置寄存器分頻使MCU的工作頻率達到168 MHz，完全可以滿足四軸飛行器的控制。

試驗通過編寫飛控程序給予電調400 kHz頻率的PWM波形，當占空比為1 ms～2 ms時，分別代表油門從0%～100%。陀螺儀輸出信號的低通濾波器的截止頻率為100 Hz，陀螺儀的輸出量程為±2000°/s，更新周期為 0.005 s。翻滾角 PID參數為0.6，0.1，2.2，俯仰角 PID 參數為 0.6，0.1，2.2，偏航角PID 參數為 1.0，0.1，2.0。

試驗采用非加速運動測試和加速運動測試，采樣頻率為5 Hz，數據如圖8、圖9所示。

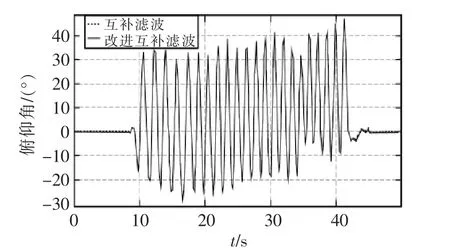
圖8 非加速運動狀態下俯仰角姿態Fig.8 Pitch angle attitude in non-accelerated motion

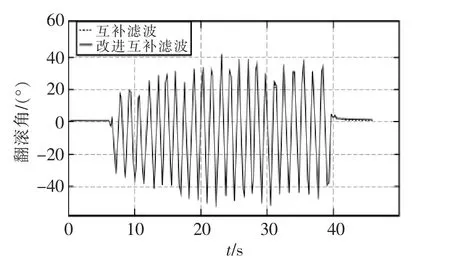
圖9 非加速運動狀態下翻滾角姿態Fig.9 Roll angle attitude in non-accelerated motion

四旋翼飛行器不做水平方向的加速度運動，將飛行器分別繞機體坐標的X軸和Y軸進行轉動，經過一段時間的數據采集，我們發現原始互補濾波得到的姿態角跟改進的互補濾波姿態角幾乎保持一致。都可以很好地解算出機體當前的俯仰角和翻滾角，并且當靜止飛行器的時候兩者都能迅速回歸零度。

接下來我們讓四旋翼飛行器保持一個傾角并進行加速度運動，以此來模擬飛行器空中的加速度飛行。得到一個姿態角數據將其減去四旋翼飛行中保持的傾角度數這樣我們得到一個姿態解算誤差，數據如圖10、圖11所示。

圖10 加速運動狀態下俯仰角姿態誤差Fig.10 Pitch angle gesture in accelerated motion

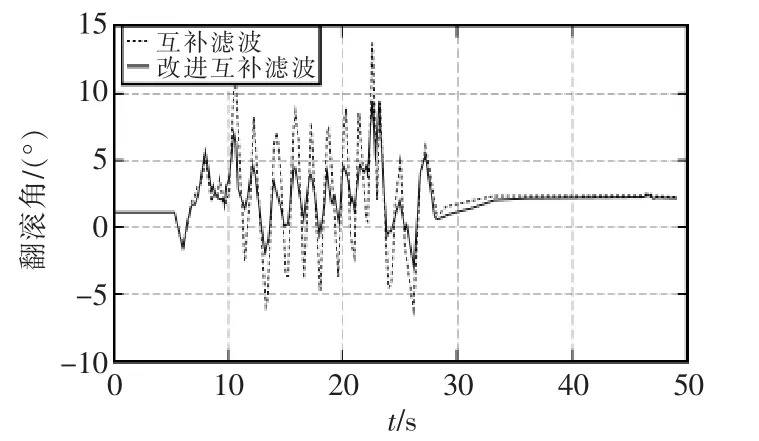
圖11 加速運動狀態下翻滾角姿態誤差Fig.11 Roll angle attitude in accelerated motion

這里我們看俯仰角和橫滾角的姿態解算情況，此時加速度計測得的加速度不再只是重力加速度，還包括水平運動方向上的加速度分量。通過圖我們可以看出原始互補濾波解算出的姿態角較改進的互補濾波解算出的姿態角有較大的誤差。通過比較可以看出，改進的互補濾波解算出的姿態角更為準確。

4 結語

分析了互補濾波姿態計算算法的原理和實現方法。指出了加速度對四旋翼姿態解算計算的影響。在水平加速度較大大時提出了改進的互補濾波算法，指出了互補濾波的限制條件和缺陷。本文設計了一種加入模糊控制的改進互補濾波算法，實現了在四旋翼水平加速運動的狀態下，四旋翼飛行器仍能很好的進行準確的姿態解算。試驗結果表明：該算法提高了姿態計算的準確性，具有良好的實時性。適用于四旋翼飛行器的姿態計算。