基于導向濾波器的超像素分割

劉振國，潘崢嶸，朱 翔

（蘭州理工大學 電氣工程與信息工程學院，蘭州 730050）

隨著計算機視覺的快速發展，在實際應用中圖像處理的速度、精度也越來越高。雖然有圖形處理器 GPU（graphics processing unit）進行加速，但是在多數計算機中計算的實時性仍達不到要求，因而提出了超像素這一概念。

1 超像素及其分割

Ren和Malik在圖像處理中提出超像素的概念，為圖像預處理提供一種全新的設計思路[1]。超像素是指圖像中具有一致特性（相似的紋理、顏亮度等）的像素集。以超像素為處理單元相比以像素為處理單元，具有以下優勢：

1）超像素作為圖像一種緊湊表示方式，不僅可以摒棄冗余的信息而且降低了空間的復雜度。

2）超像素分割將上百萬像素轉換為僅由幾百超像素表示的圖像，這有利于提升計算效率。

3）對于紋理較弱的圖像區域[2]，傳統的方法處理時候難以找到相關的特征點，進而導致這部分信息丟失；而超像素對弱紋理區域信息保存較好。

根據原理的不同，超像素可分為以下2種：①基于梯度的分割，代表算法有Mean Shift算法，Turbo Pixel算法，Watershed 算法，SLIC 算法[3-6]；②基于圖論的分割，代表算法有N-Cuts算法、Superpixel Lattices算法、GCB 與 GCa算法[7-9]。

超像素的分割實質是具有相同屬性的一類像素聚類。傳統的聚類方法有K-mean聚類算法、模糊聚類算法和譜聚類算法等。它們均基于單個像素進行聚類，考慮到其分割結果的不穩定性以及存在較大的噪聲，傳統聚類方法不適合分割的要求。

目前最好的超像素分割算數當屬SLIC（simple liner iterative clustering），它滿足文中圖像分割的要求。因此，文中首先采用導向濾波器對圖像進行預處理，得到邊緣加強的對象，再次使用SLIC對已經處理的圖像進行分割，進而達到提高分割效率的目的。

2 導向濾波器

在導向濾波器[10]的定義中，關鍵的假設是導向圖I與濾波輸出q之間的局部線性模型。假設q是以像素k為中心的窗口Wk中I的線性變換：

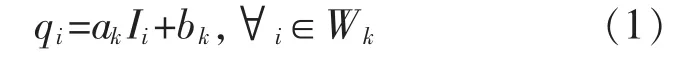
式中：ak和bk為線性模型的系數，在Wk中它們視為常數有用半徑為r的正方形窗口。該線性模型只有在I存在邊的情況下，q才會有邊緣輸出。因為存在的關系為▽q=a▽I，為確定線性系數ak和bk，需要來自濾波輸入p的約束。將輸出q建模為輸入p減去一些不需要的分量n，如噪聲/紋理等。即

為了尋找一種解決方案，在保持線性模型的同時最小化q和p之間的差異，因而最小化在窗口Wk中的代價函數為

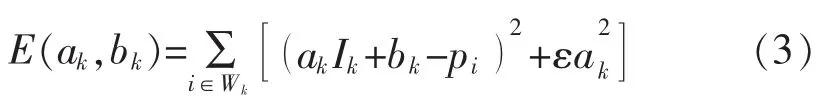
式中：ε為懲罰較大ak的正則化參數。

通過對式（3）的計算，得到的ak和bk計算表達式為

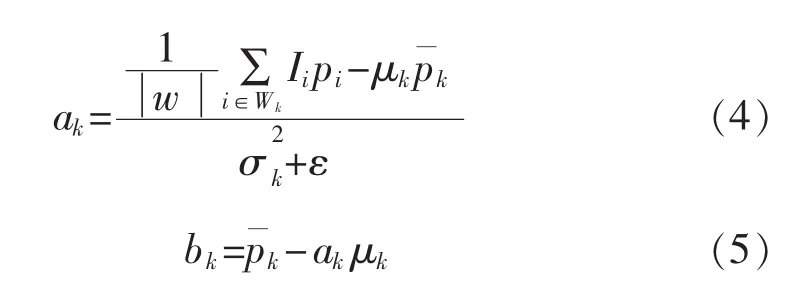
式中：μk和分別為在窗口Wk中I的均值、方差；為窗口Wk中像素的總數。

式中：為窗口Wk中p的均值。由線性系數ak和bk，則可通過式（1）計算得到濾波輸出qi。導向濾波如圖1所示，視差圖紋理與導向圖的一樣，原圖失去了表面紋理。

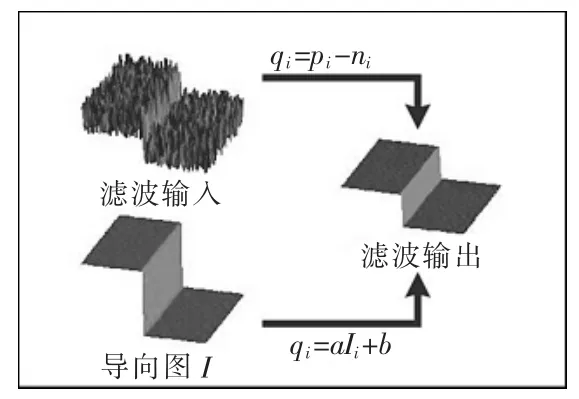
圖1 導向濾波示意Fig.1 Guided filter schematic

由于像素i可能被包含于多個重疊的窗口中，這導致在不同的窗口中用式（1）計算時qi的值不相同，為此采用qi所有可能值的均值來替代。因此在圖像中每個窗口Wk計算ak，bk。

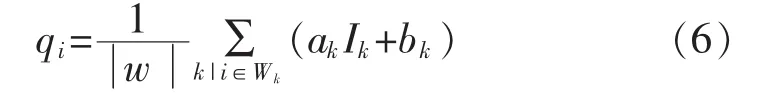
其中

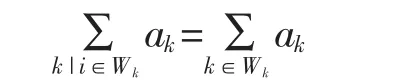
由于盒子窗口的對稱性，式（6）可以重寫為

其中

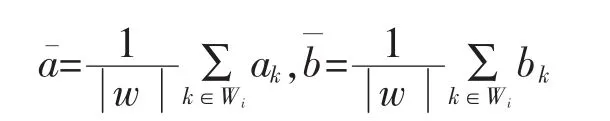
式中：，為所有包含像素i窗口的平均系數。

3 SLIC算法對圖像分割

簡單線性迭代聚類算法SLIC可以產生規則的超像素，并且其在邊界連接、計算效率和分割質量比其他分割算法優異。

SLIC算法是基于K-Means思想提出的一種分割算法，在分割過程中先將RGB圖像轉換到CIE-Lab顏色空間和空間中的五維特征向量然后用生成的五維特征向量來生成像素度量的標準，根據標準進行超像素分割。具體步驟如下：

步驟1獲得種子點并對其進行初始化。根據需要設定分割超像素的個數K，同時在圖內均勻的分配K個種子點。假設處理的圖片I總共有N個超像素，欲得到K個均勻的超像素，則每個超像素大小為N/K，相鄰超像素種子間的距離近似為S=N/K。

步驟2在每個種子點周圍2S×2S的區域進行搜索，找到和種子點相似的若干點進行聚類。由于存在種子點是邊緣或者是噪聲點情況，算法中采用3×3的窗口將種子點沿梯度的方向移動到最小的區域。

步驟3給每個種子點鄰域內的所有像素進行標簽處理。計算每個搜索到的像素點與種子點之間的距離，將像素點分配到與其距離最近的類內。

步驟4重復步驟3直到迭代滿足終止條件為止。

距離的定義為

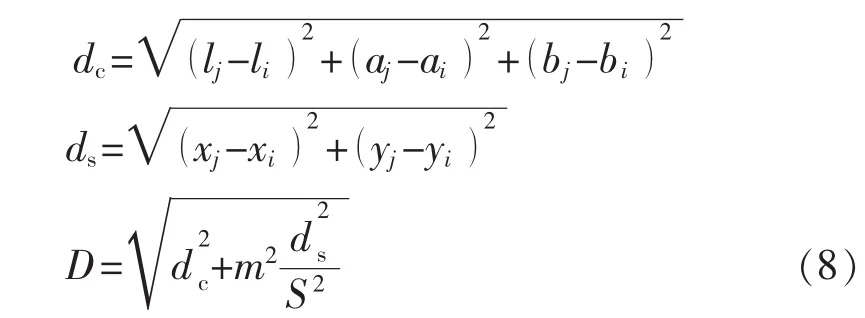
式中：dc為顏色距離；ds為空間距離；S為種子間的距離；m為顏色和空間之間的比例因子，m越大，說明后項占的比例較多，生成的超像素越緊湊；m越小，則說明生成的超像素越不規則。

4 結合導向濾波器與SLIC進行圖像分割

導向濾波器與雙邊濾波器Bilateral Filter一樣，都能起到保護邊緣的作用，但相對于雙邊濾波器，導向濾波器可以更好地接近邊緣并且使邊緣平滑。無論內核、強度大小，導向濾波器是一種快速具有線性的時間算法。因此，文中采用導向濾波器來增強對象的邊緣，對邊緣的像素進行處理。通過使用SLIC算法對導向濾波輸出進行分割。由于導向濾波器對邊緣像素進行了預處理，SLIC在對邊緣像素聚類時減少了迭代次數，使計算效率得到提升。同時，邊緣的強化促使超像素分割的效果相對于僅使用SLIC時的分割更好。超像素分割流程如圖2所示。

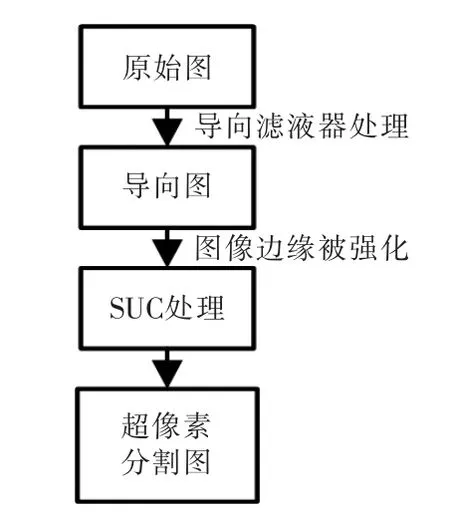
圖2 超像素分割流程Fig.2 Superpixel segmentation flow chart

5 試驗分析

導向濾波器不僅可以平滑對象邊緣，而且更靠近對象的邊緣并對其具有一定強化作用。在此，文中在邊緣強化的部分采用雙邊濾波器Bilateral Filter[11]與導向濾波器進行對比；在超高像素分割部分采用SLIC與文中所提方法（導向濾波和SLIC結合）進行對比。試驗在Intel Core i3 CPU 2.5 GHz的個人電腦上運行，使用Visual Studio 2015和Openc V3.0軟件。

5.1 導向濾波器與雙邊濾波器對比試驗

導向濾波與雙邊濾波的對比如圖3所示，通過對圖3（a）局部區域放大，觀察二者的區別。圖3（b）（d）為導向濾波結果，圖 3（c）（e）為雙邊濾波結果。

由圖 3（b）（d）可見，濾波更接近邊緣，并且邊緣比較平滑；從圖 3（c）（e）可以觀察到，靠近邊緣處的像素并未被正確地處理。由此得出：導向濾波對于對象的邊緣具有增強的效果，其性能優于雙邊濾波。

圖3 導向濾波結果與雙邊濾波結果的對比Fig.3 Comparison between the results of guided filtering and the results of bilateral filtering

5.2 SLIC+原始圖與SLIC+導向圖的對比

文中采用導向濾波與SLIC相結合的程序運行，在代碼的數量上提出的方法較多，無法針對計算效率進行比較。為公平起見，在此僅采用原始圖與導向濾波圖通過SLIC算法處理，對其運行時間及效果進行對比。SLIC+原始圖如圖4所示，SLIC+導向圖如圖5所示。

經過圖4與圖5的對比，可以發現在超像素數為50和100時，盡管都存在對邊緣分割不完善的情況，圖5的效果優于圖4。

圖4 SLIC+原始圖Fig.4 SLIC+the original image

圖5 SLIC+導向圖Fig.5 SLIC+the guided filter image

如超像素數為50時，圖4（b）中箭頭所指的花瓣邊緣明顯沒有被成功分割，而在圖5該部分明顯被分割到邊緣。隨著分割超像素數增大，兩者雖然都能快速接近圖像邊緣，但是圖5的效果稍優于圖4。超像素分割運行時間見1。

表1 超像素分割時間Tab.1 Superpixel segmentation time （s/S）

由表1可知，文中所提方法在超像素分割數量相對較少的情況下，運行的時間相對于SLIC+原始圖的要少，其計算效率有所提升。但隨著分割數量的增加，所提方法比SLIC+原始圖的運行時間長（如超像素數為800時）。這是由于導向圖在保護邊緣的同時，圖像的部分紋理丟失，過小的超像素已不能包含邊緣，因而運行時間較長。由此所提方法在實際應用中超像素數在一定范圍時才能更有效。

6 結語

試驗通過將導向濾波器與SLIC相結合，不僅使圖像的分割更接近對象的邊緣，而且使超像素能夠更好地與對象邊緣對齊。同時，由于將對象的邊緣增強，使在種子點周圍聚類的時候避免了邊緣附近點的干擾，減少了迭代次數從而提高計算效率。該方法不足的之處在于導向濾波處理后，圖像表面的部分紋理丟失，因此不適于對紋理要求較高的地方。