基于模型參考模糊自適應的轉臺摩擦力矩補償研究

姜云翔 王春喜馬 玲 曹雪立 王 茂 趙 健

(1.北京航天計量測試技術研究所，北京 100076；2.哈爾濱工業大學，哈爾濱 150001；3.北京航天控制儀器研究所，北京 100039)

1 引 言

伺服轉臺是一類廣泛應用于航天、航空等領域的精密設備，隨著航天航空技術的高速發展，伺服轉臺的控制性能也需要不斷提高。摩擦干擾力矩的存在嚴重制約著伺服轉臺的控制精度，特別是對于高精度低速伺服轉臺，其摩擦干擾尤其突出。因此必須設計相應的摩擦補償方法對摩擦力矩進行補償。本文以某型雙軸伺服轉臺研制為背景，對其控制系統的設計及摩擦補償技術展開研究，以實現該轉臺承載的光學相機對空間飛行器的快速高精度跟蹤。對抑制摩擦干擾進而提高伺服轉臺的動態跟蹤精度具有一定的理論意義和實用價值。

2 系統模型建立

目前，在工程中經常采用的摩擦模型有庫侖模型、庫侖摩擦+粘滯摩擦模型、靜摩擦+庫侖摩擦+粘滯摩擦模型、Stribeck 摩擦模型、LuGre動態摩擦模型[1]。綜合考慮工程實現難易和對摩擦現象描述的準確性，本文選用可以較為準確地反映摩擦力特性的 Stribeck 摩擦模型。該模型可表示為

(1)

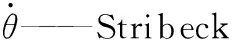
表1 Stribeck模型參數估計

對于直流力矩電機，忽略電樞電感及阻尼系數的影響，建立如圖1所示的數學模型框圖。

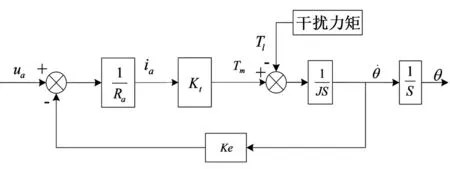
圖1 被控對象數學模型框圖Fig.1 Block diagram of the mathematical model of the controlled object

對應上圖，可以得到實際被控對象的數學模型如式(2)所示。

(2)

不考慮摩擦力矩作用時的系統模型作為標稱模型如式(3)所示。

(3)

系統參數確定如表2所示。

表2 系統參數

3 模型參考模糊自適應

模型參考模糊自適應控制是利用模糊控制器代替常規的、復雜的自適應控制器[2]，該方法并不要求對參考模型和實際被控系統建立精確地數學模型，而只要根據系統的模糊信息，用模糊條件語句寫出控制規則，魯棒性好，實時性好。其控制原理圖如圖2所示。

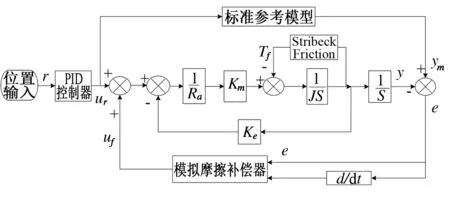
圖2 MRFAC摩擦補償控制原理圖Fig.2 MRFAC principle diagram of friction compensation control

模糊控制器的設計是MRFAC中的核心環節，其需要根據不同的控制對象特征調整模糊控制規則。下面對模糊控制器進行分析設計。模糊控制器的基本結構如圖3所示。

圖3 模糊控制器的基本構成圖Fig.3 Basic composition diagram of fuzzy controller

目前人們廣泛設計和應用二維模糊控制器。設計步驟如下:

(1)確定模糊控制器的輸入、輸出變量

在本摩擦補償控制中，選擇工程中常用的二維模糊控制器，以E、Ec作為模糊推理的輸入，以uf作為摩擦的補償直接作用于實際被控對象。

其中：E——實際系統模型與標準模型的位置誤差；Ec——實際系統模型與標準模型的位置誤差變化率；uf——模糊控制的輸出。

(2)選擇描述模糊控制器輸入和輸出變量的詞集

在本系統中，通過查閱文獻及經驗，選擇七個詞匯描述輸入、輸出變量。即位置誤差E，誤差變化率Ec和模糊推理的輸出uf的模糊詞集均取為：{負大、負中、負小、零、正小、正中、正大}，一般用英文字頭縮寫為{NB，NM，NS，ZO，PS，PM，PB}；在這里取位置誤差E，誤差變化率Ec，模糊推理的輸uf的論域均為{-3，-2，-1，0，1，2，3}。

(3)隸屬度函數

隸屬度函數對模糊控制器的控制效果至關重要，在此，模糊控制器的輸入以及輸出變量均選取S型，三角形、Z型交疊對稱分布的隸屬度函數。曲線如圖4所示。

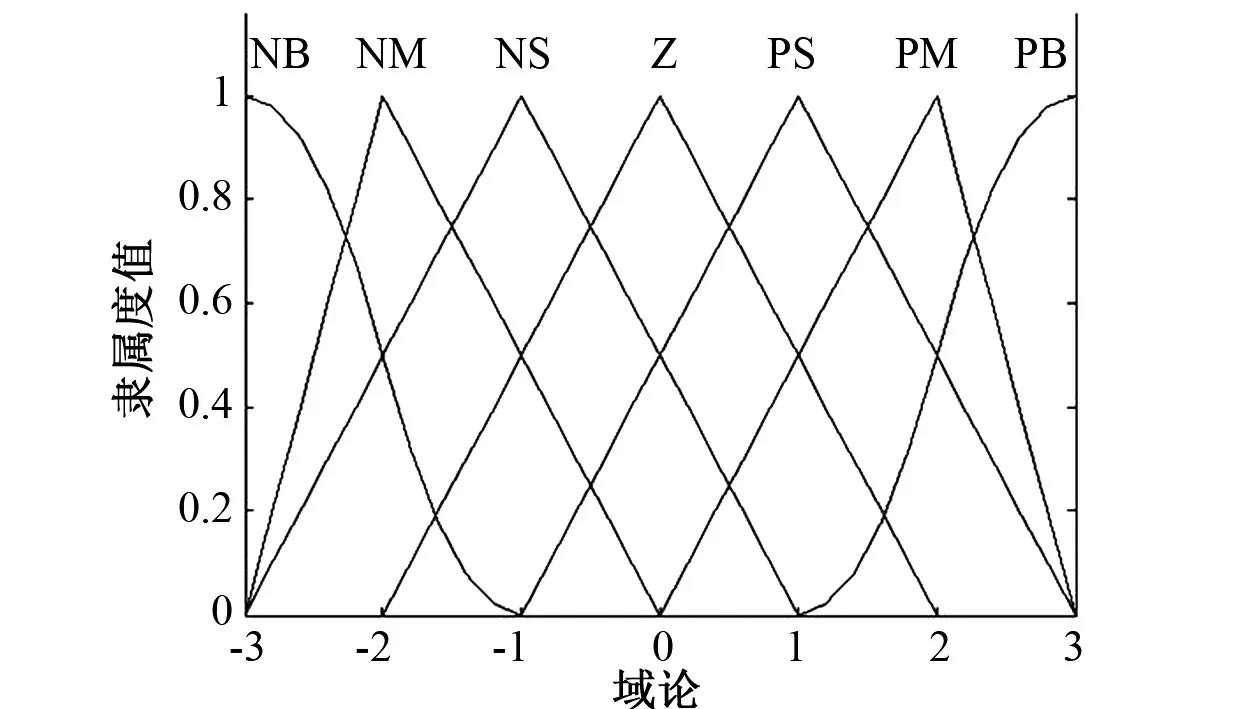
圖4 隸屬度函數曲線Fig.4 Membership function curve

(4)模糊控制規則

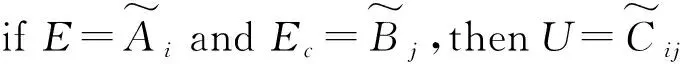
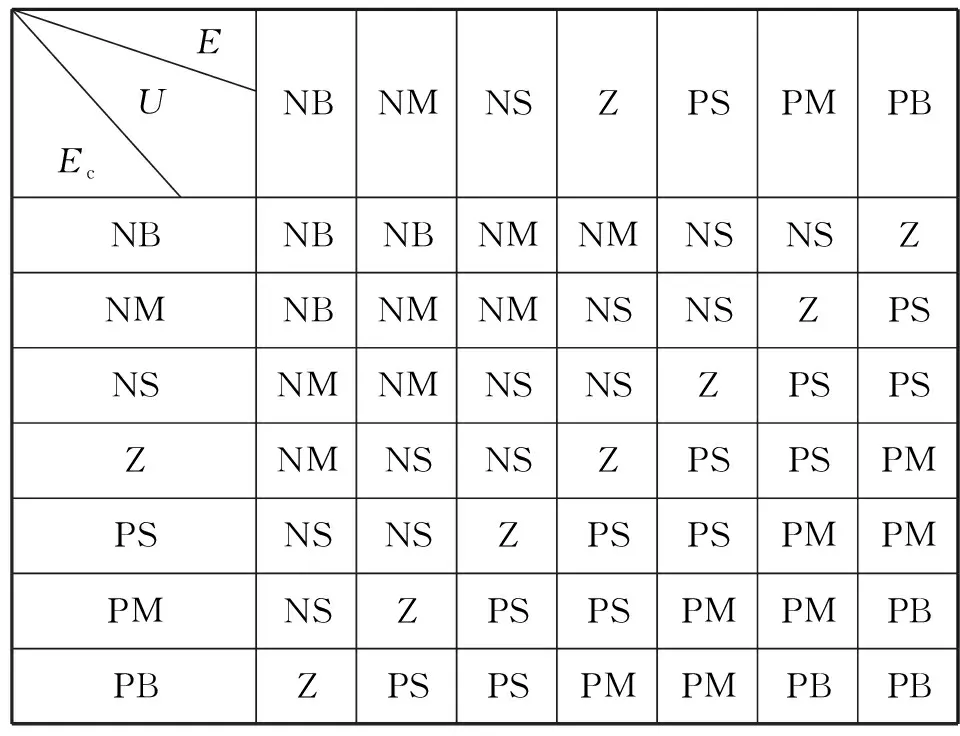
表3 模糊控制規則表

(5)非模糊化方法

通過上述模糊控制規則經過模糊推理得出的控制變量是一個模糊子集，它是一個模糊量而不能直接控制被控對象，還需采用合理的方法將模糊量轉化為精確量，以便最好地發揮模糊推理決策的效果，在本文中，采用面積中心法(centroid)。

(6)量化因子和比例因子的選擇

量化因子和比例因子可以將模糊控制器的輸入變量及模糊控制器的輸出量映射為實際被控系統的輸出誤差和誤差變化量以及其對應的輸入控制量。表示為式(4)。

Ke=n/Xe
Kc=m/Xc
Ku=Yn/l

(4)

式中:Ke——誤差對應的量化因子;Kc——誤差變化對應的量化因子;Ku——控制量對應的比例因子;Xe,Xc——分別為誤差和輸入變量的基本論域最大值;Yn——輸出變量的基本論域最大值;n,m,l——分別為模糊子集。

許多研究者經過實驗證明，在模糊控制器的控制規則及隸屬函數確定的情況下，其量化因子、比例因子的大小以及量化因子之間的相對大小關系，對模糊控制器的控制性能影響極大。因此，在模糊控制器的調試環節，主要是通過對量化因子和比例因子進行調整，確定一組合理的值，從而使系統獲得較好的響應效果。

4 模型參考模糊自適應控制器的穩定性分析

一個控制器的設計首先要保證的是穩定問題，目前常用于分析模糊控制器穩定性的方法有以下幾種：描述函數法、線性近似法、相平面法等[3]。本文選用線性近似法對系統模糊控制器的穩定性進行分析。

將實際被控系統的動態方程，即式(2)表示成如下的狀態方程

(5)

式中:Ap,Bp,Cp——分別為閉環控制系統的狀態轉移陣、控制矩陣以及輸出矩陣。

參考模型的狀態方程表示如下

(6)

式中:Am,Bm,Cm——分別為參考模型閉環系統的狀態轉移矩陣、控制矩陣以及輸出矩陣。u,uf的定義同式(3)中。

式(5)中，模糊控制器和摩擦力矩干擾均為非線性系統，下面分別將其進行近似線性化表示，從而對MRFAC系統進行穩定性分析。

4.1 摩擦模型的線性化

如式(1)所示，Stribeck摩擦模型具有顯著的非線性，對stribeck摩擦函數進行求導得到式(7)，由此確定Stribeck摩擦曲線的走向，這樣能確定更準確的分段線性函數[4,7]。

(7)

(8)

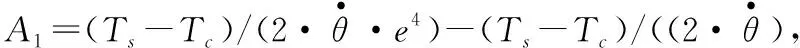
利用Matlab對Stribeck摩擦曲線進行繪制，即式(7)及分段線性函數式(8)描述的曲線，如圖5所示。

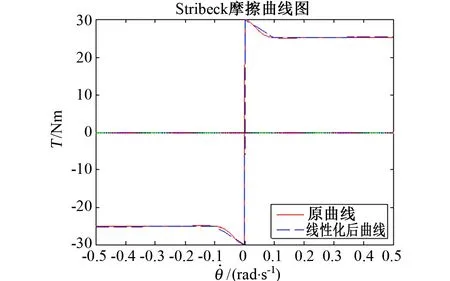
圖5 Stribeck摩擦曲線及其線性化曲線Fig.5 Stribeck friction curve and its linearization curve

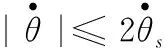
4.2 Lyapunov穩定性證明

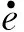
(9)

式中：

(10)

將式(9),式(10)代入式(5)，可得下式

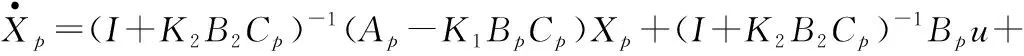
(11)

記Φ=(I+K2B2Cp)-1(Ap-K1BpCp),X0=(I+K2B2Cp)-1Bpu

則式(11)，即被控對象的狀態方程可表示為

(12)

選擇的參考模型是穩定的，則當t→時，有因此，當t→時，(I+K2B2Cp)-1

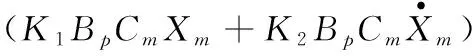
ΦTP+PΦ=-Q

(13)

式中:P,Q——正定實對稱矩陣。由式(13)可以推理保證系統穩定的K1和K2的范圍，用式(14)的不等式表示

α1≤K1≤α2,β1≤K2≤β2

(14)

因此，滿足穩定的模糊控制器輸出u可以表示為如下的不等式

(15)

當模糊控制器輸出滿足式(15)時，則能證明該控制系統穩定。

由式(15)可以看出，模糊控制器輸出在一定范圍內變化，正是由于這種輸出的動態調整作用，才使得模型參考模糊自適應系統具有較強的自適應能力，從而對復雜控制模型具有較好的控制效果。

5 實驗結果分析

為了驗證上述摩擦補償方法的效果,本文進行了數值仿真。選取參考輸入的位置信號為

θd=Asin(2πft)

(16)

式中:A——位置信號的幅值，取A=2；f——位置信號的變化頻率，取f=0.16Hz；t——時間。

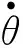
圖6 未補償位置跟蹤曲線Fig.6 Uncompensated position tracking curve

圖7 未補償速率跟蹤曲線 Fig.7 Uncompensated velocity tracking curve

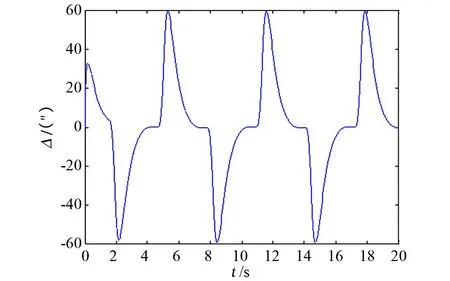
圖8 未補償位置跟蹤誤差曲線Fig.8 Uncompensated position tracking error curve

從未進行摩擦補償的曲線可以看出，受摩擦力矩的影響，位置跟蹤曲線有明顯的“平頂”現象，速率跟蹤曲線有死區現象，位置跟蹤偏差大；而從進行摩擦補償的曲線可以看出，其位置跟蹤曲線的“平頂”現象及速率跟蹤的“死區”現象均有明顯改善，且位置跟蹤偏差顯著下降至10″以內，提高了轉臺的伺服精度。

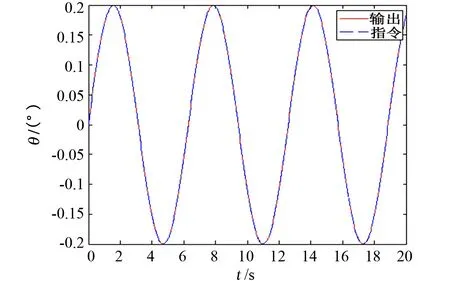
圖9 補償后位置跟蹤曲線Fig.9 Position tracking error curve after compensated

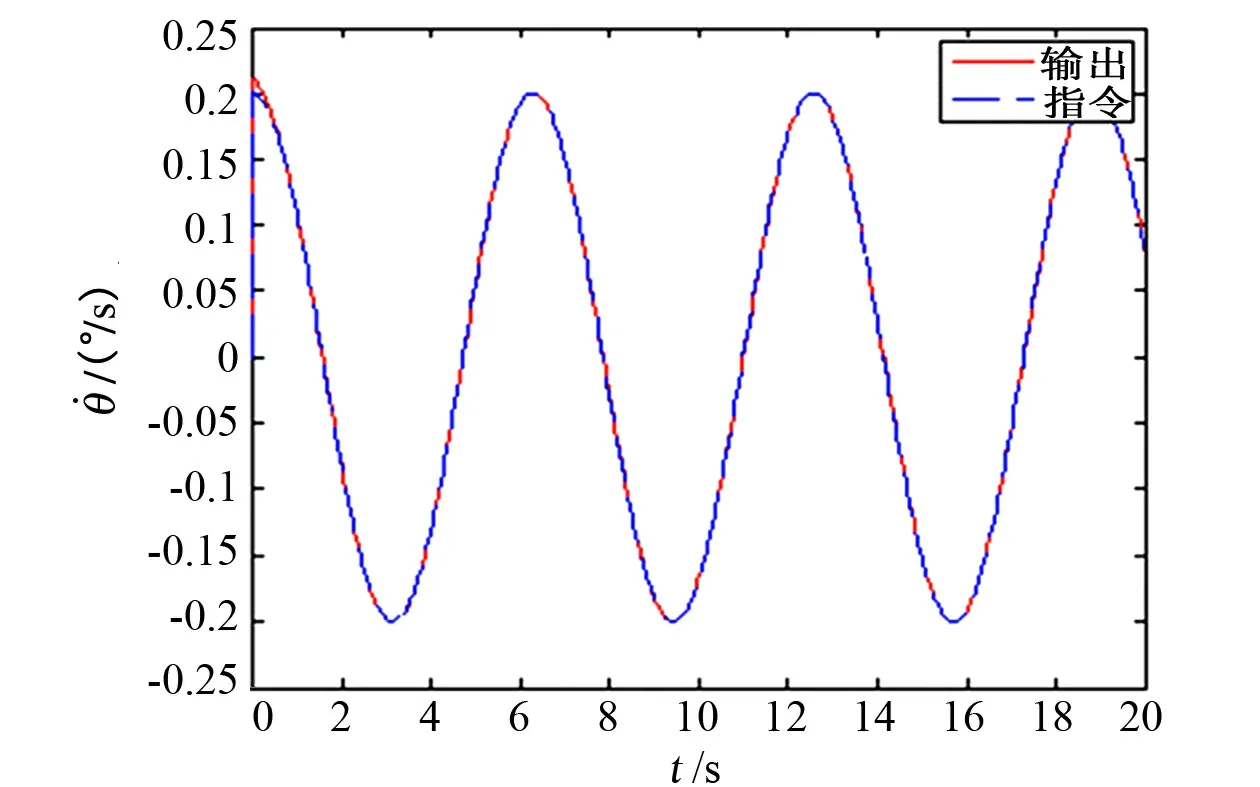
圖10 補償后速率跟蹤曲線Fig.10 Velocity tracking curve after compensated

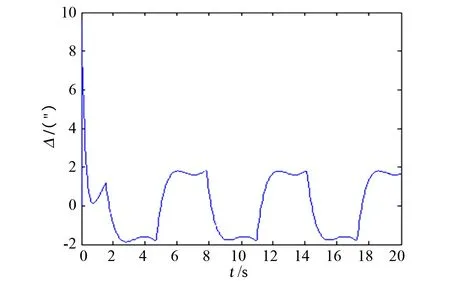
圖11 補償后位置跟蹤誤差曲線Fig.11 Velocity tracking error curve after compensated

6 結束語

針對某型伺服轉臺在摩擦力矩干擾下引起的低速爬行問題，本文設計了基于模型參考模糊自適應方法的摩擦力矩補償控制方案，并進行了穩定性分析以及仿真論證。仿真結果表明，該摩擦補償方法能夠有效抑制摩擦干擾的不利影響，顯著提高了轉臺的伺服精度。