鋼管混凝土格構(gòu)式新型風(fēng)力發(fā)電機塔架風(fēng)振響應(yīng)

李 斌，文昊天，高春彥

（內(nèi)蒙古科技大學(xué) 土木工程學(xué)院土木工程系，內(nèi)蒙古 包頭 014010）

風(fēng)力發(fā)電單機容量的不斷增大使得應(yīng)用于大型風(fēng)電機組的傳統(tǒng)塔架結(jié)構(gòu)安全性越來越低[1]，風(fēng)電事故時有發(fā)生。當(dāng)風(fēng)力發(fā)電機塔筒超過一定高度后，其結(jié)構(gòu)的力學(xué)性能下降非常明顯，主要表現(xiàn)在：塔頂在水平荷載作用下變形過大，塔身與上部風(fēng)機產(chǎn)生共振，塔身容易發(fā)生疲勞破壞[2]。塔架是風(fēng)力發(fā)電機組的主要承載結(jié)構(gòu)，不但要承受機艙重量、風(fēng)輪作用力以及風(fēng)對塔架的彎、剪、扭等靜力作用，還要承受振動作用力[3]。而且鋼制高聳結(jié)構(gòu)對局部缺陷十分敏感，其臨界承載力只能達(dá)到理論值的1/5～1/3，很容易發(fā)生失穩(wěn)破壞[4]。塔架是為風(fēng)力發(fā)電機組正常工作服務(wù)的結(jié)構(gòu)，其發(fā)展水平應(yīng)與風(fēng)力發(fā)電機組的發(fā)展相協(xié)調(diào)。為了滿足現(xiàn)代風(fēng)力發(fā)電機的工作需求，必須要保證塔架在風(fēng)荷載作用下的安全。

根據(jù)各國風(fēng)機受損的歷史統(tǒng)計數(shù)據(jù)，塔架是風(fēng)機受損部件中遭受破壞比率較大的部件之一，占到19%[5]。從功能性角度來看，塔架是風(fēng)電機組中重要的支撐結(jié)構(gòu)，為風(fēng)力發(fā)電機提供必要的工作高度；從荷載角度來看，塔架的重量占到風(fēng)機總重的1/2左右；從經(jīng)濟(jì)性角度來看，塔架的成本大約為整個風(fēng)機制造總成本的15%左右，而且塔架倒塌必定造成風(fēng)力發(fā)電機的損傷[6]。因此，鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架在風(fēng)荷載作用下動力響應(yīng)的研究對于提高塔架的設(shè)計水準(zhǔn)、保證風(fēng)機的運行安全和整機性能都有重要意義。

1 風(fēng)速時程模擬

對本文所采用的鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架不同高度處的13個計算點進(jìn)行風(fēng)速時程模擬，計算點位置選取如圖1所示。

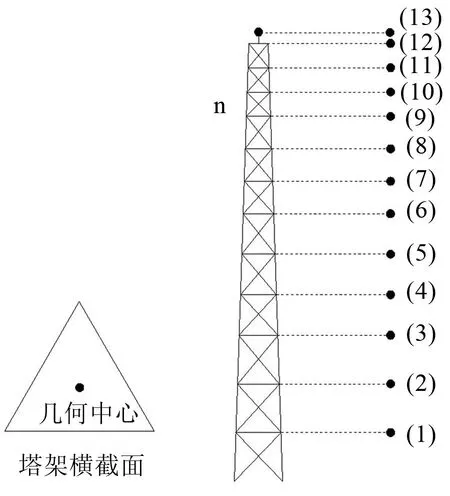
圖1 塔架橫截面與計算點位置示意圖

其中13號節(jié)點為風(fēng)輪中心位置。選取我國規(guī)范所采用的Davenport脈動水平風(fēng)速譜以及Shiotami的簡化空間相關(guān)性系數(shù)表達(dá)式。為了得到較為準(zhǔn)確的脈動風(fēng)速時程曲線，采用諧波合成法對塔架工作地區(qū)的脈動風(fēng)進(jìn)行風(fēng)速時程模擬；為了得到更準(zhǔn)確的平均風(fēng)速，以對數(shù)律求解平均風(fēng)速廓線。具體模擬參數(shù)如表1所示。

表1 風(fēng)速時程模擬參數(shù)

借助MATLAB軟件編寫程序，最終生成各計算點的風(fēng)速時程曲線。

2 風(fēng)力發(fā)電機塔架有限元模型建立

本文所采用的2 MW風(fēng)力發(fā)電機塔架高度為60 m，風(fēng)機轉(zhuǎn)子中心高度為61.5 m。塔架分12層，層高有4 m、5 m和6 m三種。應(yīng)用ABAQUS軟件建立鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架有限元模型，鋼管模型采用殼單元，混凝土模型采用實體單元。將鋼管與混凝土的接觸定義為剛體約束，忽略鋼管與混凝土在受力過程中的局部滑移。將所有焊接節(jié)點設(shè)置為綁定約束，另外忽略風(fēng)力發(fā)電機塔架的基礎(chǔ)與地基土之間復(fù)雜的相互作用，將之視為剛性連接。為了提高網(wǎng)格質(zhì)量，對裝配件整體布種，對不同單元分別指派網(wǎng)格控制屬性。在分析步中設(shè)置頻率分析步，提取塔架的各階頻率和振型，用于后續(xù)風(fēng)振響應(yīng)計算。

圖2 風(fēng)力發(fā)電機塔架有限元模型

3 風(fēng)力發(fā)電機塔架風(fēng)致響應(yīng)分析

由模擬得到的各個計算點風(fēng)速時程曲線求解對應(yīng)的風(fēng)荷載時程曲線，利用ABAQUS有限元軟件將風(fēng)荷載以節(jié)點力的形式作用于塔架模型對應(yīng)的計算點，分析得到鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架各計算點的位移、速度和加速度響應(yīng)曲線。

3.1 塔架風(fēng)輪中心位置處的風(fēng)振響應(yīng)

提取風(fēng)輪中心位置處的位移、速度和加速度響應(yīng)時程曲線分別如圖3、圖4、圖5所示。

圖3 13號節(jié)點位移響應(yīng)時程曲線

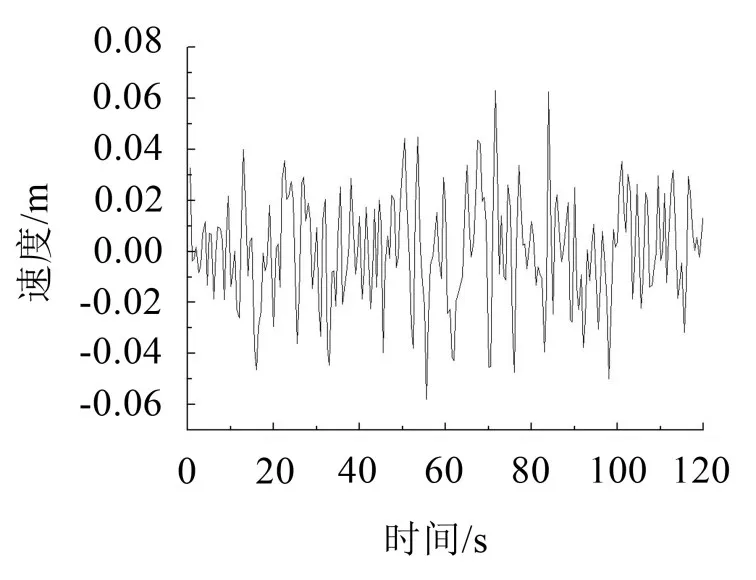
圖4 13號節(jié)點速度響應(yīng)時程曲線

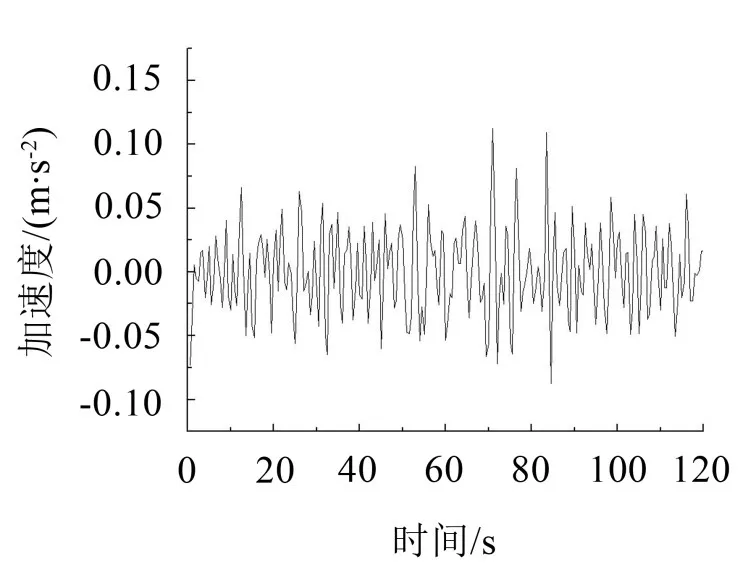
圖5 13號節(jié)點加速度響應(yīng)時程曲線

從圖3可以看出，塔架風(fēng)輪中心位置處的順風(fēng)向位移在0.07 m～0.23 m之間，位移響應(yīng)峰值為0.23 m，平衡位置與初始位置的水平距離約為0.17 m，在模擬的時段內(nèi)13號節(jié)點位置處的位移響應(yīng)表現(xiàn)出很強的隨機性。

由圖4可知13號節(jié)點的速度響應(yīng)在±0.06 m/s之間，大部分時間處于±0.02 m/s之間，速度峰值響應(yīng)為0.06 m/s。

由圖5可知，風(fēng)輪中心位置處加速度峰值響應(yīng)為0.11 m/s2，同樣也表現(xiàn)出極強的隨機性和波動性。

3.2 塔架整體風(fēng)振響應(yīng)

從表2可以看出隨著高度的增加，結(jié)構(gòu)的位移響應(yīng)均值、位移響應(yīng)極值以及加速度響應(yīng)均方差都在增加。

位移響應(yīng)極值與位移響應(yīng)均值的差距逐漸增大，脈動風(fēng)對結(jié)構(gòu)位移響應(yīng)的作用是隨高度不斷增加的。在61.5 m高度處脈動風(fēng)位移響應(yīng)分量已接近總風(fēng)響應(yīng)的30%。

圖6、圖7所示分別為鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架各節(jié)點位移的響應(yīng)均值和加速度響應(yīng)的均方差隨塔架高度變化的關(guān)系。

從圖中可以看出位移響應(yīng)均值和加速度響應(yīng)均方差隨高度的增加逐漸變大，且變化速度越來越快。這主要是因為隨著高度的增加結(jié)構(gòu)的橫截面面積減小、剛度下降而荷載反而增大所引起的。

圖6 塔架位移響應(yīng)均值

圖7 塔架加速度響應(yīng)均方差

為了研究不同風(fēng)速工況下鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架的風(fēng)振響應(yīng)，在不改變其他參數(shù)的條件條件下，分別取vˉ10=10 m/s、20 m/s、25 m/s、30 m/s對塔架的8號節(jié)點和13號節(jié)點進(jìn)行風(fēng)振響應(yīng)計算。

圖8中就風(fēng)力發(fā)電機塔架8號節(jié)點和13號節(jié)點在不同風(fēng)速工況下的加速度響應(yīng)均方差進(jìn)行了比較。從圖中可以看出節(jié)點的風(fēng)振響應(yīng)隨著基本風(fēng)速的增加單調(diào)增加。節(jié)點加速度響應(yīng)均方差在10 m/s～20 m/s的風(fēng)速范圍內(nèi)增長較為緩慢，在20 m/s～25 m/s的風(fēng)速范圍內(nèi)增速明顯增大，之后又有所下降。相比之下，高度越高，風(fēng)振響應(yīng)對風(fēng)速的變化越敏感。

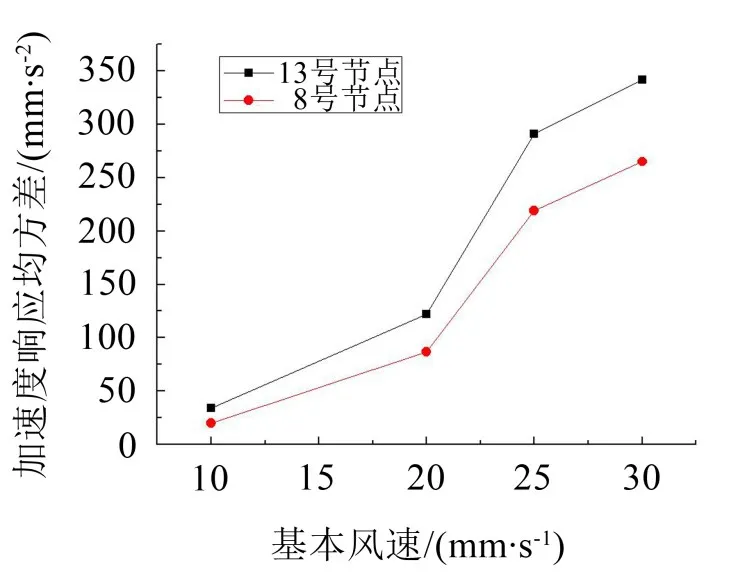
圖8 不同風(fēng)速工況下節(jié)點加速度響應(yīng)均方差

不同結(jié)構(gòu)形式的阻尼比取值不同，阻尼比會影響動力時程計算的結(jié)果。為了分析不同阻尼比對塔架風(fēng)振響應(yīng)的影響，取基本風(fēng)速其他參數(shù)保持不變，分別取阻尼比ζ=0.02、0.035、0.05，計算塔架8號節(jié)點與13號節(jié)點的加速度響應(yīng)時程。

由圖9可以看出，節(jié)點的風(fēng)振響應(yīng)隨著阻尼比的增大而減小。在鋼管中灌入混凝土可以提高結(jié)構(gòu)的阻尼比，在一定程度上達(dá)到減振的目的。

圖9 不同阻尼比時節(jié)點加速度響應(yīng)均方差

4 塔架順風(fēng)向風(fēng)振系數(shù)

4.1 塔架結(jié)構(gòu)分段

本文研究的鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架為高聳結(jié)構(gòu)，為保證準(zhǔn)確性，對風(fēng)振系數(shù)的分析和計算必須分段進(jìn)行。

如圖10所示，將鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架沿高度方向分為6段。

各塔段結(jié)構(gòu)參數(shù)如表2所示，其中迎風(fēng)面寬度為各塔段二分之一高度處的迎風(fēng)面寬度。

4.2 不同方法中的風(fēng)振系數(shù)計算

計算所選參數(shù)見表3至表7。

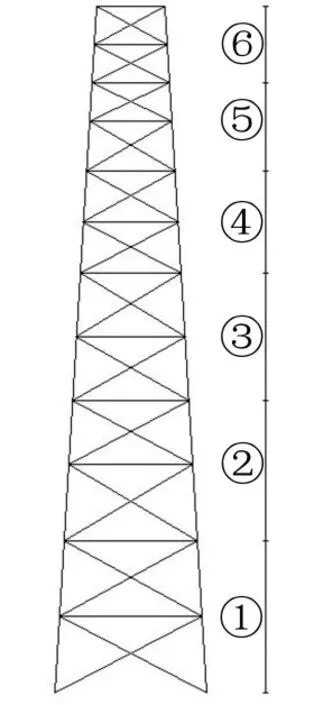
圖10 塔架分段圖

4.3 結(jié)果分析

將上一節(jié)中按照四種不同方法計算得到的風(fēng)振系數(shù)進(jìn)行比較，見圖11。

圖11 不同方法計算所得的風(fēng)振系數(shù)對比

從圖中可以看出，基于隨機振動理論按Davenport譜和按時程分析結(jié)果所得到的風(fēng)振系數(shù)基本吻合。在按隨機振動理論計算塔架響應(yīng)時只取了第1階振型，這表明基于隨機振動理論計算鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架風(fēng)振系數(shù)只取第1階振型進(jìn)行計算是可行的。因為只取了起控制作用的第1階振型，隨機振動理論的計算值較數(shù)值模擬結(jié)果略微偏低。

表3 鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架各塔段結(jié)構(gòu)參數(shù)

表4 基于Davenport風(fēng)譜計算所得的風(fēng)電塔架風(fēng)振系數(shù)

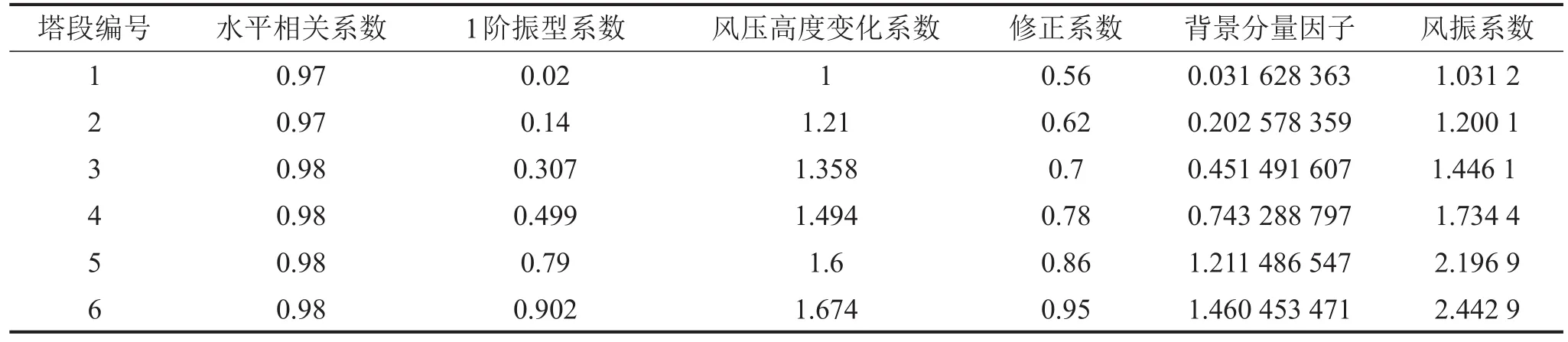
表5 基于《建筑結(jié)構(gòu)荷載規(guī)范》（GB50009-2012）計算所得的風(fēng)電塔架風(fēng)振系數(shù)

表6 基于《高聳結(jié)構(gòu)設(shè)計規(guī)范》（GB50135-2006）計算所得的風(fēng)電塔架風(fēng)振系數(shù)

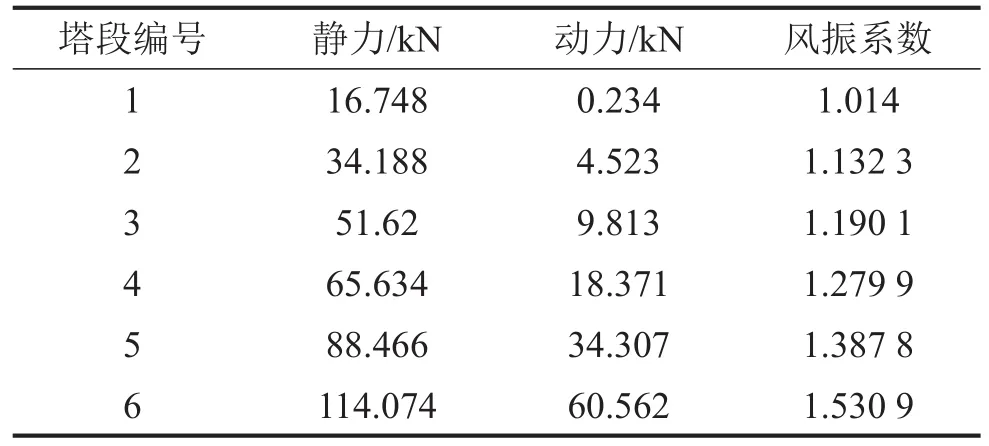
表7 基于數(shù)值分析結(jié)果計算所得的風(fēng)振系數(shù)

按照《高聳結(jié)構(gòu)設(shè)計規(guī)范》（GB50135-2006）計算所得的風(fēng)振系數(shù)與數(shù)值模擬的結(jié)果相比較，在50 m以下尚可，超過50 m以后出現(xiàn)了偏低的情況，這對結(jié)構(gòu)的安全性是不利的。現(xiàn)行《高聳結(jié)構(gòu)設(shè)計規(guī)范》（GB50135-2006）計算參數(shù)少，計算便利，但參數(shù)的物理意義不夠明確，且針對不同結(jié)構(gòu)形式的參數(shù)選用描述模糊、不夠全面，在確定系數(shù)時往往需要自行插值計算，受主觀影響較大。

按照《建筑結(jié)構(gòu)荷載規(guī)范》（GB50009-2012）計算所得的風(fēng)振系數(shù)與數(shù)值模擬的結(jié)果吻合度最差。新版《建筑結(jié)構(gòu)荷載規(guī)范》（GB50009-2012）關(guān)于風(fēng)振系數(shù)計算的參數(shù)設(shè)置較為詳細(xì)，每個參數(shù)的物理意義清晰，但對于鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架這種結(jié)構(gòu)形式來說計算結(jié)果過于保守，并不十分適用。

5 結(jié)語

（1）在基本風(fēng)速為29.94 m/s時，鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架頂點的脈動風(fēng)位移響應(yīng)分量接近總位移響應(yīng)的30%，風(fēng)振響應(yīng)顯著，脈動風(fēng)對結(jié)構(gòu)響應(yīng)影響很大。

（2）結(jié)構(gòu)的風(fēng)振響應(yīng)與風(fēng)速和結(jié)構(gòu)的阻尼比相關(guān)，它隨著風(fēng)速的增加而增加，隨著結(jié)構(gòu)阻尼比的增加而減小。鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架結(jié)構(gòu)阻尼比較純鋼結(jié)構(gòu)塔架大，具有更好的抗風(fēng)振能力。

（3）現(xiàn)行《建筑結(jié)構(gòu)荷載規(guī)范》（GB50009-2012）和《高聳結(jié)構(gòu)設(shè)計規(guī)范》（GB50135-2006）提供的風(fēng)振系數(shù)計算方法對于新型鋼管混凝土格構(gòu)式風(fēng)力發(fā)電機塔架并不適用，誤差較大。