高中物理圖像中“面積”的意義和應(yīng)用

(江蘇省啟東中學(xué)，江蘇 南通 226200)

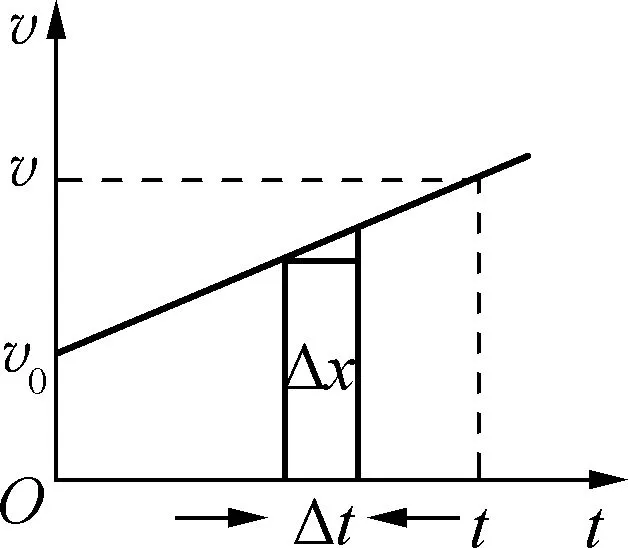
圖1

高中物理中第一次接觸到圖像“面積”的意義,是在推導(dǎo)勻變速直線(xiàn)運(yùn)動(dòng)位移與時(shí)間關(guān)系時(shí),教材中利用“微元法”說(shuō)明v-t圖像中圖線(xiàn)與橫軸包圍的“面積”表示位移。圖1為一勻變速直線(xiàn)運(yùn)動(dòng)的v-t圖像,當(dāng)把時(shí)間分割為無(wú)限個(gè)無(wú)限小的時(shí)間元Δt,每一個(gè)Δt時(shí)間內(nèi)可以認(rèn)為物體做勻速運(yùn)動(dòng),則小矩形的“面積”可表示該段時(shí)間內(nèi)物體的位移元Δx,然后對(duì)這些位移元求和,就可以用圖線(xiàn)與坐標(biāo)軸包圍的梯形“面積”來(lái)表示t時(shí)間內(nèi)物體的位移。這種利用微元法處理,看圖線(xiàn)與橫軸包圍“面積”的方法,還適用于a-t、F-t、P-t、i-t、F-x、E-x、p-V圖像，現(xiàn)將高中階段常見(jiàn)的圖形的“面積”的意義總結(jié)如下。

1 v-t圖像中圖線(xiàn)與橫軸包圍的“面積”表示位移

例1：某同學(xué)欲估算飛機(jī)著陸時(shí)的速度,他假設(shè)飛機(jī)在平直的跑道上做勻減速運(yùn)動(dòng),飛機(jī)在跑道上滑行的距離為x,從著陸到停下來(lái)所用的時(shí)間為t。實(shí)際上,飛機(jī)的速度越大,所受的阻力也越大,則飛機(jī)著陸時(shí)的速度應(yīng)是( )。

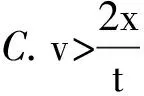
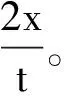
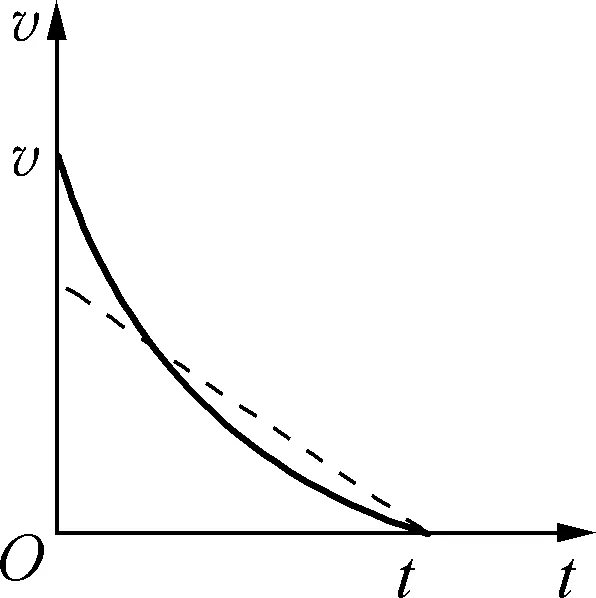
圖2

2 a-t圖像中圖線(xiàn)與橫軸包圍的“面積”表示速度變化量

例2：一質(zhì)量為2kg的物體受水平拉力F的作用,在粗糙水平面上做加速直線(xiàn)運(yùn)動(dòng)時(shí)的a-t圖像如圖3所示,t=0時(shí)其速度大小為2m/s,滑動(dòng)摩擦力大小恒為2N,求0～6s內(nèi)合力的功和6s時(shí)拉力的瞬時(shí)功率。

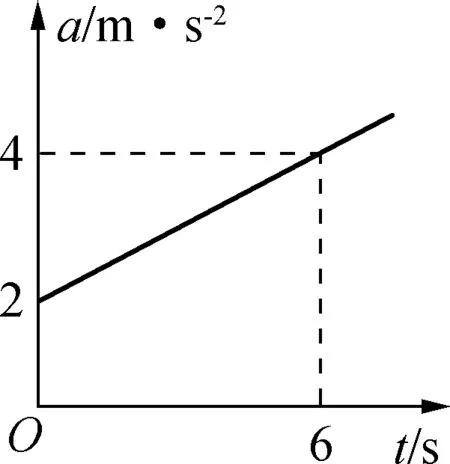
圖3

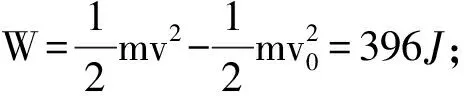
3 F-t圖像中圖線(xiàn)與橫軸包圍的“面積”表示沖量

例3：原來(lái)靜止的物體受合外力作用時(shí)間為2t0,作用力隨時(shí)間變化情況如圖4所示,求0～2t0時(shí)間內(nèi)合外力的功和合外力的沖量。

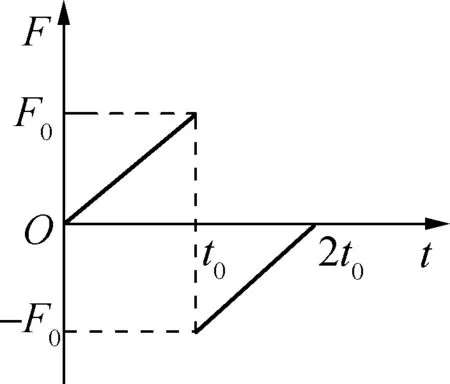
圖4

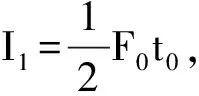
4 i-t圖像中圖線(xiàn)與橫軸包圍的“面積”表示電量

例4：如圖5所示為一電流隨時(shí)間的變化圖像,求電流的平均值。……