兩種概率分析方法的混凝土疲勞壽命模型比較

(鄭州工業應用技術學院 河南 新鄭 451100)

引言

自從1829年德國采礦工師W.A.J.Albert提出第一個疲勞問題研究報告以來，人們對疲勞問題的研究已經持續將近兩個世紀，但仍有許多問題困擾著人們。其中，因混凝土自身為非均質多相材料，在靜力作用下其相關性質的離散度就較大，而且在疲勞荷載等動力作用下，其相關性質的離散度就更大，由此產生一系列難題。如試件制備方法、試驗方法、試驗數據處理方法等。針對混凝土疲勞問題，主要對一定強度等級的混凝土，在一定疲勞應力水平下的S-N曲線、ε-N曲線、σ-ε曲線等特征參數進行試驗研究，然后再針對試驗數據進行相關理論分析。在對材料諸多疲勞行為的研究中，材料的疲勞壽命曲線是預測結構疲勞壽命和進行結構抗疲勞設計的基礎。目前，常用的材料疲勞壽命曲線有兩類：應力-壽命(S-N)曲線和應變-壽命(ε-N)曲線。材料的疲勞壽命曲線的表述形式可采用表格形式或表達式形式，而在理論研究和工程應用中，為準確反映物理規律以及使用方便，通常采用表達式形式。譬如，因混凝土試件靜載強度的離散性導致疲勞應力水平S的離散性加大，又進一步導致疲勞壽命N的離散性更大；類似的參數還有應變、彈性模量等，其離散性均為逐步放大。因此，S-N等曲線的這種固有缺陷是無法從根本上消除的，這就需要利用相關數學手段對試驗數據進行有效分析，來提高混凝土疲勞壽命的預測精度。在1939年之前，對混凝土疲勞壽命的概率分析，基本上都是采用對數分布[1-3]或對數正態分布[4]。但在1939年，瑞典人Weibull提出了一種描述材料疲勞強度的分布模型，即Weibull分布模型[5,6]。該模型參數能較好地反映隨機荷載下機械產品及其零件的疲勞壽命和疲勞強度。而在1956年，Leiblein和Zenlen在對滾珠軸承的疲勞試驗分析時即用到了Weibull分布。此后，Weibull分布便被廣泛應用于零部件的疲勞分析，以及后來的可靠性分析之中。經過多年來國內外廣大學者[7-9]的深入系統地研究，不僅證明了混凝土疲勞壽命既服從對數正態分布又服從兩參數Weibull分布，并通過概率函數研究了這兩種函數的逼近性；而且基于工程可靠性的Weibull分布模型，對混凝土的疲勞壽命預測更加合理。為此，本文通過相關文獻中的試驗數據，對提高疲勞壽命預測精度的方法進行了系統分析，結果證明該方法是正確的。

一、結構可靠度理論[10-12]

結構的可靠性是指結構在規定的時間內，在規定的條件下，完成預定功能的能力。假設結構或構件能完成預定功能(Z≥0)的概率稱為可靠概率，亦稱為可靠度(ps)，而不能完成預定功能的概率(Z<0)，則稱之為失效概率(Pf)。又假設功能函數(Z)僅與作用效應(S)和結構抗力(R)兩個基本變量有關，則結構功能函數即為

Z=g(R，S)=R-S

(1)

當R、S均服從正態分布，且相互獨立時，則結構的失效概率為

(2)

失效概率為

(3)

其中，z0表示結構的極限功能，如強度、撓度、裂縫極限寬度等極限狀態。

(一)對數正態分布統計理論

在疲勞理論中，常用的對數正態分布分布形式為Y=lg(X)，其對數正態分布分為

基本變量X的概率密度函數為

(4)

對數正態分布的累積分布函數為

(5)

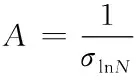
則Y1=AX-C

(6)

(二)Weibull分布統計理論

在某一特定循環荷載作用下，混凝土疲勞壽命N服從一定的分布規律，用Weibull函數可表示為

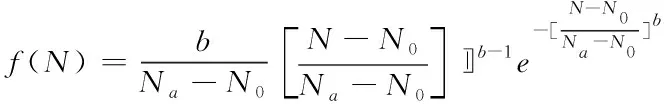
(7)

其中，N0—最小壽命參數；Na—特征壽命參數，36.8%存活率下的安全壽命；b—Weibull形狀參數。

可得

(8)

可得:Y=bX-α

(9)

式(9)即為可檢驗試驗數據是否符合兩參數的Weibull分布判斷標準。若試驗數據線性回歸表明Y與X之間線性關系良好，則說明數據符合兩參數威布爾分布。

二、混凝土疲勞壽命的概率分析

以文獻[13]中的試驗數據為例，利用上文推導結果對混凝土疲勞壽命進行概率分析結果并以Xi=lnNi為橫坐標，Y=φ-1(F(lnNi))為縱坐標，則其線性回歸檢驗結果分別如圖1中各分圖所示。

(a1)Smax=0.85

圖1 混凝土疲勞壽命的對數正態分布線性回歸檢驗

三、結果分析

由圖1的對數正態分布線性回歸結果可知，函數Y=φ-1(F(lnNi))和Xi=lnNi在各應力水平下均存在良好的線性關系。并在失效概率p=50%的條件下，按文獻[14]等所給出的疲勞壽命N的方程形式。

lgS=lg0.89443-0.0431lgN，

(10)

同樣，由圖2也可以看出，變量和變量Xi=lnNi在各應力水平下存在良好的線性關系，并在失效概率p=50%的條件下，其疲勞方程為：

lgS=lg1.0998-0.0436lgN，

(11)

由以上分析可知，混凝土疲勞壽命既服從雙對數正態分布，又服從雙對數的雙參數Weibull分布。但對于較低應力水平條件下，混凝土疲勞壽命數據離散性較小；而在應力水平較高時，混凝土疲勞壽命數據離散性則較大；反映在不同回歸結果分析中，則Weibull分布更敏感于對數正態分布，即離散性越小，則Weibull分布回歸系數越大；離散性越大，則Weibull分布回歸系數越小。這說明，Weibull分布能夠同步反映混凝土疲勞壽命數據的可靠性，因此也更加適合對混凝土疲勞壽命分析。另一方面，在較高的應力水平下，混凝土疲勞壽命數據離散性大，反映在試驗中，則需要盡力避免干擾因素，如提高配合比設計水平，提高試件成型與養護工藝，試驗步驟嚴格遵照相關規范和規定執行等技術保障措施，努力提高試驗精度；而反映在工程評估中，則需要給出較保守的評價才較為可靠。

四、結論

對數正態分布和雙參數Weibull分布都可以用來描述混凝土疲勞壽命S-N方程，但后者更敏感于前者對離散數據的變化。其中，具體地用上述兩種分析方法的相關系數進行評價時發現，當應力水平較高時，混凝土疲勞壽命數據離散性較大；而當應力水平較低時，混凝土疲勞壽命數據離散性則較小。因此，對于較高應力水平時，在試驗過程中，應努力提高試驗精度；而在工程評估中，則需偏于保守評價，否則易突發結構安全隱患。