鐵路客運樞紐公交車調度研究

(重慶交通大學交通運輸學院 重慶 400074)

一、引言

公交作為我國城市交通系統的重要組成部分，我國鐵路客運樞紐站中的公交車調度問題基本上還停留在傳統的人工調度層面，對鐵路樞紐站中公交車的換乘調度并沒有一個有效的優化模型。樞紐站內公交與其他主流交通方式之間不能得到有效的銜接，乘客換乘等待時間過長，樞紐站內部乘客滯留形成擁堵。

二、問題描述

我國鐵路建設時間與經驗的不足，樞紐內部的各種交通方式之間的轉換銜接存在不匹配的情況，乘客不能及時的實現換乘，導致樞紐站內部乘客滯留，產生擁堵現象，各種交通方式之間不能很好的銜接，國內對于鐵路客運樞紐中公交車的協調研究大部分集中于運能協調與換乘時間協調方面，以樞紐站系統成本最少為先提條件，乘客換乘總費用最少為目標建立模型求解出最優發車數與發車時間間隔。

三、調度模型的建立

鐵路運行線路與時間基本是固定不變的，可變性很小，要想通過協調鐵路的運行時間來實現公交的換乘極其困難；公交車的出發與到站時間受人為影響因素很大，運行時間的可變性較大，對公交車的運行進行調度來實現其他交通方式與公交車的銜接轉換也較為容易。

考慮到公交公司的利益與乘客出行等待可接受性等方面，公交車的調度問題主要包含兩個方面：發車數量，對于公交車公司來說，車輛數量的控制直接影響到成本的大小，要盡可能的使用最小的車輛達到最大的運載量，所以，對于公交公司來說控制公交車的發車數量尤為重要；發車間隔，乘客出行總是希望等待時間最小，最好是能夠達到隨到隨走程度，處于前面說過的車輛控制的前提下，通過調整公交車的發車間隔時間來實現。

(一)運能協調

本文僅討論站前廣場的始發(終點)線路和途徑線路停靠站兩種情況。

(1)

N1始發站公交車線路數；P公交車輛額定載客人數；β換算成標準車換算系數；rm1始發線路公交車的理論極限滿載率；ta1始發站公交車平均發車間隔

(2)

N2途經站公交車線路數；rm2途徑站公交車理論極限滿載率；ra途徑站公交車理論平均滿載率；ta2途徑站公交車平均發車間隔

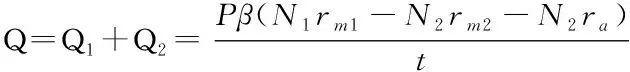
(3)

nb3——途徑站公交車理論平均滿載率

假設鐵路樞紐的高峰小時到站客流換乘公交車的流量為Qmax，對比計算出的Q與換乘流量的大小：

若Q≥Qmax，表示現有的公交線路滿足需求，不需要增加新的線路；

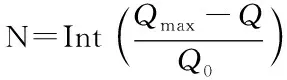
(4)

N新增加的公交線路數；Q0新增加的每輛公交車在高峰小時能夠提供的接運能力

若計算得出的N≥1，則將結果取整得出需要增加的線路數；

若計算得出的N=0，則不需要增加新的線路，只需要通過調整現有的線路數來協調即可。

(二)時間協調

在鐵路樞紐站中，換乘時間分為兩部分：一部分為鐵路樞紐站周邊區域步行到公交車站候車的乘客的步行時間，另外一部分為從鐵路樞紐站內部由其他交通方式(這里主要是鐵路運輸方式)換乘公交車的乘客的換乘時間。

1.樞紐站周圍區域步行到公交站的總候車時間成本M2為：

(5)

Qm1步行到公交車站的乘客流量；α乘客到達率；tr公交車發車間隔時間；φ乘客出行的時間價值

2.在一定的時間段[t1,t2]內，在鐵路樞紐站內部由其他交通方式(主要為鐵路)到達樞紐站并換乘公交車的總換乘時間成本M2為：

(6)

Qm2在一定時間內從第j次列車到達后換乘公交站的換乘流量；t0在一定時間內第1次公交車的發車時間；ti在一定時間內第i次公交車的發車時間(ti=t0+i·tr)；tj在一定時間內第j次列車的到達時間；tw乘客換乘公交車時從鐵路站臺到達公交站臺的時間(包括出站檢票和步行等時間)

此模型是以乘客的換乘時間總和最小為條件的函數模型，在乘客到達公交車站點客流特性不同的時間段[t1,t2]內，換乘時間成本的協調模型M=M1+M2，即目標函數為：

(7)

滿足換乘時間成本總和M最小條件的情況下，求出最小發車間隔時間tr，其中，還需要滿足以下約束條件：

t1≤ti≤t2(i=1,2,…n)t1≤tj≤t2(j=1,2,…m)

tmin≤tr≤tmax(tmin、tmax分別為根據正常情況下的鐵路運輸樞紐站客流研究出的能夠滿足相應的服務水平的公交車最小、大發車時間間隔，本文tmin=15min,tmax=30min)

四、結語

公交車是鐵路樞紐運輸系統的重要組成部分，對公交車的調度建立優化模型，可以根據計算出需要的公交車輛數和各時段最優的發車時間間隔，有效的節省公交車公司的成本，也能減少樞紐站中換乘公交車的等待時間，使客流由于等待車輛而滯留樞紐站的情況得到改善，有利于減少樞紐站擁堵情況，有利于完善城市交通系統，對居民的出行狀況改善、城市擁堵的治理具有積極意義。