基于漸進損傷的纖維全纏繞鋁內膽氣瓶自緊工藝

章 昕 趙建平

(南京工業大學機械與動力工程學院，南京 211816)

0 引言

復合材料壓力容器在工業生產中有著重要的應用，它綜合了傳統壓力容器和復合材料的優勢，大大提升了壓力容器的使用范圍、效率和壽命[1]。國內外對于復合材料壓力容器失效的分析和性能的預測主要方法為有限元軟件分析與試驗結果相對照，來驗證分析結果的可靠性。纖維纏繞復合材料壓力容器，由于其復合材料層的纖維纏繞結構的特殊性，在承載的過程中其應力是漸進變化的，材料性能也是逐漸退化的，因此需要運用漸進損傷的分析方法對復合材料層進行分析[2]。在諸多的復合材料壓力容器中，復合材料氣瓶使用最為廣泛。纖維纏繞氣瓶又因其封頭處纏繞方法的特殊性，要利用經典網格理論對氣瓶封頭處的幾何方程進行分析[3]。

通常在氣瓶水壓試驗之前，需要進行一次自緊工藝循環，自緊力的大小往往高于水壓試驗壓力，使得氣瓶承載自緊力時內襯層發生屈服，自緊力卸載后內襯層存在一定的殘余壓應力，氣瓶再承載時抵消一部分應力，提高氣瓶承載力和疲勞壽命，同時優化內襯層和復合材料層之間的應力分布[4-5]。

自緊工藝對氣瓶是必不可少的一道工藝，本文基于復合材料的漸進損傷的分析方法，從理論和數值模擬的角度分析了復合材料氣瓶自緊工藝的原理以及必要性，確定了合理自緊力的范圍。

1 復合材料的漸進失效分析

1.1 復合材料失效準則和材料退化模式

復合材料的失效準則依據不同的分類標準可以分為很多類。依據在失效分析過程中有無失效模式可以分為：模式相關準則和模式無關準則。最大應力準則、最大應變準則、蔡-希爾(Tasi-Hill)強度準則、蔡-吳(Tasi-Wu)張量強度準則均屬于模式無關的失效準則[2]。

三維Hashin失效準則屬于模式相關的失效準則。具體內容為[6-8]：

(1)纖維拉伸失效(σ11>0)：

(1)

(2)纖維壓縮失效(σ11<0)：

(2)

(3)基體拉伸失效(σ22>0)：

(3)

(4)基體壓縮失效(σ22<0)：

(4)

(5)基體拉伸剪切失效(σ11<0)：

(5)

(6)拉伸分層失效(σ33>0)：

(6)

(7)壓縮分層失效(σ33<0)：

(7)

式中,7個失效判據σ11，σ22，σ33，τ12，τ13，τ23分別表示單層板中的6個應力分量；XT，XC，YT，YC，S12，S13，S23，ZT，ZC分別表示單層板材料性能的9個常數。

復合材料層局部放大可以看作是層合板結構[2]。層合板結構在承載的過程中，某一單層板發生損傷時，層合板不會直接失去承載能力，而是通過剛度矩陣的折減來實現材料性能退化的過程[9]?；贑hang和Camanho材料剛度折減方案，提出剛度折減方案，具體內容見表1。其中，當折減系數為1時表示該材料參數沒有發生折減。

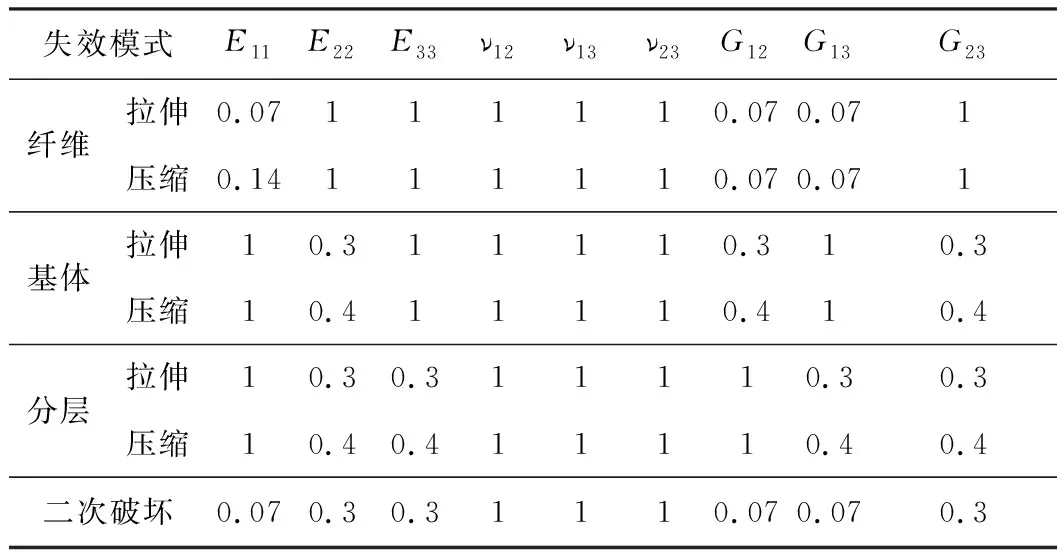
表1 材料性能參數退化表

1.2 VUMAT子程序編寫及驗證

參照復合材料漸進損傷分析的理論過程，主要包括應力應變的計算、失效模式的判斷、失效評定、載荷的增加、剛度折減和最終失效等內容。邏輯圖如圖1所示。

根據文獻[10]，選用如圖2所示的層合板模型來驗證子程序的正確性。層合板結構中間開孔，開孔直徑D=15 mm，長度L=250 mm，寬度W=25 mm，厚度t=1.68 mm。層合板左端面施加全約束，層合板右側施加位移約束。

模型計算可得，層合板的失效載荷為1.14 kN，在該力的作用下層合板沿纖維方向的應力S11的值為310.4 MPa，而文獻中試驗所得的數據為290.0 MPa，兩者誤差為7.03%，說明子程序的正確性。

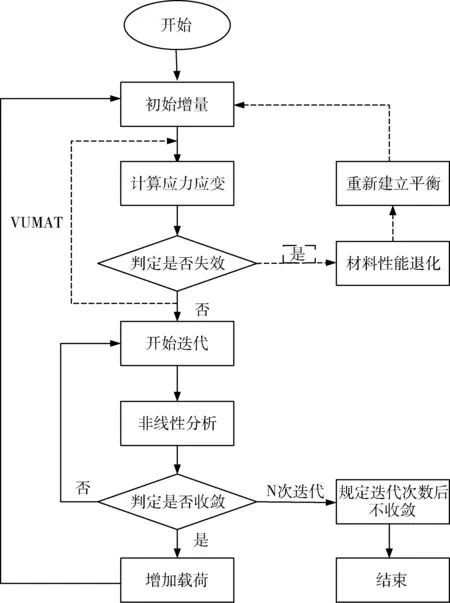
圖1 子程序編寫邏輯圖Fig.1 Logic diagram of the VUMAT program

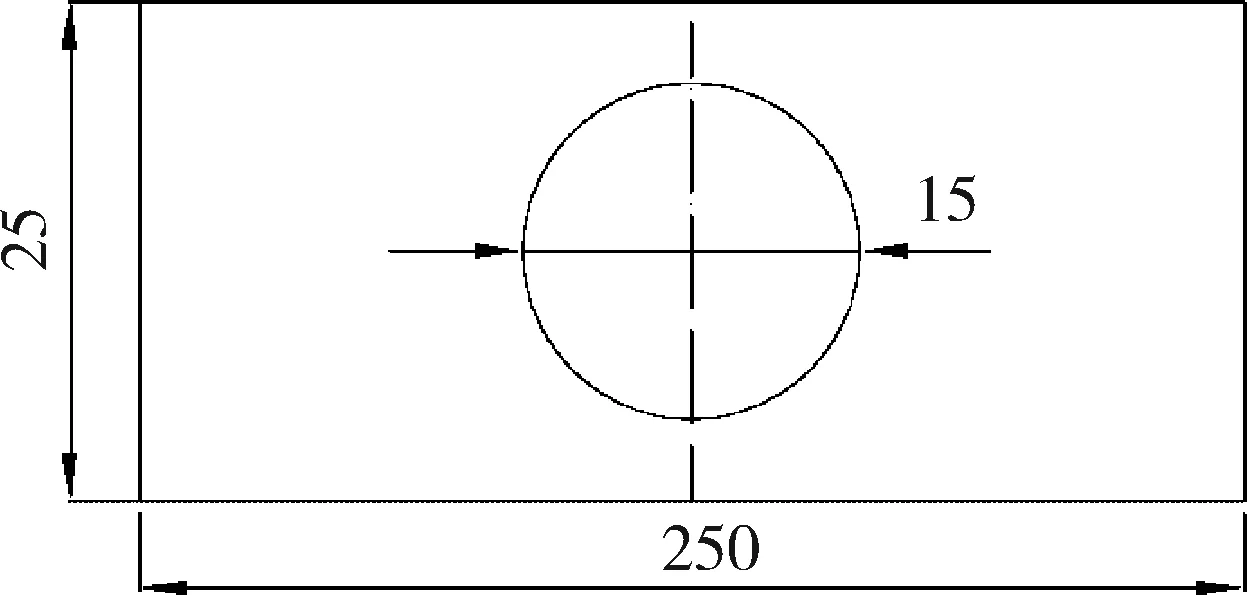
圖2 含開孔結構復合材料層合板Fig.2 Composite laminated plates with a center hole curve of layup under tensile loads hole

2 氣瓶的漸進損傷分析

2.1 氣瓶的幾何模型

本文分析的對象為纖維全纏繞鋁內襯氣瓶，采用ABAQUS有限元軟件建立模型并運用VUMAT子程序分析計算。氣瓶內襯的內徑為95 mm，壁厚為2.5 mm，筒身段的纏繞方式為環向和螺旋纏繞組合的方式，纏繞順序為[90°2/14°2/90°2/14°2/90°2/14°2]，其中，環向纏繞層的纖維厚度為0.16 mm，螺旋纏繞層的纖維厚度為0.18 mm，封頭段只存在螺旋纏繞。封頭段纖維纏繞厚度是隨著平行圓直徑的變化而變化，按照式(8)(9)進行計算[11]，計算結果見表2。由于

氣瓶結構的對稱性和受力的對稱性，建立實際結構環向的1/2模型進行分析和計算。

α=arcsin (r/R)

(8)

(9)

式中,α為纖維纏繞角；r為極孔半徑；R為纖維纏繞處平行圓半徑；R0為內襯筒身段半徑；tf為纏繞層厚度。

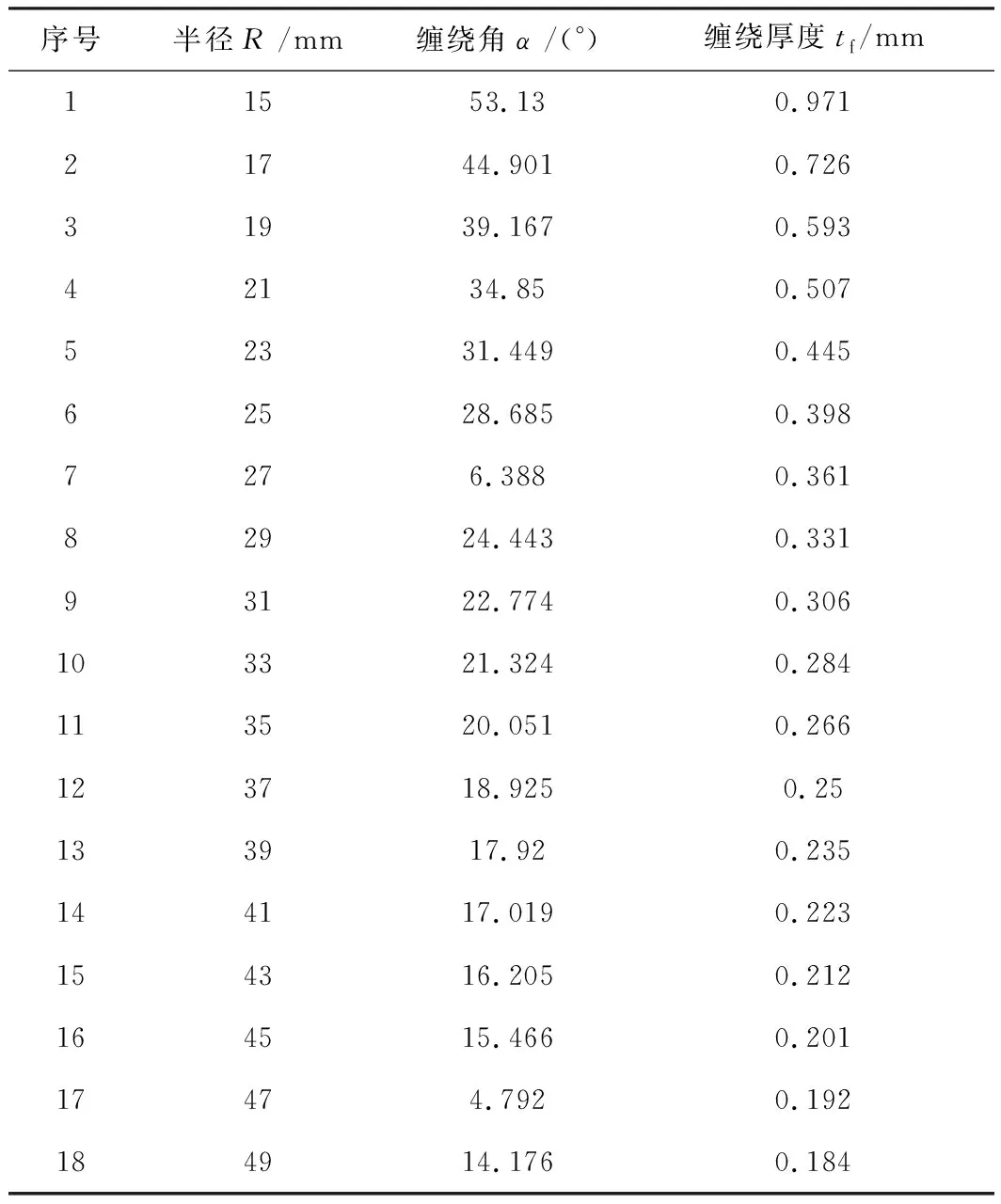
表2 封頭纖維纏繞角和纖維纏繞厚度隨平行圓半徑變化Tab.2 Wound angle and real thickness of the composite on the head according to the radius of the parallel circle

氣瓶內襯材料為鋁合金6061Al-T6，材料性能參數見表3。纖維纏繞層采用T700型碳纖維為增強材料，環氧樹脂為基體材料，材料參數見表4。依據對稱性，在軸向對稱面施加對稱約束，在內襯層和纖維纏繞層之間施加綁定約束。

表3 鋁合金6061Al-T6力學性能[12]

表4 復合材料T-700/環氧樹脂力學性能[13]

2.2 復合材料漸進損傷分析

從16 MPa開始逐漸增加氣瓶內壓直至爆破，探究氣瓶的應力變化和復合材料的損傷累積和發展的過程。

2.2.1復合材料層損傷過程

(1)基體拉伸損傷，圖3為基體拉伸損傷的發展過程，如圖所示基體拉伸損傷發生較早，內壓為25 MPa時萌發，由封頭開始向筒體發展。螺旋纏繞層最先發生，由復合材料層外側向內側發展。內壓為34 MPa時，筒體開始大面積出現失效單元，40 MPa時，發展更加迅速。

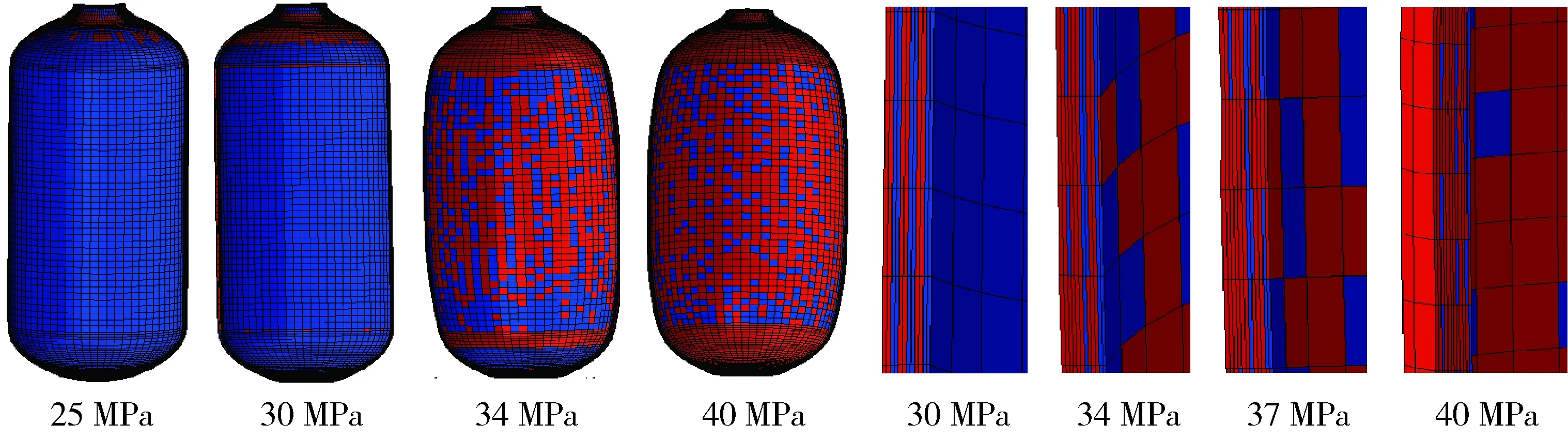
圖3 復合材料層基體拉伸損傷隨內壓的發展Fig.3 Development of matrix tensile damage of composite under increasing internal pressure

(2)基體壓縮失效，圖4為基體壓縮損傷的發展過程，基體壓縮損傷從內壓為34 MPa開始，由筒體中部開始向兩端發展，螺旋纏繞層最先發生，由復合材料層內側向外側發展。

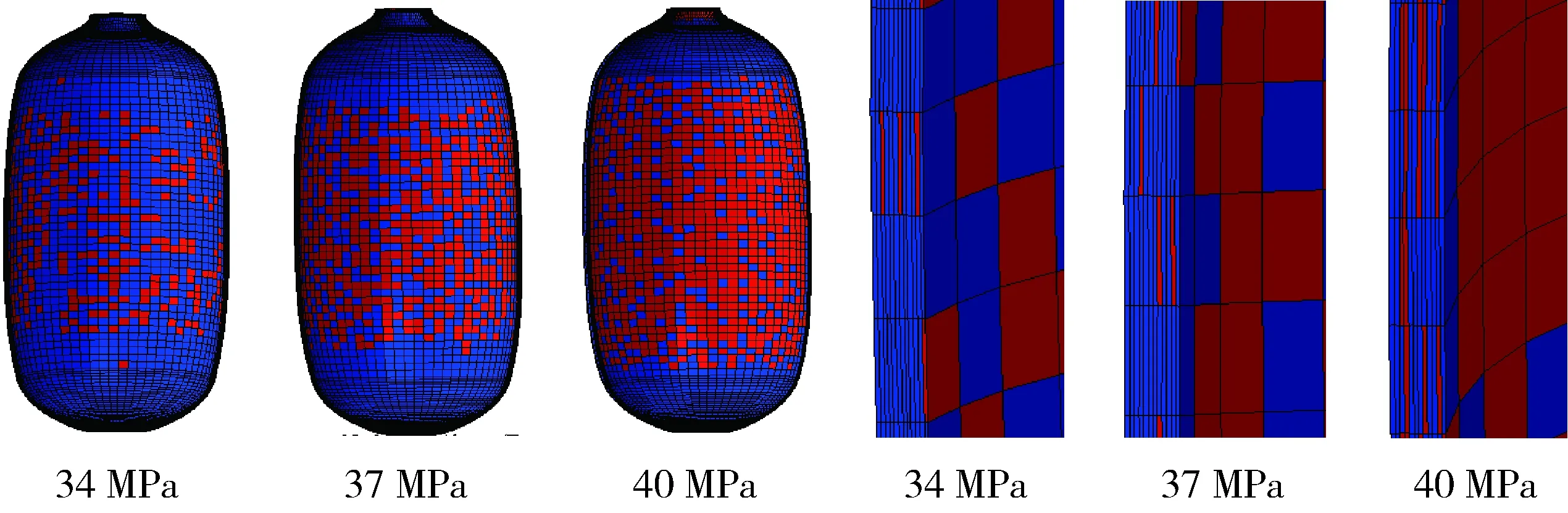
圖4 復合材料層基體壓縮損傷隨內壓的發展Fig. 4 Development of matrix compression damage of composite under increasing internal pressure

(3)拉伸分層失效，圖5為拉伸分層損傷的發展過程，拉伸分層損傷從內壓為30 MPa開始，由筒體底部開始向頂端發展，由復合材料內側向外側發展。

圖5 復合材料層拉伸分層損傷隨內壓的發展Fig.5 Development of tensile delamination damage of composite under increasing internal pressure

(4)纖維拉伸失效，圖6為纖維拉伸損傷的發展過程，纖維拉伸損傷從內壓為34 MPa開始，由筒體中部向兩端發展，由內側向外側發展，當內壓為40 MPa時開始向封頭發展。

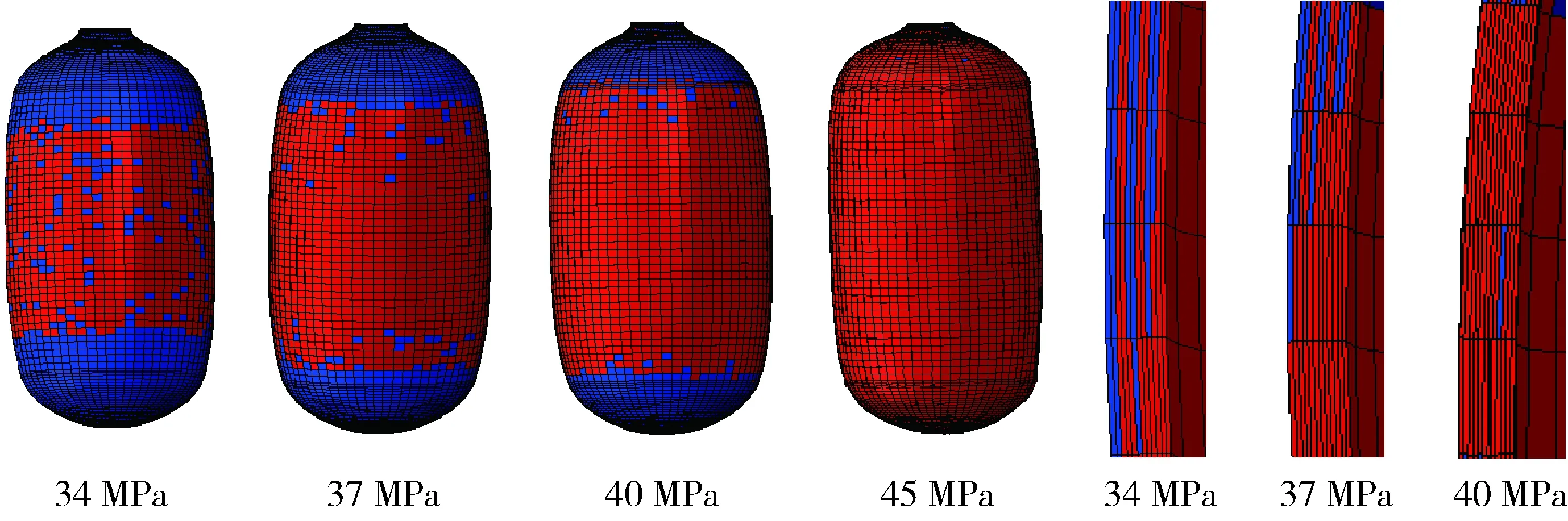
圖6 復合材料層纖維拉伸損傷隨內壓的發展Fig.6 Development of fiber tensile damage of composite under increasing internal pressure

綜上，復合材料層損傷發生的順序或可能性：基體拉伸>拉伸分層>纖維拉伸/基體壓縮。且損傷大都從螺旋纏繞層開始。除基體拉伸損傷由封頭向筒體發展，由復合材料外層向內層發展，其余損傷大都從筒體中部向兩端發展，由內層向外層發展。對于算例模型，當內壓達到34 MPa時，筒體開始出現多種模式的損傷，因此從減少復合材料損傷的角度，自緊力應小于34 MPa。

2.2.2氣瓶的應力分析

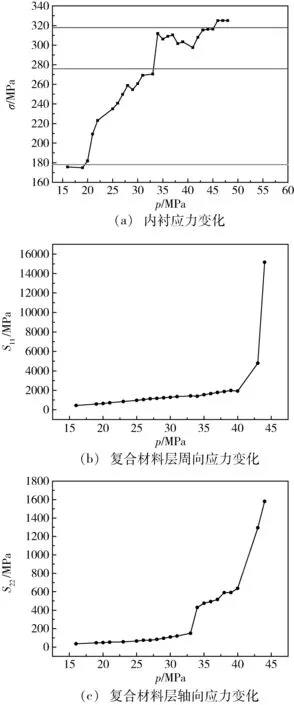
圖7 復合材料氣瓶應力隨內壓的變化Fig.7 Stress of composite cylinder under increasing internal pressure

氣瓶內襯應力變化和復合材料層周向及軸向應力變化見圖7。由圖7(a)可知，內襯應力隨內壓的增加逐漸變大，內壓為34 MPa時內襯應力開始大幅增加，在44 MPa時應力達到拉伸強度318 MPa。由圖7(b)可知，當內壓達到40 MPa時，復合材料層周向應力大幅增加，到44 MPa時應力激增，說明44 MPa為爆破壓力。由圖7(c)可知，內壓分別在34和40 MPa時，復合材料層軸向應力大幅增大。因此從應力變化的穩定性角度，自緊力應小于34 MPa。

由DOT—CFFC 2007標準[14]可知，工作壓力下的復合材料氣瓶的內襯上任一點的最大拉伸應力不得超過材料屈服強度的60%，即276×60%=178 MPa，由圖7(a)可知，氣瓶的最大工作壓力為20 MPa。假設筒身達到爆破壓力pb，且認為殼體爆破時縱向和環向纖維抗力都達到發揮強度即Xt、Yt，則纖維環向總厚度為[15]：

(10)

式中，R為筒體半徑，pb為爆破壓力，α為螺旋層角度，tfθ為環向層總厚度。

將爆破壓力為44 MPa代入式(10)，可得纖維環向層總厚度為1.1 mm，與實際環向層總厚度0.96 mm，誤差為14.5%，在工程允許的誤差范圍內，說明了有限元結果的正確性。

3 氣瓶的自緊工藝

在氣瓶水壓試驗之前，進行一次自緊工藝，自緊力的大小往往高于水壓試驗壓力，使得自緊時內襯層發生屈服，自緊力卸載后內襯層存在一定的殘余壓應力，氣瓶再承載時可抵消一部分應力，優化內襯層和復合材料層之間的應力分布。ASME規定，水壓試驗壓力：

pT=1.3pw(σ/σt)

(11)

式中，pT為水壓試驗壓力，pw為最大允許工作壓力，(σ/σt)為應力修正系數。

應力修正系數取1，由氣瓶的應力分析可知pw為20 MPa，所以pT為26 MPa。因此自緊力取值應大于26 MPa，結合復合材料漸進損傷分析，自緊力應小于34 MPa。分別取工作壓力為20、25 MPa，取自緊力范圍為28～39 MPa進行試算，氣瓶的應力變化見圖8～圖10。特別的，圖中橫線表示25、20 MPa工作壓力下未經自緊工藝處理的氣瓶的應力水平。

由圖8可知，隨著自緊力的增加，工作壓力下氣瓶內襯的應力先減小后增大。當自緊力為30～33 MPa時，內襯應力低于未經自緊的氣瓶內襯的應力，當自緊力為30 MPa時，內襯應力達到最低，即自緊水平最好。

由圖9和10可知，當自緊力為30～33 MPa時，經過自緊工藝的氣瓶的復合材料層的周向及軸向應力遠大于未經自緊的氣瓶的復合材料層的周向及軸向應力，說明自緊工藝改善了氣瓶結構的應力分配。

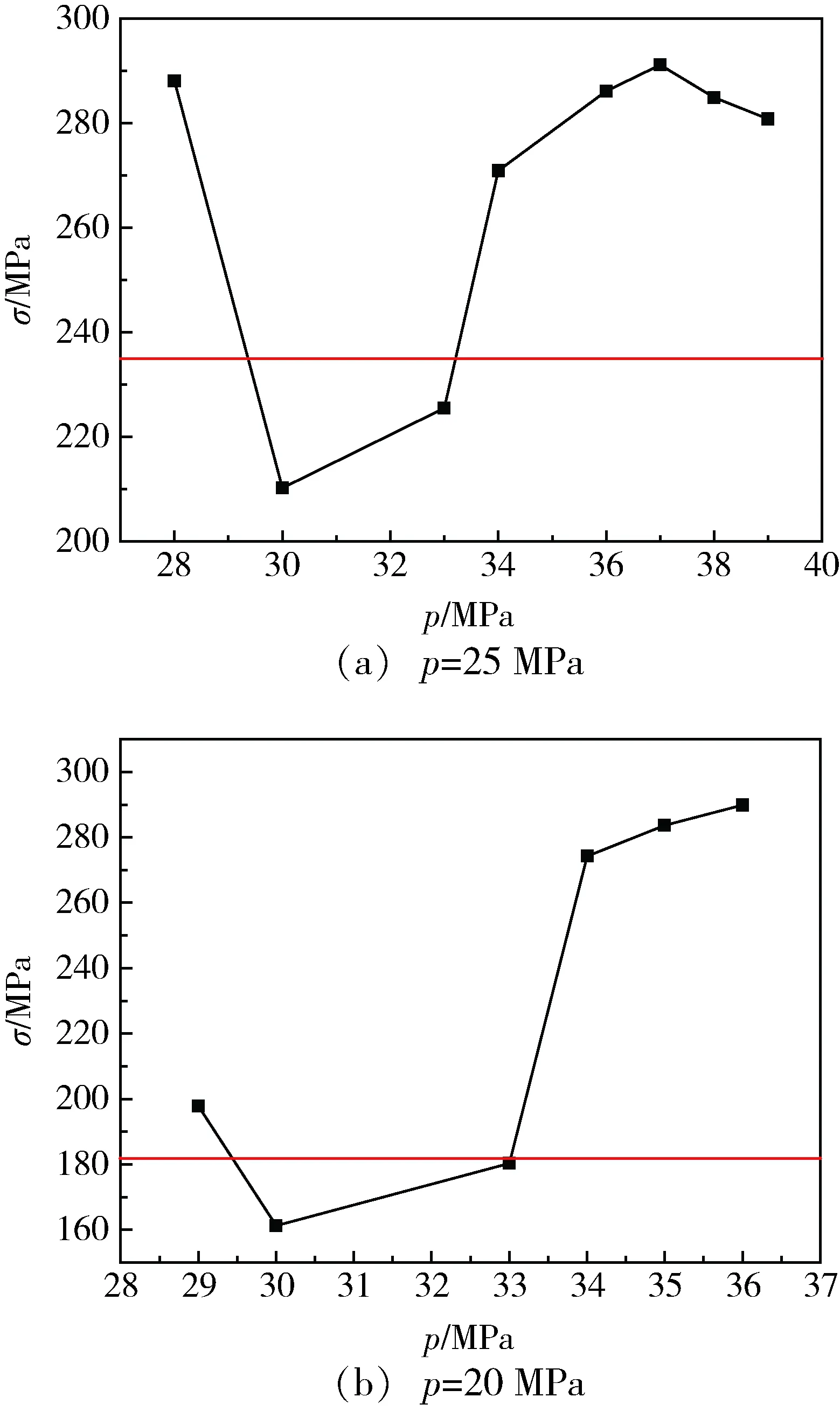
圖8 不同自緊力下，內襯應力的變化Fig.8 Stress of liner under different force of autofrettage

圖9 不同自緊力下，復合材料層周向應力的變化Fig.9 Circumferential stress of composite layer under different force of autofrettage

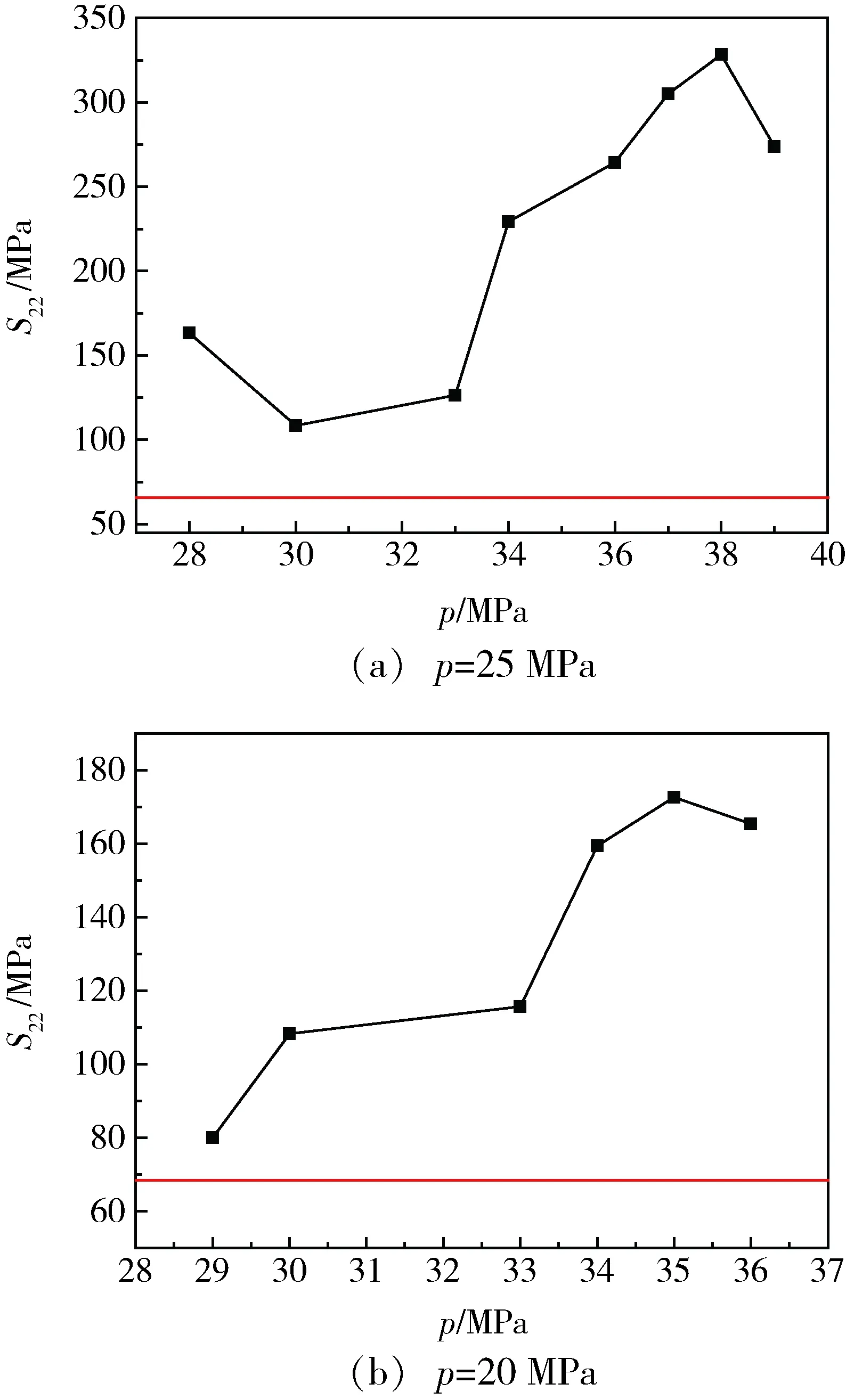
圖10 不同自緊力下，復合材料層軸向應力的變化Fig.10 Axial stress of composite layer under different force of autofrettage

根據DOT-CFFC 2007[14]，自緊力下內襯的筒身段必須處于屈服狀態，自緊力卸載后內襯層Mises最大應力應大于內襯材料屈服強度的60%，但不得超過其屈服強度的95%。圖11是不同自緊力作用下，氣瓶卸載后內襯的應力?？芍斪跃o力為30～33 MPa時，卸載后的氣瓶內襯壓應力大于屈服強度60%，即177.6 MPa，小于屈服強度95%，即262.2 MPa，滿足規定要求。

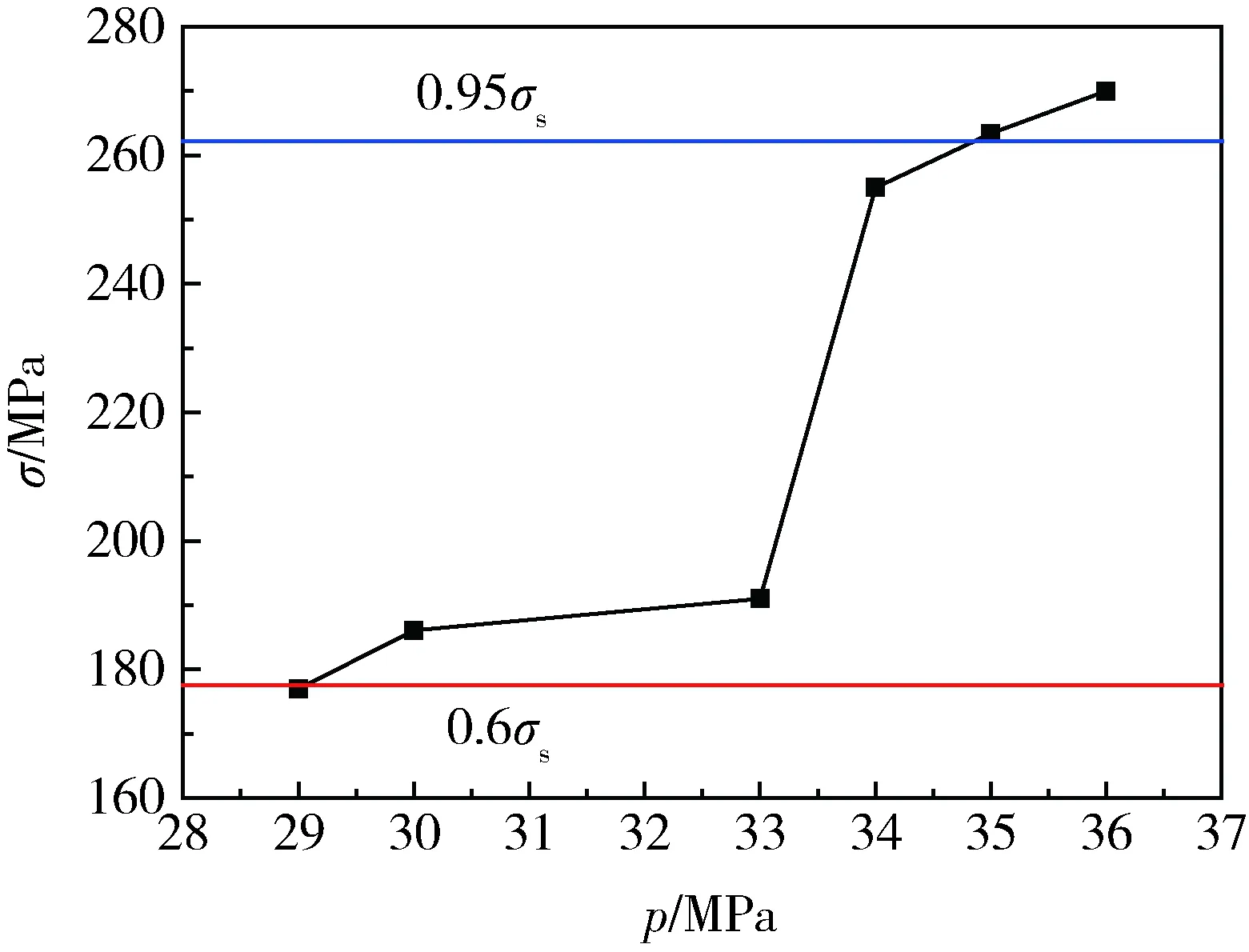
圖11 不同自緊力作用，卸載后內襯的應力Fig.11 Stress of liner under load-off after different force of autofrettage

等效塑性應變圖描述的是整個過程中結構塑性應變的累積結果[2]。圖12是沿路徑從極孔頂端到氣瓶底部的等效塑性應變的分布情況，可知，30 MPa的自緊力作用時，氣瓶筒身段不僅處于屈服狀態，且等效塑性應變最大，滿足規定要求。

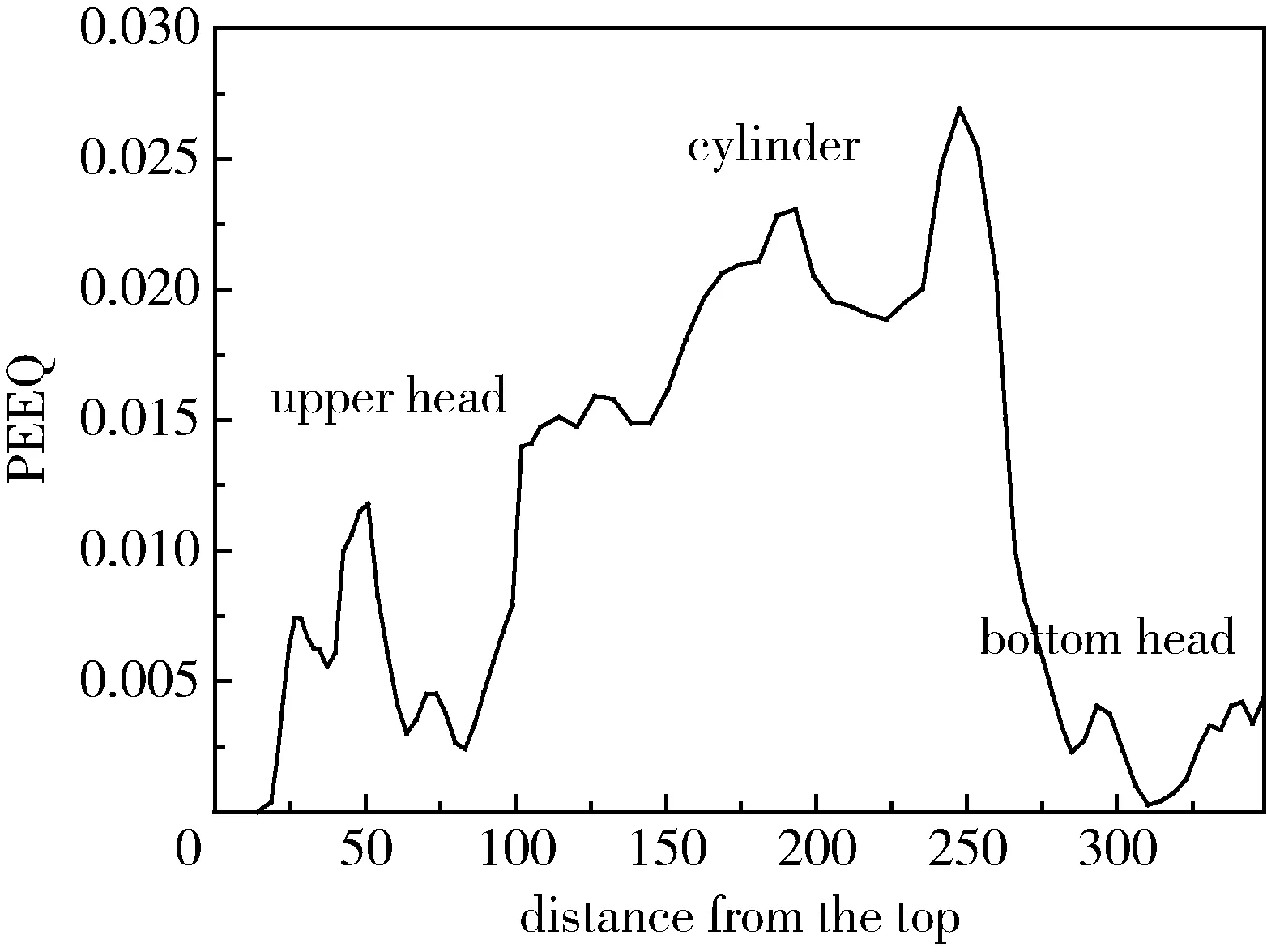
圖12 30 MPa自緊力作用時，氣瓶的塑性等效應變Fig.12 Plastic equivalent strain of cylinder under 30 MPa force of autofrettage

綜上，當自緊力為30～33 MPa，即最大工作壓力的1.5～1.65倍時，氣瓶內襯應力減小，復合材料層應力大幅提高，氣瓶應力分配得到改善承載能力得到提高，是合理的自緊力范圍。從減少復合材料的損傷和最大程度降低內襯應力的角度，最優自緊力應為30 MPa，即最大工作壓力的1.5倍。

4 結論

本文基于漸進損傷分析的方法，從數值模擬角度分析了氣瓶復合材料層漸進損傷發展和累積的過程以及氣瓶的應力變化。驗證了自緊工藝對提高氣瓶承載能力的必要性，確定了合理自緊力的范圍，結論如下。

(1)基于復合材料漸進失效分析，全纏繞氣瓶復合材料層損傷發生的順序或可能性：基體拉伸>拉伸分層>纖維拉伸/基體壓縮，且損傷大都從螺旋纏繞層開始。除基體拉伸失效由封頭向筒體發展，由復合材料外層向內層發展，其余損傷大都從筒體中部向兩端發展，由內層向外層發展。對于算例模型，當內壓達到34 MPa時，筒體開始出現多種模式的損傷，因此從減少復合材料損傷的角度，自緊力應小于34 MPa。

(2)基于氣瓶的應力分析，當算例模型內壓為34 MPa時內襯應力開始大幅增加，在46 MPa時應力達到拉伸強度。當內壓達到40 MPa時，復合材料層周向應力大幅增加，到44 MPa時應力激增。內壓分別在34和40 MPa時，復合材料層軸向應力大幅增大。因此從應力變化的穩定性角度考慮，自緊力應小于34 MPa。

(3)基于氣瓶的自緊工藝的研究，當自緊力為最大工作壓力的1.5～1.65倍時，氣瓶內襯應力減小，復合材料層應力大幅提高，氣瓶的應力分配得到改善，是合理的自緊力范圍。從減少復合材料的損傷和最大程度降低內襯應力的角度，最優自緊力應最大工作壓力的1.5倍。