基礎振動下插裝閥組抗振特性分析

楊忠炯，蔡岳林，周立強，李 俊

（1.中南大學 機電工程學院，長沙 410083；2.中南大學 高性能復雜制造國家重點實驗室，長沙 410083）

0 引言

插裝閥具有通流能力強、結構簡單、動作迅速、組件通用化、標準化程度較高等特點，因此工程實際中被廣泛應用。但不同通徑的插裝閥所允許通過的流量均有上限值，因此常常采用多個插裝閥并聯(lián)成一級的方式來滿足液壓系統(tǒng)大流量要求[1]。硬巖掘進機（簡稱TBM）所處的工作環(huán)境及工作要求，決定了其液壓系統(tǒng)所需工作壓力高、流量大。因此插裝閥組在TBM上廣泛采用。例如：遼寧大伙房水庫輸水工程建設中應用的羅賓斯公司MB264-311型TBM其液壓系統(tǒng)中大量采用插裝閥組[2]。TBM在硬巖掘進過程中會使機器產(chǎn)生強烈振動[3]。插裝閥組在TBM工作時，其工作性能會受到相應強振動的影響。因此需要對強振動環(huán)境下插裝閥組的抗振特性做一定深入的研究。

目前關于插裝閥的研究主要從單個閥體著手，并從內部結構方面進行研究，對插裝閥組的研究較少。鄭淑娟[4]通過計算流體力學方法對分析研究閥芯運動過程中的錐閥內流體運動狀態(tài)，研究得到了錐閥流量系數(shù)，瞬態(tài)液動力在閥芯啟閉過程中隨錐閥流量、開口度的變化曲線。賀小峰[5]提出一種利用U型消音槽來有效減小插裝閥在高壓大流量環(huán)境下工作所造成的振動與噪音，并建立相應插裝閥數(shù)學模型；王安麟[6]提出一種基于插裝閥組啟閉狀態(tài)的邏輯理論，來分析插裝閥組液壓系統(tǒng)瞬時失效機理，并提出一種通過增加閥組控制腔壓力的方法來提高液壓集成系統(tǒng)穩(wěn)定性。

上述各位學者的研究對于插裝閥及插裝閥組設計與控制具有重大意義，但均未考慮到插裝閥組在基礎振動下的工作特性。實際應用中的插裝閥組根據(jù)先導級數(shù)的不同，分為二級插裝閥組與三級插裝閥組；本文針對基礎振動對TBM插裝閥組性能的影響，仿真研究兩種插裝閥組的抗振特性，分析結果將為TBM插裝閥組的選型設計提供參考。

1 基礎振動下插裝閥組結構模型的建立

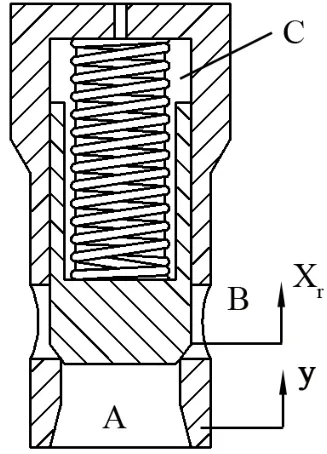
圖1 振動下插裝閥結構原理

從單個插裝閥結構入手建立基礎振動下插裝閥組結構模型，如圖1所示。假設插裝閥在簡諧運動y=Asinωt的基礎振動環(huán)境中工作，在該環(huán)境下，閥芯會受到振動慣性力作用。如上圖所示閥芯在進油口A、出油口B，控制腔C油壓力，及控制腔中彈簧力，閥芯振動慣性力等合力作用下開啟，此時閥芯相對于閥體的開啟高度為Xr。以下截取TBM主機液壓系統(tǒng)中的部分簡單的插裝閥組液壓回路，說明二級插裝閥組與三級插裝閥組于基礎振動下工作原理。

1.1 二級插裝閥組模型

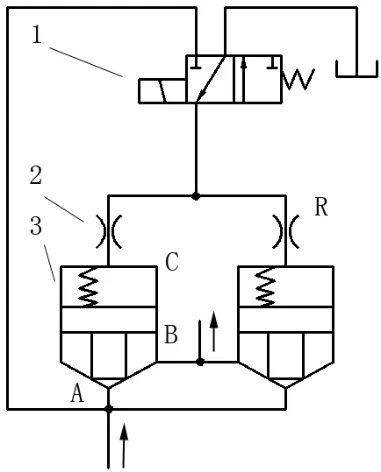
圖2 二級插裝閥組簡易工作油路

由圖2所示，該插裝閥組主閥3控制腔所連先導級為電磁閥1。在電磁閥斷電時，與進油口連通的控制油路通過電磁閥與插裝主閥控制腔相連，在控制腔與進出油口液壓合力作用下使閥關閉；在電磁閥通電后，此時與油箱相連的插裝閥控制腔C內油壓迅速減少，并且在系統(tǒng)合力作用下，主閥芯開啟。

1.2 三級插裝閥組模型

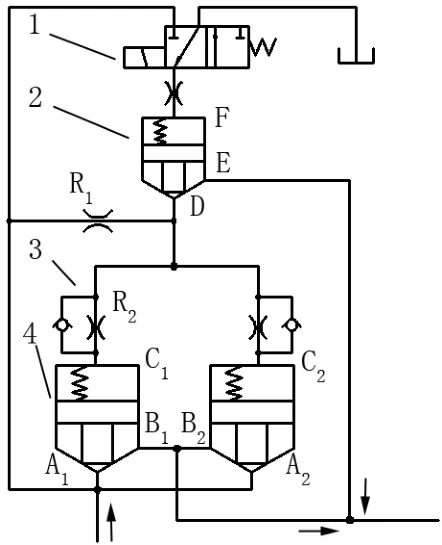
圖3 三級插裝閥組簡易工作油路

由圖3所示，該三級插裝閥組主閥A1、A2的控制腔與一通徑較小的插裝閥相連。電磁閥斷電后，進油口一側油路分為兩支，一支通過電磁閥與先導插裝閥2的控制腔相連，在壓力作用下使先導閥處于關閉狀態(tài)；另一油路通過阻尼孔R1與插裝閥D口相連，同時又通過單向節(jié)流閥與主閥4的控制腔相連。此時液壓油路各處的壓力相等，主閥處于關閉狀態(tài)。在電磁閥通電時，先導閥2控制腔F與油箱相連，油壓急劇下降，在系統(tǒng)油壓作用下，先導閥芯打開。并且油路通過阻尼孔R1后壓力下降，使控制腔C1、C2壓力急劇下降。由于先導閥2較大的過流面積，在進口的壓力油作用下，可以使控制腔C1、C2中的控制油液迅速排出推動主閥快速打開。

2 數(shù)學模型

二級插裝閥組在基礎振動下的數(shù)學模型較為簡單，不再列寫建立過程。根據(jù)以上基礎振動下插裝閥結構原理模型與三級插裝閥組簡易工作回路，通過建立基礎振動下三級插裝閥組的力平衡方程組與連續(xù)性方程組，建立其在基礎振動下的簡化數(shù)學模型，并作出以下假設：

1）視液壓系統(tǒng)工作介質為理想流體，流體參數(shù)均為常數(shù)；

2）工作介質壓力為常數(shù)，液壓系統(tǒng)各工作元件閥腔內壓力均勻分布；

3）忽略液壓元件內泄露對元件工作特性的影響；

4）忽略閥芯與閥套間的摩擦力及閥芯重量的影響；

5）忽略插裝閥組主閥間耦合作用，將主閥工作狀態(tài)視為等效一致。

基礎振動下，插裝閥運動機構將在進出口油壓力、液動力、彈簧力及基礎振動引起的慣性力合力下在縱向作受迫振動。基于強迫振動理論[9]，簡化插裝閥內部結構，建立如圖4所示彈簧-質量-阻尼模型。以插裝閥組其中一個主閥為對象，主閥閥芯與閥體的相對位移為Xr2，先導插裝閥閥芯與閥體的相對位移為Xr1；Pa1、Pb1、Pc1分別為主閥進油口A1腔，出油口B1腔，控制腔C1腔的壓力，Pd、Pe、Pf分別為二級先導插裝閥進油口D腔、出油口E腔、控制腔F腔的壓力，Aa、Ad、Ab、Ae、Ac、Af分別為液壓油路進油口A、D腔，出油口B、E腔，控制腔C、F腔的壓力作用面積。

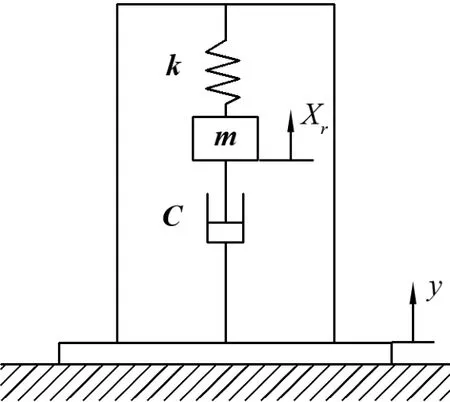
圖4 基礎振動下插裝閥閥芯運動物理模型

插裝閥組主閥芯基礎振動下運動微分方程為：

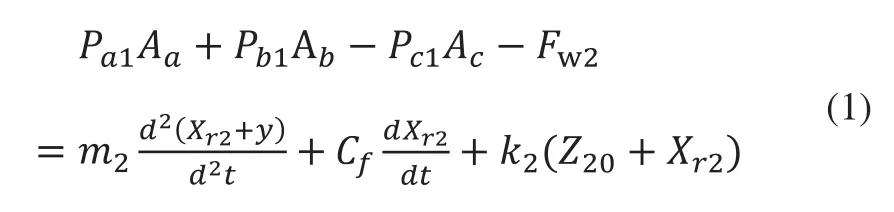
其中：m2為主閥閥芯質量；Cf為油液粘性阻尼系數(shù)；k2為主閥控制腔彈簧剛度；Z20為彈簧預壓縮量。

進油口流量方程為：

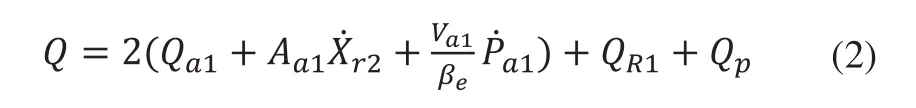
主閥閥口流量為：

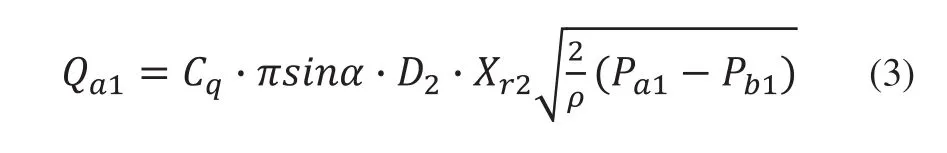
其中：Cq為閥口流量系數(shù)；D2為主閥閥座孔直徑，即α為閥口半錐角；ρ為液壓油密度。

先導電磁球閥口流量為：

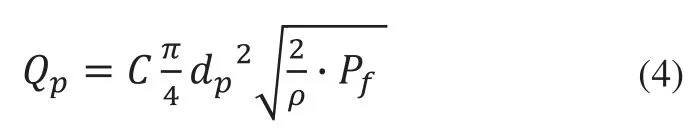
其中：C為流量系數(shù)，約為0.62～0.75；dp為先導電磁球閥過流孔徑。

主閥控制腔流量方程為：

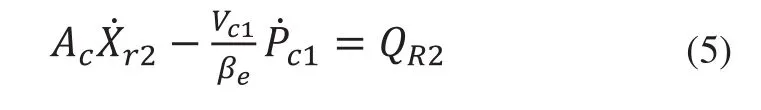
其中：Vc1為控制腔容積；βe為油液彈性模量；

二級先導插裝閥閥芯基礎振動下的運動微分方程為：

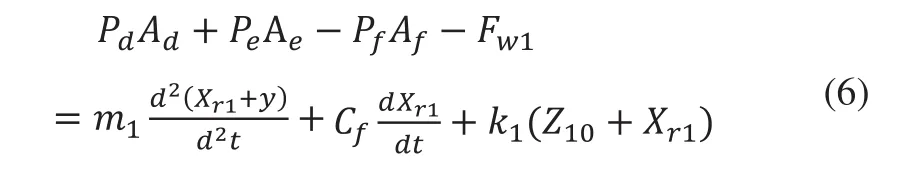
其中：m1為先導閥閥芯質量；k1為先導閥控制腔彈簧剛度；Z10為彈簧預壓縮量；

先導閥閥口流量方程為：

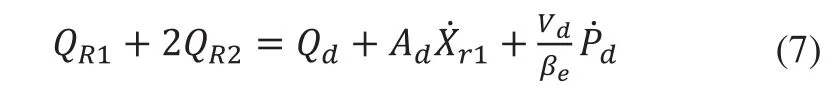
先導閥進出口流量為：

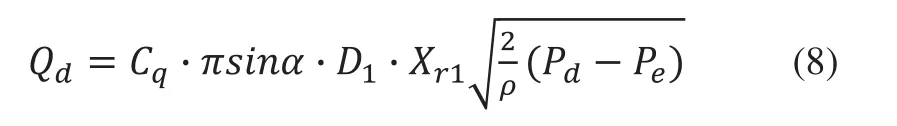
其中：D1為閥座孔直徑，即：

控制腔流量方程為：

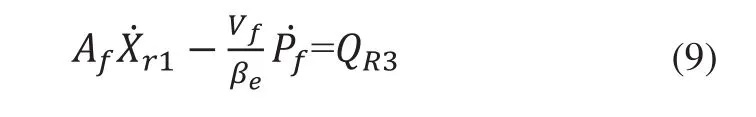
其中：QR3=Qp；Vf為先導閥控制腔容積。

液阻R1流量方程為：

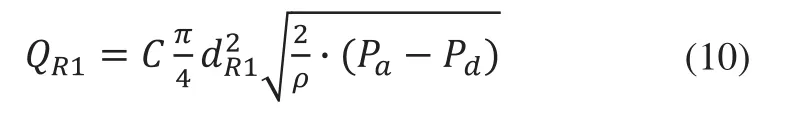
液阻R2流量方程為：

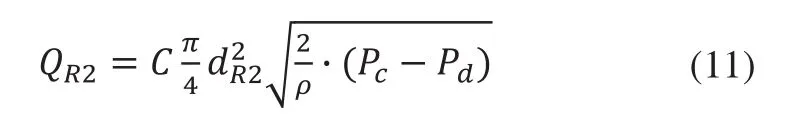
其中：dR1與dR2為阻尼孔過流孔徑。

插裝閥工作過程中還受到穩(wěn)態(tài)液動力作用，作用力方向總是使閥芯趨于關閉。其大小與閥口過流面積及閥口壓差有關，其方程為：

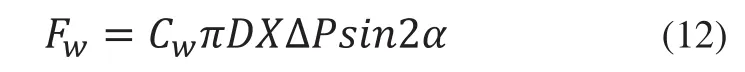
其中：Cw為穩(wěn)態(tài)液動力計算時閥口流量系數(shù)，約為0.77～0.82，X為閥芯開啟高度，?P為插裝閥進出口油液壓差，α為閥口半錐角；式(1)與式(6)中Fw2與Fw1為主閥與二級先導閥閥芯所受穩(wěn)態(tài)液動力。

3 仿真與分析

根據(jù)以上二級插裝閥組與三級插裝閥組結構模型與已建立的數(shù)學模型，建立相應液壓系統(tǒng)AMESim仿真模型。其液壓系統(tǒng)主要元件參數(shù)設置為：液壓泵排量為300ml/r，液壓泵轉速為2400r/min；設定安全閥開啟壓力為10MPa，其他系統(tǒng)技術參數(shù)如表1所示；插裝閥組主閥技術參數(shù)如表2所示，插裝閥組主閥芯最大工作行程為14mm，主閥控制腔液阻孔徑為1.2mm，彈簧剛度為50N/mm；二級先導插裝閥技術參數(shù)如表3所示；閥芯最大工作行程為7mm，控制腔液阻孔徑為0.8mm，彈簧剛度為10N/mm；

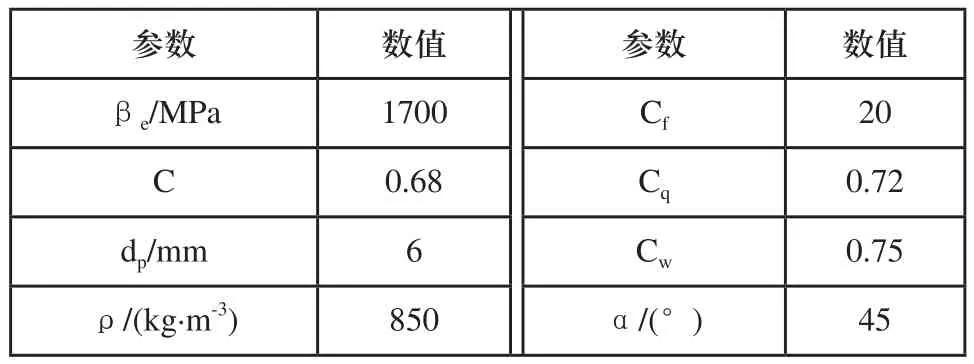
表1 仿真模型參數(shù)

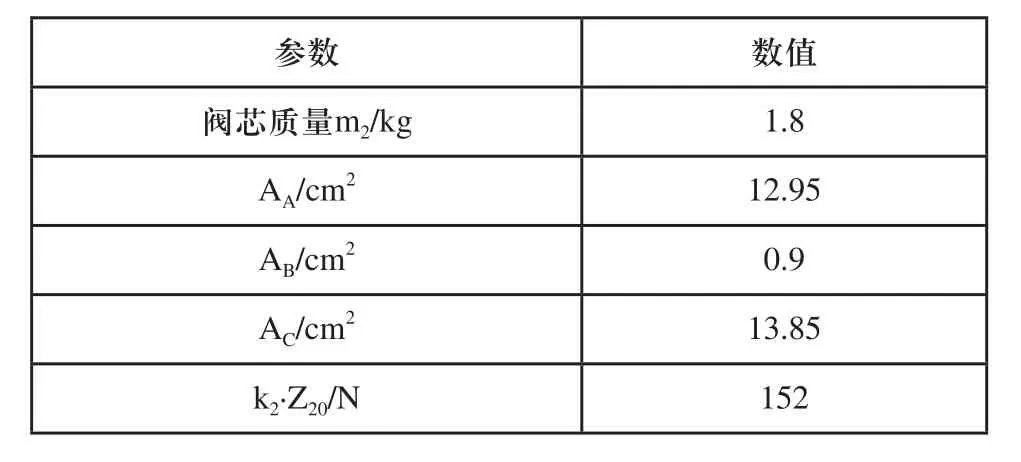
表2 插裝閥組主閥技術參數(shù)

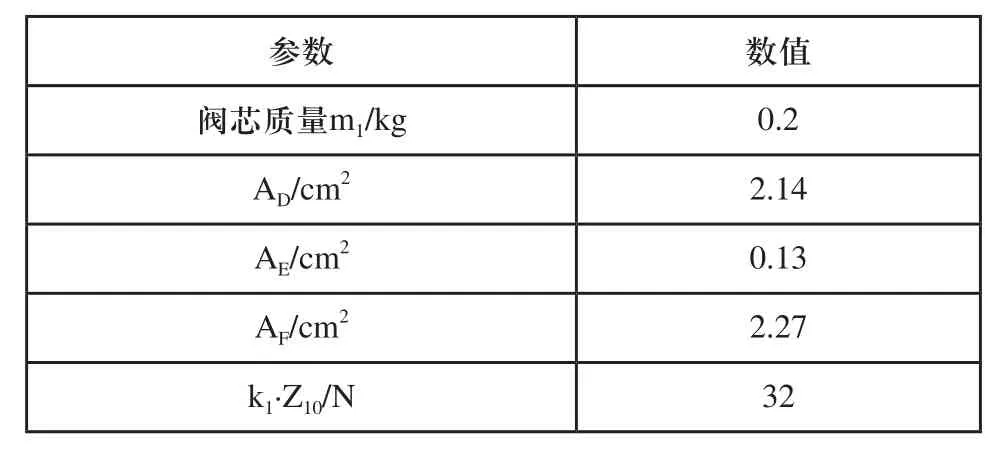
表3 先導插裝閥技術參數(shù)

3.1 基礎振動下插裝閥組的抗振特性分析

在基礎振動（A=0.008m，f=50Hz）與無基礎振動環(huán)境下，插裝閥組主閥芯位移，主閥出口壓力、主閥出口流量的時域變化曲線如圖5至圖10所示。

由圖5、圖6對比可知，基礎振動對兩種閥組主閥芯開啟初期影響不大，這是由于此時插裝閥主閥芯尚未達到穩(wěn)態(tài)平衡，進出油口壓力遠大于閥芯所受彈簧力與振動引起的慣性力，閥芯因此快速上升。在主閥芯開啟初期，二級插裝閥組響應更快，這是由于三級插裝閥組的二級先導閥的開啟導致這一延遲。

伴隨著先導插裝閥在系統(tǒng)壓力作用下迅速開啟，三級插裝閥組主閥控制腔油液通過先導插裝閥迅速排出，在1.8s內達到最大開口度；二級插裝閥組主閥芯開啟速度低于三級插裝閥組主閥芯，在3s內達到最大開口度。三級插裝閥組達到閥芯最大開口度的速度較快，這是因為二級先導閥較大的過流面積，使得控制腔油液在更短的時間內排出。

最后，二級插裝閥組與三級插裝閥組主閥芯均在系統(tǒng)壓力及振動引起的閥芯慣性力等合力作用下達到動態(tài)平衡。

如圖5所示，取閥芯在無振動下穩(wěn)態(tài)開啟高度為X0，如圖6所示，取振動下閥芯的穩(wěn)態(tài)位移波動值為δ，定義主閥芯的波動比值為：

如圖5、圖6可知，在穩(wěn)態(tài)下二級插裝閥組主閥芯的波動比值明顯高于三級插裝閥組主閥芯。

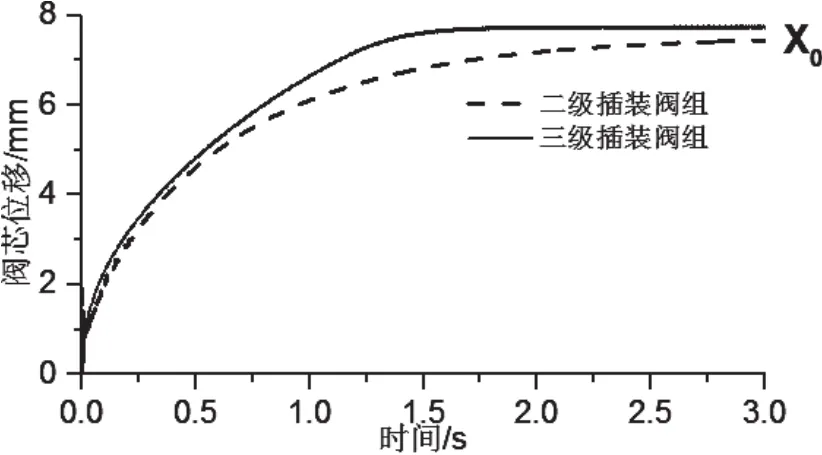
圖5 無基礎振動下閥組主閥芯位移時域變化

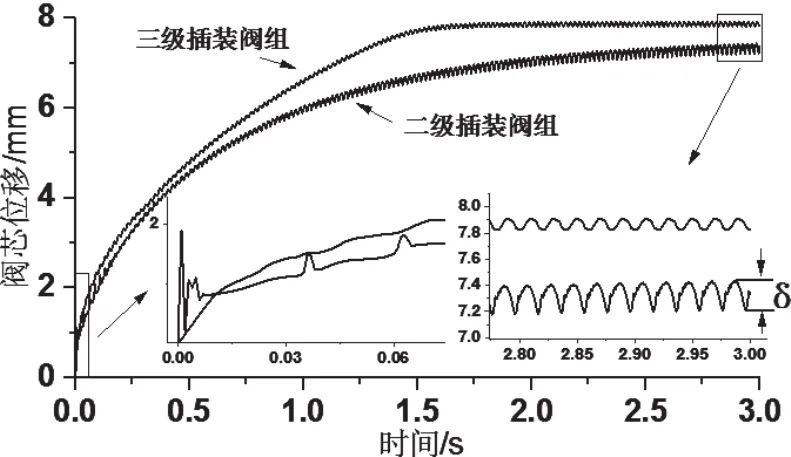
圖6 基礎振動下閥組主閥芯位移時域變化

由圖7、圖8可知，插裝閥組主閥在啟動瞬間，出口壓力會出現(xiàn)較大的壓力超調，而后逐漸過渡到穩(wěn)定狀態(tài)。二級插裝閥組主閥芯開啟初期出口壓力的最大超調量較大，三級插裝閥組主閥開啟更加平穩(wěn)。二者調整時間基本一致，在0.6s左右達到穩(wěn)態(tài)；在基礎振動下，閥組的穩(wěn)態(tài)出口壓力會產(chǎn)生周期性波動，二級插裝閥組穩(wěn)態(tài)出口壓力波動略大于三級插裝閥組。

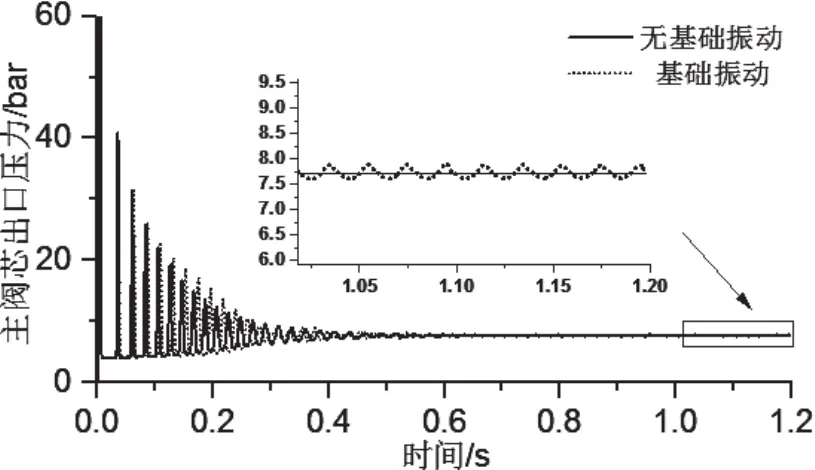
圖7 二級插裝閥組出口壓力

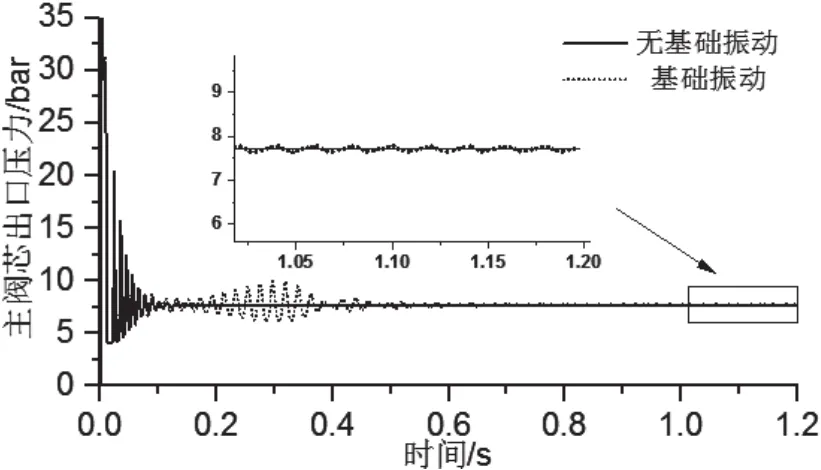
圖8 三級插裝閥組出口壓力

由圖9、圖10可知，閥組主閥在啟動瞬間，出口流量會出現(xiàn)流量超調，而后逐漸過渡到穩(wěn)定狀態(tài)。由于三級插裝閥閥組先導級開啟的延遲性，三級插裝閥組出口流量上升時間略大于二級插裝閥組。三級插裝閥組主閥出口流量波動最大超調量及調整時間較小，出口流量更為平穩(wěn)。在基礎振動的影響下，穩(wěn)態(tài)下閥組出口流量均會產(chǎn)生波動，二級插裝閥組穩(wěn)態(tài)出口流量波動比三級插裝閥組約大于23%。

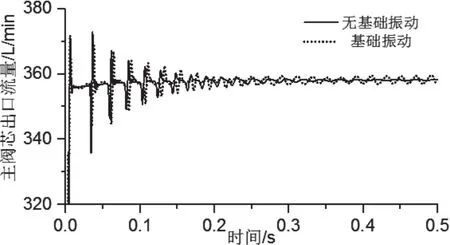
圖9 二級插裝閥組出口流量

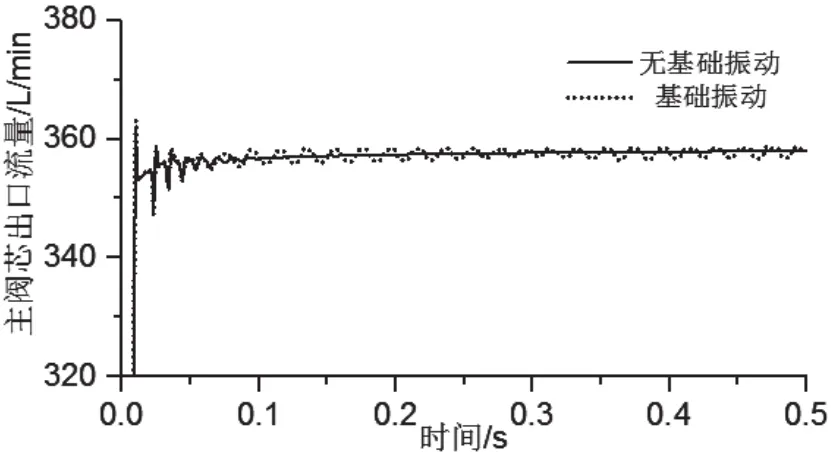
圖10 三級插裝閥組出口流量

結果表明，基礎振動（A=0.008m，f=50Hz）下，二級插裝閥組響應特性更好，三級插裝閥組穩(wěn)態(tài)特性更優(yōu)；基礎振動會引起閥芯的受迫振動，并引起二級插裝閥組與三級插裝閥組主閥芯出現(xiàn)位移波動，進而出現(xiàn)壓力與流量波動。受基礎振動的影響，閥芯位移，閥組出口壓力，閥組出口流量最終在一個恒定值上下波動，其恒定值分別為7.31mm、7.83mm；7.74bar、7.723bar；357L/min、356.7L/min；波動幅值分別為：0.24mm、0.086mm；0.337bar、0.101bar；2.57L/min、2.02L/min；三級插裝閥組在基礎振動下的閥芯位移波動，出口流量波動及出口壓力波動均小于二級插裝閥組；取式(13)閥芯位移波動比值τ為插裝閥組抗振特性主要評價指標。綜上可知：三級插裝閥組在基礎振動（A=0.008m，f=50Hz）下的抗振特性更優(yōu)。

3.2 振動參數(shù)對插裝閥組抗振特性的影響分析

為確定插裝閥組在不同振動參數(shù)下的抗振特性規(guī)律，以二級插裝閥組與三級插裝閥組主閥芯波動比值τ為評定標準。

3.2.1 基礎振動幅值A的影響

圖11為在基礎振動（f=50Hz）下二級插裝閥組與三級插裝閥組主閥閥芯波動比值隨振動幅值的變化曲線。

仿真結果表明，二級插裝閥組與三級插裝閥組主閥芯在隨著基礎振動的幅值增加，閥芯波動比值也隨之增加；在0～5mm基礎振動幅值下的閥芯波動比值均小于0.4%，二者抗振特性基本一致，受基礎振動影響均較小。在振幅大于8mm后，二級插裝閥組主閥芯波動，隨振幅增加而明顯增大，受振動影響較大。三級插裝閥組主閥芯波動也隨振幅增加而增大，但增幅遠小于二級插裝閥組，受振動影響較小，抗振特性更優(yōu)。

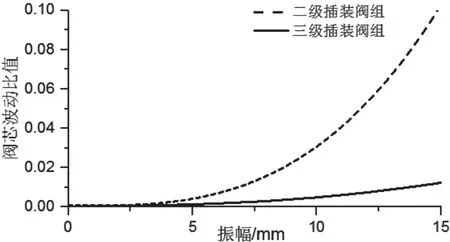
圖11 τ隨振幅變化曲線

3.2.2 基礎振動頻率f的影響

根據(jù)越南某工地TBM掘進工作時，左右兩側撐靴振動頻率實測數(shù)據(jù)顯示，振動頻率集中在100Hz以內。因此，仿真頻率選取在0～80Hz之間。圖12為在基礎振動（f=0.008m）下二級插裝閥組與三級插裝閥組主閥閥芯波動比值隨振動頻率的變化曲線。

仿真結果表明：二級插裝閥組與三級插裝閥組隨著基礎振動頻率的增大，閥芯波動比值也隨之增加，在0～40Hz基礎振動頻率下的均小于0.8%，二者抗振特性基本一致，受基礎振動影響較小；當振動頻率大于50Hz時，二級插裝閥組主閥閥芯波動比值隨頻率變化明顯，抗振特性較差。三級插裝閥組主閥芯波動也隨頻率增加而增大，但閥芯波動比值小于2%，受基礎振動影響較小，表現(xiàn)出更優(yōu)的抗振特性。

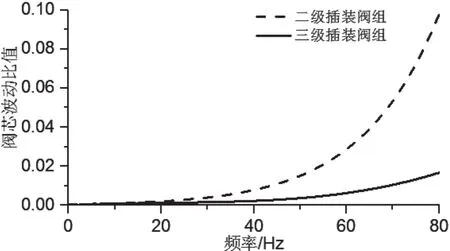
圖12 τ隨頻率變化曲線

4 結論

建立基礎振動下插裝閥組數(shù)學模型，以插裝閥組主閥芯波動比值τ為評定標準，研究分析插裝閥組的抗振特性：

1）基礎振動（A=0.008m，f=50Hz）下，二級插裝閥組響應特性更好，三級插裝閥組穩(wěn)態(tài)特性更優(yōu)；基礎振動會引起閥芯的受迫振動，并引起二級插裝閥組與三級插裝閥組主閥芯出現(xiàn)位移波動，進而出現(xiàn)壓力與流量波動。

2）二級插裝閥組與三級插裝閥組閥芯位移波動比值τ隨基礎振動幅值的增加而增加，隨基礎振動頻率的增加而增加。

3）在基礎振動幅值小于5mm或基礎振動頻率小于40Hz時，二級插裝閥組與三級插裝閥組抗振特性基本一致，受振動影響較小；當基礎振動頻率大于50Hz時，基礎振動幅值大于8mm時，三級插裝閥組抗振特性更優(yōu)，其主閥芯波動比值基本保持在2%以下，受基礎振動影響較小；二級插裝閥組主閥芯波動比值增加明顯，受基礎振動影響較大。