基于PageRank的產(chǎn)品方案設(shè)計(jì)SysML模型關(guān)鍵要素提取方法

蔣丹鼎，趙 穎

（1.國防科技大學(xué) 系統(tǒng)工程學(xué)院，長沙 410073；2.中國航天電子技術(shù)研究院，北京 100094）

0 引言

隨著市場國際化以及企業(yè)間競爭的加劇，企業(yè)必須有快速開發(fā)新產(chǎn)品的能力以應(yīng)對市場需求的不斷變化。相關(guān)研究表明[1]，新產(chǎn)品開發(fā)中約80%的設(shè)計(jì)內(nèi)容需要參考已有的設(shè)計(jì)知識或設(shè)計(jì)成果。從系統(tǒng)工程和已有設(shè)計(jì)成果重用的角度出發(fā)，方案設(shè)計(jì)可以理解為是對已有設(shè)計(jì)結(jié)果中要素的篩選、重用和創(chuàng)新[2]，而要素的篩選往往使用已有設(shè)計(jì)結(jié)果中的關(guān)鍵要素，因此提取出已有設(shè)計(jì)中存在的關(guān)鍵要素并發(fā)掘關(guān)鍵要素間的關(guān)聯(lián)對提高新設(shè)計(jì)的質(zhì)量和效率具有重要意義。

由于當(dāng)前產(chǎn)品的設(shè)計(jì)復(fù)雜高、更新?lián)Q代快，發(fā)掘已有設(shè)計(jì)結(jié)果中的關(guān)鍵要素面臨兩個(gè)方面的問題。一是在產(chǎn)品設(shè)計(jì)結(jié)果中包含要素繁多，難以分析其中要素的關(guān)鍵性；二是產(chǎn)品設(shè)計(jì)結(jié)果中要素間的關(guān)聯(lián)關(guān)系交錯(cuò)復(fù)雜，難以梳理不同要素間的相關(guān)程度。在以往的關(guān)鍵要素提取研究中，MacCalman等人提出了從一個(gè)集成系統(tǒng)模型的試驗(yàn)設(shè)計(jì)中提取關(guān)鍵要素的MBSE方法論[3]，利用試驗(yàn)設(shè)計(jì)探索更大的設(shè)計(jì)空間并了解每個(gè)要素對結(jié)果產(chǎn)生的影響，此方法需要設(shè)計(jì)試驗(yàn)，實(shí)施難度較高；徐蘭依據(jù)貝葉斯原理并利用經(jīng)驗(yàn)數(shù)據(jù)集先驗(yàn)概率得到復(fù)雜質(zhì)量系統(tǒng)中的關(guān)鍵質(zhì)量要素[4]；MaZ采用從機(jī)械對稱結(jié)構(gòu)設(shè)計(jì)實(shí)例數(shù)據(jù)庫中挖掘關(guān)聯(lián)規(guī)則來實(shí)現(xiàn)對結(jié)構(gòu)對稱的設(shè)計(jì)知識在新的設(shè)計(jì)中的重用[5]。但這兩種方法一方面需要使用大量結(jié)果數(shù)據(jù)，難以適應(yīng)產(chǎn)品迭代的速度，另一方面忽略了關(guān)鍵要素間的相互聯(lián)系，不利于關(guān)鍵要素的組合使用。

綜上所述，產(chǎn)品的方案設(shè)計(jì)結(jié)果從整體上可以視為由設(shè)計(jì)要素間相互作用關(guān)系組成的網(wǎng)絡(luò)，關(guān)鍵要素和關(guān)鍵要素間關(guān)聯(lián)的提取就是從上述網(wǎng)絡(luò)中提取出由關(guān)鍵要素組成的子網(wǎng)絡(luò)。與此類似，網(wǎng)頁排名算法的目標(biāo)是從網(wǎng)頁相互引用組成的網(wǎng)絡(luò)中提取高質(zhì)量的網(wǎng)頁，我們可以將高質(zhì)量的網(wǎng)頁看作關(guān)鍵要素，而把與之互聯(lián)的網(wǎng)頁鏈接關(guān)系看作關(guān)鍵要素與其他要素之間的連接。同時(shí)，基于模型的系統(tǒng)工程（model-based systems engineering，簡稱MBSE）及其標(biāo)準(zhǔn)建模語言SysML已經(jīng)成為復(fù)雜產(chǎn)品方案設(shè)計(jì)的重要方法[6～8]，因此本文以產(chǎn)品SysML模型中的關(guān)鍵要素提取為目標(biāo)，借鑒面向互聯(lián)網(wǎng)互聯(lián)網(wǎng)頁排名算法PageRank，提出了設(shè)計(jì)關(guān)鍵要素的提取算法KEERank（Key Elements Extraction with PageRank）。

1 KEERank方法原理

Google PageRank算法的思想精華在于：將一個(gè)網(wǎng)頁級別（重要性）的排序問題轉(zhuǎn)化成了一個(gè)公共參與、以群體民主投票的方式求解的問題，網(wǎng)頁之間的鏈接即被認(rèn)為是網(wǎng)頁間的投票行為[9]。產(chǎn)品SysML模型中關(guān)鍵要素的提取問題與網(wǎng)頁排序問題相同的是需要評價(jià)網(wǎng)絡(luò)中節(jié)點(diǎn)重要性，與網(wǎng)頁排序問題不同的是產(chǎn)品SysML模型中模型元素間的關(guān)系復(fù)雜多樣，難以評估不同關(guān)系對模型元素重要性的影響。根據(jù)上述分析，基于PageRank的產(chǎn)品SysML模型關(guān)鍵要素提取方法主要需要解決以下兩個(gè)問題：一是如何判斷產(chǎn)品SysML模型中模型元素間不同關(guān)系對模型元素重要性評估的影響程度，二是如何在已知不同關(guān)系對模型元素重要性評估影響大小的情況下對節(jié)點(diǎn)重要性進(jìn)行合理評估。

KEERank方法共包含兩個(gè)步驟，第一步是將產(chǎn)品SysML模型轉(zhuǎn)化為有向加權(quán)圖，第二步是利用有向加權(quán)圖評估模型元素的重要性進(jìn)而獲取其中的關(guān)鍵要素。產(chǎn)品SysML模型M可以描述為M=（S，E），其中S表示模型元素的集合，E是模型元素間關(guān)系的集合。產(chǎn)品SysML模型對應(yīng)的有向加權(quán)圖即系統(tǒng)加權(quán)圖可以描述為WG=（S，E，W），其中S和E與M中的S和E相同，W表示權(quán)重集，是E中關(guān)系元素所對應(yīng)的關(guān)系強(qiáng)度。關(guān)系強(qiáng)度的定義如下：

定義1：關(guān)系強(qiáng)度（linkingstrength，簡稱ls）是模型元素間特定類型關(guān)系e的連接強(qiáng)度，說明元素之間關(guān)聯(lián)關(guān)系的強(qiáng)弱。

對于任一類型的模型元素間關(guān)系e∈E都有一個(gè)強(qiáng)度描述函數(shù)來反映其連接強(qiáng)度：ls(e)=a，a∈(0,1]為常數(shù)，表示e的關(guān)系強(qiáng)度值。

KEERank方法的第一步通過計(jì)算模型元素間不同關(guān)系類型所對應(yīng)的關(guān)系強(qiáng)度，從而將產(chǎn)品SysML模型M轉(zhuǎn)化為系統(tǒng)加權(quán)圖WG。為了分析模型元素間不同關(guān)系類型所對應(yīng)的關(guān)系強(qiáng)度，本文運(yùn)用層次分析法對不同關(guān)系所對應(yīng)的關(guān)系強(qiáng)度進(jìn)行計(jì)算。

KEERank方法的第二步是要解決系統(tǒng)加權(quán)圖中節(jié)點(diǎn)重要性的評估問題。關(guān)于有向加權(quán)圖中節(jié)點(diǎn)重要性的評估方法，已經(jīng)存在相關(guān)研究[10]，本文結(jié)合關(guān)鍵要素提取的特點(diǎn)與該研究成果，基于PageRank算法評估產(chǎn)品系統(tǒng)加權(quán)圖中的模型元素的重要性。

2 基于關(guān)系強(qiáng)度的模型轉(zhuǎn)換

產(chǎn)品SysML模型中的九種視圖可以分為需求、功能和結(jié)構(gòu)三個(gè)部分[11]（如圖1所示），需求部分描述了產(chǎn)品的存在價(jià)值，行為部分說明了產(chǎn)品功能的實(shí)現(xiàn)形式，結(jié)構(gòu)部分體現(xiàn)了產(chǎn)品的組成元素及其元素間的作用關(guān)系。三部分雖然各有側(cè)重點(diǎn)，但是結(jié)構(gòu)部分作為行為的載體以實(shí)現(xiàn)產(chǎn)品功能，反映了設(shè)計(jì)結(jié)果中最根本的內(nèi)容，因此下文將針對產(chǎn)品SysML模型中的結(jié)構(gòu)部分進(jìn)行分析。

圖1 產(chǎn)品SysML模型中所包含的視圖分類

產(chǎn)品SysML模型到系統(tǒng)加權(quán)圖的轉(zhuǎn)換需要首先從模型M中獲取元素集合S及其關(guān)系集合E，然后評價(jià)不同模型元素間關(guān)系的關(guān)系強(qiáng)度并進(jìn)而得出系統(tǒng)加權(quán)圖WG中的W集合中的元素，進(jìn)而得到系統(tǒng)加權(quán)圖WG。為了探討產(chǎn)品模型結(jié)構(gòu)部分中模型元素間的相關(guān)關(guān)系，本文根據(jù)文獻(xiàn)[12]將SysML結(jié)構(gòu)圖中模型元素間關(guān)系表達(dá)總結(jié)為5種，如表1所示。

根據(jù)表1，本文對不同模型元素間關(guān)系定義及其方向的說明如下：交互關(guān)系記作ia(si，sj)，根據(jù)建模時(shí)對應(yīng)的接口或流屬性來確定，方向與建模時(shí)表達(dá)方向一致；約束關(guān)系記作cs(si，sj)，方向?yàn)殡p向關(guān)系;引用關(guān)系記作rt(si，sj)，方向與建模時(shí)表達(dá)方向一致；分解關(guān)系記作di(si，sj)，在分解關(guān)系的提取中，復(fù)合關(guān)聯(lián)關(guān)系根據(jù)建模方向拆解為一對或兩對關(guān)系，每個(gè)結(jié)構(gòu)屬性與模塊發(fā)生雙向關(guān)系；依賴關(guān)系記作ro(si，sj)，在關(guān)系提取中，將受某一模型元素影響的模型元素與該模型元素建立依賴關(guān)系，方向與建模時(shí)表達(dá)方向一致。模型元素si指向sj的類型為f的關(guān)系可以描述為其中

為了獲得上述五種關(guān)系對應(yīng)的關(guān)系強(qiáng)度，采用層次分析法實(shí)現(xiàn)計(jì)算，步驟如下:

步驟1：構(gòu)建遞階層次結(jié)構(gòu)模型。如圖2所示，將目標(biāo)層設(shè)為確定不同關(guān)系類型的關(guān)系強(qiáng)度，方案層即為五種關(guān)系，在策略層提出2個(gè)評價(jià)準(zhǔn)則：約束強(qiáng)度F1和元素間距離F2。約束強(qiáng)度指的是關(guān)系能夠體現(xiàn)的兩個(gè)元素間的相關(guān)程度，元素間距離指的是關(guān)系的靈活程度。以分解關(guān)系和交互關(guān)系為例，分解關(guān)系只能作用于有從屬關(guān)系的要素之間，而交互關(guān)系可以聯(lián)系不同層級的系統(tǒng)，相較來說，分解關(guān)系的約束強(qiáng)度高，交互關(guān)系能夠約束的模型元素間距離大。

步驟2：用成對比較法和1-9比較尺構(gòu)造比較矩陣。評價(jià)準(zhǔn)則F1、F2對目標(biāo)的比較矩陣為A，五種關(guān)系對F1、F2的比較矩陣為

表1 SysML模型中的模型元素間相關(guān)關(guān)系提取

圖2 關(guān)系強(qiáng)度評估的層次結(jié)構(gòu)模型圖

表2 評價(jià)因素對目標(biāo)的比較矩陣A

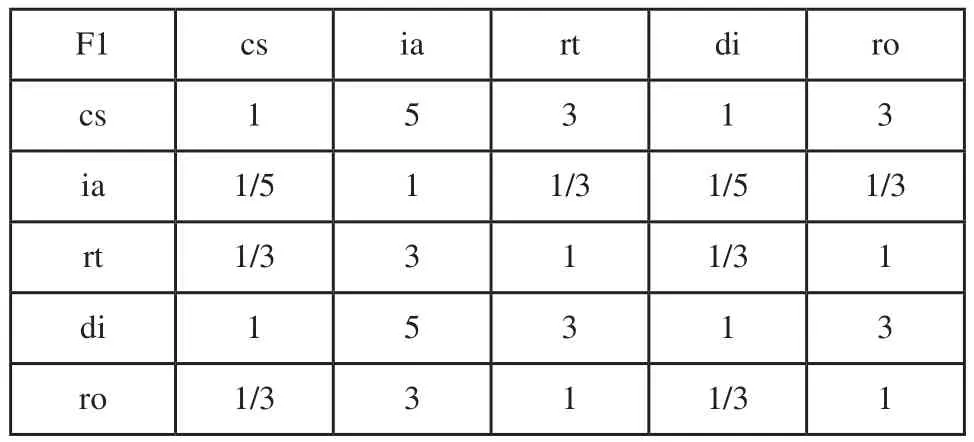
表3 五種關(guān)系對F1的比較矩陣B(3)1

步驟3：計(jì)算單層排序權(quán)向量，并做一致性檢驗(yàn)。對每個(gè)對比較矩陣計(jì)算最大特征值及其對應(yīng)的特征向量，然后根據(jù)計(jì)算一致性指標(biāo)比，其中n為比較矩陣中包含元素的個(gè)數(shù)。比較矩陣A為二階矩陣，滿足一致性要求，其特征向量歸一化后為w(2)=[0.75, 0.25]T。比較矩陣B1(3)和B2(3)計(jì)算結(jié)果如表所示，其中當(dāng)n=5時(shí)，查表得RI=1.12，通過一致性校驗(yàn)。

表4 五種關(guān)系對F2的比較矩陣

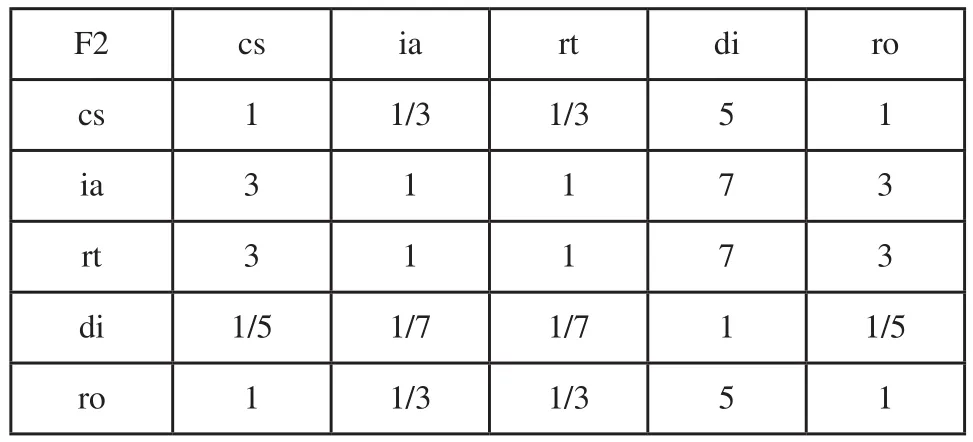
表4 五種關(guān)系對F2的比較矩陣

F2 cs ia rt di ro cs 1 1/3 1/3 5 1 ia 3 1 1 7 3 rt 3 1 1 7 3 di 1/5 1/7 1/7 1 1/5 ro 1 1/3 1/3 5 1

表5 比較矩陣B1(3)和B2(3)的權(quán)向量計(jì)算結(jié)果

表6 五種關(guān)系的關(guān)系強(qiáng)度

計(jì)算出模型元素間不同關(guān)系類型對應(yīng)的關(guān)系強(qiáng)度后，根據(jù)產(chǎn)品SysML模型M中關(guān)系類型E獲得相對應(yīng)的關(guān)系強(qiáng)度，即可生成系統(tǒng)加權(quán)圖WG中的模型元素間關(guān)系強(qiáng)度集合W。

3 基于PageRank的關(guān)鍵要素提取

根據(jù)PageRank算法的原理，評價(jià)模型元素的關(guān)鍵性必須引入鄰接矩陣，然后借助鄰接矩陣建立概率轉(zhuǎn)移矩陣Q，并迭代求解計(jì)算模型元素的重要性，最后調(diào)整權(quán)值從模型元素中篩選關(guān)鍵要素。由于產(chǎn)品SysML模型的特殊性，在使用系統(tǒng)加權(quán)圖構(gòu)建鄰接矩陣時(shí)，有可能存在兩個(gè)模型元素間存在兩個(gè)及兩個(gè)以上關(guān)聯(lián)的情況，因此本文引入了貢獻(xiàn)度的概念來描述鄰接矩陣中兩個(gè)模型元素間的聯(lián)系強(qiáng)弱。

定義2：貢獻(xiàn)度lss是兩個(gè)模型元素間全部關(guān)系所對應(yīng)的關(guān)系強(qiáng)度之和，反應(yīng)了模型元素間的聯(lián)系強(qiáng)弱，計(jì)算方式如下：

其中f(si, sj)是判斷模型元素si到sj是否存在類型為f的相關(guān)關(guān)系，若存在，則f(si, sj)=1，反之f(si, sj)=0。

根據(jù)模型元素間的貢獻(xiàn)度計(jì)算方法將產(chǎn)品系統(tǒng)加權(quán)圖轉(zhuǎn)化為鄰接矩陣M。

以液壓缸系統(tǒng)加權(quán)圖中的部分為例，其鄰接矩陣的構(gòu)建方法如圖3所示，其中鄰接矩陣第i行第j列對應(yīng)的值為以第i行對應(yīng)元素為起始模型元素，以第j列對應(yīng)元素為目標(biāo)模型元素的所有模型元素間關(guān)系對應(yīng)的關(guān)系強(qiáng)度之和，若關(guān)系強(qiáng)度為0，則此處取值為1/n。

圖3 液壓缸系統(tǒng)加權(quán)圖模型(部分)到鄰接矩陣的轉(zhuǎn)換

算法：基于PageRank的關(guān)鍵要素提取。

輸入：系統(tǒng)加權(quán)圖WG。

步驟3：根據(jù)式(3)，迭代計(jì)算設(shè)計(jì)元素的重要度。

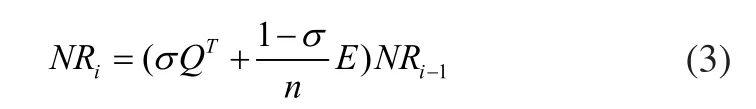
其中，σ(0＜σ＜1)為阻尼系數(shù)，n是模型元素的總個(gè)數(shù)，E為元素全為1的n階方陣。計(jì)算時(shí)取NR0為元素都為1/n的1×n階矩陣。

每次迭代過程會更新NR矩陣的值，等到前后兩次NR值的差值小于某個(gè)接近0的數(shù)時(shí)，結(jié)束迭代過程，此時(shí)NR值對應(yīng)了要素的重要程度。

步驟4：通過動態(tài)設(shè)置閾值σ，從要素中篩選不同層次的關(guān)鍵要素。

表7 液壓缸模型元素間的關(guān)聯(lián)關(guān)系局部

4 驗(yàn)證

以單桿活塞式液壓缸的SysML模型[13,14]為例，本節(jié)首先從系統(tǒng)模型中獲取模型元素集合S和模型元素間關(guān)系集合E，依據(jù)模型元素間不同關(guān)系種類對應(yīng)的關(guān)系強(qiáng)度將SysML模型轉(zhuǎn)化為系統(tǒng)加權(quán)圖，然后根據(jù)模型元素間的貢獻(xiàn)度計(jì)算方式求解出液壓缸系統(tǒng)的鄰接矩陣和鄰接矩陣對應(yīng)的概率轉(zhuǎn)移矩陣，最后使用迭代計(jì)算的方式求解出液壓缸系統(tǒng)中模型元素對應(yīng)的重要度矩陣。其中關(guān)鍵步驟及對應(yīng)結(jié)果如下。

分析單桿活塞式液壓缸的SysML模型提取到的部分模型元素及模型元素間的關(guān)系如表7所示。

計(jì)算模型元素間的貢獻(xiàn)度，并進(jìn)一步得到鄰接矩陣圖如表8所示。

根據(jù)鄰接矩陣構(gòu)建概率轉(zhuǎn)移矩陣Q，并根據(jù)基于PageRank的關(guān)鍵要素提取算法評價(jià)模型元素的重要性，得到模型元素對應(yīng)的NR值，如表9所示。從表8中可以看出，導(dǎo)向套是當(dāng)前液壓缸系統(tǒng)中重要性評價(jià)最高的模型元素，這也反應(yīng)了此液壓缸擁有較高精度的特點(diǎn)。

隨著方案設(shè)計(jì)過程的深入，設(shè)計(jì)者對當(dāng)前系統(tǒng)的關(guān)注將逐漸偏移到重要度較低的要素。因此，我們可以通過動態(tài)調(diào)整關(guān)鍵要素的篩選閾值σ，查看不同層級結(jié)構(gòu)中的關(guān)鍵要素。σ越小表示要查看設(shè)計(jì)要素的重要性越低，就越依賴于其它要素或者該要素對其他要素的影響越弱。例如：圖4和圖5是σ分別取=1.1和0.55所獲得的關(guān)鍵要素可視化圖。在圖4中，壓力P1、P2并不屬于關(guān)鍵要素，隨著設(shè)計(jì)進(jìn)程的推進(jìn)，取較低的閾值之后，在圖5可以看見這兩個(gè)要素。

圖4 σ=1.1時(shí)液壓缸SysML模型中關(guān)鍵要素的分布圖

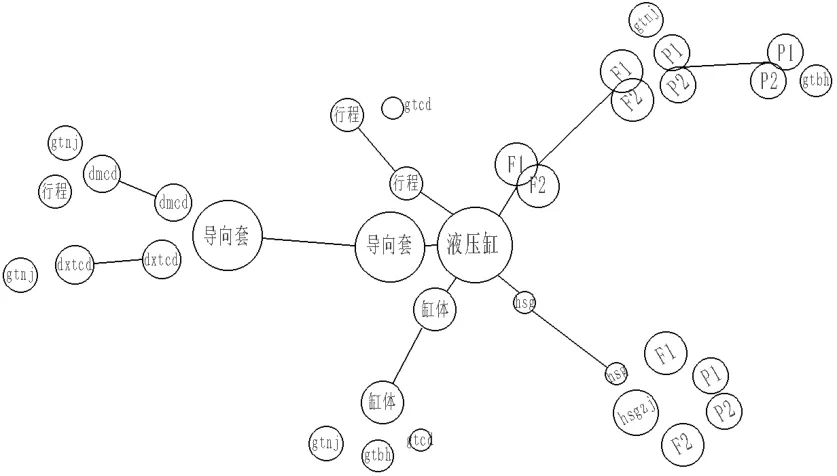
圖5 σ=0.55時(shí)液壓缸SysML模型中關(guān)鍵要素的分布圖

表8 液壓缸產(chǎn)品對應(yīng)的鄰接矩陣（部分）

表9 液壓缸系統(tǒng)模型模型元素及其NR值（部分）

同時(shí)，根據(jù)鄰接矩陣中設(shè)計(jì)要素的關(guān)聯(lián)關(guān)系，我們可以快速地從歷史設(shè)計(jì)結(jié)果中取得與關(guān)鍵要素相關(guān)的其他設(shè)計(jì)要素，更好地分析設(shè)計(jì)變更的傳播影響，從而節(jié)約設(shè)計(jì)者時(shí)間，加快方案設(shè)計(jì)的進(jìn)程。例如，從滿足液壓缸推力設(shè)計(jì)的角度出發(fā)，在表8中提取所有與推力相關(guān)的關(guān)鍵要素及其對應(yīng)的貢獻(xiàn)度如表10所示。

表10 與推力元素F1相關(guān)的關(guān)鍵要素及其貢獻(xiàn)度

5 結(jié)束語

本文提出了一種關(guān)鍵要素的提取方法KEERank，通過將產(chǎn)品SysML模型轉(zhuǎn)化為系統(tǒng)加權(quán)圖，然后利用考慮權(quán)值的PageRank方法來提取關(guān)鍵要素。與仿真方式或者根據(jù)使用結(jié)果反饋結(jié)合概率推算的方式相比，KEERank方法一方面不需要進(jìn)行試驗(yàn)設(shè)計(jì)或者收集反饋信息，另一方面求解速度與上述方法差異不大，因此從總體上來說時(shí)間短、效率高，并且對使用者的要求低，只要具有相應(yīng)的歷史產(chǎn)品SysML模型，就能將模型元素的重要程度評估出來。通過實(shí)例驗(yàn)證可以發(fā)現(xiàn)，關(guān)鍵要素的提取能夠?yàn)樵O(shè)計(jì)人員提供了思考的切入點(diǎn)和優(yōu)化的核心，幫助設(shè)計(jì)者快速理解并重用已有設(shè)計(jì)結(jié)果。

本文中的關(guān)鍵要素挖掘主要針對系統(tǒng)模型中的結(jié)構(gòu)設(shè)計(jì)部分，而需求設(shè)計(jì)與行為設(shè)計(jì)都尚未涉及，未來需要全面研究系統(tǒng)模型，能夠在不同的設(shè)計(jì)階段為設(shè)計(jì)人員提供相應(yīng)的關(guān)鍵要素。此外本文中對于關(guān)鍵要素閾值的設(shè)定尚無有效的方法，有待進(jìn)一步研究。