軸孔裝配工業機器人RBF自適應魯棒控制
(河南理工大學 電氣工程與自動化學院,焦作 454000)
0 引言
工業機器人柔順裝配是工業生產中的重要環節,也是不可或缺的環節。在實際生產應用中具有重要的意義。但是在機器人軸孔裝配中可能會出現卡阻現象,從而造成對機械手末端或者插銷零部件的損壞,嚴重時會造成生產事故。因此,如何避免在軸孔裝配過程中出現卡阻現象,成為了很多學者研究的問題。文獻[1]提出了軸孔裝配過程中的幾何和力學分析,得出軸孔裝配過程中幾個關鍵階段的力學分析。文獻[2]和文獻[3]專門分析了柔順裝配中卡阻和楔緊的力學研究,分析了可能影響卡阻和楔緊的因素,但是并未提出具體的改善方法。文獻[4]分析了間隙、傾角等各種因素對裝配力的影響。文獻[5]提出了基于模糊控制的機器人的柔順裝配的研究,運用模糊控制方法控制位移調整量和旋轉角度調整量來實現柔順插孔作業。文獻[6]提出了工業機器人的機械手的軌跡跟蹤控制,通過自適應滑模控制的不確定性和擾動。
本文中先是對插孔作業中的卡阻現象進行受力分析,找出避免卡阻現象的因素,運用RBF神經網絡魯棒自適應的方法設計出一種力/位混合控制器,實現對機械手末端位置的跟蹤以及末端所受外力的實時跟蹤。
1 卡阻現象的受力分析
在軸孔裝配的過程中,理想的狀態即為水平方向受力為零,而只在豎直方向受力,插銷與插孔的兩側壁均無摩擦力,插銷即可安全出入插孔內。
插孔作業首先要考慮的就是插銷能夠進入孔內,然后才能考慮下面的受力分析,插銷無法入孔有兩種可能,一是插孔定位錯誤,插銷沒有找到插孔的位置,二是插銷所處的姿態使得插銷無法入孔。由于現在幾乎在插銷入孔時都有視覺進行輔助,因此,找不到孔的位置這種情況這里不做考慮,下面分析第二種情況。
一點式接觸階段需要考慮插銷入孔的問題,如果當插銷的一側已經入孔,而另一側底角未進入孔內或者剛好卡在孔的邊緣,此時,插銷不能進入孔中。如圖1所示為插銷不能入孔的臨界情況。
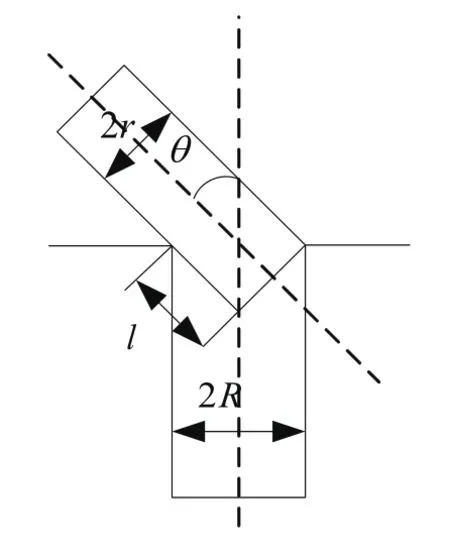
圖1 插銷不能入孔的臨界情況
其中R為插孔的半徑,r為插銷的半徑,l表示插銷進入空的深度。
根據圖1建立三角關系式:
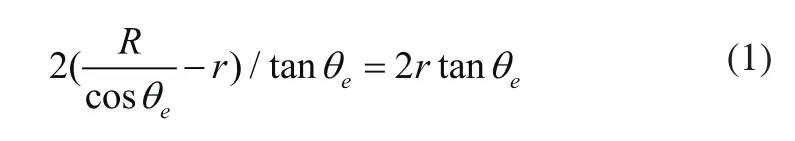
解得:

2 裝配機器人控制方案設計
當插銷進入插孔后,由于軸孔定位時的誤差,插銷的中心軸線與插孔的中心軸線出現一定的夾角,從而造成卡阻現象。
2.1 去卡阻控制方案
當夾持插銷的機械手處于某一狀態時,插銷與插孔的最大靜摩擦力小于于插銷在豎直方向的受力時,此時插銷可以繼續插入。插銷與插孔的最大靜摩擦力大于插銷在豎直方向的受力時,此時插銷將會處于卡阻狀態。由于最大靜摩擦力fmax的大小與水平方向上插銷對插孔的壓力有關,因此,它與插銷所處的姿態有關,即和偏轉角相關。當出現卡阻狀態時,可以通過調整機械手位姿,從而調整插銷的位姿,來保證插銷順利的插入孔內。
因此該插銷去卡阻的工程問題可以轉化成機械手的軌跡跟蹤問題,把從卡阻點作為初始點,平移旋轉后的點作為結束點,規劃出一條機械手的運動軌跡,根據機械手的逆運動學求解,即可以得到各個關節角的運動軌跡。因此只需要設計出一個控制器,使得機械手可以沿著期望軌跡運動,即可以實現插銷入孔作業中的去卡阻問題。
2.2 裝配機器人魯棒自適應控制
實際應用中,要求工業機器人的末端效應器以一定的約束力保持在某一物體表面上。機械手與典型的剛性環境接觸時,存在兩種約束力:一種是末端效應器與約束面接觸點產生的法向接觸力,由于它不產生虛功,所以又稱為無功約束力;另一種是末端效應器與約束面產生的摩擦力,由于它對外做功,所以稱為有功約束力。當機械手在一個有摩擦的剛體表面上滑動時,要同時考慮有功和無功兩種約束力。為簡化問題的分析,本節假設機械手的接觸面是剛性、無摩擦的,即忽略有功約束力,僅研究機械手與剛性接觸面之間的法向完整約束力[7]。n自由度機械手完整的動力學模型可表示為:
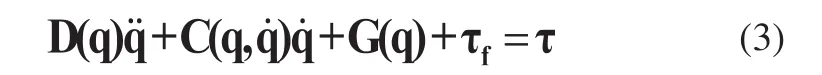
為設計魯棒穩定的控制器,我們需要做一些合理的假設:
假設1:末端機械手的參數矩陣都是有界的;
假設2:期望的系統廣義坐標向量qd連續有界,并具有連續可微的二階導數;
假設3:期望的約束力τf有界。
考慮系統存在的參數不確定性和外界擾動,設計一個RBF神經網絡魯棒自適應控制器,使系統的所有參數一致有界,系統的廣義坐標和速度漸進跟蹤期望的軌跡與速度,約束力趨近期望的有限值。
RBF網絡算法為:
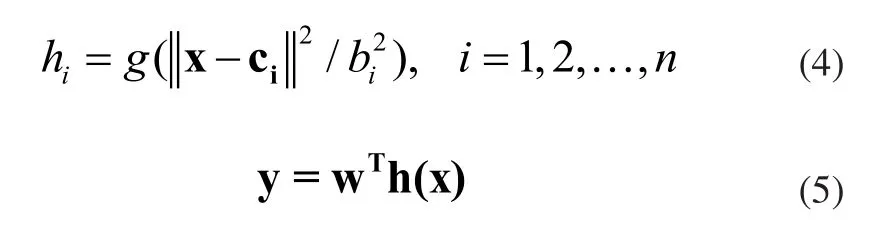
其中,x是輸入向量;y是神經網絡輸出;h=[h1,h2,…,hn]T為高斯函數的輸出;w為神經網絡的權值。ci和bi為高斯函數的參數。
給定一個很小的正數ε和一個連續的函數則存在一個理想的權值向量w*,使得RBF逼近且滿足:
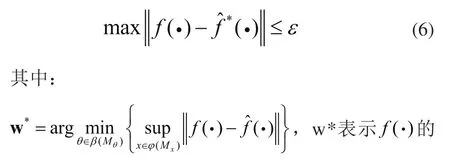
最佳逼近權值。
定義逼近誤差為:
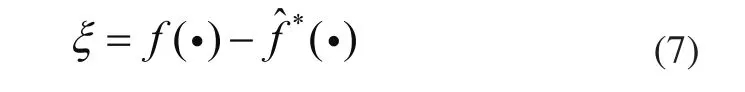
假定逼近誤差ξ有界的,即:
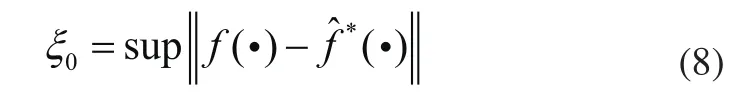
則:
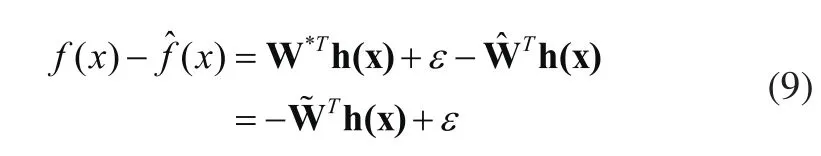
設狀態向量q的期望向量為qd。系統的跟蹤誤差為e=q=qd,定義系統的濾波誤差向量分別為及:
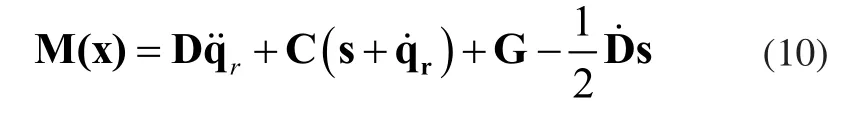
和控制器。
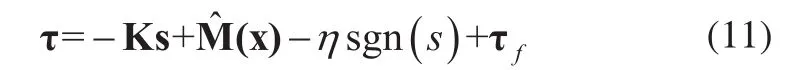
自適應律:

定理:假設機械手的所有參數都是不確定的,外界擾動有界,那么控制器式(11)和自適應律式(12)保證下列結論成立:
跟蹤誤差e以及其微分e˙漸進收斂于0,廣義坐標向量q以及其微分漸進收斂于期望軌跡qd和
證明:定義Lyapunov函數:
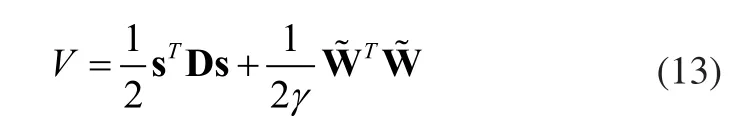
對等式兩邊求微分得:
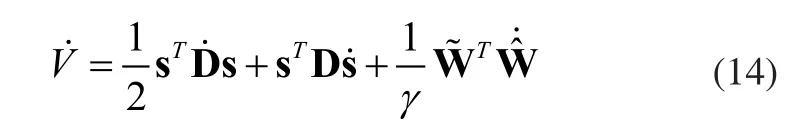
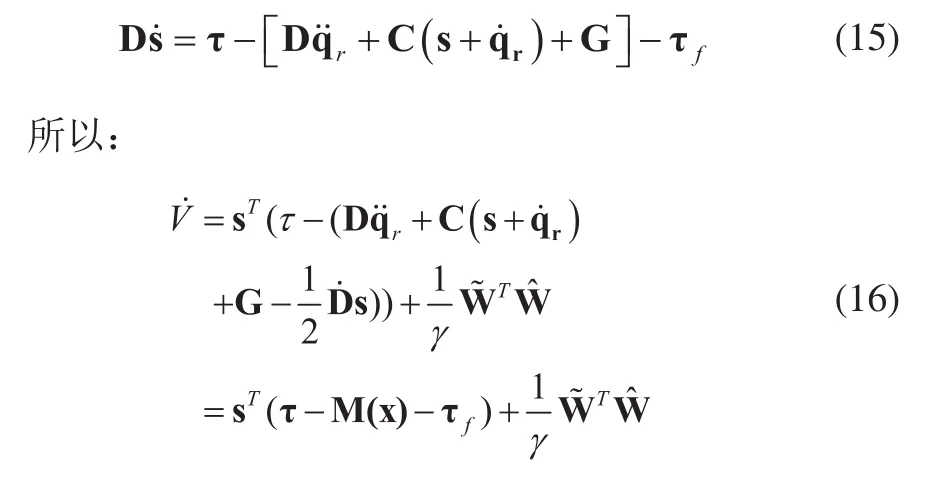
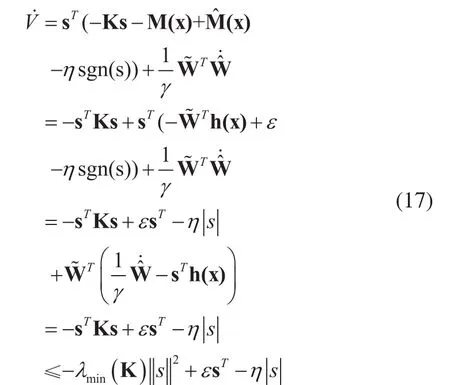
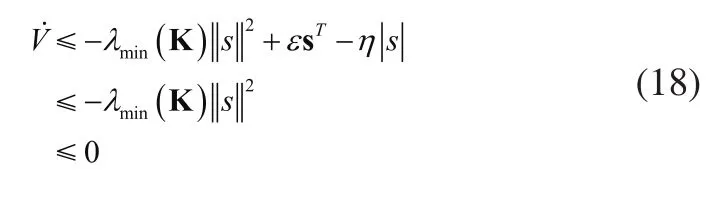
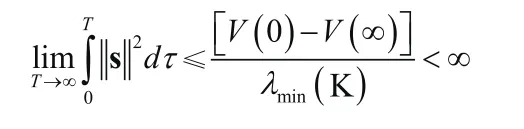
所以,s∈L2。由于所以,由假設2,假設3和qr的定義可以得出,都是有界的。因此,式(10)的右邊有界,則進而得出,由Barbalat定理可得:
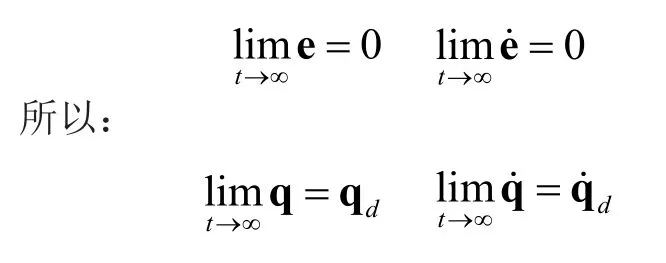
3 位姿跟蹤及約束力跟蹤仿真
選二關節機器人系統,其動力學模型如式(3)所示。
其中:
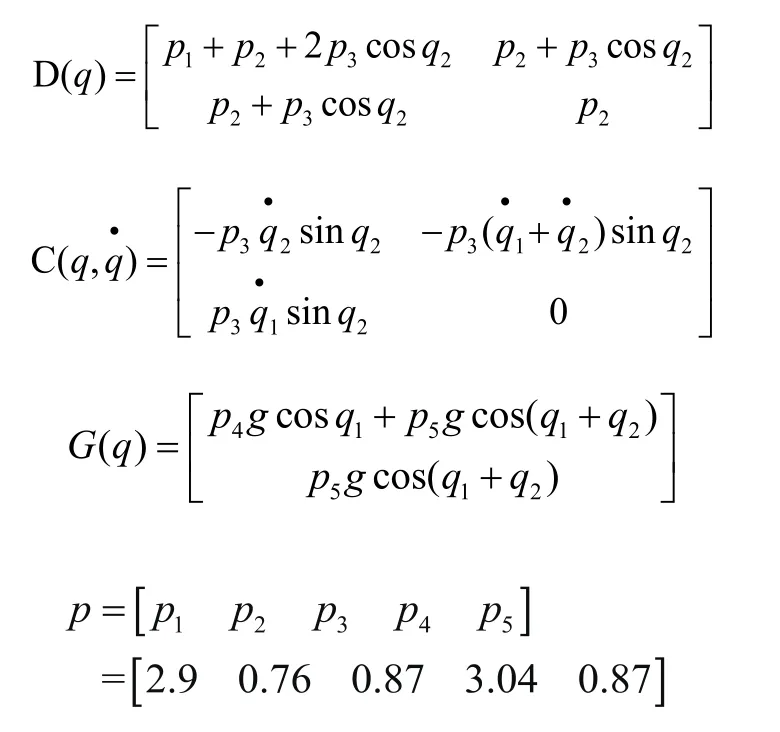
系統的初始狀態為[1.4 0 1.6 0],兩個關節的角度指令分別是qd1=1.4+0.5cost,qd2=1.6+0.5cost;
控制參數取K=diag{20,20},Λ=diag{5,5},ε=0.2,η=10。

bi=0.2,理想約束力τf=5sint。
仿真結果如圖2~圖4所示。
由圖2和圖3可以看出,機械手位置軌跡跟蹤效果良好,能夠實時的控制機械手的關節角度,從而來調整插銷的位姿。由圖4可以看出,該控制器實現了對力信息的實時跟蹤,從而保證機械手對插銷的作用力在未達到插銷與插孔的最大靜摩擦力之前,可以適當的調整插銷的位姿,從而避免出現卡阻現象。
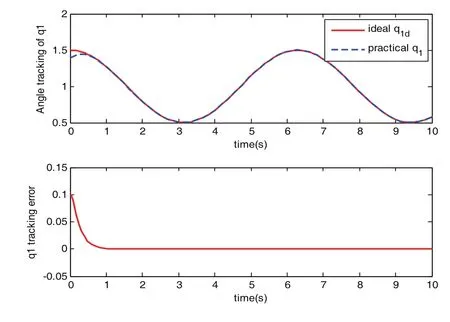
圖2 關節1的角度跟蹤及跟蹤誤差
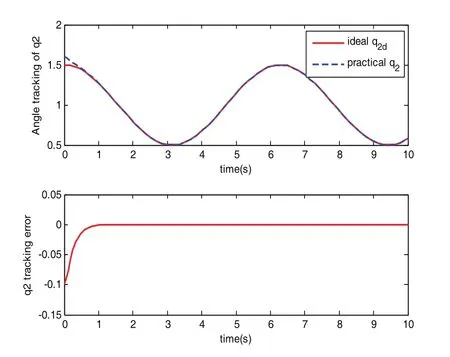
圖3 關節2的角度跟蹤及跟蹤誤差
4 結束語
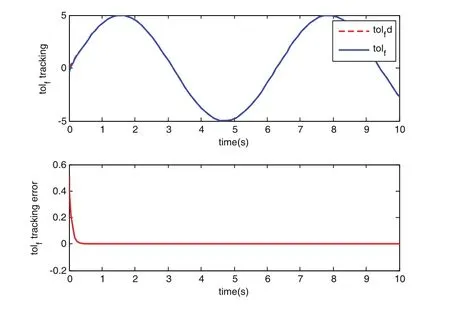
圖4 外界作用力跟蹤及跟蹤誤差
本篇文章詳細的分析了無倒角軸孔作業的整個流程,設計出一種控制方法,可以使得末端機械手通過自身運動,使得裝配過程中避免卡阻現象,并通過仿真證明這種控制方法。由于本次仿真只是運用最基本的二連桿模型進行仿真,然而,在實際的生產應用中經常會出現多個機械手進行配合同時作業,以及在工作空間中的環境約束等,因此,該控制器仍然有待進一步提高。

