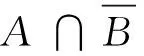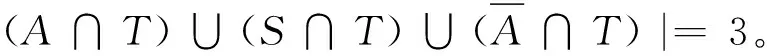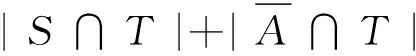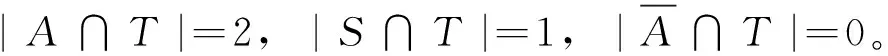不含某類子圖的k-連通圖中的一個結果
(1、2.安順學院數理學院, 貴州 安順561000)
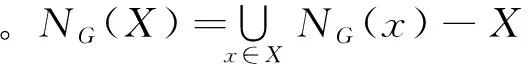
設G是一個k-連通圖,T?V(G) 是V(G)的一個子集。如果G-T至少有兩個連通分支,就稱T為G的一個點割集,簡稱點割。進一步地,若|T|=k,則稱T為G的一個k-點割或最小點割。
設G是一個k(≥2)-連通圖,e=uv∈E(G)是G中的一條邊。對邊e進行如下操作:先去掉邊e,再將e的兩個端點u,v合并為一個頂點,然后將由此產生的所有的“二重邊”用一條“單邊”來替代,這樣,得到一個新圖G′。顯然,由此得到的新圖G′仍然是一個簡單圖。稱e的這種運算為e的收縮(或者稱為“收縮邊e”)。如果收縮k(≥2)-連通圖G中的邊e后仍然得到一個k-連通圖,那么稱e為G的一條k-可收縮邊,簡稱可收縮邊。否則,稱e為的一條不可收縮邊。一個不含任何可收縮邊的非完全k-連通圖稱為收縮臨界k-連通圖。設G是一個非完全k(≥2)-連通圖。顯然,若邊e=uv∈E(G)是G的一條不可收縮邊,當且僅當存在G中的一個最小點割T使得{u,v}?T。
設G是一個k-連通圖,e是G中的一條不可收縮邊,于是存在G中的一個k-點割T,使得e∈E(G[T])。此時若C是G-T的一個連通分支,則稱C為G中一個關于e的連通分支。設Y?E(G)為E(G)的一個非空子集,T為G中的一個k-點割,若E(G[T]) 中含有Y中的某一條邊,這時稱G-T的任一個連通分支C為G中關于Y的連通分支。
若一個圖G沒有子圖同構于圖H,稱G是一個“不含H的圖”。同時稱H為G的一個“禁用子圖”。
1 一些相關結論
1981年,Thomassen[2]證明了下面的定理:
定理1 一個不含三角形的k-連通圖含有一條k-可收縮邊。
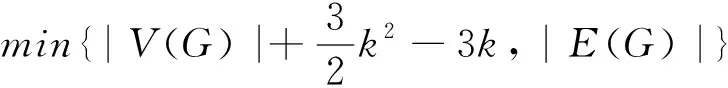
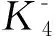
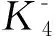
Ando等[5]證明了如下定理:
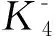
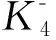
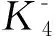
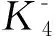
(i) 若δ(G)≥k+1,則G中每一個點都關聯一條k-收縮邊;
(ii) 若G中任意兩個相鄰的點x,y都滿足dG(x)+dG(y)≥2k+1,則G中的每一個k度點都關聯一條k-可收縮邊。
由定理4(ii),我們立即可推出下面的結論:
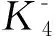
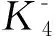
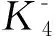
這里需要說明的是,盡管Ando等[5]在證明過程中假定了k≥4為偶數,實際上當k>4為奇數時,該證明(對命題2)仍然有效,命題2的結論仍然正確。故在命題2中對k(≥4)不再限制其奇偶性。實際上,對命題 2,可以將整數考慮到k≥3。于是,進一步地,有下面的結論(在此不妨稱其為定理 5)。
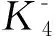
2 定理 5 的證明
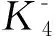
斷言1 若dG(x)=3,則|E(x)∩M|≥1。若|E(x)∩M|=1,設xy∈(E(x)∩M),則xy是G中的一條3-可收縮邊。
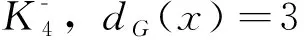
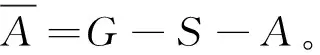
定理 5 的證明。
令F=E(x)∩M。則當dG(x)≥4時,由題設條件總有|F|≥2。當dG(x)=3時, 若|F|=1,由斷言1可知x關聯一條可收縮邊,這時,結論正確。于是,當dG(x)=3時,總假定|F|=3。這樣,無論何種情形,總有|F|≥2。
證明E(x)中至少含有一條3-可收縮邊:
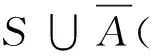
|A∪S|≥|NG(a)∪NG(b)|=|NG(a)|+
|NG(b)|-|NG(a)∩NG(b)|≥3+3-1=5。即,
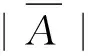
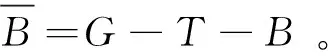
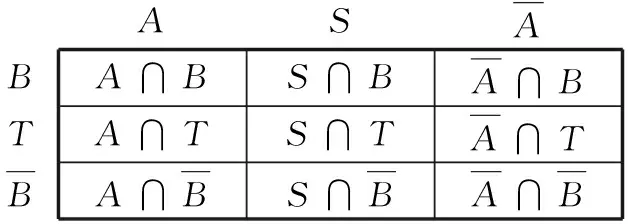
ASABTBA∩BS∩BA∩BA∩TS∩TA∩TA∩BS∩BA∩B
圖1
首先證明A?T。