變流量工況下小型離心壓氣機多目標優化設計

唐新姿 肖 鵬 蔡 鵬 彭銳濤

湘潭大學機械工程學院，湘潭，411105

0 引言

離心壓氣機尺寸小、結構簡單緊湊、單級增壓比高，被廣泛應用于渦輪增壓器、小型燃機等設備。小型離心壓氣機在實際應用中需要經受多工況考驗，追求高效率、高壓比和寬工作裕度，一直是當前壓氣機設計研究的熱點。

國內外學者針對壓氣機氣動性能分析與優化做了大量工作。文獻［1］采用數值計算方法研究了多工況下不同葉頂間隙尺寸對離心壓氣機性能的影響及規律。文獻［2］考慮熱負荷及機械負荷對軸流壓氣機影響，建立了多級軸流壓氣機不同工況葉尖間隙的預估模型。文獻［3］采用數值優化方法對跨聲速軸流壓氣機轉子葉片進行多工況氣動優化設計。文獻［4］利用K riging模型優化壓縮機壓比、效率和整機聲功率級。文獻［5?6］采用神經網絡和多目標遺傳算法對離心空壓機效率和壓比進行優化。文獻［7］結合近似函數方法與遺傳算法，在整機環境下對壓氣機下游轉子進行了優化設計。文獻［8?10］在設計工況下，基于響應面模型、徑向基函數與多目標遺傳算法對離心壓氣機進行優化。上述研究多采用數值計算與遺傳算法對設計工況下的性能進行優化，對變流量的多工況離心壓氣機優化研究相對較少。由于小型離心壓氣機轉速較高，內部流動復雜，單工況設計可能導致非設計工況性能急劇惡化，同時涉及的設計參數較多，因此亟需尋找一種快速高效、綜合考慮變流量工況的優化策略。

本文以某小型離心壓氣機葉輪為研究對象，基于數值計算求解葉輪氣動性能，研究葉輪設計參數對變流量工況氣動性能的影響規律；基于相關性分析，建立降階的優化設計變量空間，采用拉丁超立方試驗設計、K riging模型和NSGA?Ⅱ算法對離心壓氣機進行變流量工況多目標優化。

1 研究對象、數值計算方法及驗證

以某款離心壓氣機葉輪（有6個主葉片和6個分流葉片）為對象，其結構如圖1所示，主要結構參數如下：進口處內徑12mm，進口處外徑29.5mm，葉輪出口直徑50mm，葉片進口角21.6°，葉片出口角55°，包絡角60°，葉頂間隙0.3mm；葉輪設計流量為0.05 kg/s，轉速為135 246 r/m in。

圖1 壓氣機初始葉輪三維模型Fig.1 Th ree d im ensionalm odel of initial com p ressor im peller

考慮節省計算資源，葉輪內部流場和氣動性能計算采用單流道周期性邊界模型，基于Spalart?A llmaras湍流模型求解三維Navier?Stokes方程，空間離散采用中心差分格式，時間離散采用4階Runge?Kutta法。單流道網格拓撲結構如圖2所示，主流通道內的網格采用O 4H拓撲結構，葉頂間隙采用蝶形結構網格，葉片表面第一層網格高度為1μm。經過網格無關性分析，確定網格數約為200萬。進口給定絕對總溫、總壓，出口給定靜壓，葉片和輪轂為旋轉無滑移固壁面，輪蓋為靜止固壁面邊界。

圖2 葉輪風格拓撲結構Fig.2 M esh topology of im peller

為驗證數值計算方法的正確性，選用LSCC離心壓氣機葉輪［11］進行實驗。應用上述數值計算方法，分別求解該葉輪在轉速為1 862 r/m in、流量分別為30 kg/s和23.6 kg/s的設計工況和非設計工況下的氣動性能，并將其與實驗值進行對比分析。

表1所示為該葉輪不同工況下壓比和效率的計算值和實驗值。由表1可知，在設計工況下，壓比和等熵效率的計算值和實驗值的相對誤差分別為-1.0%和-0.2%；在非設計工況下，壓比和效率的計算值和實驗值的相對誤差分別為-0.9%和-1.2%，壓比和等熵效率計算相對誤差均在2%內，即計算值與實驗值基本一致，表明所采用的數值方法是正確可行的。

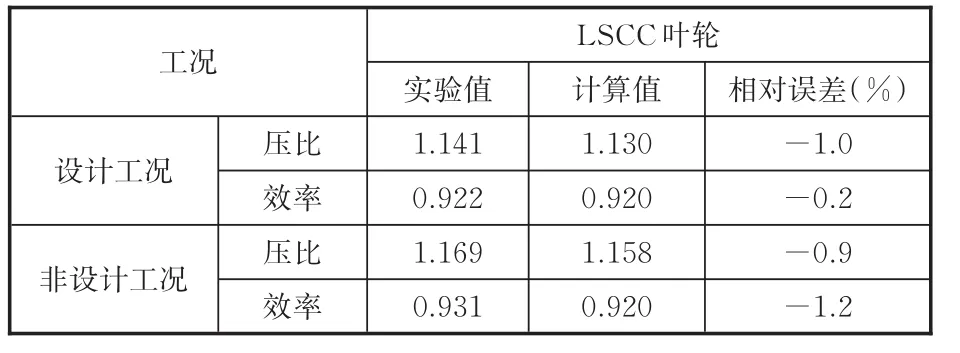
表1 葉輪不同工況下實驗值和計算值Tab.1 Experim entaland calculated values of im peller under differentworking conditions

LSCC葉輪性能曲線如圖3所示，由圖3可知，計算所得的壓比性能曲線與實驗所得壓比性能曲線發展趨勢一致。實驗所得的壓比值為計入了擴壓器增壓后的總壓值，而計算值為不含有擴壓器部分的增壓值，因此計算值比實驗值偏小且最大相對誤差不超過1.8%。由效率性能曲線對比可知，在設計流量時，效率計算值與實驗值基本吻合；喘振邊界點的計算效率較高；大流量工況下，計算所得效率性能曲線與實驗所得效率性能曲線發展趨勢基本一致，由于計算葉輪與實驗葉輪進出口延伸長度不同，高估了進出口流動損失，使得計算值比實驗值總體偏小且最大相對誤差不超過1.5%。綜上所述，總體性能偏差最大相對誤差均在2%以內，滿足工程計算精度要求。

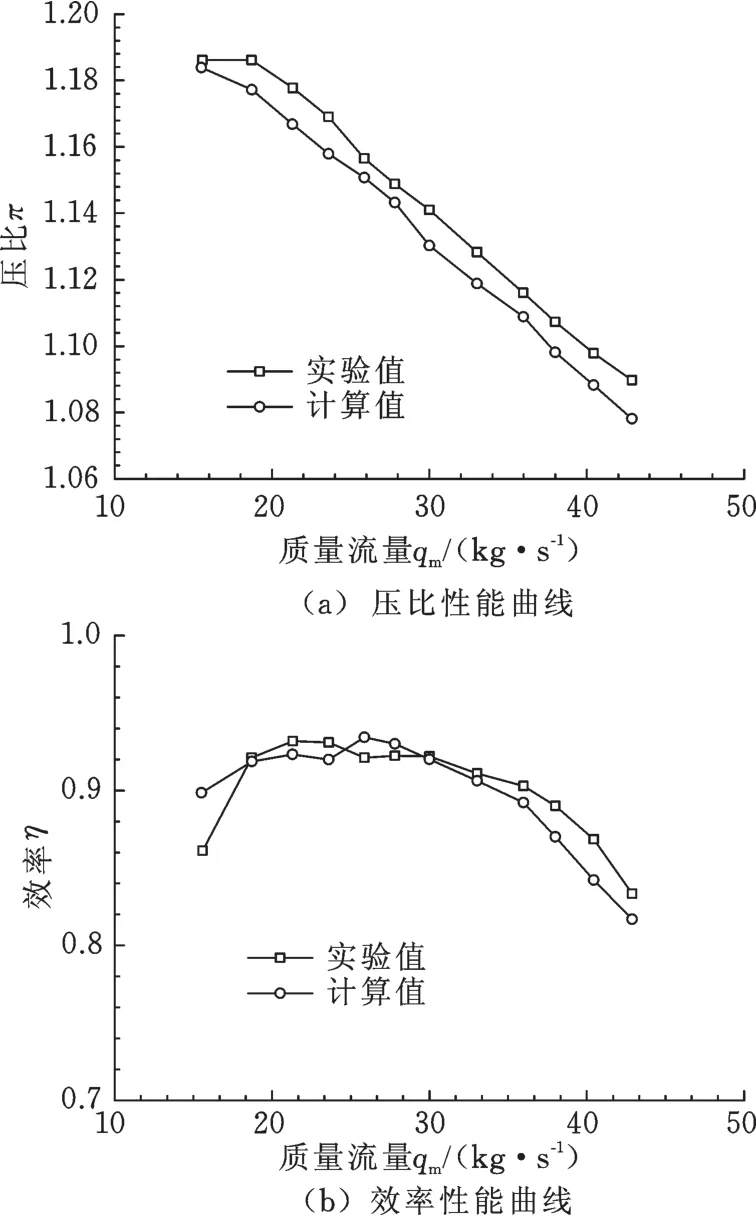
圖3 LSCC葉輪性能曲線Fig.3 LSCC im peller perform ance curves

2 葉輪幾何參數對變流量性能的影響

2.1 葉片進口角對性能的影響

為研究葉片進口角（構造角）對葉輪氣動性能的影響，采用已驗證的數值分析方法，對葉片進口角分別為20°、30°、40°的三組不同葉輪進行對比分析。圖4所示為不同葉片進口角的性能曲線。由圖4可知，隨著葉片進口角的增大，其壓比和效率都會降低，性能曲線整體向下偏移。在設計流量下，葉片進口角從20°增加到40°，效率降低3.2%，壓比降低2.6%。葉片進口角β1b與氣流進口角β1和氣流攻角i之間滿足關系i=β1b-β1，當葉片進口角β1b增大時，氣流攻角β1增大，氣流在進入葉輪時與葉片產生嚴重沖擊，在入口處引起邊界層流動分離，增大了葉輪流動損失，同時分離流向出口處擴大，影響葉輪做功能力，使得效率壓比下降。需要指出的是，在大流量下氣流進口角β1變大，葉片進口角β1b增大，效率增大或減小都有可能存在。

2.2 葉片出口角對性能的影響

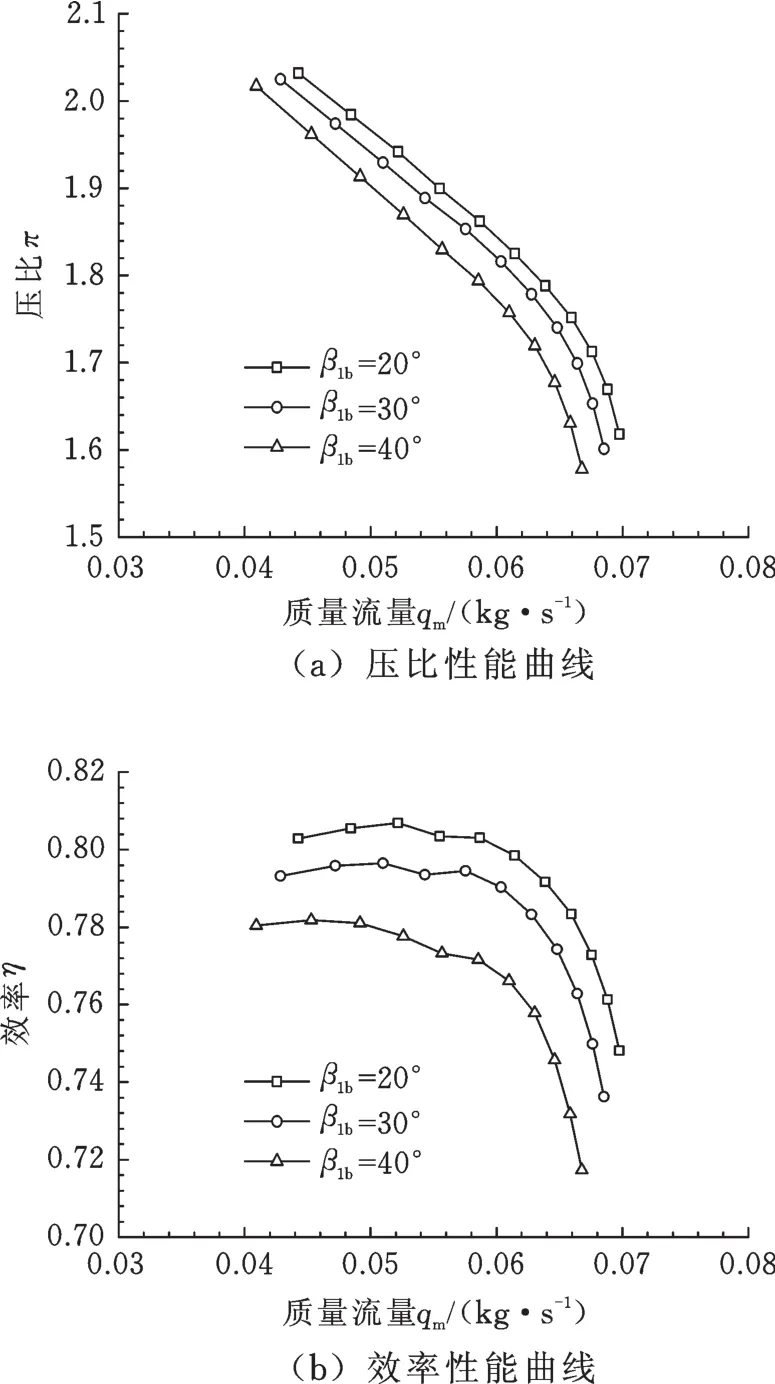
圖4 不同葉片進口角對性能的影響Fig.4 In fluence of in let angles on per form ance of differen t blades

圖5給出了不同葉片出口角β2b對性能的影響。由圖5來看，葉片出口角增大，壓比增大，而其對效率的影響需要根據具體情況確定。對比壓力曲線，葉片出口角由45°增大到65°時，設計流量壓比提高了12%；隨著流量的增加，壓比提高幅度減小。對比效率曲線，葉片出口角由45°增大到55°效率在小流量下提高1.3%，在大流量下基本不變；當葉片進口角由55°增大到65°時，效率在全流量范圍內反而出現下降且最大下降1.3%。葉片出口角增大的主要作用是增加葉輪壓力能，出口葉片角增大會使壓氣機性能曲線往右上方偏移，能得到更寬的工作區域和更好效率。但是葉片出口角的取值過大，會使葉輪出口速度分布很不均勻，導致擴壓器入口處進氣條件的惡化，使得整級效率降低。

2.3 葉片出口寬度對性能的影響

圖6所示為不同葉片出口寬度b2的性能曲線。由圖6可知，增大葉片出口寬度，壓比性能曲線整體向上偏移，在大流量工況下，其效率受出口寬度變化的影響較為明顯。出口寬度從2.05mm增加到2.23 mm時，壓比最大增加9%，效率最大提高5.5%；而出口寬度從2.23mm增加到2.50mm時，壓比最大增加12%，效率最大提高6.4%。葉片出口寬度增加，減小了背流損失，葉輪的失速和堵塞流量增大，增強了葉輪大流量工況適應性。

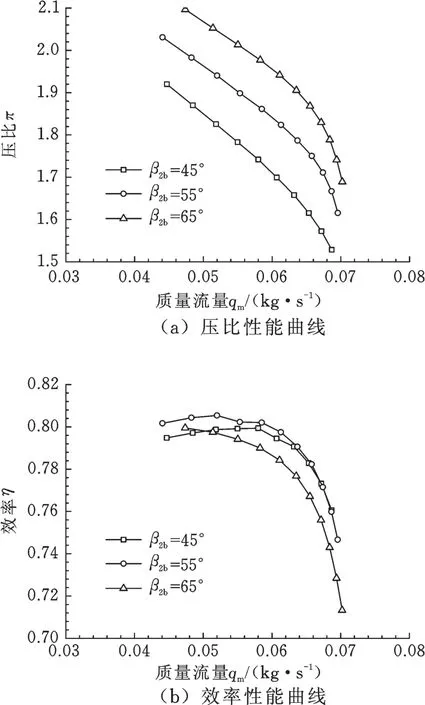
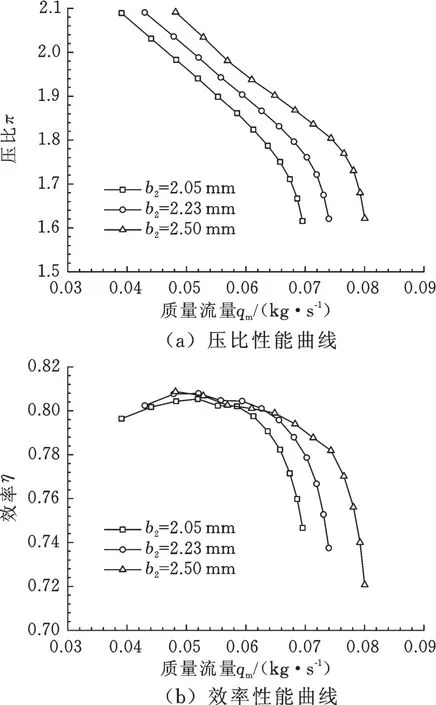
圖6 不同出口寬度對性能的影響Fig.6 Influence of d ifferent ou tlet w idths on performance

2.4 葉頂間隙對性能的影響

圖7所示為不同葉頂間隙t對性能的影響規律。由圖7可以看出，隨著葉頂間隙的增大，葉輪總體性能明顯下降。當葉頂間隙從0.1 mm增加到0.3 mm時，喘振流量點左移34%，同時堵塞流量點左移5%；當葉頂間隙從0.3 mm增加到0.5 mm時，壓比最大減小5.6%，效率最大減小6.6%。葉頂間隙增大，泄漏損失增大，導致效率和壓比下降，同時喘振點和堵塞點提前。

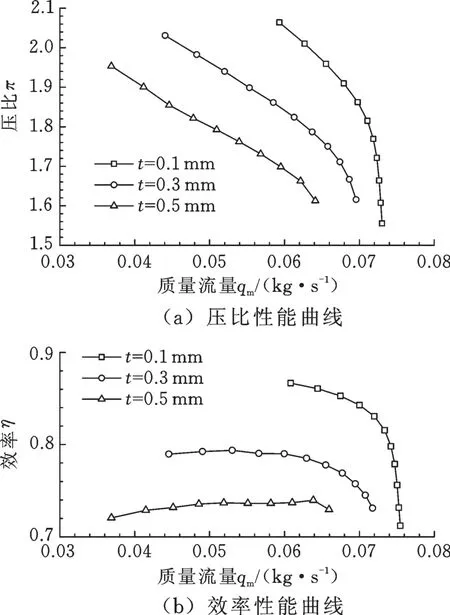
圖7 不同葉頂間隙對性能的影響Fig.7 Effectsof different tip clearance on p roperties

2.5 葉片包絡角對性能的影響

圖8所示為不同葉片包絡角δu對性能的影響。由圖8可知，隨著葉片包絡角的增加，葉輪壓比曲線整體下降，效率在大流量下明顯降低，在小流量下降低不明顯且在喘振流量點反而有所增加。葉片包絡角從50°增加到56°時，壓比最大降低6.1%，效率最大降低4.4%；包絡角從56°增加到60°時，壓比最大降低4.2%，效率最大降低3.3%。出現上述規律的原因主要是，由于包絡角增大，流道增長，從而使得氣流沿程黏性摩擦損失增大；但在小流量時，包絡角增大，葉輪對氣流約束能力增強，流動分離減弱，減小了流動損失。

2.6 分流葉片周向位置對性能的影響

圖9給出了不同周向位置θ對性能的影響規律。由圖9可知，當分流葉片處于居中的位置，其效率和壓比性能曲線都呈現最佳的分布。當分流葉片位于偏向主葉片吸力面35%位置時，壓比最大降低10%，效率最大下降2.6%；隨著分流葉片往主葉片壓力面偏移，位于65%位置時，壓比最大降低2%，效率最大下降6.6%。這是由于分流葉片靠近主葉片吸力面側時，可以抑制主葉片吸力面處的低能流體，改善靠近吸力面側通道流動，但使得靠近壓力面側通道擴散度增加，分流葉片吸力面低能流體面積增加，出現流動分離，使得該通道內流場嚴重惡化，使壓氣機整體性能下降；當分流葉片偏向主葉片壓力面側時，使得整體性能下降。

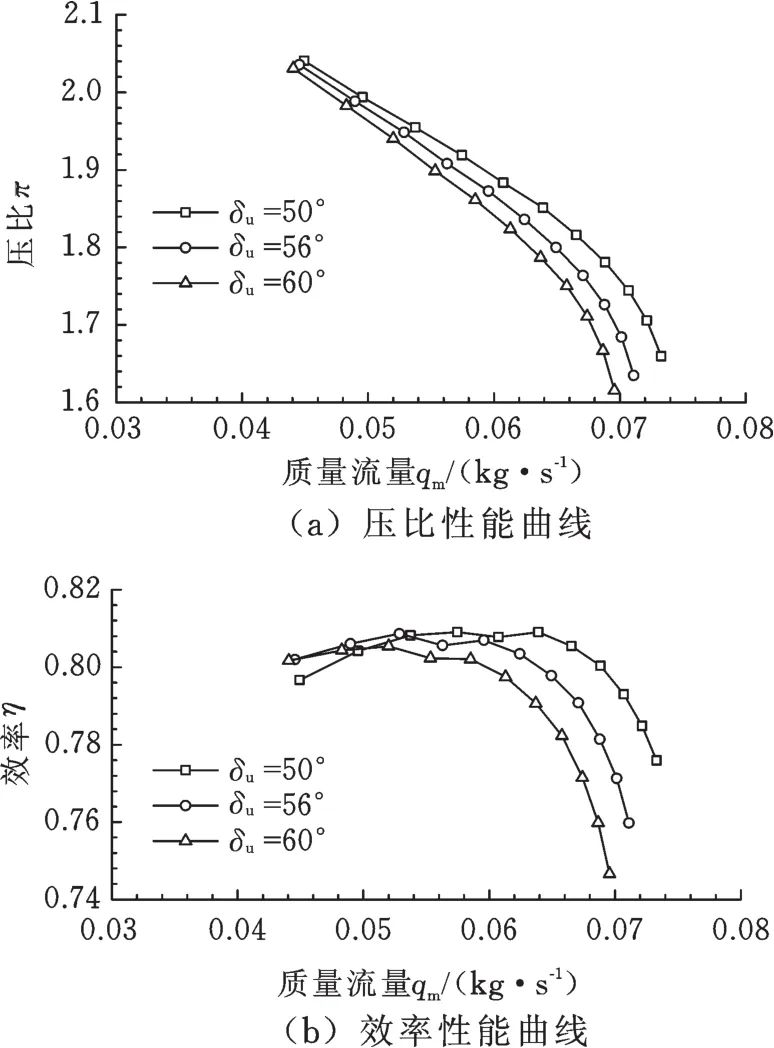
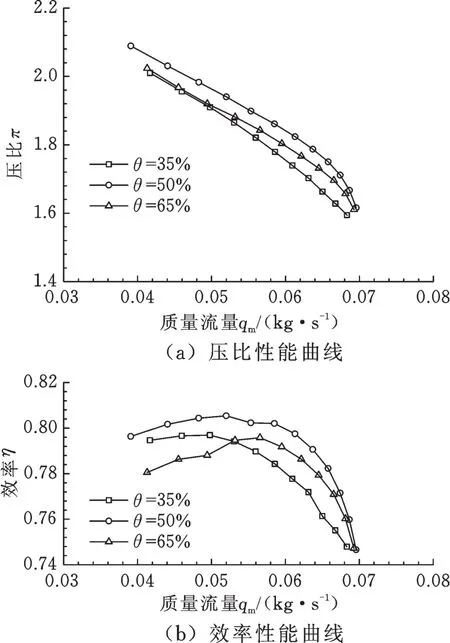
圖9 不同分流葉片周向位置對性能的影響Fig.9 In fluence of circum ferential position of different sp litter b lades on perform ance

3 相關性分析

將葉輪結構幾何參數都考慮進來作為設計變量進行優化計算，會造成樣本空間的數量過大。因此，需要依據參數對壓氣機性能影響程度大小的不同，篩選保留對性能影響程度較大的參數，將影響程度較小的變量則予以剔除，以此來降低樣本點的規模。假設某結構參數為變量X，某一氣動性能指標為變量Y，兩者之間的協方差：

cov(X,Y)=E(X-E(X))(Y-E(Y)) （1）

變量X和Y的相關系數為

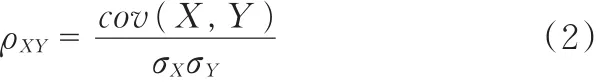
相關系數的大小意味著相關性的強烈程度，正負值則對應著是否為正負相關。通過求解變量與響應之間的協方差即可獲得各變量對響應的影響程度。

將各設計變量對響應值的相關系數進行絕對值加權平均處理，所得平均值的大小意味著該設計變量對目標值的影響程度的大小。采用拉丁超立方試驗設計方法在優化空間內產生樣本點，采樣規模為25，再對每個樣本點進行數值計算，得到其在設計流量和小流量下的壓比與效率。表2所示為各設計變量與響應值的相關系數值,可以看出，設計變量對壓比和效率的影響程度依次逐漸降低的順序為葉頂間隙t、葉片出口角β2b、葉片進口角β1b、包絡角δu、分流葉片周向位置θ、出口寬度b2。因此，選擇t、β2b、β1b、δu作為離心壓氣機葉輪多目標優化設計變量。

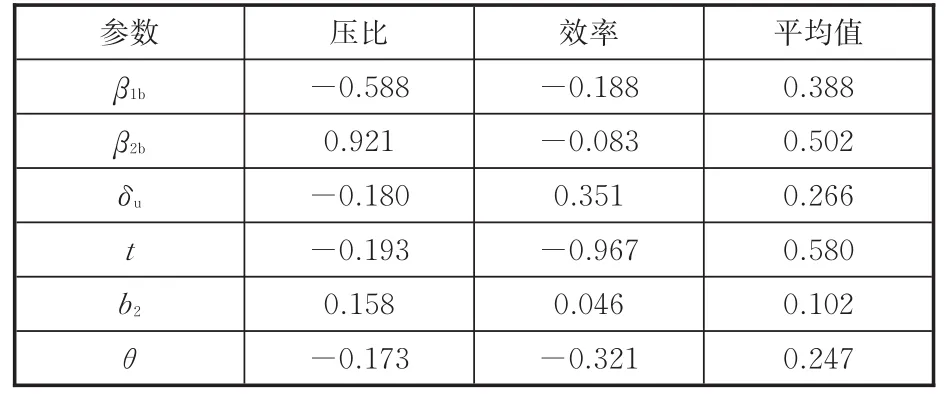
表2 設計變量與響應值的相關系數Tab.2 Correlation coefficients between designvariab les and response values

4 多目標優化

4.1 K riging模型

K riging模型由回歸模型和相關模型組成，有非常好的擬合精度。Kriging模型的數學描述形式如下：

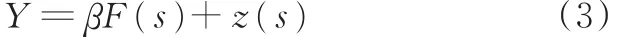
其中，F（s）為已知的回歸模型，通常采用多項式函數；β為相應的回歸系數，βF（s）形成對整個設計空間的擬合；z（s）為相關函數，用來表示設計空間在局部偏差上的近似。z（si）和 z（sj）之間的協方差為

式中，R為相關系數的矩陣。

元素 r（si，sj）是兩個不同樣本點 si、sj之間的距離函數，用來表示不同變量之間的空間相關性，其高斯函數形式為

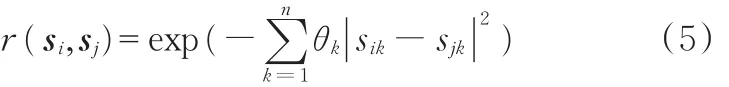
其中，n為設計變量中元素個數；θk為待定相關系數，可用來表示空間兩個不同樣本之間的相關性；sik和 sjk分別表示 si、sj在在 k方向上的分量。

根據相關性分析選取 t、β2b、β1b、δu為優化變量，以在設計流量和80%設計流量的小流量工況下的效率、壓比為目標進行拉丁超立方試驗，試驗安排如表3所示。

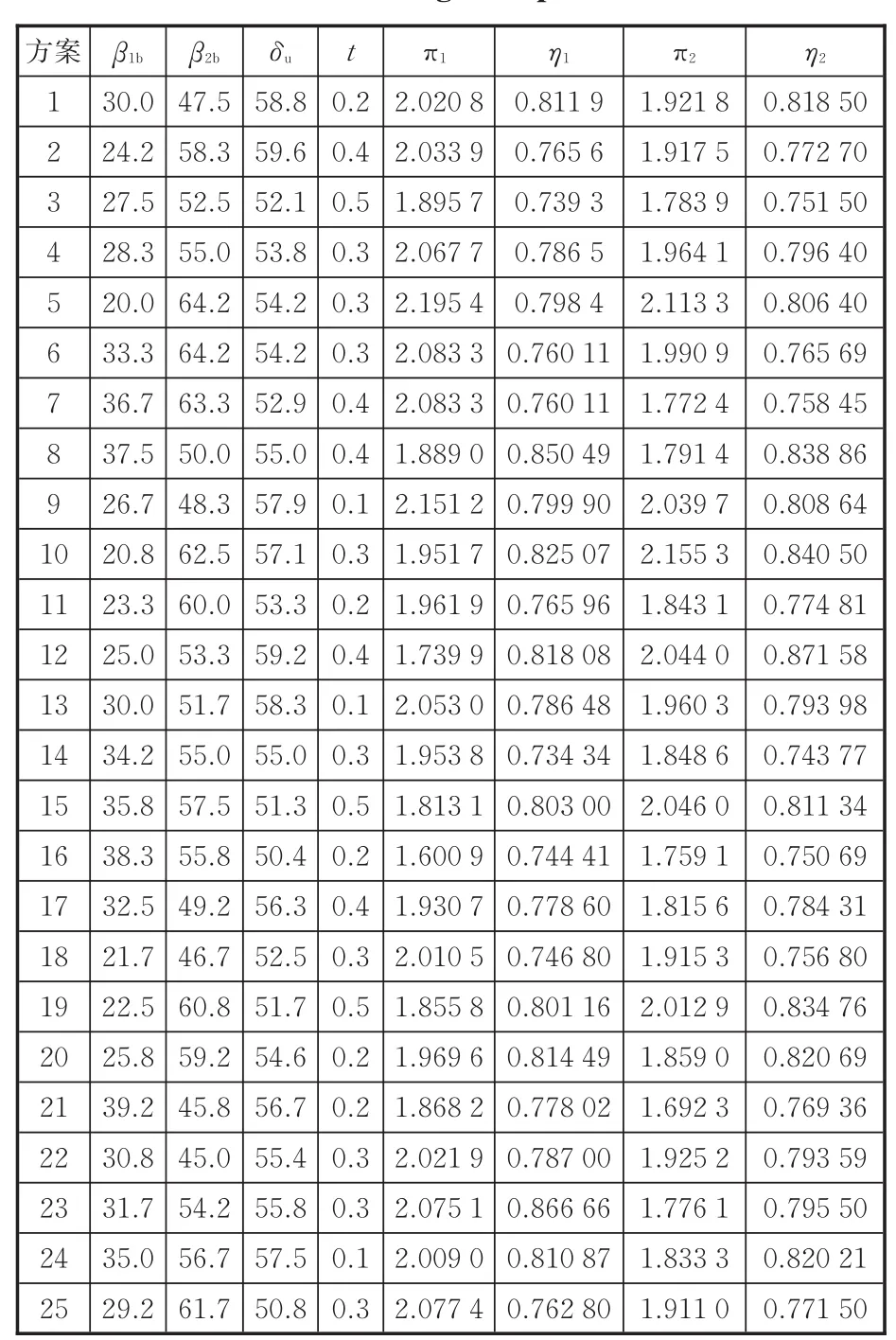
表3 葉輪拉丁超立方優化變量與目標響應值Tab.3 Im peller Latin hypercube op tim ization variables and target response values

根據表3葉輪優化變量與目標響應值樣本數據庫構建K riging模型，并另外選取15個測試樣本點對其進行驗證，采用R2誤差分析方法對近似模型的精度進行評估，其中R2取值范圍是［0,1］。R2的值越靠近1，擬合精度越好。計算所得壓比和效率的R2值分別為0.942 2、0.963 9，表明預測值和計算值吻合程度較好，可信度高，所建立的壓氣機Kriging模型滿足精度要求。

4.2 優化數學模型與求解

優化目標為設計流量下和小流量下的綜合效率和壓比，以t、β2b、β1b、δu為優化變量，以多工況加權平均效率ηave和壓比πave最高為目標建立優化數學模型：

ηave=0.8η1+ η2πave=0.8π1+ π2

通過NSGA?Ⅱ算法對優化模型進行尋優求解。設定初始種群為160，遺傳代數為200，交叉概率為0.95，變異概率為0.15。為進一步提高優化結果的精度，將求得的最優點進行流場分析，再將流場分析結果加入初始試驗樣本數據庫中，然后重新建立新的K riging近似模型，如此循環尋優，直到前后兩次優化點相差很小或者迭代數達到預先設定的值計算結束。所采用的優化流程如圖10所示。

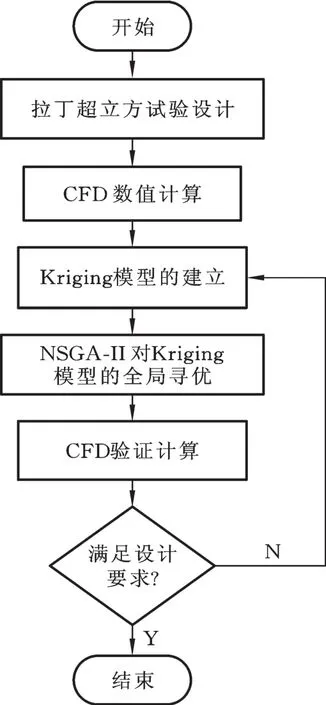
圖10 多目標優化流程圖Fig.10 Flow chart ofm ulti”objective optim ization

5 優化結果與討論

5.1 葉片結構對比

通過NSGA?Ⅱ尋優求解，得到壓氣機葉輪多目標優化Pareto最優解集前沿，選取一個效率和壓比都相對較高的折中解。表4給出優化前后葉輪結構參數。

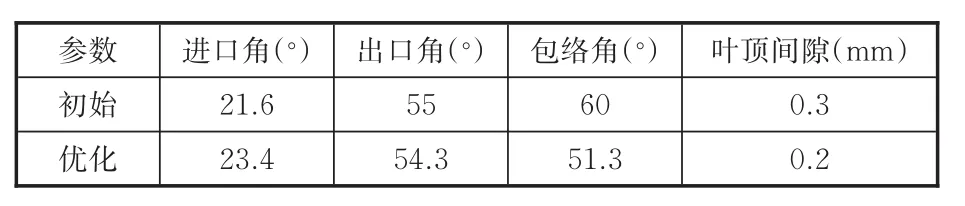
表4 優化前后的結構參數Tab.4 Structural parameters before and after op tim ization

由表4可以看到，優化后葉輪葉片包絡角較初始葉輪的葉片包絡角減小，由60°減小到51.3°，葉頂間隙由0.3 mm減小到0.2 mm，葉片進口角由21.6°增加到23.4°，葉片出口角由55°減小到54.3°。

5.2 總體性能比較

為對比優化前后葉輪性能，在同一轉速下，對優化后葉輪和初始葉輪分別進行多工況數值計算。圖11為優化葉輪和初始葉輪的總體性能曲線。

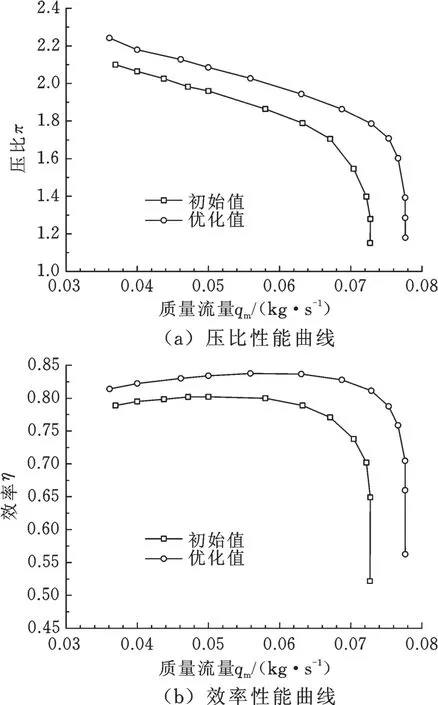
圖11 優化前后葉輪性能曲線對比Fig.11 Com parison of im peller performance curves before and after op tim ization

由圖11可見，優化后葉片在整個變流量工況范圍內效率和壓比都有所提高，特性曲線向右上方移動，變工況整體性能得到改善。同時，喘振點減少，阻塞流量堵塞點增加，即擴寬了穩定工作范圍。對優化后葉輪在設計流量工況下和小流量工況下進行數值計算，優化結果如表5所示。

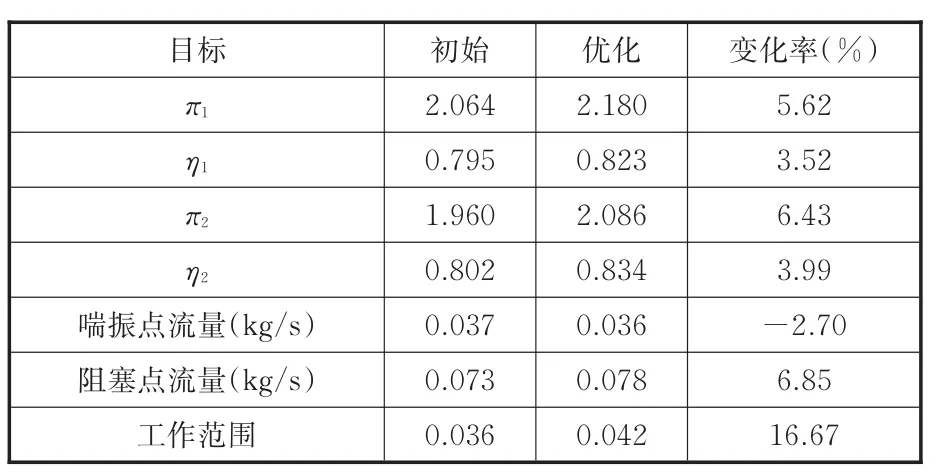
表5 優化設計點結果對比Tab.5 Com parison of resu lt on op timum design point

由表5可知，優化葉輪在設計點的壓比、效率和質量流量比初始葉輪都有增加。優化后，葉輪在設計流量點壓比提高了6.43%，效率提高了3.99%；在小流量點壓比提高了5.62%，效率提高了3.52%，優化葉輪喘振點流量相較于優化前減小了2.7%，而阻塞點流量增加了6.85%，工作范圍拓寬了16.67%。

5.3 內部流場對比分析

為進一步探索氣動性能變化的內在原因和葉輪三維流動本質，對壓氣機葉輪在設計流量點優化前后內部流場作了詳細對比分析。

圖12所示為優化前后設計流量下葉輪子午面上的熵增分布。由圖12可見，在靠近輪蓋側的位置，有熵增值顯著增大的區域，即代表葉輪中有流動損失的存在，其中優化前的葉輪高熵值所占據的范圍要大，峰值更高，而優化后高熵值減小，降低了流動損失。

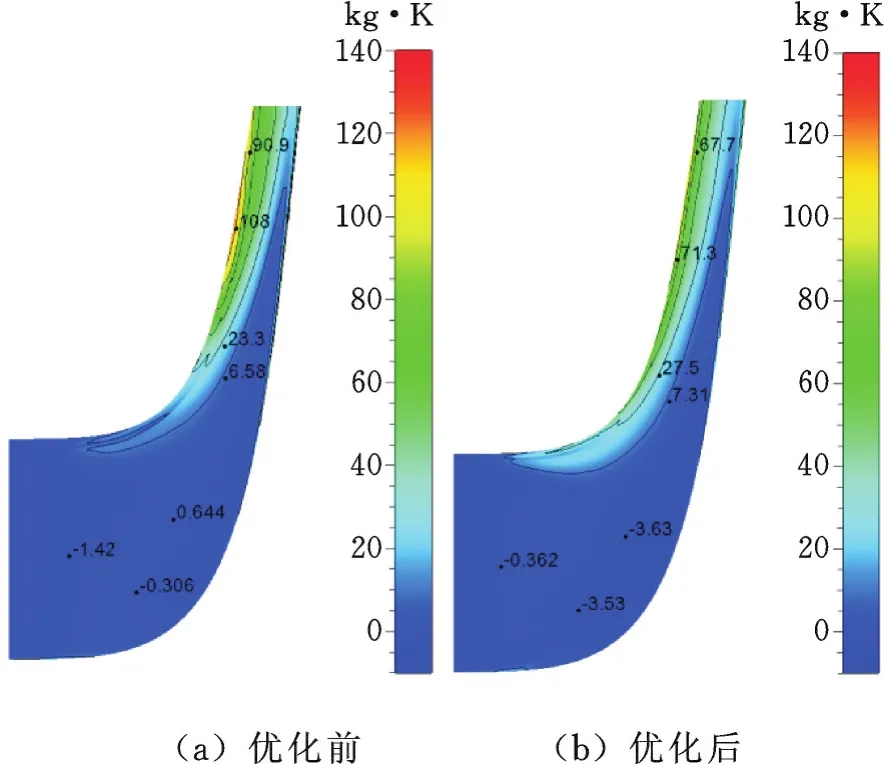
圖12 設計流量下優化前后子午面熵增分布Fig.12 The surface entropy distribution before and after optim ization of radial design flow

圖13所示為優化前后小流量下葉輪子午面上的熵增分布，可以看出，靠近輪蓋處熵增明顯增大，優化后該區域面積減小，同時峰值也降低，使得流動損失減少，流動情況變得均勻。

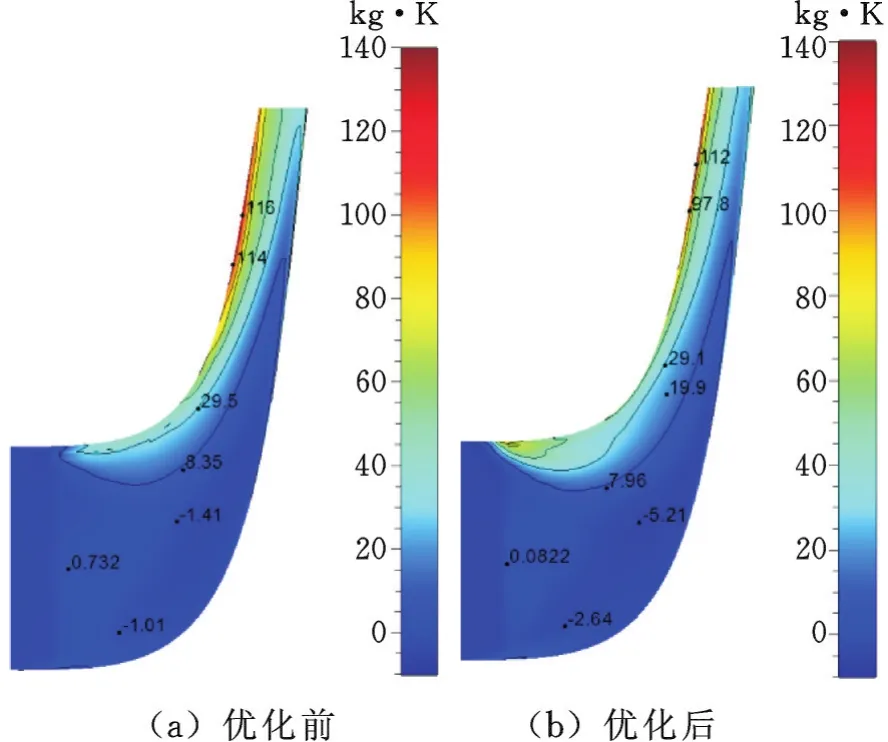
圖13 小流量下優化前后子午面熵增分布Fig.13 The sur face en tropy d istribu tion before and after op tim ization ofm erid ian under sm all flow

圖14給出了優化前后設計流量下出口馬赫數分布，可以看出，優化前，在葉輪通道內靠近輪蓋出現低速區域，形成低能流體匯聚區域并形成回流；靠近輪盤的地方有相對馬赫數高速區，形成射流流動結構。優化后，葉輪出口速度整體上進一步降低，回流現象和射流流動情況減弱。整個截面的相對馬赫數梯度減小，出口速度分布更加均勻。

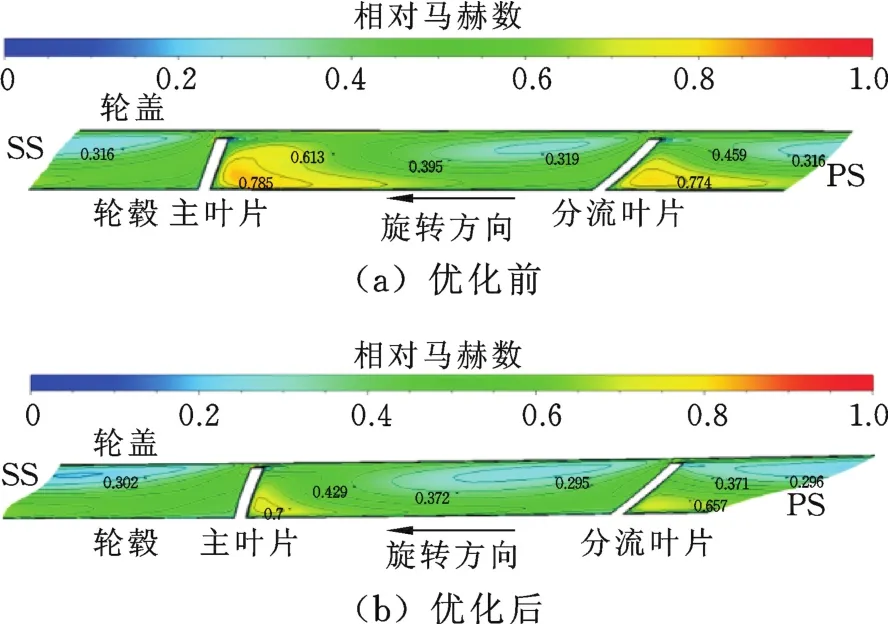
圖14 設計流量下優化前后出口馬赫數分布Fig.14 Distribu tion of M aher num ber at ou tlet before and after op tim ization

圖15所示為優化前后小流量下出口馬赫數分布，可以看出，優化后葉輪通道形成的回流和射流結構與優化前相比有所減弱。整個截面的相對馬赫數梯度減小，出口速度分布更加均勻，出口處的流動在小流量工況同樣得到改善。

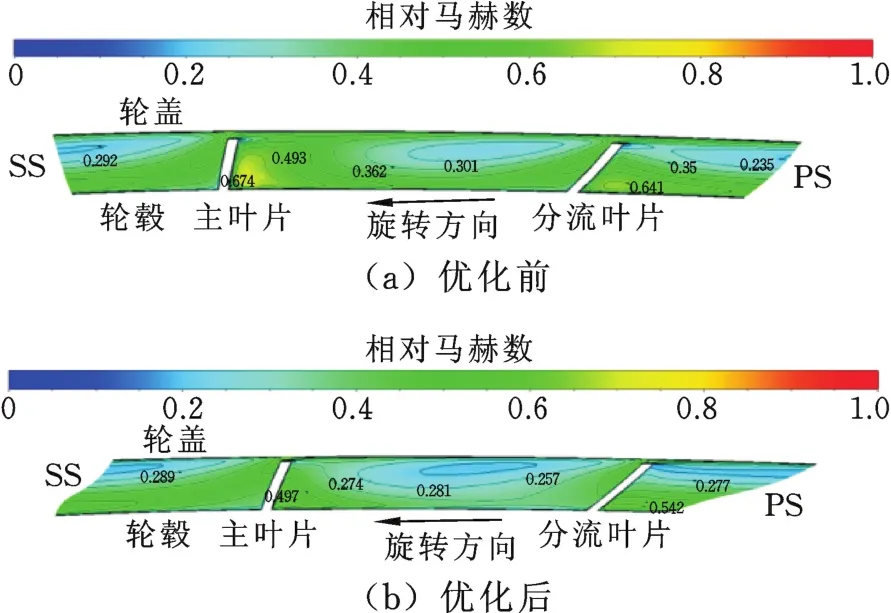
圖15 小流量下優化前后出口馬赫數分布Fig.15 Distribu tion of M aher num ber at ou tlet before and after op tim ization at sm all flow rate

6 結論

（1）本文探討了一種采用數值計算、拉丁超立方試驗設計和K riging代理模型相結合的離心壓氣機葉輪優化設計策略。

（2）基于三維黏性RANS流場分析，研究了離心壓氣機葉片進口角、葉片出口角、葉頂間隙、包絡角、分流葉片周向位置和出口寬度等幾何參數對性能的影響及相關程度。結果表明，對氣動性能影響程度依次逐漸降低的順序為葉頂間隙、出口葉片角、進口葉片角、包角、分流葉片周向位置和出口寬度。

（3）基于相關性分析建立降階的優化設計變量空間和多目標優化數學模型，應用NSGA-Ⅱ優化算法進行離心壓氣機葉輪Pareto多目標尋優。結果表明，優化葉輪小流量工況壓比增加了5.62%，效率增加了3.52%；設計流量工況壓比增加了6.43%，效率增加了3.99%，內部流場更均勻，流動損失減少；優化后全流量工況范圍內效率和壓比均有提升，喘振點流量減小2.7%，阻塞點流量增大了6.85%，擴大了壓氣機穩定工作范圍。