非周期信號作用下非線性動力系統的響應


摘 要:采用攝動法和卷積積分法,求解在周期信號作用下非線性動力系統響應的一階近似解.針對常見的幾個非周期激勵信號給出其卷積表達式,并對Duffing方程求解,得到令人滿意的效果.
關鍵詞:非周期信號;非線性;動力系統;Duffing方程
[中圖分類號]O302 [文獻標志碼]A
文章編號:1003-6180(2018)02-0030-04
Abstract:In this paper, by using the perturbation method and the convolution integral, we obtain the approximate first-order solution of nonlinear dynamic systems with non-periodic excitation and give the convolution expression for several common non-periodic excitations. Then the Duffing equation is solved by this method, and the obtained results are well agreed with the numerical results.
Key words:non-periodic excitation; nonlinear; dynamic systems;duffing equation
非線性動力學是研究非線性動力系統的運動模式和演化過程的科學,是現代科學技術的重要理論基礎.經過100多年的發展,非線性動力學已經取得大量的成果,發現了許多非線性現象,提出并發展了基本理論方法.[1-5]非周期信號作用下非線性動力系統的響應不但是一個重要的理論問題,而且在工程實際中具有重要的應用,遺憾的是,一直沒有求解該問題的解析方法,因此該問題的研究已成為當務之急.
非周期信號是科學研究及工程實際中經常遇到的信號,典型的非周期信號激勵有單位脈沖激勵、階躍信號激勵、矩形信號激勵等.通常情況下,系統所受的沖擊信號激勵可以等效成上述所提的非周期信號激勵.[6-7]沖擊是指一個系統在瞬間受到外載荷作用, 從而引起系統的位移、速度、加速度等系統物理量的突然變化,并且在一個相當小的空間內釋放出相當大的能量,從而會對結構、性能以及機械設備帶來一定的損傷和破壞,故需要研究動力系統受到沖擊作用的效果, 估計沖擊對系統結構的損傷及其耐沖擊能力.目前沖擊響應的解析研究均集中在線性系統,Laplace變換法或卷積積分法通常被用來計算線性系統的沖擊響應.對于非線性系統來講,上述方法不能直接解決沖擊響應的問題.在求解非線性動力系統的周期解時,攝動法是一種優秀的算法.本文采用攝動法和卷積積分法相結合,研究非線性動力系統的沖擊響應.
1 基于攝動法的非線性動力系統非周期信號激勵的響應
從圖5可以看出,采用攝動法和卷積積分相
結合的方法得到非周期激勵作用下的非線性動力系統的響應與數值解相比誤差較小,效果令人滿意,故可以采用該方法對非周期激勵作用下的非線性動力系統的響應求解.
4 結論
本文采用攝動法和卷積積分法相結合,對受非周期信號激勵的非線性動力系統求解,給出一階漸近解的表達式,針對常見的非周期激勵信號給出了具體的表達式.通過算例Duffing方程的求解,驗證結果令人滿意.
參考文獻
[1] 陳予恕. 非線性振動[M].天津:天津科技出版社,1983.1-8.
[2] 陳予恕.非線性振動系統的分岔和渾沌理論[M]. 北京: 高等教育出版社,1993.1-10.
[3] 胡海巖. 應用非線性動力學[M]. 北京. 航空工業出版社,2000.4-8.
[4] Yushu Chen and Andrew Y.T. Leung, Bifurcation and Chaos in Engineering [J]. New York: Springer, 1998. 1-5.
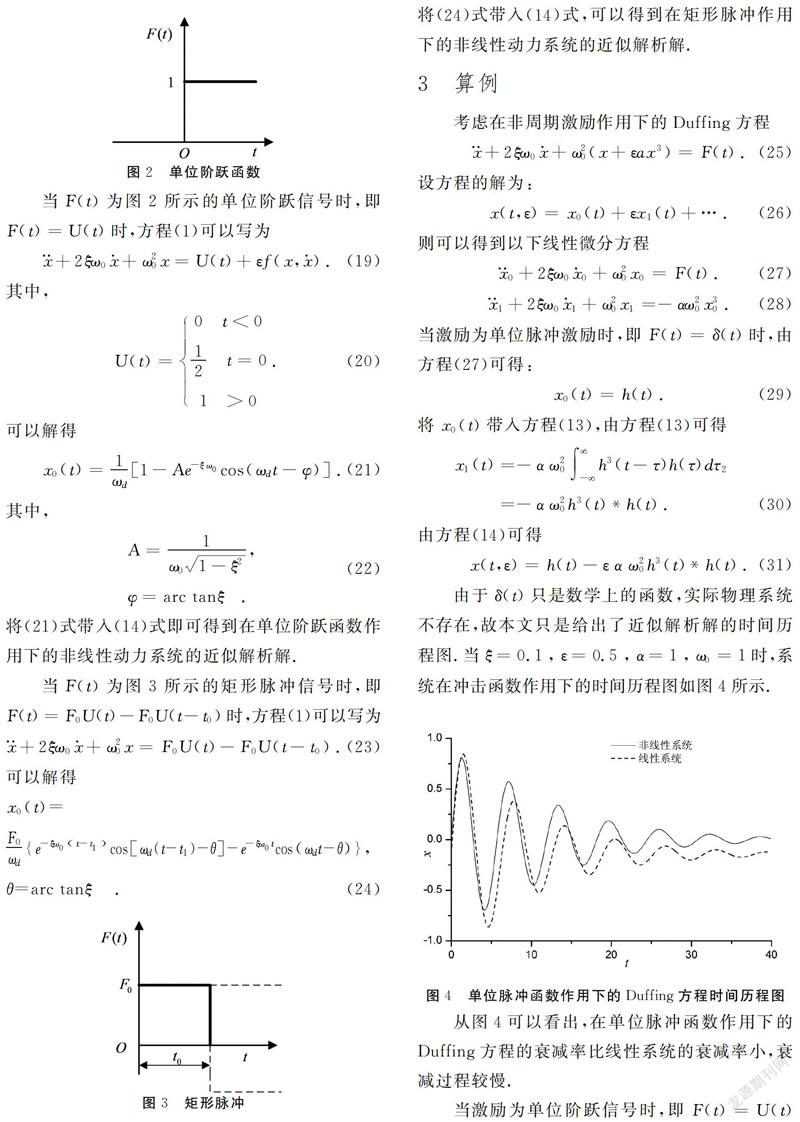
[5] Nayfeh. A. H. Nonlinear Oscillations [M]. New York: Wiley Interscience, 1979.1-10.
[6] 劉延柱, 陳文良,陳立群.振動力學[M]. 北京:高等教育出版社,1998.1-7.
[7] 劉延彬, 姜媛媛. 求解強非線性振動方程的加權余量遞推法[J]. 牡丹江師范學院學報:自然科學版, 2017(3):21-24.
編輯:琳莉

