蓄滯洪區社會穩定風險模糊層次墑權耦合分析

袁以美 陳建生

摘要：針對蓄滯洪區建設項目及其社會穩定風險因素的特點，建立評價指標體系和層次結構模型，應用模糊層次分析與熵權耦合的方法，在主觀賦權的基礎上增加能反映客觀要求的因素權重，并以蓄滯洪區為例進行應用研究，結果表明：雖然兩種不同方法產生的排在前3位的征地補償、移民安置、啟用后撤離與安置等社會風險因素沒有變化，但其綜合權重發生了變化，分別由0.3812、0.2147、0.2254變為0.4321、0.2734、0.1815;經耦合后啟用后撤離與安置權重變小，而征地補償、移民安置權重增大，主要風險因素權重增大，也說明前期工作的重要性;與單一方法相比，模糊層次分析與熵權法耦合應用于社會穩定風險分析，在一定程度上增強了分析結果的客觀性。

關鍵詞：蓄滯洪區;社會穩定風險;模糊層次分析;墑權

中圖分類號：TV873 文獻標志碼：A

開展建設項目社會穩定風險分析工作有利于促進科學決策、民主決策、依法決策，有利于獲得群眾對實施重大工程項目的理解與支持，有利于從源頭上預防和減少社會矛盾[1]。根據《水利水電工程可行性研究報告編制規程》（SL 618-2013），水利建設項目應在可行性研究階段進行社會穩定風險分析。產生社會穩定風險的根本原因是社會沖突，如果政策調整與利益分配不相適應，容易激化社會矛盾。再加上突發性群體性事件和不合適的社會輿論導向，很可能引發社會穩定風險[2]。若應對社會穩定風險不當，將會引發一系列社會問題[3]。社會穩定風險分析主要包括風險調查、風險因素分析、風險防范與化解措施和風險分析結論等[4]。風險因素分析是在風險調查、風險識別的基礎上，確定風險因素權重，從而進行風險估計，為制定風險防范和化解措施提供基礎。其中，確定風險因素權重是風險因素分析的重要內容。

風險因素權重的確定方法主要有故障樹法、德爾菲法、貝葉斯網絡法、蒙特卡洛仿真模擬法、層次分析法（AHP法）等。其中，層次分析法在故障樹法的基礎上，進一步利用了人們的知識和經驗，并將定性因素定量化，具有重要的理論意義和廣泛的應用價值[5]。近些年來，陸續出現了一些基于層次分析法的改進方法，如模糊層次分析法[6]、加速遺傳算法的層次分析法（AGA-AHP）、灰色層次分析法、熵權層次分析法[7]。本文在前人研究成果的基礎上，對層次分析法進行改進，提出模糊層次分析與熵權耦合法，并應用于某蓄滯洪區社會穩定風險因素分析中。

蓄滯洪區建設與一般的重大水利工程建設不同，蓄滯洪區運用概率較低，區內不可能全部移民。工程的建設既要做好一部分工程征地移民工作，還要考慮區域范圍內的村鎮經濟發展將由此受到限制、啟用蓄滯洪區后的區內群眾撤離及對群眾財產的淹沒賠償等問題[8]。在蓄滯洪區社會穩定風險因素分析中，為了在主觀賦權的基礎上反映客觀要求的權重，將模糊評判、層次分析法與熵權法相耦合，與單一的方法相比，評判結果更接近實際。

1 模糊層次分析與墑權耦合法

1.1 層次分析法

模糊層次分析法是將層次分析法與模糊綜合評價相結合的方法。層次分析法是指將一個復雜的多目標決策問題作為一個系統，將目標分解為多個目標或準則，進而分解為多指標的若干層次，通過定性指標模糊量化方法得出層次單排序和總排序，以此進行多方案優化決策的系統方法。其特點在于可為決策人提供多種決策方法，能夠有效解決很多難以完全用定量或定性方法解決的實際問題。但是，其局限性也很明顯，其基礎是專家的主觀判斷。層次分析法一般包括構造遞階層次結構、建立判斷矩陣A={a_ij}、層次單排序及一致性檢驗、層次總排序權重（W_j）及一致性檢驗。

1.2 模糊綜合評價[9]

模糊綜合評價的基本思想是：在確定評價因素、因子的評價等級和權值的基礎上，運用模糊集合變換原理，以隸屬度描述各因素、因子的模糊界線，構造模糊矩陣，通過多層復合運算，最終確定評價對象所屬等級。首先，建立模糊評價因素集，即由層次分析法識別的各風險因素的集合：

其次，建立風險評價集：

V={V₁，V₂，…，V_m}（2）

第三，進行單因素評判。根據已確定的評價等級標準，邀請相關行業專家對各個風險因素進行評價，可分別得出各子集B_i（i=1，2，…，m）中單要素的評價矩陣R_i，由B_i的權重系數向量W_i和評價矩陣R_i合成運算，得

第四，進行綜合評判。根據單因素層次分析法結果，得到U各子集的綜合評價矩陣R：

R=[Y₁，Y₂，…，Y_m]^T（4）

最后，由下式可得到最終模糊綜合評價結果：

Y=WR=[y₁，y₂，…，y_m]（5）式中：W為U的各子集對總目標的權重向量。

即可得到風險因素的整體評價。

1.3 熵權法

嫡是表示熱力學系統的無序或混亂程度，在信息論中用于度量數據所提供的有效信息量。熵權是在各種評價指標值確定的情況下，各指標在競爭意義上的相對激烈程度系數。當評價對象在某項評價指標上的值相差較大時，嫡值較小，說明該評價指標提供的有效信息量比較大，則該指標的權重也較大[10]。因此，熵權法賦權實際上是一種較為客觀的賦權方法。

按式（6）至式（8）歸一化處理判斷矩陣：

（極大型指標）

（極小型指標）

評價指標的信息嫡：

熵權可按下式計算：

1.4 耦合

根據u_j與模糊層次分析法得到的W_j，按下式進行耦合：

即可得到耦合后的綜合權重T_i。

2 工程實例

2.1 工程概況

某蓄滯洪區為北江中下游防洪工程體系的有機組成部分，區內的村莊依山傍水，堤圍外平坦開闊，堤圍內多為低丘平原，低丘平原區地勢低洼縱深小，歷史上就是天然的滯洪區，遇大洪水時居民可較快速地撤離到附近的山崗。當北江發生300a一遇洪水時，通過飛來峽水庫調度攔蓄13.07億m³洪量，水庫控泄16000m³/s，再經該蓄滯洪區滯蓄4.11億m³洪量，將北江中下游防洪控制斷面石角站的洪峰流量控制在18800m³/s（100a一遇）以下，確保廣州、佛山、清遠等珠三角重要城市的防洪安全。蓄滯洪區的堤防工程按20a一遇標準建設，區內建設內容包括建設安全區，新建、改建撤退道路，新建橋涵，購置搶險設施，建設蓄滯洪區通信預警系統等。根據規劃要求，蓄滯洪區內需要控制已有村鎮的發展規模及人口的增長，在條件許可的情況下，有計劃地逐步減少當地居民，同時限制永久性大中型工業項目的建設，交通、電力與通信等基礎設施的建設要充分考慮洪水風險，并滿足安全轉移及恢復生產的要求。當江口圩水位超過20.8m時，規劃蓄滯洪區范圍內的所有堤圍全部恢復天然滯洪作用。工程建成后，發生大洪水時，一旦啟用蓄滯洪區，區內居民必須臨時撤退，搬往安置區，洪水退后還要恢復生產，這必將凸顯利益付出者與受益者的矛盾[11]。此時是社會穩定風險的高發期。

2.2 指標體系建立及AHP權重

在風險識別的基礎上，篩選出與本項目密切相關的社會穩定風險因素，共3類10種，分為目標層（A）、準則層（B₁～B₃）和指標層（C₁～C₁₀）等3個層次（見圖1）。邀請社會評價專家和環境評價專業、征地專業、施工專業的專家共13人，采取1～9標度法對每個風險因素進行打分，確定本項目第i種因素風險的風險概率p_i、風險影響q_i及風險程度R_i。準則層B對于目標層A的判斷矩陣、單排序權重、一致性檢驗結果見表1，指標層C對于B₁～B₃的判斷矩陣、單排序權重、一致性檢驗見表2～表4，層次分析法各風險因素總排序權重見表5。

2.3 熵權法權重及綜合權重

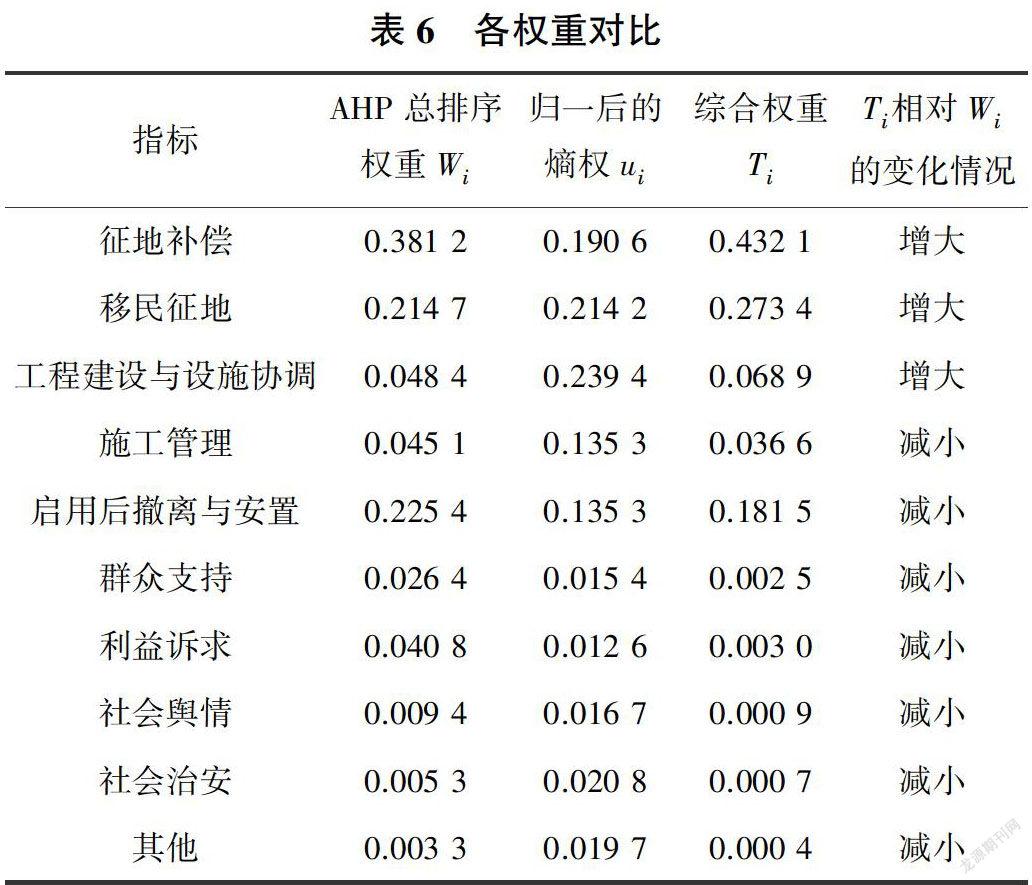
根據前述模糊層次分析法及熵權法耦合原理及公式，可得到AHP總排序權重W_i、歸一后的熵權u_i及耦合后的綜合權重T_i，見表6。

2.4 討論

（1）從AHP總排序權重W_i、礁、歸一后的熵權u_i及耦合后的綜合權重T_i來看，該工程社會風險因素排在前5位的均為征地補償、移民安置、工程建設與設施協調、施工管理、啟用后撤離與安置，這5個因素權重之和分別為91.48%、91.48%、99.25%，而群眾支持、利益訴求、社會輿情、社會治安及其他為相對次要的因素，這5個因素權重之和分別為8.52%、8.52%、0.75%。這與類似工程結論是一致的[12]。

（2）AHP總排序中，排在前3位的社會風險因素為征地補償、移民安置、啟用后撤離與安置，其權重分別為0.3812、0.2147、0.2254，占總權重的82.13%。模糊層次分析法及熵權法耦合后，主要因素仍然為征地補償、移民安置、啟用撤離與安置，但綜合權重發生了變化，分別為0.4321、0.2734、0.1815，占總權重的88.70%。相對AHP總排序，模糊層次分析法及熵權法耦合后的征地補償及移民安置權重有所增大，啟用后撤離與安置權重有所減小。

（3）考慮熵權法后，在主觀賦權的基礎上反映客觀要求的權重，主要風險因素權重增大。當前期工作做得充分時，后期啟用后撤離與安置風險權重減小，也意味著風險降低，這說明了前期工作的重要性。綜上所述，模糊層次分析法及熵權法耦合后的權重，比單純應用AHP法得到的權重更貼近工程實際，并體現了前期工作的重要性。

3 結論

在層次分析法的基礎上，將模糊層次分析與熵權法耦合應用于某蓄滯洪區社會穩定風險分析中，體現了在主觀賦權的基礎上反映客觀要求的權重。雖然排在前3位的社會風險因素沒有變化，但其綜合權重發生了變化。啟用后撤離與安置權重變小，而征地補償、移民安置權重增大，說明主要風險因素權重增大，也說明前期工作的重要性，當前期工作做得充分時，后期風險就會降低。這一結論更符合工程實際，與單一的方法相比，模糊層次分析與熵權法耦合應用于社會穩定風險分析，在一定程度上增強了分析結果的客觀性。

參考文獻：

[1]王水平，鄒洪，冷淑蓮，等.構建重大工程項目社會穩定風險評估機制的研究[J].價格月刊，2011（12）：1-14.

[2]李晶晶，華堅.重大水利工程項目社會穩定風險評估綜述[J].水利經濟，2016，34（7）：4-8.

[3]趙浩珠.水利水電工程建設征地與移民安置社會風險分析[J].低碳技術，2017（15）：37-38.

[4]袁以美，葉合欣，陳建生.某灌區節水改造工程社會穩定風險分析探討[J].人民珠江，2018，39（7）：79-83.

[5]金菊良，魏一鳴，付強，等.改進的層次分析法及其在自然災害風險識別中的應用[J].自然災害學報，2002，11（2）：2-5.

[6]王娟麗.基于AHP-FCE法的重大項目社會穩定風險評估[J].社會科學家，2017（2）：67-73.

[7]王清源，潘旭海.熵權法在重大危險源應急救援評估中的應用[J].南京工業大學學報（自然科學版），2011，33（5）：87一92.

[8]林韜.潖江蓄滯洪區建設運行與社會穩定風險問題研究[J].廣東水利水電，2017（1）：15-17.

[9]歐陽靖雯，王月明，張現樂，等.基于AHP-模糊綜合評價的風險分析及MATLAB應用[J].四川建筑，2012，32（2）：280-283.

[10]倪九派，李萍，魏朝富.基于AHP和熵權法賦權的區域土地開發整理潛力評價[J].農業工程學報，2009，25（5）：204-208.

[11]張彬，余文學.利益均衡下的蓄滯洪區運用機制構建[J].人民黃河，2010，32（3）：6-8.

[12]廣東省水利電力勘測設計研究院.潖江蓄滯洪區建設與管理工程可行性研究報告[R].廣州：廣東省水利電力勘測設計研究院，2016：16-28.