高中理科數學概率應用題解題技巧談

馮國棟

（四川省西充中學，四川 南充）

縱觀歷年高考試卷，不難發(fā)現：一直以來，概率應用題始終是高考數學的必考點。然而，部分學生因為沒有熟練掌握概率應用題的解題技巧，所以在解答概率應用題的過程中老是愛出錯，總是在丟分。

基于此，廣大高中數學教師在堅持不懈地探究一些高中理科數學概率應用題的解題技巧，旨在提升高中學生解答概率應用題的速度與效率。雖然廣大教師對于高中理科數學概率應用題的解題技巧關注熱度未曾衰減，但是對于這方面的研究卻未曾深入，以至于現階段有關高中理科數學概率應用題解題技巧的理論研究成果為數不多。下面筆者將在理論聯系實際的基礎上，淺顯論述一些高中理科數學概率應用題的解題技巧，希望本研究能夠起到拋磚引玉的作用，能夠吸引更多的高中教師研究高中理科數學概率應用題解題技巧。

一、公式法——讓概率應用題有章可循

公式法是解答高中理科數學概率應用題的基本方法之一。學生要想準確無誤地運用公式法解答高中理科數學概率應用題，首先必須要全面透徹地理解這些與概率相關的公式。唯有如此，學生才能在解答概率應用題的過程中，快速準確、靈活自如地運用這些公式。

有鑒于此，在高三數學教學過程中，教師要引領學生聚焦各種與概率問題相關的公式，不僅要讓學生重溫這些概率公式，還要讓學生對這些概率公式有更進一步的理解。如此這般，學生運用這些公式解決高中理科數學概率應用題的能力才能夠得到顯著提升。

比如說，“全概率公式”是高中階段學習的一個重要的概率公式。該公式的具體內容是已如某事件A是有B，C，D三種因素造成的，求這一事件發(fā)生的概率，用字母表示為：p（A）=p（A/B）p（B）+p（A/C）p（C）+p（A/D）p（D）。在高三復習階段，教師通過引領學生重溫這一公式，能夠切實提升學生運用這一公式解答概率應用題的能力。

由此可見，公式法能夠讓高中學生在解答概率應用題的時候有章可循。或者說，公式法能夠為高中學生解答概率應用題指出明確的方向。

二、樹狀圖法——讓概率應用題層次分明

樹狀圖法，顧名思義，就是通過讓學生繪制一種類似于樹的形狀的圖案來解答概率應用題的一種方法。因為樹狀圖法圖文并茂，所以樹狀圖法能夠讓解題者全腦工作，即讓解題者左右腦同時聚焦到題目內容上來。這樣一來，學生解答題目的速度與準確度自然也會得到大幅提升。

因此，在高中理科數學教學過程中，教師可以指導學生運用樹狀圖法解答一些概率應用題。樹狀圖法能夠讓抽象的高中理科數學概率應用題層次分明。據此，高中學生解答概率應用題的能力也會得到明顯提升。

例題：經過某十字路口的汽車，它可能繼續(xù)直行，也可能向左轉或向右轉，如果這三種可能性大小相同。三輛汽車經過這個十字路口，求下列事件的概率：（1）三輛車全部繼續(xù)直行；（2）兩輛車向右轉，一輛車向左轉；（3）至少有兩輛車向左傳。

在解答這道概率應用題的時候，學生就可以利用樹狀圖。樹狀圖下圖所示：

解：畫樹狀圖如下：

樹狀圖法能夠充分發(fā)揮學生形象思維能力與抽象思維能力，能夠極大地提升學生解答高中理科數學概率應用題的能力。

三、面積法——讓概率應用題一目了然

在解答高中理科數學概率應用題的時候，如果學生能夠將抽象的題目內容形象化、直觀化，那么，學生解答題目的難度就會明顯降低許多。為了能夠將抽象的題目形象化、直觀化，教師可以指導學生巧妙地利用面積法快速準確地解答高中理科數學概率應用題。

面積法，簡而言之，就是讓學生以圓面積圖示的形式將高中理科數學概率應用題的內容形象逼真的展現出來。如此一來，概率應用題的內容就會一目了然。

例題：在正方形中隨機撒一把豆子，用隨機模擬的方法估計圓周率的值。（假設正方形的邊長為2）。

在解答這道概率應用題的時候，教師就可以指導學生運用面積法。如圖所示：

解題步驟如下：

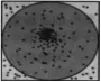
由此可見，學生運用面積法能夠更加透徹理解概率應用題的主旨。在此基礎上，學生就能夠快速準確地解答概率應用題。

綜上所述，為了切實提升高三學生解答概率應用題的能力，教師要讓學生在透徹理解一些概率公式的前提下，靈活自如地運用這些公式解答概率應用題；教師要讓學生在準確理解概率應用題題目意思的前提下，恰如其分地運用樹狀圖法解答概率應用題；教師要讓學生在整體把握概率應用題題目主旨的前提下，形象逼真地運用面積法解答概率應用題。

總而言之，教師要緊扣概率應用題題目內容，全方位、多角度引領學生探究解答概率應用題的技巧，借此提升學生解答概率應用題的能力。