面向神經網絡加速器的近似加法器的電路設計

吳成均 單偉偉

摘要：近似計算單元以一定的計算誤差換取更低功耗，近年來在神經網絡加速器中得到應用。本文通過研究不同近似加法器的誤差特性、在典型神經網絡應用中的結果以及功耗節省情況，對神經網絡加速器進行最優近似設計。首先利用MATLAB對近似加法器建立數學模型，分析平均誤差距離等誤差特性，用HSPICE設計電路進行功耗仿真，為近似加法器在神經網絡上的應用提供指導原則。用Python搭建多層感知機和卷積神經網絡，設計兩層結構的近似加法器算法模型，替換網絡中的精確加法器，研究不同誤差特性、不同近似位寬的加法器對神經網絡各個指標的影響。研究表明，平均誤差小的近似加法器對輸出質量影響小，且近似位寬存在閾值，超過閾值會導致輸出質量驟降，同時近似加法器能大幅降低計算功耗，而通過提出的輸出質量一功耗收益可以找到整體收益最高的設計。本文提出的方法能高效系統地為神經網絡加速器進行最優的近似設計。

關鍵詞：近似計算;神經網絡;近似位寬;低功耗;整體收益

中圖分類號：TN49 文獻標識碼：A

近似計算技術是一種新興的高能效設計技術，其計算過程并非完全正確，但由于采用精簡計算邏輯，簡化了計算過程，大大減少了系統的計算功耗，可以在電路[1，2]、架構[3]、算法[4]三個層面上實現，電路級別主要是近似計算單元的設計。近似計算適合具有容錯性[5]的應用，容錯性是指應用計算過程中出現的一些錯誤不會對最終輸出結果產生嚴重影響。人工神經網絡是典型的容錯性應用之一，它的容錯性主要來源于兩個方面：一個是分層分布式結構使其具有弱化計算錯誤對輸出質量影響程度的能力，另一個是特有的訓練過程可以減少實際輸出和理想輸出的誤差。而人工神經網絡作為人工智能的主流實現算法正在蓬勃發展，基于其特殊的計算模式，相比于CPU或者GPU，利用專用的神經網絡加速器[6]進行計算是一種更高效的設計，神經網絡加速器主要由乘加計算單元構成，大量的乘加計算會產生很高的功耗。隨著人工智能向移動化發展，考慮到電池供電的特性，神經網絡加速器的低功耗設計成為一大需求。結合近似計算和神經網絡的特性以及需求，將近似計算技術加人神經網絡加速器中具有很好的應用前景。

已有的研究[7，8]通常在算法層面上將近似計算技術加入到簡單神經網絡，而缺乏在電路級別將近似計算單元加人神經網絡加速器的設計。本文研究了近似計算單元對神經網絡輸出質量和功耗的影響，為其應用提供指導原則，提出了一套完整的設計方法，可以在電路級別為神經網絡加速器進行最優的近似設計，在降低輸出質量損失的同時，盡可能地降低系統計算功耗。

1 近似加法器及誤差衡量指標

神經網絡加速器中最基本的計算單元是加法器，因此近似計算單元的設計往往是近似加法器和近似乘法器的設計。

1.1 精確加法器

精確1-bit加法器實現兩操作數相加，邏輯表達式如下：

最基本的全加器電路結構是按照式（1）和式（2）由兩個異或門、兩個與門和一個或門構成，本文以上述經典結構來實現精確加法器，為近似加法器提供對比基準。

1.2 近似鏡像加法器

近似鏡像加法器（AMA）[9]是在鏡像加法器（MA）的基礎上設計的，相比傳統CMOS電路的對偶結構，MA的鏡像結構可以保證移除部分晶體管時不會出現電源到地短路或輸出斷路的情況。通過移除部分計算電路的晶體管，得到三種近似鏡像加法器（AMA1、AMA2、AMA3），如圖1所示，極大降低了計算功耗。

1.3 低位或加法器（LOA）

低位或加法器（LOA）[7]將一個P位的加法器拆分成兩個分別為m位和n位的小加法器（p=m+n），其中m位的小加法器由精確加法器構成，而n位的小加法器由或門構成，實現兩個操作數低n位的近似相加，如圖2所示。由于舍棄了低位部分的進位鏈，LOA在功耗、延遲和面積方面都有不錯的表現。

1.4 低位忽略加法器（LIA）

低位忽略加法器（LIA）并不是一種具體的近似計算單元，而是對減少位寬這種近似方法的一個抽象，將低位直接截斷后，只進行高位的加法運算，可以理解成輸出恒為0的近似加法器，用其來實現低位部分的相加，通過這種抽象，可以使減少位寬的近似方法與近似加法器有統一的描述，以便后面作為衡量近似加法器的一個基準。

1.5 誤差衡量指標

各個近似加法器差別很大，本文使用以下幾個指標綜合衡量其誤差特性：

（1）誤差率

誤差率指近似計算單元錯誤輸出占總輸出的比例，可以反應近似計算單元出錯的頻率。

（2）平均誤差距離

誤差距離[10]指近似輸出與精確輸出的差值，大量輸入下的平均效應能更好地反應近似加法器的誤差累積效應，平均誤差距離越大，誤差累積越嚴重，對輸出質量影響越大。近似計算單元的所有輸入具有隨機性，可以認為呈現均勻分布，因此對所有輸入下的誤差距離求均值即可獲得平均誤差距離。

（3）最大誤差距離

最大誤差距離指近似加法器在單次計算中可能出現的最大誤差，反應最大的誤差嚴重程度，最大誤差距離越大，越容易對應用的結果產生嚴重影響。

2 近似加法器的誤差特性分析

本文利用MATLAB建立誤差模型，從多個指標綜合分析誤差特性，為近似加法器在神經網絡中的應用提供指導原則。

多位近似加法器在實際應用中通常分成高位精確部分和低位近似部分，通過建立一個模型框架，高位采用精確加法器，低位替換成各種近似加法器，即可實現模型復用，將5種近似加法器LIA、LOA、AMA1、AMA2、AMA3的真值表導入框架，設定多位加法器的總位寬N為8位，近似位寬k分別設定為1～8位，讓模型遍歷所有可能的輸入，以精確加法器輸出為基準，統計各種誤差指標，如圖3所示，橫坐標是近似部分位寬，縱坐標分別是誤差率、平均誤差距離、最大誤

仿真結果表明，隨著近似位寬的增大，5種近似加法器的誤差率都不斷增大，LOA誤差率最低，而LIA的誤差率最高。LOA和AMA3的平均誤差距離最小并且基本不隨近似位寬而變化，不會產生嚴重的誤差累積，而LIA和AMA2的平均誤差距離的絕對值比較大，并且隨著近似位寬的增大誤差累積越來越嚴重。此外，LIA的最大誤差距離明顯大于其余4種近似加法器，表明LIA在實際應用中很容易對計算結果產生嚴重影響，而LOA和AMA3的最大誤差距離是最小的。

綜合以上指標，理論上，在將近似加法器加人到神經網絡時，LOA和AMA3對網絡的影響是最小的，而傳統減少位寬的方法影響是最大的。

3 近似加法器的日SPICE仿真及功耗特性分析

本文利用HSPICE，使用SMIC40nm工藝的單元庫設計各加法器，采用TT工藝角，在電源電壓1.1V和測試溫度25℃的條件下，對幾種近似加法器和精確加法器進行功耗仿真，由于靜態功耗相比動態功耗非常小，本文只考慮動態功耗。輸入包含64種狀態轉變情況的激勵波形，通過瞬態分析獲得如圖4所示的功耗跡曲線。

仿真結果表明，加法器在不同狀態轉變時產生的功耗差別很大，不同加法器的功耗跡形狀也不同。對64種狀態轉變下的功耗求平均值，用平均功耗來表征加法器的功耗水平。可以看出，近似加法器的平均功耗均明顯低于精確加法器，LOA和AMA3相比于精確加法器減少了約85%的功耗。

4 近似加法器在神經網絡中的應用

4.1 近似神經網絡的搭建

在Python環境下搭建了5層的多層感知機MLP-5和8層的卷積神經網絡CNN-8，如圖5所示。網絡中每一層的神經元數量可以通過參數設定，激活函數可以選擇為tanh函數或者sigmoid函數，網絡具有很大的靈活性，可以適配不同的應用。MLP-5網絡結構簡單，采用全連接結構，分類IRIS數據集，而CNN-8包含卷積層、池化層和全連接層，相對復雜，分類MNIST數據集。采用12位定點數數據格式訓練網絡，MLP-5和CNN-8分別達到97.78%和96.7%的分類準確率。兩種網絡的乘加計算量見表1。

為了研究近似加法器對神經網絡輸出質量和功耗的影響，需要將網絡中的精確加法器替換成近似加法器，而傳統框架（如TensorFlow）很難單獨對加法運算進行修改，設計效率低，而本文搭建的網絡靈活性很大，每一個神經元的加法器以及位寬都可以單獨修改，非常適合搭建近似神經網絡。

根據每種近似加法器的真值表編寫對應的近似加法函數，并且編寫了兩層結構的多位加法函數，高位部分采用精確加法函數，低位部分采用近似加法器對應的近似加法函數，總位寬為12位，低位近似部分的位寬可以修改，如圖6所示，最后在MLP-5和CNN-8的基礎上，利用多位近似加法函數替換多位精確加法函數，搭建近似神經網絡。而通過替換近似加法函數、修改近似位寬，可以研究不同誤差特性和不同近似位寬的加法器對神經網絡的影響。

在圖6中，m為近似位寬，而m-bit的近似加法器可以由LIA、LOA、AMAl、AMA2、AMA3的任意一種構成。

4.2 衡量指標

本文從輸出質量、歸一化功耗、整體收益三個指標來綜合衡量近似加法器對神經網絡的影響。

（1）輸出質量

輸出質量具體指MLP-5和CNN-8對相應數據集的分類準確率。

（2）歸一化功耗

神經網絡的功耗通常指執行階段的功耗，即執行單次分類任務產生的功耗，又可分解為參數訪存功耗和計算功耗。計算功耗與操作次數以及單次操作功耗有關，神經網絡中涉及到的計算包括加法運算、乘法運算和非線性激活函數的運算。由于本文只修改了MLP-5和CNN-8網絡中的加法器，后續的功耗分析都是針對加法計算功耗。根據上面功耗分析的結果，可以估算得到加法計算功耗E_APPRO，并且除以精確網絡的加法計算功耗E_ACC，得到各個近似神經網路的歸一化加法計算功耗NE。

（3）輸出質量一功耗收益

本文提出了輸出質量一功耗收益的概念來綜合評估近似加法器的影響，對于一個近似神經網絡，其輸出質量一功耗收益定義為：式中：E_SAVE為功耗的節省值，Q_LOSS為輸出質量的損失值，w₁和w₂為權重，根據不同應用對輸出質量和功耗的要求，可以設置不同的權重，輸出質量一功耗收益數值越大，表示整體收益越高。本文w₁和w₂都設置為1，指每單位輸出質量損失下功耗的節省值。通過輸出質量一功耗收益指標，可以為應用找到收益最高的設計。

4.3 試驗結果

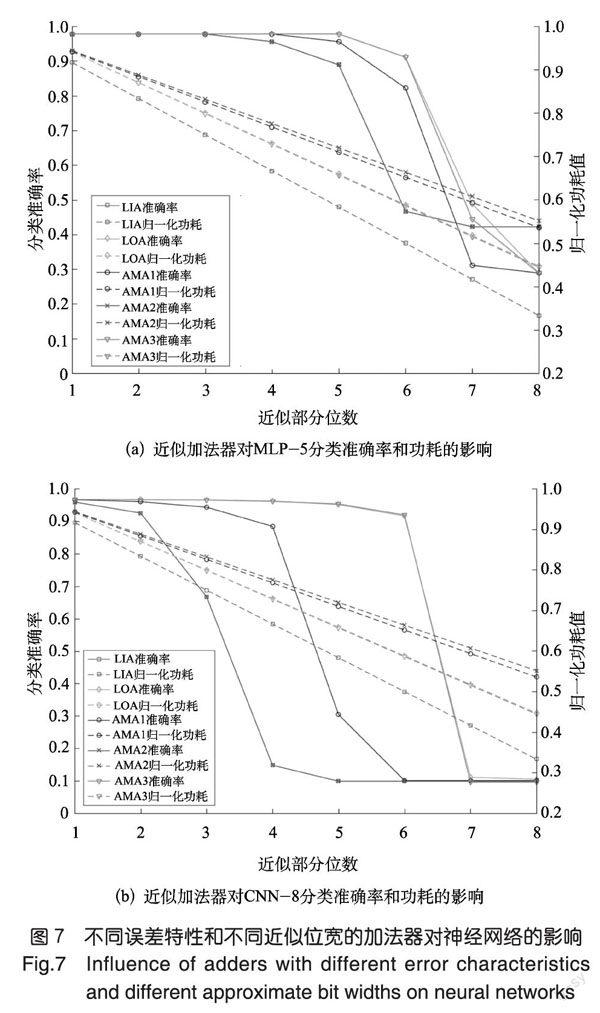
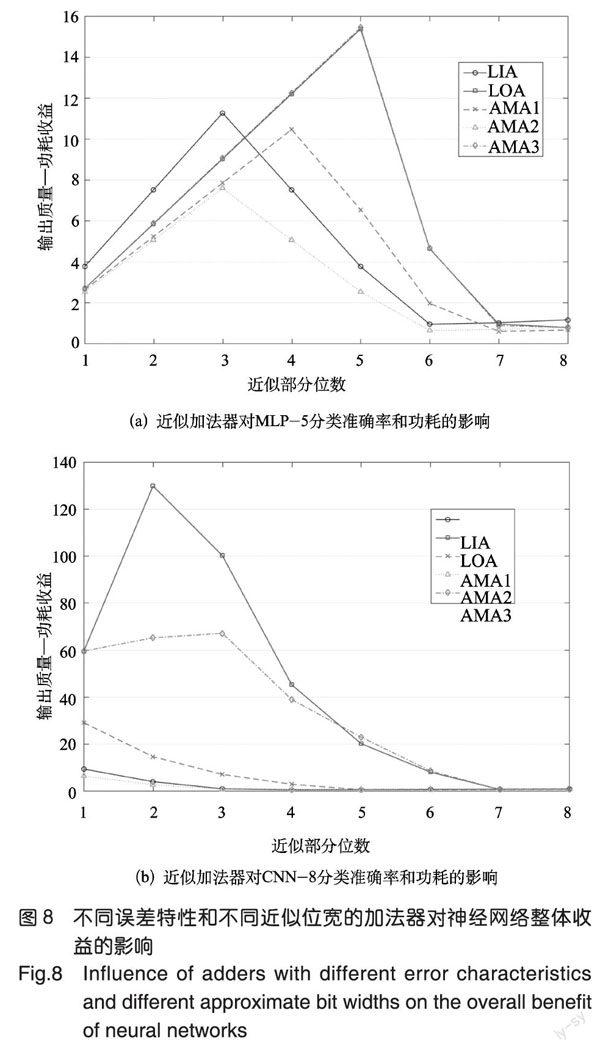
將本文提出的兩層結構多位近似加法器模型加入MLP-5和CNN-8中，探究不同誤差特性的近似加法器（LIA、LOA、AMAI、AMA2、AMA3）和不同近似位寬（1～8位）對4.2節神經網絡三個指標的影響，結果如圖7、圖8所示。

圖7中橫坐標均表示低位近似部分的位寬，實線表示分類準確率，虛線表示歸一化功耗。仿真發現，不同誤差特性的近似加法器對神經網絡分類準確率的影響差別很大，LOA和AMA3對網絡輸出質量影響最小，LIA和AMA2影響最大。試驗結果與誤差特性理論分析預測的結果是一致的，這表明，平均誤差越小的近似加法器對神經網絡的輸出質量影響越小，原因在于實際運算時誤差可以互相削弱甚至補償，誤差累積小，而傳統減少位寬的近似方法是最差的方案。其次，隨著近似位寬的增加，分類準確率不斷下降，且存在一個突變節點，當近似位寬大于閾值之后，分類準確率嚴重下降。不同近似加法器的近似閾值存在差別，在CNN-8網絡中，LOA、AMA3為6位，LIA和AMA2為2位。此外，歸一化加法計算功耗隨著近似位寬增加線性下降。特別地，當近似位寬位為閾值時，LOA和AMA3能減少約45%的加法計算功耗，而LIA只能減少約20%。

而從本文提出的整體收益角度看，計算出各種近似設計下的輸出質量一功耗收益，如圖8所示，橫坐標表示近似位寬，縱坐標表示輸出質量一功耗綜合收益數值，研究發現，LOA、AMA3為網絡帶來的輸出質量一功耗收益最高，LIA、AMA2的收益最低，且每種近似加法器都存在一個收益最高的近似位寬，輸出質量一功耗收益隨著近似位寬的增大先上升后下降，以MLP-5為例，采用LOA和AMA3近似5位時為網絡帶來的整體收益最高。采用這種方法可以很直觀地為不同應用找到最合適的近似加法器以及近似位寬。而通過改變輸出質量一功耗收益指標中的權重值，可以滿足不同應用對輸出質量、功耗的不同需求，實現不同應用的最優近似設計。5結論

本文提出了一套完整的面向神經網絡加速器的電路級近似計算單元的設計方法，通過對近似加法器進行誤差和功耗分析，為其在神經網絡的應用提供指導原則，通過搭建靈活性高的典型神經網絡框架和近似加法器的算法模型，解決了傳統網絡框架不便于進行近似處理的問題，研究了不同誤差特性和不同近似位寬的加法器對神經網絡的影響，研究表明，平均誤差小的近似加法器對神經網絡的輸出質量影響小，且存在近似位寬閾值，超過閾值會導致輸出質量驟降，近似加法器可以大幅降低加法計算功耗。而采用本文提出的輸出質量一功耗收益指標，可以直觀地在電路級別對不同應用進行最優設計。當然，本研究還存在一些不足，只對加法器進行了近似處理，但從表1看出神經網絡中乘法運算也占據很大比重，進一步對乘法器進行近似處理可以降低更多的計算功耗。此外，神經網絡內部各個神經元容錯性存在很大差異，充分利用差異對近似方法進行優化可以為神經網絡加速器帶來更高的收益。

參考文獻

[1]Gupta V，Mohapatra D，Raghunathan A，et al.Low-powerdigital signal processing using approximate adders[J].IEEETransactions on Computer-Aided Design of Integrated Circuitsand Systems，2013，32（1）：124-137.

[2]Yang T，Ukezono T，Sato T.A low-power yet high-speedconfigurable adder for approximate computing[C]//InternationalSymposium on Circuits and Systems，2018.

[3]Liu B，Dong W，Xu T，et al.E-ERA：An energy-efficientreconfigurable architecture for RNNs using dynamically adaptiveapproximate computing[J].Ieice Electronics Express，2017，14（15）：66-77.

[4]Ho N M，Manogaran E，Wong W F，et al.Efficient floatingpoint precision tuning for approximate computing[C]//DesignAutomation Conference.IEEE，2017：63-68.

[5]Venkatesan R，Agarwal A，Roy K，et al.MACACO：Modelingand analysis of circuits for approximate computing[C]//IEEE/ACM International Conference on Computer-Aided Design.IEEE，2011：667-673.

[6]Huynh T V Deep neural network accelerator based on FPGA[C]//Nafosted Conference on Information and Computer Science，2017：254-257.

[7]Mahdiani H R，Ahmadi A，Fakhraie S M，et al.Bio-inspired imprecise computational blocks for efficient VLSIimplementation of soft-computing applications[J].IEEETransactions on Circuits&Systems，2010，57（4）：850-862.

[8]Venkataramani S，Ranjan A，Roy K，et al.AxNN：energy-efficient neuromorphic systems using approximate computing[C]//Low Power Electronics and Design（ISLPED），2014.

[9]Gupta V，Mohapatra D，Sang P P，et al.IMPACT：Impreciseadders for low-power approximate computing[C]//Low PowerElectronics and Design.IEEE，2011：409-414.

[10]Liang J，Han J，Lombardi F.New metrics for the reliability ofapproximate and probabilistic adders[J].IEEE Transactions onComputers，2013，62（9）：1760-1771.