深井大斷面硐室穩定性控制技術研究*
喬富尚,李寶石,馬浩吉,王朝壘
(1. 山東黃金礦業(玲瓏)有限公司,山東 招遠 265400;2. 北京科技大學 土木與資源工程學院,北京 100083;3. 中礦資源勘探股份有限公司,北京 100089)
1 引言
隨著淺部資源的逐漸消耗,越來越多的礦山開始向深部開采進行過渡[1-2],而在深部開采中,會面臨高應力、高井深、高水壓和高溫等環境,對礦山的安全生產不利,使礦山的生產成本增加[3]。為了適應當前的深部開采環境,礦山的設備逐漸向大型化方向發展,這就要求井下建更多的大型硐室與之匹配[4-5]。常見的井下大型硐室主要包括配電硐室、水泵房和破碎硐室等,其服務年限長,對其安全穩定性要求較高[6-8],因此,需針對深井礦山中的大型硐室進行系統的研究,以保證礦山的安全生產。
針對深井大斷面硐室的穩定性問題,國內外學者對此進行了大量的研究,李會明[9]的研究表明影響深井大斷面硐室圍巖穩定性的主要因素為硐室的形狀、圍巖條件、服務年限和及其支護方案等;梁權宇[10]建立三維數值計算模型,對深井大斷面硐室的變形規律進行了研究;程燕學[11]提出了錨噴注的聯合支護方案,實現了對大斷面硐室圍巖穩定性的有效控制;針對某礦水泵房復雜的地質條件,曹栩[12]提出了立體式工字鋼桁架支護技術與注漿加固聯合技術,在該大斷面硐室的支護取得良好效果;LI Chong[13]將雙層拱支護技術應用于某礦深部大斷面硐室的支護中,表明雙拱協同支護作用可保證大斷面硐室的長期穩定性。這些研究成果揭示了深井大斷面硐室的破壞機理,對深井大斷面硐室圍巖的穩定性控制具有重要的借鑒意義,但不同礦區的大斷面硐室面臨不同的復雜地質條件,需針對不同地質條件的大型硐室提出與之相適應的支護方案。
為了解決深井大斷面硐室的穩定性問題,本文以某銅礦深井大斷面配電硐室為研究對象,在充分掌握該硐室工程地質情況的基礎上,提出“噴射混凝土+鋼網+錨桿+長錨索”的聯合支護方案,并采用數值模擬的手段對其穩定性進行驗證,為礦山進行安全生產提供指導。
2 工程地質情況
某銅礦位于非洲中部國家贊比亞,礦產資源豐富,該礦設計生產能力為330萬t/年,建設周期為5年。為了適應當前低迷的礦業環境,該礦朝著智能化礦山的方向發展,引用了山特維克等一系列的大型采礦設備,因此,井下的巷道和硐室均趨于大型化,中央配電硐室為礦山的重要工程,主要用于對整個礦區的井下生產提供電力,其穩定性對礦山的安全生產具有重大的意義。
通過在現場對該銅礦的配電硐室進行工程地質調查,配電硐室主要賦存在下盤石英巖中,其單軸抗壓強度和抗拉強度均較大(單軸抗壓強度和抗拉強度分別為102.5MPa和14.2MPa),硐室周邊較為干燥,地下水對其影響較小,但該硐室存在2~3組優勢節理面,其中有一組節理面對硐室兩幫的影響較大,這些節理將巖體劃分為一系列的巖塊,對硐室的穩定性不利。
3 大斷面硐室控制技術
某銅礦井下大型配電硐室寬度為8.9m,高度為5.3m,其中直墻段高度為3.3m,斷面形狀為三心拱斷面,在維護過程中受地下水、地應力等因素的影響,其穩定性制約因素較多,且配電硐室附近分布有水泵房、水倉等大型硐室,為了保證某銅礦深井大型硐室支護的經濟和安全性,某銅礦井下大斷面配電硐室在支護過程中,應結合現代礦山大型硐室支護理念,遵循以下幾個原則:(1)支護的及時性。(2)需考慮支護體與圍巖的共同作用。(3)控制原則。(4)易于施工且成本低。
綜合考慮上述幾點,再結合某銅礦主礦體和西礦體各類大型硐室的支護形式,決定采用“樹脂錨桿+鋼網+噴射混凝土+錨索”聯合支護方式對其進行支護,通過經驗公式法和理論計算法進行計算得到的配電硐室支護參數如下:
(1)金屬網。通過對該配電室的工程地質情況進行調查,發現局部存在破碎帶,因此,需采用金屬網對破碎帶區域進行支護。金屬網材料為A3鋼,鋼筋直徑為6mm,網格為100mm×100mm,網片尺寸為2400mm×1200mm,搭接長度不小于200mm。
(2)噴射混凝土。根據工程類比法,該硐室應噴射的混凝土厚度為50mm,結合沖切破壞作用和黏結破壞作用計算的噴層厚度,綜合分析認為某銅礦深井大斷面配電硐室的噴層厚度取為50mm,且混凝土等級為C25。
(3)錨桿。采用樹脂錨桿進行支護,施工位置為兩幫及拱頂,間排距為1000mm×1000mm,長度為2200mm,直徑為20mm。
(4)長錨索。該硐室加強支護采用5000mm長的錨索支護,錨索直徑為15.24mm,支護網度:間排距2000mm×2000mm,且錨索的方向應與巷道壁相互垂直。
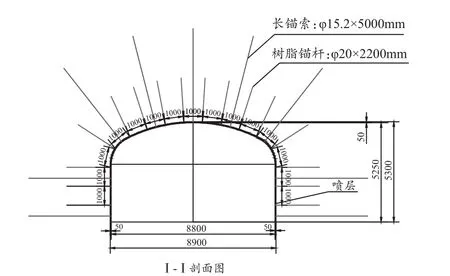
圖1 配電硐室支護剖面圖
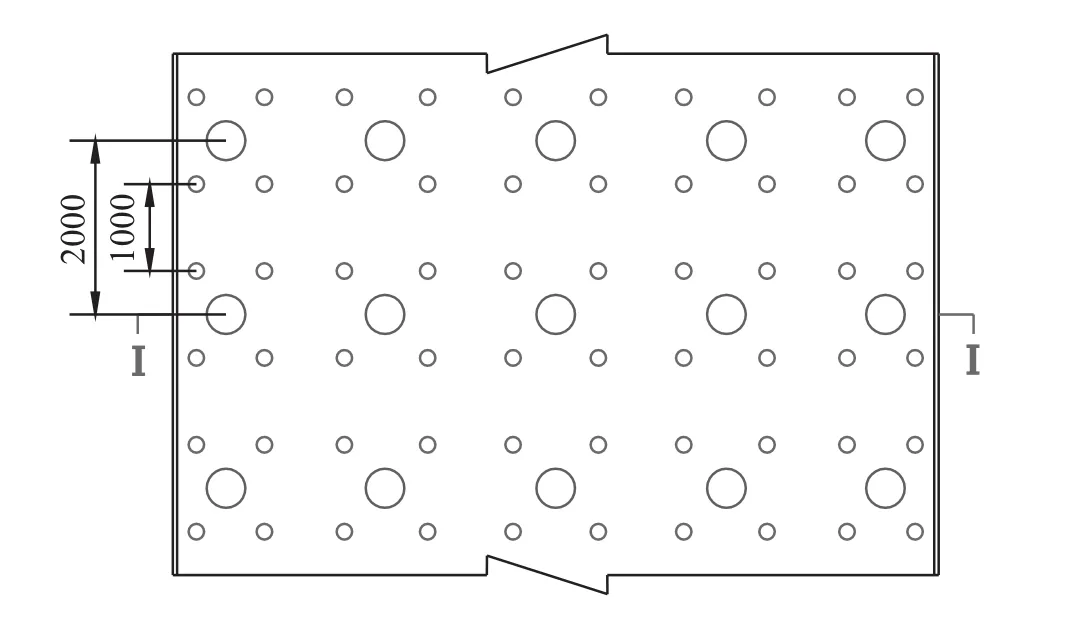
圖2 配電硐室錨桿和錨索分布圖
4 支護效果數值模擬分析
4.1 數值模型的建立
由于硐室的形狀為三心拱,FLAC-3D建立三心拱模型較為復雜,因此,本文采用CAD建立三心拱硐室模型,然后將其導入到ANSYS軟件中進行網格劃分,最后將其導入到有限差分軟件FLAC-3D軟件中進行計算,劃分好網格的模型如圖3所示。根據圣維南原理,硐室的開挖一般會對周圍3~5倍的巖體產生影響,而硐室的寬度為8.9m,高度為5.3m,因此整個模型的長度為80m,寬度為40m,高度為60m,其中沿X方向為長度方向,沿Y方向為寬度方向,沿Z方向為高度方向。為了提高計算機的計算效率,在網格劃分過程中,靠近巷道中心越近,網格劃分的越密集;距離巷道中心越遠,網格劃分的越稀疏,整個模型共劃分網格單元112000個,節點116481個。

圖3 數值計算模型
4.2 數值模擬方案的選擇
為了對比配電硐室在不支護情況和支護情況下的穩定性,需分別建立硐室模型,方案1對硐室不進行支護,方案2中對硐室采用“錨桿+錨索+錨網+噴射混凝土”聯合支護方式,如圖3所示為硐室在支護和不支護情況下的數值計算模型。整個模型的在計算過程中的開挖與支護步驟如下:
在一定程度上,軟件中用戶賬號需要與學生本人具有同等法律效力,特別在審批、簽到等環節。這是軟件能夠順利運行推廣的前提條件。因此,學院需要明確告知學生該賬號在學生管理工作中的重要性,提醒同學關注賬號安全并簽訂協議。
(1)計算硐室在原巖應力情況下的應力狀態。
(2)原巖應力狀態計算完成后,對整個模型的位移和速率清零,開始對硐室進行開挖2m。
(3)繼續開挖2m長的硐室,然后對不支護情況下的硐室不采取任何支護形式,對支護情況下的硐室采用“錨桿+錨索+錨網+噴射混凝土”聯合支護方式對上一段開挖的2m區域進行支護。
(4)再開挖2m,對不支護情況下的硐室不采取任何支護形式,對支護情況下的硐室采用“錨桿+錨索+錨網+噴射混凝土”聯合支護方式對上一段開挖的2m區域進行支護。
(5)重復步驟(4)中的過程,直至該配電硐室開挖完成。
4.3 邊界條件
配電硐室的頂部為上覆巖層,因此,在硐室的頂部施加應力邊界條件,所施加的應力大小為28.28MPa;模型的底部為固定邊界條件,設置其X、Y和Z方向的位移均為0;模型的前后左右四個面分別設置為位移邊界條件,其中前后兩個面分別設置為沿Y方向的位移為0,左右兩個面分別設置為沿X方向的位移為0。
4.4 巖體物理力學參數
通過在室內進行巖石力學試驗可得到巖石的物理力學參數,結合現場工程地質調查的結果,采用Hoek-Brown強度準則對其物理力學參數進行折減,得到巖體的物理力學參數如表1所示:

表1 某銅礦巖體物理力學參數
4.5 計算結果分析
分別按照上述步驟模擬某銅礦深部大型配電硐室在支護與不支護情況下的穩定性,主要從位移、應力和塑性區分布幾個方面對該配電硐室圍巖的穩定性進行分析。為了更加直觀地反映支護效果的好壞,通過在Y=20m的位置作一個剖面,來分析該剖面上的圍巖位移、應力和塑性區分布情況。
4.5.1 位移分析
如圖4和圖5所示為配電硐室在不支護和支護情況下的水平位移和豎直位移分布云圖,從圖中可以得到如下幾點結論:
(1)隨著硐室的開挖,應力得到釋放,圍巖發生變形,硐室的頂板圍巖發生下沉,底板圍巖出現底鼓現象,兩幫圍巖向硐室內側擠壓,發生片幫。
(2)對比在支護與不支護情況下硐室的豎直位移和水平位移的數值,不支護情況下,硐室頂板、兩幫及底板的最大變形量分別為11.95cm、8.45cm和12.81cm;硐室在進行支護后,硐室頂板、兩幫及底板的最大變形量分別為3.05cm、2.42cm和3.13cm。對比不支護與支護情況下硐室頂板、兩幫及底板變形情況,采取支護方式后,硐室的頂板、兩幫和底板的最大變形量分別減小74.47%、71.36%和75.57%。

圖4 配電硐室水平位移分布
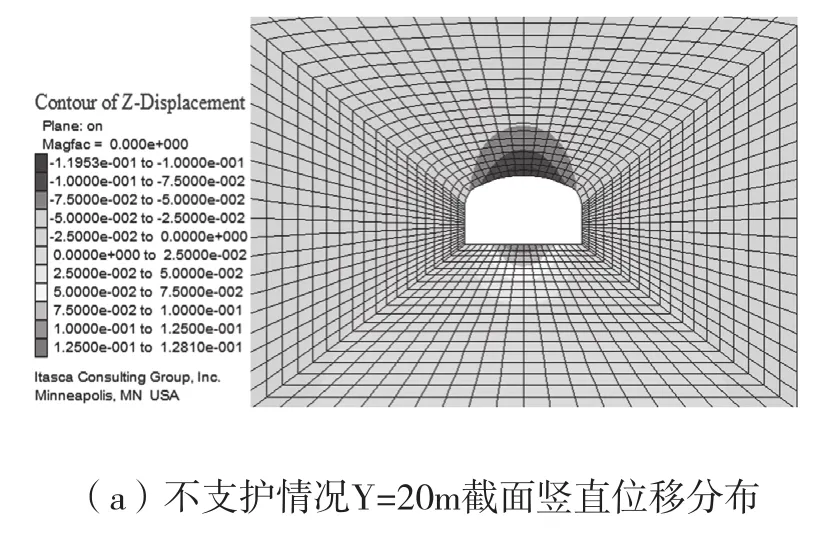

圖5 配電硐室豎直位移分布
4.5.2 應力分析
如圖6和圖7所示為某銅礦大型配電硐室在不支護與支護情況下的應力分布情況,在開挖之前,硐室處于原巖應力狀態,隨著硐室的開挖,硐室周圍的應力得到釋放,應力進行重分布,越靠近巷道中心,應力集中程度更大,越遠離巷道中心,應力越接近原巖應力狀態,這也與圣維南原理相符合,距離開挖區域越遠,硐室的開挖對其影響越小。
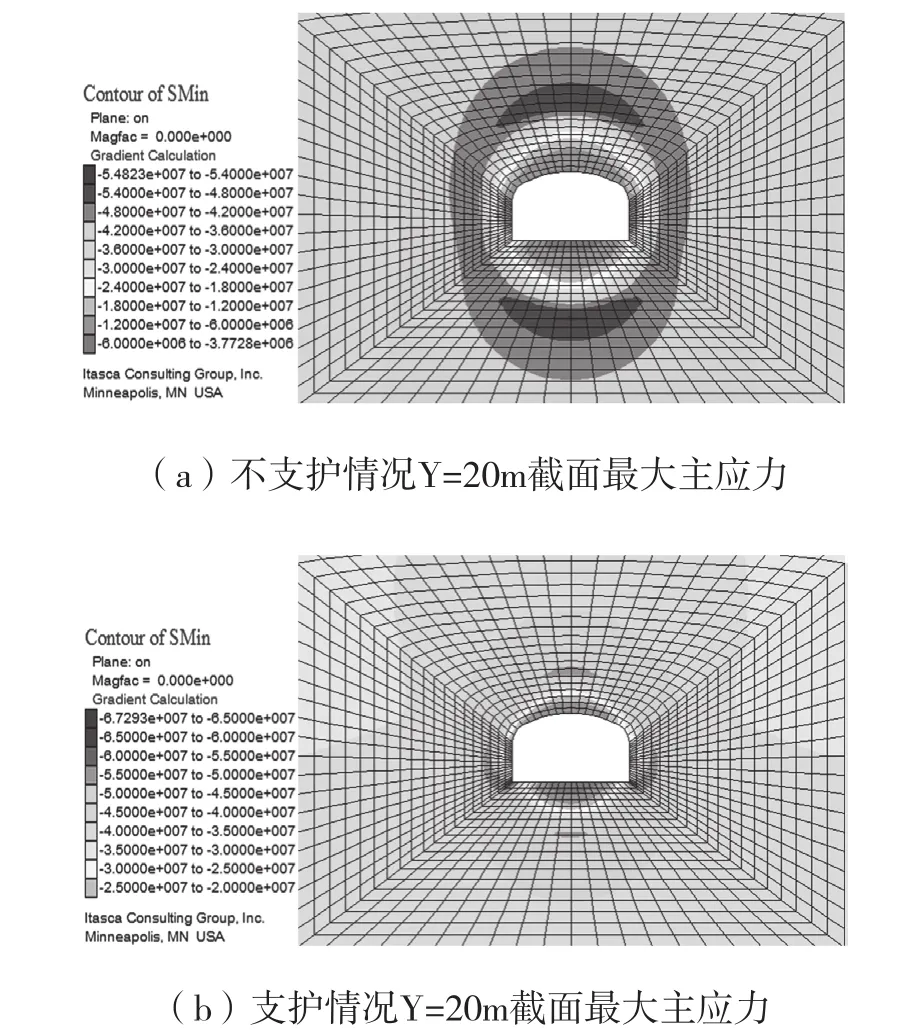
圖6 配電硐室最大主應力分布
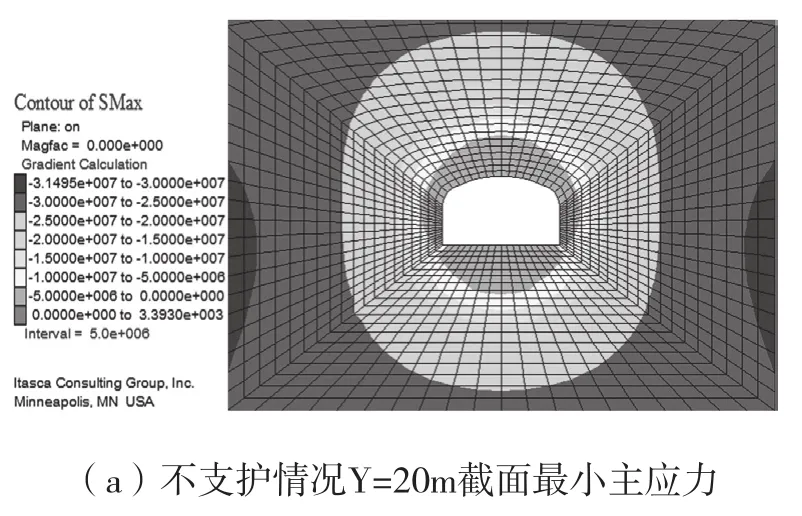
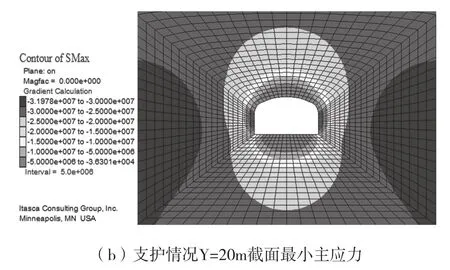
圖7 配電硐室最小主應力分布
不支護情況下硐室最大主應力值為54.18MPa,最小主應力為31.49MPa,且最大主應力近于水平方向,對硐室進行支護后,硐室的最大主應力為67.29MPa,比不支護情況還高;但在不支護情況下,硐室頂底板出現了0.0034MPa的拉應力,表明在采用支護方式后,對硐室的受力情況影響不大。
4.5.3 塑性區分析
如圖8所示為某銅礦大型配電硐室在不支護情況和支護情況下的塑性區分布情況,無論硐室是否進行支護,硐室兩幫的塑性區分布呈完全對稱分布,頂底板塑性區范圍也基本呈現對稱分布的規律。且剪切破壞主要發生在硐室的周邊及硐室內壁,而拉伸破壞主要發生在沿硐室壁的一層圍巖,遠離硐室壁只出現局部的拉伸破壞。
支護前,硐室的塑性區面積較大,硐室頂板、兩幫及底板的塑性區半徑分別為5.25m、2.34m和5.92m。對硐室進行支護后,硐室的頂板、兩幫及底板的塑性區半徑分別為2.84m、1.72m和3.99m。與不支護情況進行對比,硐室的頂板、兩幫及底板塑性區分別減小45.90%、26.49%和32.60%。這些都表明,在采用合理的支護形式后,硐室的穩定性得到有效控制,特別是硐室的頂板塑性區半徑明顯減小。

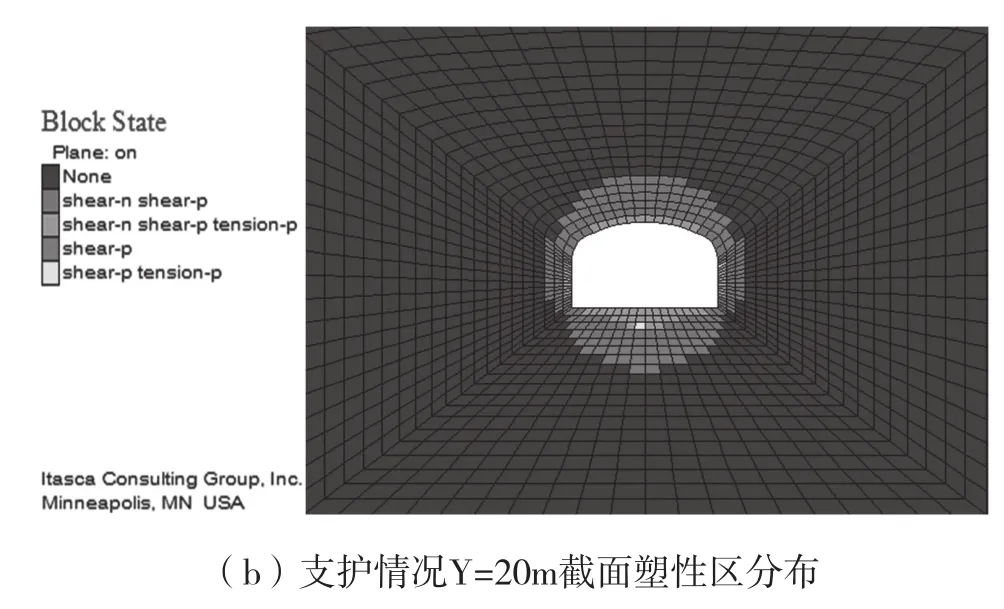
圖8 配電硐室塑性區分布
5 結論
(1)結合某銅礦大斷面配電硐室的服務年限及開采技術條件,結合現代礦山大型硐室支護的理念,并根據工程類比法和相關理論提出了該配電硐室支護的設計依據,提出了“噴射混凝土+鋼網+錨桿+長錨索”的聯合支護方案。
(2)根據經驗公式法和理論計算法對某銅礦大斷面配電硐室的支護參數進行了計算,確定噴射混凝土厚度為50mm;錨桿的支護參數為:采用樹脂錨桿,錨桿直徑為20mm,錨桿長度為2200mm,錨桿間排距為1000×1000mm;錨索的支護參數為:錨索直徑為15.24mm,錨索孔直徑為49mm,長度為5000mm,間排距為2000×2000mm,局部采用鋼網進行加強支護。
(3)數值模擬計算的結果表明,采用“樹脂錨桿+鋼網+噴射混凝土+錨索”聯合支護方式后,硐室的穩定性得到明顯改善,塑性區面積大大減小,硐室的變形量在可控制的范圍之內,能保證硐室的長期穩定性,可為類似工程進行合理支護設計提供一定的借鑒。

