聚焦數學思想的前行 推升學生的學習層次

張曉菊

（江蘇省海門市海門港新區實驗學校，江蘇海門 226156）

引 言

美國教育學家布魯納說過：“領會基本的數學思想和方法是通向遷移大道的光明之路”，可見數學思想在學生數學學習中的重要性。如果教師在教學中只注重基本知識的傳遞和基本技能的訓練，那么學生的數學學習就難以邁上新的臺階。

一、選擇合適的載體，推動學生接觸數學思想

數學思想依靠學生的感悟。在數學教學中，教師需要選擇合適的載體來推動學生領悟，讓學生在具體的問題中發現數學的本質規律，找到解決同一類問題的方法。這樣在體驗到這些方法的優勢之后，學生就會形成思維定式，用最經濟的方法去嘗試解決問題。

例如，在教學《長方形的周長》時，除了讓學生熟練掌握長方形的周長計算方法，還應為學生帶來不一樣的圖形。在嘗試計算圖1 中圖形的周長時，一些學生用12減3算出上面一條邊的長度，再用8減2算出右邊一條邊的長度，然后將6條邊的長度分別相加，算出圖形的周長。在交流算法時，很多學生認為他們的方法更簡單。觀看了學生的演示之后，筆者利用多媒體動畫向學生展示了移動圖中兩條短邊的過程，讓學生發現這個圖形的周長其實與長方形的周長完全相同，這樣一個簡單的動畫讓學生對計算這個圖形的周長有了新的認識。再布置學生計算圖2和圖3的周長時，學生的進步就顯而易見了。他們利用了解決圖1的方法，用計算長方形的周長的方法算出了兩個圖形的周長。結束這個環節時，學生對這個方法已經有了足夠的認識：這些圖形就是在原來長方形的角落上剪去一個小長方形，只要移動圖形中的幾條邊，可以將原來圖形的周長轉化為長方形的周長，然后利用長方形的周長公式來計算。

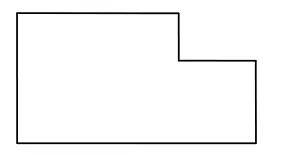
圖1

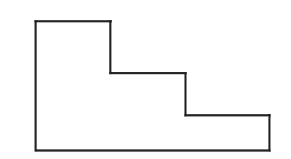
圖2

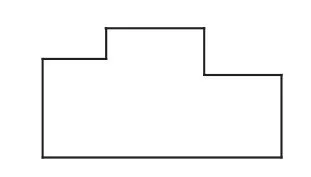
圖3

二、組織有效的交流，推動學生說出數學思想

數學思想不僅需要借助合適的載體來呈現，也需要讓學生嘗試說出自己的發現和領悟，用語言的形式來揭開數學思想的面紗，這樣可以讓學生更好地領悟數學思想。例如，在教學《圓的面積》之后開展的練習課，筆者挑選了這樣一個問題來讓學生獨立嘗試：如圖4所示 ，大正方形的面積是20平方分米，在正方形中有一個最大的圓，這個圓的面積是多少？在學生練習的時候筆者巡視了一圈，發現了一些有代表性的做法，于是在組織交流時有意挑選了一些學生的練習供大家討論。其中，有些學生用20÷4＝5，π×52＝25π來計算，很快有學生提出反對意見：這是將20當成正方形的周長了，現在已知的是正方形的面積。接著這個觀點，有學生提出質疑：正方形的面積是20平方分米是不是有問題，找不到一個數的平方等于20啊？在很多學生表示贊同時，有學生舉手發言：我們的確找不到一個數的平方等于20，但是我們根本不需要找到正方形的邊長啊，因為圓的面積等于π×r2，r2正好是大正方形面積的四分之一，所以只要用20÷5×π就可以算得圓的面積。可謂“一語點醒夢中人”。在這種思路的指引下，學生學會了圓的面積的計算方法。

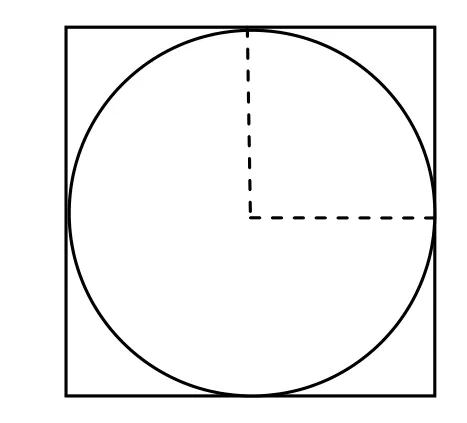
圖4

三、借助必要的反思，推動學生總結數學思想

在數學學習中，學生可能在有意無意間運用典型的數學思想解決過問題，不過因為他們對這樣的思想很陌生，所以學生可能在運用時沒有概念。但是這些經歷都是學生數學學習的寶貴財富，當積累到一定的階段時，教師就可以引導學生回顧反思，總結數學思想，推動數學思想的掌握[1]。

例如，在教學《轉化的策略》時，學生將例1中的兩個不規則圖形的面積轉化為規則的圖形面積來比較是非常正常的，而當時他們也只知道這樣來移動和拼接可以讓問題更簡單。但是在經歷了例2的學習之后，學生對轉化的思想就有了深刻的體會。他們發現有些按照常規思路來做會很復雜的問題，在利用轉化的策略之后就變得異常簡單，這讓他們深深地愛上了轉化的策略。建立在這樣的基礎上，筆者引導學生來回憶以往的數學學習中有沒有運用過這樣的方法來解決問題。學生很快回憶起在多邊形面積計算單元多次運用過轉化，如將平行四邊形的面積轉化為長方形的面積來計算，將三角形的面積和梯形的面積轉化為平行四邊形的面積來計算等，這些轉化都是將未知的問題轉化為已知的問題，用舊知識解決了新問題。還有的學生回憶起異分母分數的加減法，在計算時通過通分，將異分母分數轉化為同分母分數；在分數除法計算中，將除法轉化為乘法來計算。列舉了這么多實例之后，學生對于轉化策略的認識更加深刻。筆者借機指出：轉化不僅是一種解決問題的策略，更是我們在學習和生活中經常用到的一種思想，學生對轉化就有了更深一層的理解。

四、引導深入的思考，推動學生深化數學思想

數學思想是學生學習經驗的薈萃，也是學生知識素養的沉淀，它不同于一般性知識，可以告知；不同于一般的技能，可以刻意訓練，它更多地需要學生的領悟，當學生的認知達到一定高度時，他們會自然地將數學思想內化成自己的知識。為了推動學生的領悟，教師可以讓學生學以致用，多經歷，多嘗試，在廣泛的實踐和運用中深化數學思想[2]。

例：有這樣一個數學問題：不計算，比較24×26和25×25的大小，并說說你的想法。很多學生被“不計算”這個要求難住了，因為他們的第一反應就是通過計算來比較。在組織學生獨立思考和小組交流之后，有的小組的學生找到了方案：可以將兩個乘法算式看作計算一個長方形和一個正方形的面積，因為兩個算式中的乘數的和相等，就相當于這兩個圖形的周長相等，而周長相等時，長與寬越接近，面積就越大，所以25×25大于24×26。聽了學生的發言之后，筆者展示了學生畫的圖，并讓大家通過計算來驗證這個結論，大家對結果無異議。更為關鍵的是，學生從這個問題中發現了數形結合的妙處，這為他們萌生數、形結合的思想奠定了基礎。

結 語

讓學生在數學學習中積累方法和經驗并感悟數學思想，是教學的目標之一。在實際教學中，教師的著眼點不妨高一點，眼界不妨開闊一些，為學生創造更好的學習環境，讓他們多經歷探索和思考的過程，從而提煉和感悟數學思想，以此推動學生的深度學習。